濾波誤差攝動動態(tài)系統(tǒng)的無記憶狀態(tài)反饋控制器設計

吳 越

（吉林師范大學 數(shù)學學院，長春130000）

0 引言

不確定性時變時滯奇異攝動系統(tǒng)源于工業(yè)生產(chǎn)等控制領域中的應用，現(xiàn)在已經(jīng)成為現(xiàn)代控制科學的一個重要研究領域.關于系統(tǒng)的濾波器設計已有了比較詳盡的研究，例如，文獻［1］研究了含有不確定結構的時變時滯奇異攝動連續(xù)系統(tǒng)的濾波誤差動態(tài)系統(tǒng)的穩(wěn)定性分析問題，文獻［2］得到了連續(xù)系統(tǒng)的時滯依賴和時滯獨立兩種不同情形下的濾波誤差動態(tài)系統(tǒng)穩(wěn)定性的判別條件形式等等.在上述文獻中對連續(xù)系統(tǒng)的濾波誤差動態(tài)系統(tǒng)穩(wěn)定性分析問題的討論較為詳細，眾多學者對線性時滯控制系統(tǒng)中的濾波器設計問題展開了研究，取得了許多成果［3-4］，但并未涉及濾波誤差動態(tài)系統(tǒng)其他層面的研究.

本文運用線性矩陣不等式方法，主要對奇異攝動時滯濾波誤差動態(tài)系統(tǒng)的控制器設計問題進行研究，對帶有控制輸入的奇異攝動時滯濾波誤差動態(tài)系統(tǒng)，設計無記憶狀態(tài)反饋控制器［5］，借助于Lyapunov穩(wěn)定性理論和線性矩陣分析，構造一個新的Lyapunov 泛函，利用交叉項界定方法，推出控制器在時滯依賴和時滯獨立情況下的充分性判據(jù).

1 問題描述和引理

1.1 奇異攝動時滯濾波誤差動態(tài)系統(tǒng)概述

首先考慮帶有干擾輸入的不確定時變時滯奇異攝動控制系統(tǒng)

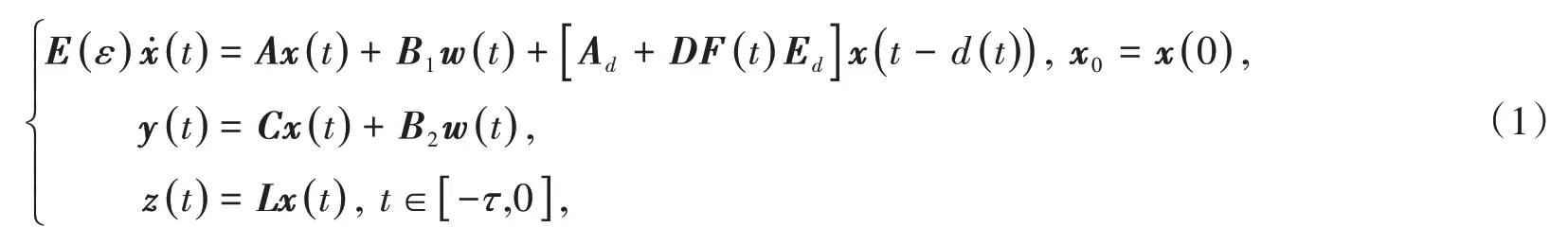
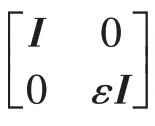
其中：τ，μ是已知實常數(shù)；F(t)∈Ri×j是范數(shù)有界的不確定系統(tǒng)模型參數(shù)矩陣，具有如下范數(shù)有界不確定性結構

在如下濾波器

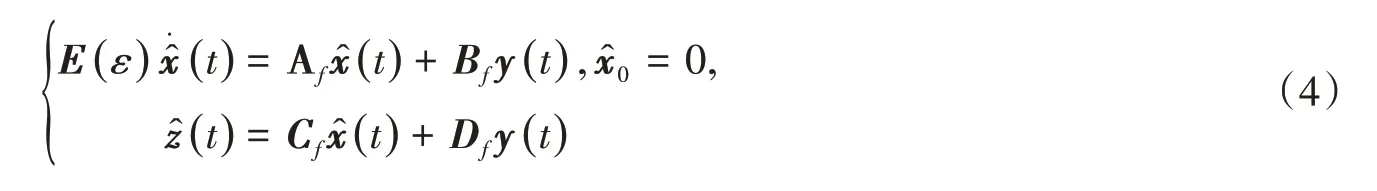
的作用下，形成如下濾波誤差動態(tài)方程為

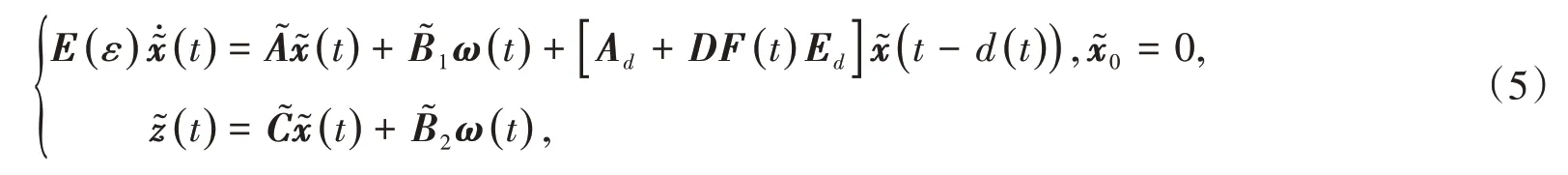
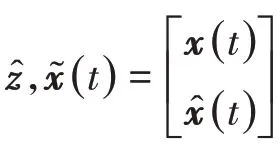
考慮帶有控制輸入和干擾輸入的奇異攝動時滯濾波誤差動態(tài)系統(tǒng)

其中：u(t)∈Rm是控制輸入向量；B是已知的適當維數(shù)的實常矩陣.

1.2 線性不等式理論及相關引理

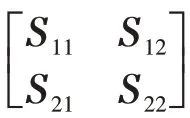
引理2［7］對于適當維數(shù)的矩陣E，D和對稱矩陣Y，若不確定矩陣F(t)滿足FT(t)F(t)≤I，則Y+EF(t)D+DTFT(t)ET＜0的充分必要條件是存在常數(shù)η＞0，使得Y+ηEET+η-1DTD＜0.

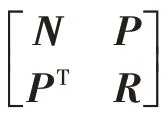
2 控制器設計

設計一個無記憶狀態(tài)反饋控制器

其中：K為未知的控制器增益矩陣.則閉環(huán)系統(tǒng)為

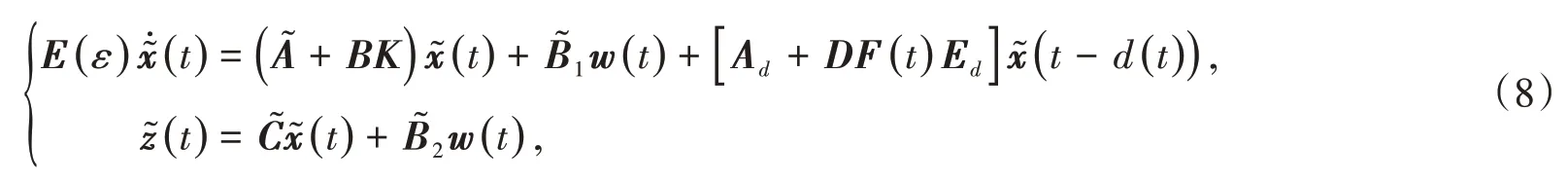
2.1 時滯依賴的控制器設計

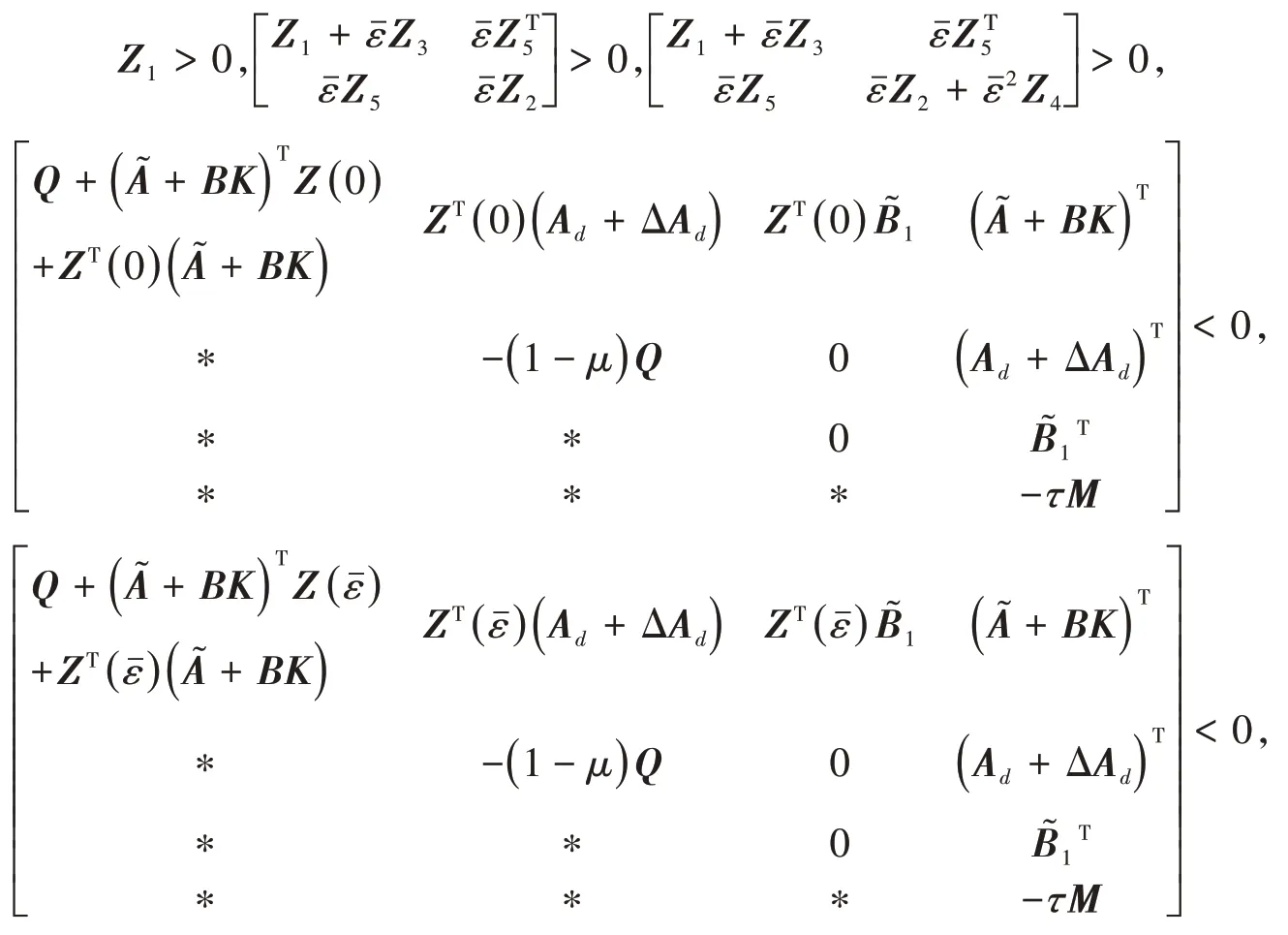
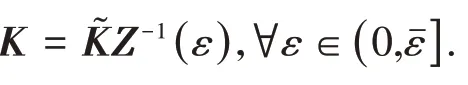
證明 構造函數(shù)V(x?(t))=V1(t)+V2(t)+V3(t)，

其中：

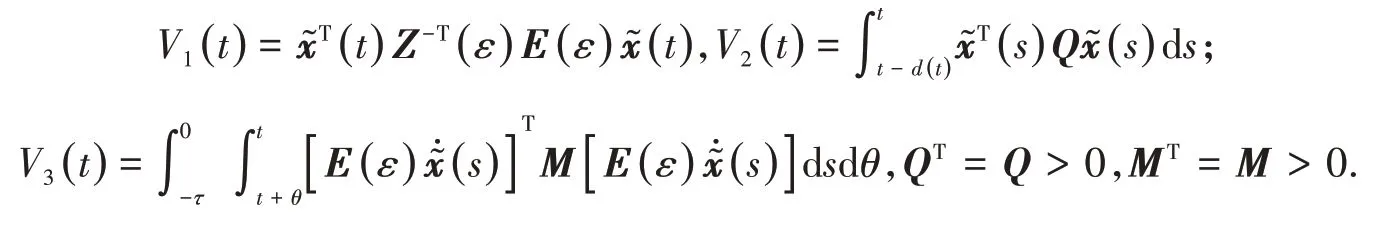
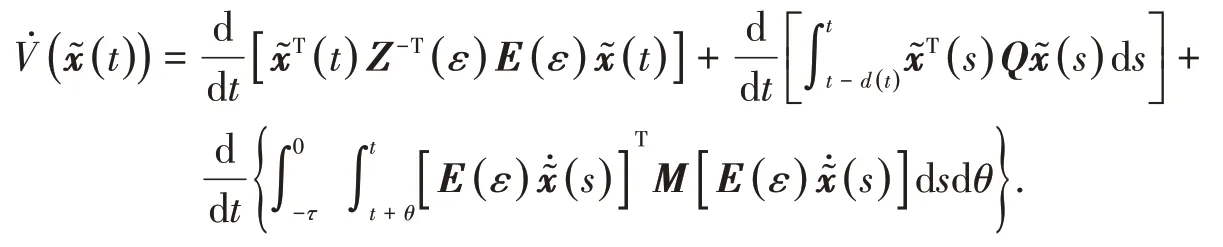
其中：

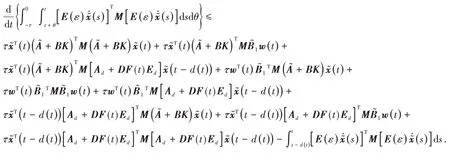
因此

其中：

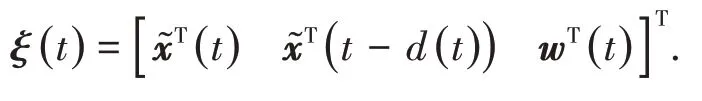
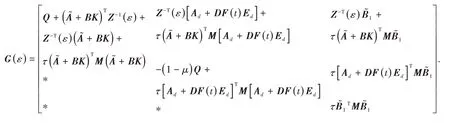
令ΔAd=DF(t)Ed，則由引理1，G(ε)＜0等價于

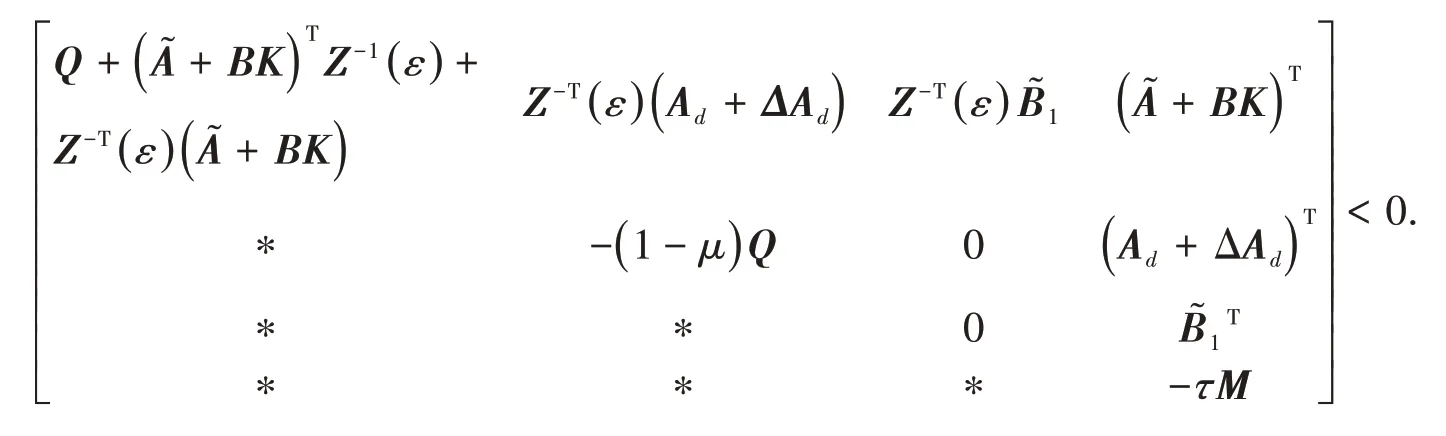
由線性矩陣不等式條件知，G( 0 )＜0，G()＜0.根據(jù)引理3，得G(ε)＜0，因此?((t))＜0，根據(jù)Lyapunov穩(wěn)定性理論，系統(tǒng)漸近穩(wěn)定.

為了求得控制器參數(shù)，需要去掉不確定函數(shù)F(t)，使得G(ε)＜0.對G(ε)＜0 左乘對角矩陣diag{ZT(ε)ZT(ε)ZT(ε)}，右乘其轉置，記KZ(ε)=?，再由引理1，存在一個常數(shù)γ＞0，得

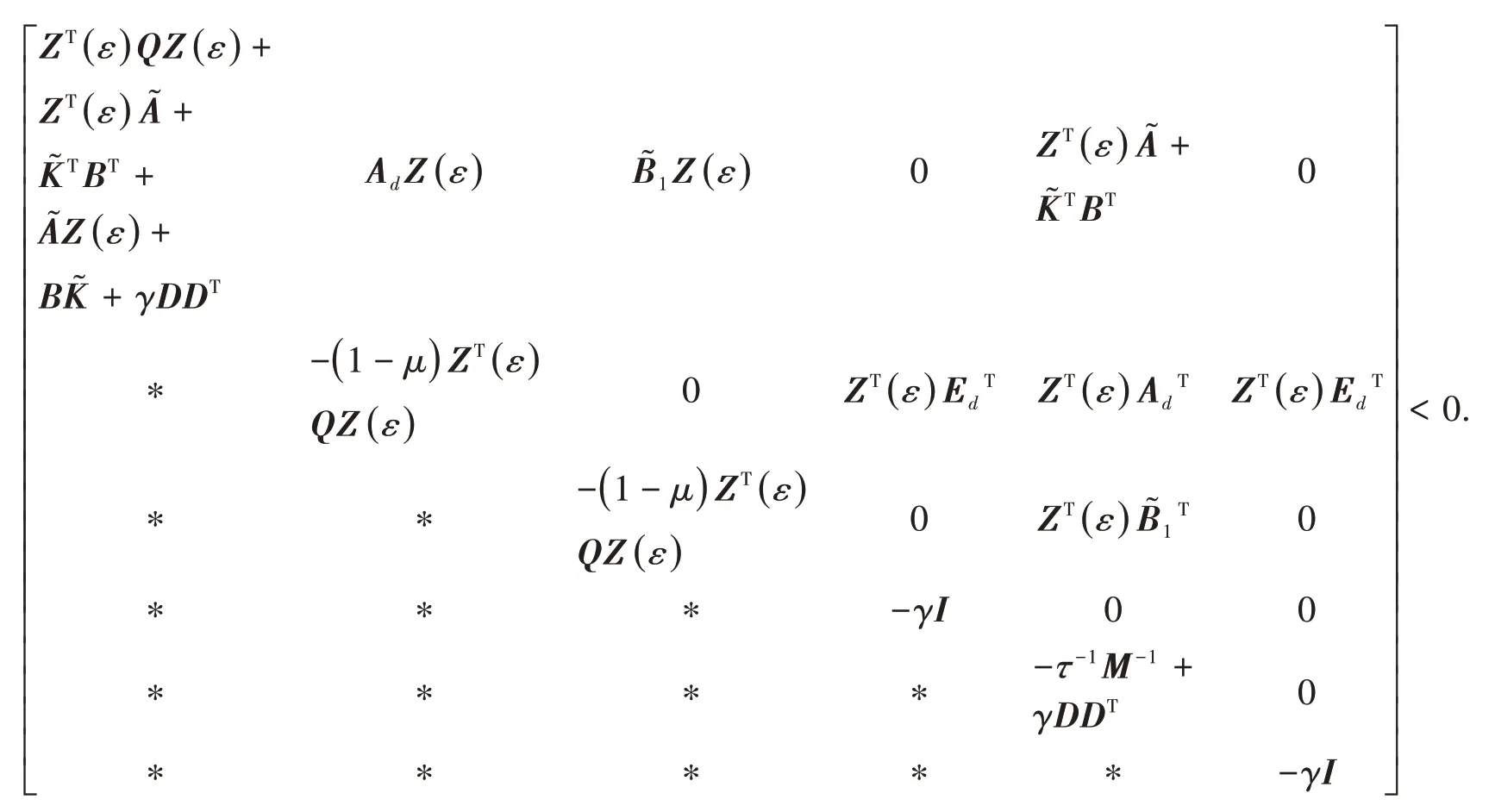
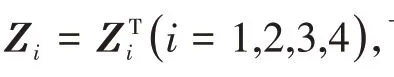
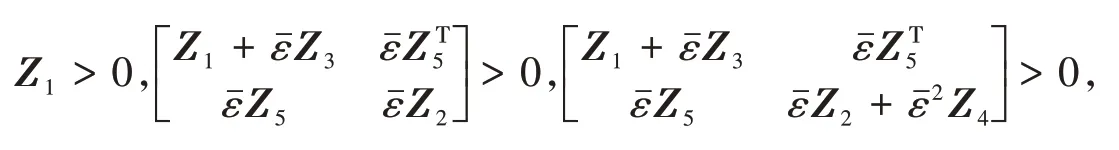
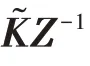
2.2 時滯獨立的控制器設計

定理3 給定＞0，濾波誤差動態(tài)系統(tǒng)對?ε∈( 0,)是漸近穩(wěn)定的.若存在對稱正定矩陣Q＞0，適當維數(shù)的矩陣P，對稱陣N，P，以及≥0，矩陣Zi(i= 1,2,3,4,5 )且Zi=(i= 1,2,3,4 )，使得不確定性函數(shù)滿足條件( 3 )，則下列矩陣不等式條件可行

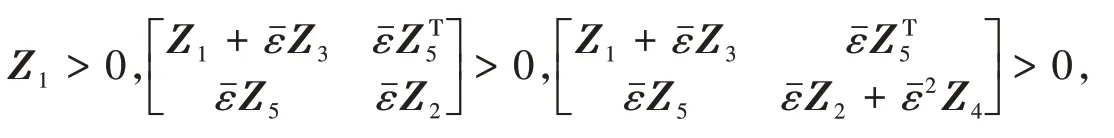
則u(t)=Kx(t)為系統(tǒng)( 6 )的靜態(tài)狀態(tài)反饋控制器，其中：K=?Z-1(ε)，?ε∈( 0,].

證明 構造函數(shù)V(x?(t))=V1(t)+V2(t)，

將V((t))沿著閉環(huán)系統(tǒng)的任意軌跡微分，得

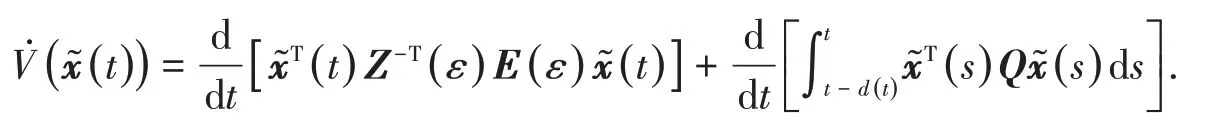
證明方法與定理1類似，故略.

定理4 給定＞0，濾波誤差動態(tài)系統(tǒng)對?ε∈( 0,)是漸近穩(wěn)定的.若存在對稱正定矩陣Q＞0，適當維數(shù)的矩陣P，對稱陣N，R以及≥0，γ＞0，矩陣Zi(i= 1,2,3,4,5 )且則下列矩陣不等式條件可行

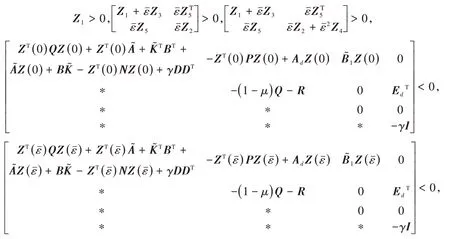
3 結論

本文對奇異攝動時滯濾波誤差動態(tài)系統(tǒng)進行無記憶狀態(tài)反饋控制器系統(tǒng)設計研究，構造適當?shù)腖yapunov泛函，使濾波誤差動態(tài)閉環(huán)系統(tǒng)漸近穩(wěn)定，推出時滯依賴和時滯獨立情形下的濾波誤差動態(tài)系統(tǒng)的控制器設計定理，該系統(tǒng)綜合性較高，盡可能減弱了時滯相關結論保守性的問題.