法拉第電磁感應定律的深度理解
劉麗
(云南省曲靖市羅平縣第一中學)
法拉第電磁感應定律定量反映了在磁通量變化時感應電動勢與穿過線圈磁通量變化率之間的數量關系.本文著重說明電磁感應電動勢與電源的電動勢之間的聯系,以及在具體物理情境的應用中要注意的問題.
1 對感生電動勢的理解
1.1 產生感生電動勢的非靜電力是感生電場對電荷的作用力
如果以E感表示感生電場強度,則沿任一閉合回路L的感生電動勢·dL.當磁場發生均勻變化時,產生的感生電場的電場強度的大小不變,其方向可以結合楞次定律確定.
例1如圖1所示,一絕緣圓槽固定在水平桌面上,槽中有一質量為m,帶電荷量為q的正電小球,槽的寬度遠小于其半徑r.將槽置于方向豎直向下的勻強磁場中,磁感應強度B隨時間變化的規律為B=kt(其中k保持不變),已知小球運動一周動能的增加量為Ek,求磁感應強度的變化率k.
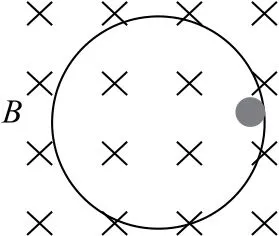
圖1
解析
由于槽中的磁場是均勻變化的,其產生的感生電場的電場強度大小不變.感生電場對帶電的小球的電場力使小球不斷加速,根據動能定理,電場力對小球做功,使得小球的動能增大,設感生電場強度為E感,根據動能定理有qE感·2πr=Ek,又因為槽內產生的感應電動勢為

1.2 感生電動勢的瞬時值與平均值的理解
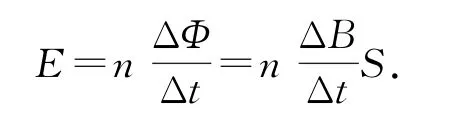
例2如圖2-甲所示,匝數為n、面積為S、電阻不計的導線圈與阻值為R的定值電阻相連,構成閉合回路.已知垂直穿過線圈的磁感應強度B隨時間t變化的規律如圖2-乙,以豎直向上方向為磁感應強度的正方向,求t=t0時刻電阻R上的電流大小.
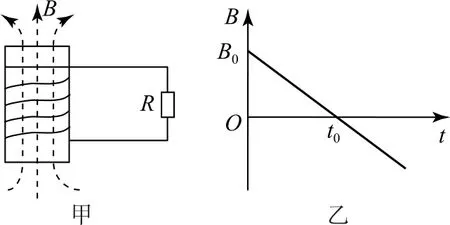
圖2
解析
由于穿過線圈的磁通量隨時間均勻變化,線圈中產生的感應電動勢是恒定不變的,所以t=t0時刻的感應電動勢等于0~t0時間內的平均電動勢,電動勢.根據閉合電路歐姆定律可知,電阻R上電流大小
2 對動生電動勢的理解
2.1 產生動生電動勢的非靜電力是磁場對運動電荷的作用力——洛倫茲力
如圖3所示,導體棒AC在勻強磁場中以速度u向上運動,導體中的自由電子隨導體一起以速度u運動,受到水平向左的洛倫茲力作用,形成由C指向A的附加電場,當附加電場對電子的作用力與其受到的洛倫茲力平衡時,導體兩端的電勢差保持不變.因此電子受到沿導體方向的洛倫茲力相當于電源中的非靜電力.掌握這一點對于解決磁流體發電、電磁流量計、霍爾效應的相關問題有很大的幫助.

圖3
2.2 對動生電動勢E=Blv 中速度的理解
導體棒平動切割磁感線時,v是導體棒與磁場間相對運動的速度.教材中推導動生電動勢的公式E=Blv時,是在假設磁場不運動,閉合回路的一部分導體在磁場中沿垂直磁場方向平動的情形下進行的.在實際生產和生活中,導體棒不運動(相對于地球)而磁場運動,或者磁場與導體均運動的情況并不少見,此時速度v應該理解為導體相對于磁場的速度.需要注意的是,當磁場“切割”導體,應用右手定則判斷感應電流方向時,大拇指的指向與磁場的運動方向相反.旋轉磁極式發電機工作時,就是磁極轉動,線圈不動,此時計算線圈中的感應電動勢,線圈相對于磁極的速度大小等于磁極旋轉的速度大小.磁懸浮列車則是利用列車底端的線圈移動的速度小于軌道區域內磁場移動的速度,此時線圈中感應電流受到的安培力與線圈和磁場之間的相對運動的速度方向相反,從而獲得向前運動的驅動力.
閉合回路中的雙金屬桿在勻強磁場中切割磁感線時,速度v是兩金屬桿切割磁感線運動的相對速度.
理論推導如圖4所示,兩條相距d的平行金屬導軌固定在水平桌面上,導軌平面有豎直向上的勻強磁場,磁感應強度的大小為B.垂直導軌放置兩長度均為d的金屬棒Ⅰ、Ⅱ,兩金屬棒沿導軌水平運動,若金屬棒Ⅰ運動的速度大小為v1,金屬棒Ⅱ運動的速度大小為v2,兩速度方向相同,且v1>v2,證明:回路中的電動勢E=Bd(v1-v2).

圖4
證明經過時間Δt,金屬棒Ⅰ向前運動的距離為x1=v1Δt,金屬棒Ⅱ向前運動的距離為x2=v2Δt,閉合回路的磁通量的變化量為
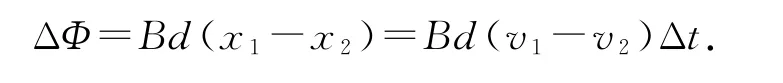
很顯然,若v1=v2,盡管兩金屬棒均做切割磁感線運動,但圍成的閉合回路的磁通量不變,所以,閉合回路中的總電動勢為零.同理,可以證明,若兩金屬棒的速度v1和v2的方向相反,則感應電動勢為
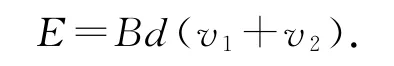
例3如圖5所示,在兩條足夠長相距為d的固定的光滑平行金屬導軌上垂直放置兩金屬桿MN、PQ,已知兩金屬桿的長度均為d,桿MN質量為m1、電阻為R1,桿PQ質量為m2、電阻為R2.金屬導軌處在磁感應強度為B、方向豎直向下的勻強磁場中.若MN桿受到水平向右的恒定的拉力F作用由靜止開始運動,求最終穩定時,兩金屬桿的速度差Δv的大小.

圖5
解析
金屬桿MN在恒力F作用下由靜止開始運動,回路中的感應電動勢與兩桿的速度差成正比,兩桿受到的安培力與兩桿的速度差成正比.所以金屬桿MN運動的加速度是逐漸減小的,而金屬桿PQ則是做加速度增大的變加速運動.當兩者速度的變化率相同時,相同時間內速度的增量相同.最終穩定時,回路的感應電動勢E=BdΔv,金屬桿中的感應電流,根據安培力公式,金屬桿受到的安培力大小均為f=BId,對金屬桿MN、PQ整體,根據牛頓第二定律,共同運動的加速度,隔離金屬桿PQ,有f=m2a,從而解得
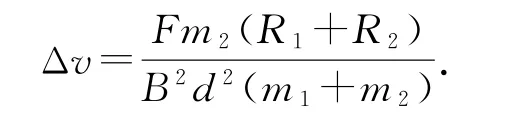
要形成正確的物理觀念,離不開對物理概念、物理規律的正確理解.只有深刻理解法拉第電磁感應定律的內涵,才能將其正確應用于解決實際問題之中.
(完)

