基于圖形構(gòu)建的“一題多解”探究與思考

李鴻飛

摘 要 “多解探究”培養(yǎng)學(xué)生思維寬度，能夠彌補(bǔ)學(xué)生單一的思維方式和解題方法，開拓學(xué)生視野，提升學(xué)生的解題效率;能促進(jìn)學(xué)生對同一問題從更深層次進(jìn)行思考，鞏固之前所學(xué)內(nèi)容并對其開拓創(chuàng)造。以蘇科版八年級幾何為例，從不同角度進(jìn)行圖形構(gòu)建，分析和探討“一題多解”對于提高學(xué)生數(shù)學(xué)素養(yǎng)的作用。

關(guān)鍵詞 中學(xué)數(shù)學(xué) 一題多解 圖形構(gòu)建

在數(shù)學(xué)教學(xué)中，一題多解探究可以培養(yǎng)學(xué)生發(fā)散思維，多角度看問題，多方位處理問題的能力。通過多解探究的練習(xí)能夠溝通新舊知識之間的聯(lián)系，提高學(xué)生應(yīng)用所學(xué)基礎(chǔ)知識和基本技能解決實(shí)際問題的能力，從而加深對所學(xué)知識的理解，開拓解題視野，提升解題效率。下面，筆者通過一道八年級幾何證明題，通過圖形構(gòu)建的多種證法來說明“一題多解”對學(xué)生數(shù)學(xué)核心素養(yǎng)培養(yǎng)的重要作用。

題目：如圖1，△ABC中，∠BAC = 90°，AB = AC，直線CD∥BA。動(dòng)點(diǎn)P是線段BC上的一點(diǎn)（靠近點(diǎn)C的一點(diǎn)），連接AP，過點(diǎn)P作PE⊥AP交直線CD于E。試探究PA與PE的關(guān)系。

分析：本題給出的條件有四個(gè)：一是∠BAC = 90°，二是AB = AC，三是CD∥BA，四是PE⊥AP。從本題可以看出，通過已知條件很難找到與所求之間的關(guān)系，這時(shí)我們就要通過作輔助線來解答[1]。對于同一個(gè)問題，不管如何選擇輔助線，都要先對已知條件和結(jié)論進(jìn)行分析。要證明PA = PE，有三種解題思路：（1）只要證明這兩條線段所在的兩個(gè)三角形全等，然后利用全等三角形的性質(zhì)證得PA = PE;（2）可以找出第三條線段，使得PA（或者PE）線段長度都等于這條線段長，最后利用等量代換證得PA = PE;（3）可以把這兩條線段放在同一個(gè)三角形中，利用等腰三角線的判定定理證得PA = PE。筆者在實(shí)際教學(xué)中，通過以下幾個(gè)方面，對此題進(jìn)行研究，給出如下不同的解法。

一、巧用截取構(gòu)建圖形

分析：對于學(xué)生來講，一般情況下，要證明兩條線段相等，只要證明這兩條線段所在的兩個(gè)三角形全等，然后利用全等三角形全等性質(zhì)，來證得PA = PE。那么如何才能構(gòu)造兩個(gè)全等三角形，這就需要教師引導(dǎo)學(xué)生從題目的已知條件和結(jié)論入手，展開想象、大膽嘗試，在對題目條件和圖形有一個(gè)整體的把握后，截取并構(gòu)造兩個(gè)全等三角形。

證法1：如圖2，在直線CD上取一點(diǎn)Q，使得PQ = PE，連接PQ。

因?yàn)椤螧AC = 90，AB∥CD。所以∠BAC = ∠ACD = 90°。因?yàn)锳P⊥PE，所以∠APE = ∠ACD = 90°。因?yàn)椤螦FP = ∠CFE，所以∠PAC = ∠PEC。而PQ = PE，所以∠PQE = ∠PEC，所以∠PAC = ∠PQE。又因?yàn)椤螧AC = 90°，AB = AC，∠ACD = 90°。所以∠ACB = ∠ABC = ∠PCQ = 45°。PC = PC，易證△CPA ≌ △CPQ，所以PA = PQ，因?yàn)镻Q = PE，所以PA = PF。

除證法1的截取方法外，還有另外兩種截取方法。證法2：如圖3，延長射線AC，在射線AC上取點(diǎn)Q，使得PQ = PA，連接PQ，易證△PCE ≌ △PCQ，所以PQ = PE，因?yàn)镻Q = PA，所以PA = PE。證法3：如圖4，過點(diǎn)P作PH⊥BC交AC與點(diǎn)H，只需要證△APH ≌ △EPC，所以PA = PE。

以上三種證法都使用了巧妙的截取。什么時(shí)候才能想到截取？當(dāng)題設(shè)中無法直接證明所要求的結(jié)論時(shí)，就要尋找第三變量，利用“轉(zhuǎn)化”的數(shù)學(xué)思想方法，從而化繁為簡、化難為易、化未知為已知。

二、善用對稱平行構(gòu)建圖形

分析：從圖形和已知條件中，可以看出∠ACB = ∠BCN（圖5）可能是對稱的，這就可以讓學(xué)生們聯(lián)想猜測BC可能是∠ACN的角平分線，然后利用角平分線這個(gè)特殊圖形及其性質(zhì)解決問題。

證法4：如圖5，過點(diǎn)P作PM⊥AC，PN⊥CD，垂足分別為M，N。

因?yàn)椤螧AC = 90°，AB∥CD。所以∠BAC = ∠ACD = 90°。因?yàn)锳P⊥PE，所以∠APE = ∠ACD = 90°。因?yàn)椤螦FP = ∠CFE，所以∠PAC = ∠PEC。又因?yàn)椤螧AC = 90°，AB = AC，∠ACD = 90°。所以∠ACB = ∠ABC = ∠BCN = 45°。所以CB是∠ACN的角平分線，因?yàn)镻M⊥AC，PN⊥CD，所以PM = PN，∠PMA = ∠PNC = 90°。易證△PMA ≌ △PNE，所以PA = PE。

同理，還可以過點(diǎn)B作BQ⊥CD，連接PQ（如圖6），證明方法同證法4。

對稱性是數(shù)學(xué)美的最重要特征，幾何中的對稱軸、中心對稱以及在代數(shù)中的許多運(yùn)用都能給人以美感。本題中以直線BC為對稱軸，由此想到了正方形這個(gè)基本模型和角平分線的性質(zhì)。以此為突破，從而很快解決了這個(gè)問題。所以，時(shí)刻要把數(shù)學(xué)的對稱美貫穿在學(xué)習(xí)中。由對稱性聯(lián)想到利用構(gòu)造平行線的方法，由此得到證法6和證法7。

證法6：如圖7，過點(diǎn)P作AB的平行線交AC于點(diǎn)M，過點(diǎn)E作EN⊥PM，垂足為N。可證出四邊形MCEN為矩形，所以NE = MC。易證得△AMP ≌ △PNE，所以PA = PE。

證法7：如圖8，過點(diǎn)P作PM∥AC交線段AB和直線CD于點(diǎn)M，N。可證出四邊形AMNC為矩形，所以AM = NC。易證得△PAM ≌ △EPN所以PA = PE。

構(gòu)造平行線探究基本規(guī)律，這是數(shù)學(xué)中常見的思維方法，本題中要證明PA = PE，就要把這兩條線段分別放在兩個(gè)特殊的直角三角形中。

三、利用旋轉(zhuǎn)構(gòu)建圖形

分析：通過類比構(gòu)造平行線的方法，我們也可以想到構(gòu)造平行四邊形這個(gè)特殊的模型來解決這個(gè)問題。根據(jù)題目中的條件可以巧妙地構(gòu)造之前學(xué)過的平行四邊形，基于平行四邊形模型，可以將△EPC圍繞某個(gè)點(diǎn)進(jìn)行不同的旋轉(zhuǎn)，從而解決這個(gè)問題。

證法8：如圖9，過點(diǎn)A作AM⊥BC，并延長AM，過點(diǎn)P作PN∥CD交AM的延長線于點(diǎn)N，連接CN。因?yàn)锳B = AC，∠BAC = 90°，AM⊥BC。所以AM = MC = MB，∠B = ∠ACB = 45°。因?yàn)锳B∥CD，CD∥NP，所以NP∥AB∥CD，所以∠B = ∠MPN = 45°。因?yàn)锳M⊥BC，所以∠PMN = 90°，所以∠MPN = ∠MNP = 45°，所以MN = MP，所以△AMP ≌ △CMN，所以PA = NC，∠PAM = ∠MCN。又因?yàn)镻A⊥PE，AM⊥BC，所以∠PAM+∠APM = ∠APM+∠EPC，所以∠PAM = ∠EPC，因?yàn)椤螾AM = ∠MCN，所以∠EPC = ∠MCN，所以PE∥NC，因?yàn)镻N∥CE，所以四邊形PNCE為平行四邊形，所以PE = NC，而NC = PA，所以PA = PE。

同理，過點(diǎn)C作CN⊥PC，使得CN = PC，過點(diǎn)N作NM∥PA交AC于點(diǎn)M，連接PN，如圖10，可得證法9，證法同證法8。

因此，在解決問題時(shí)我們要思考解法與解法之間的聯(lián)系與區(qū)別，要能夠觸類旁通。所以在解決數(shù)學(xué)問題時(shí)，我們往往會想到用類比的數(shù)學(xué)思想方法。由平行可以巧妙地構(gòu)造“特殊形”，即學(xué)過的平行四邊形，通過平行四邊形的性質(zhì)來解決這個(gè)問題。

四、構(gòu)造輔助圓構(gòu)建圖形

分析：借助等腰三角線的性質(zhì)來解決這個(gè)問題，由PE⊥AP會想到直角，由直角會想到構(gòu)造輔助圓來解決問題，由此可以借助初三圓的知識點(diǎn)來解決這個(gè)問題相對比較簡單。

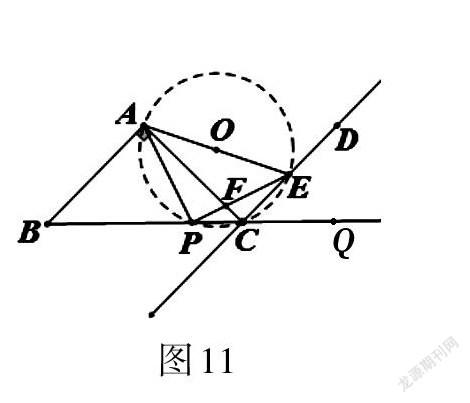
證法10：如圖11，在BC延長線上取點(diǎn)Q，連接AE。取AE的中點(diǎn)O，以O(shè)為圓心，OA為半徑畫圓。因?yàn)椤螧AC = 90°，AB = AC，所以∠ACB = ∠ABC = 45°。所以∠AEP = ∠ACB = 45°。因?yàn)椤螧AC = 90°，AB∥CD。所以∠BAC = ∠ACD = 90°。所以∠ECQ = ∠ACB = 45°。因?yàn)樗倪呅蜛PCE內(nèi)接于圓內(nèi)，所以∠ECQ = ∠PAE = 45°。即∠PAE = ∠AEP = 45°，所以PA = PE。

怎么會想到用構(gòu)造輔助圓來解決問題的呢？這就要求學(xué)生對圓的知識要足夠的了解，特別是怎樣才能確定圓。（1）不在同一條直線上的三點(diǎn)可以確定一個(gè)圓;（2）直角三角形也能確定一個(gè)圓;（3）當(dāng)一個(gè)圖形的一個(gè)角和角所對的邊確定時(shí)，也能確定圓（即定角定弦隱圓）。那么，本題應(yīng)是定角定弦隱圓的情況。

五、總結(jié)與反思

數(shù)學(xué)是思維的體現(xiàn)，怎樣才能培養(yǎng)學(xué)生的數(shù)學(xué)思維能力，這是數(shù)學(xué)教學(xué)過程中所要認(rèn)真思考的問題。通過“一題多解”，“多解歸一”的學(xué)習(xí)能培養(yǎng)學(xué)生思維的靈活性[2]，能夠激發(fā)學(xué)生的創(chuàng)造力，可以加深學(xué)生對所學(xué)知識的理解，訓(xùn)練學(xué)生數(shù)學(xué)方法的運(yùn)用，可以使學(xué)生對之前所涉及的知識進(jìn)行分析、歸納、總結(jié)，從而提高運(yùn)用知識的能力和解題的能力，解題的視野得到開拓、解題的效率得到提升，從而提升學(xué)生的數(shù)學(xué)綜合能力。為培養(yǎng)學(xué)生“一題多解”的能力，要注意以下幾個(gè)問題：

1.引導(dǎo)學(xué)生建立基本的模型，培養(yǎng)解題能力。教師在平時(shí)教學(xué)時(shí)引導(dǎo)學(xué)生總結(jié)出一些常見的幾何基本模型，并能夠運(yùn)用基本模型解題。平時(shí)注重基本模型的積累，積累的越多，越有助于激發(fā)學(xué)生提高解題的能力，有助于培養(yǎng)學(xué)生的創(chuàng)新意識。

2.引導(dǎo)學(xué)生注重解法類比，提高解題效率。在數(shù)學(xué)解題過程中，類比推理的方法可以解決很多類似問題，能夠找到同類問題的思路，讓問題更加清晰，讓復(fù)雜的問題簡單化，讓隱含性的問題更加顯性化。在初中教學(xué)中大膽使用類比方法，能夠提高學(xué)生的解題效率。

[參 考 文 獻(xiàn)]

[1]陳紅偉.一題多解練思維多解歸一探本質(zhì)[J].中學(xué)數(shù)學(xué)教學(xué)參考，2019（30）：31-32.

[2]金敏，王紅兵.立足核心素養(yǎng)彰顯思維品質(zhì)[J].中學(xué)數(shù)學(xué)教學(xué)參考，2019（32）：30-32.

（責(zé)任編輯：楊紅波）