基于序列信息的酶的亞類多特征參數識別方法

王 婷

(長治職業技術學院 山西長治 046000)

0 引 言

酶是人體健康的源泉，它幾乎參與所有的生命活動，如消化、呼吸、睡眠、思考、情緒、內分泌等。人體的生長和延續需要成千上萬種以上的酶化反應來實現。根據酶所能催化反應種類的不同，將酶分為6個家族類：氧化還原酶、轉移酶、水解酶、裂合酶、異構酶和合成酶[1-2]。按照國際科學文獻中的分類原則，在這6個家族類的基礎上，再根據底物中被作用的基團或鍵的特點進一步將每個家族分為不同的亞類[3]。酶的結構及作用機理與其所屬的家族類或亞類關系密切，因此對酶分類問題的研究十分必要。近年來對酶的家族類的分類研究已經比較完善，故如今的熱點變為了酶亞類的分類預測。

本文基于酶的序列信息，分別使用矩陣打分與離散增量的方法提取各類特征參數，然后將多種特征參數有效組合，利用支持向量機分類算法對數據集中酶家族類的各個亞類進行分類識別。計算結果表明，此算法能夠獲得較高的預測成功率。

1 材料與方法

1.1 數據集的選取

本文使用的酶序列來源于ENZYME數據集http://www.expasy.org/enzyme/(released on 01-May-2007)，和Chou等人使用的數據集相同[4]。按照以下3個標準來選取數據集：①選取長度均大于50個殘基的序列；②刪除同時屬于多種類型的酶序列；③酶序列的相似性小于40%。基于以上標準可以得到： 18個亞類的1820條氧化還原酶序列；8個亞類的2847條轉移酶序列；5個亞類的3279條水解酶序列；6個亞類的892條裂合酶序列；6個亞類的639條異構酶序列；6個亞類的965條合成酶序列。

1.2 計算方法

1.2.1 矩陣打分方法

矩陣打分方法已被成功應用于蛋白質β-發夾模體的識別[5]、蛋白質折疊子的預測[6]等方面。由于酶序列片段具有很強的位點保守性，故使用矩陣打分方法來提取特征參數，此方法的應用分為以下4步。

這里，i = 1,2,…, L (L為酶序列片斷的截取長度)，j表示20種氨基酸和1個空位，iN表示在第 i個位置氨基酸出現的總頻數，ijn表示在第i個位置第j種氨基酸出現的頻數[7]。

②依據位點的位置概率，構造21行L列的位置權重矩陣：

其中，0jP 表示第j種氨基酸的背景概率[7]。

③計算酶序列中第i個位點的保守性參量：

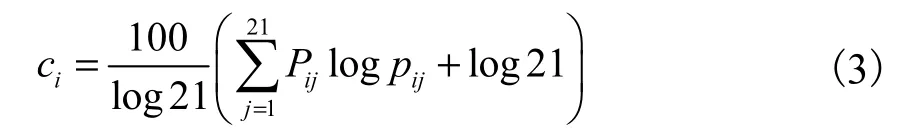
④使用位置權重矩陣，對于任意一段給定的酶序列片段進行打分，定義打分函數(S)為：

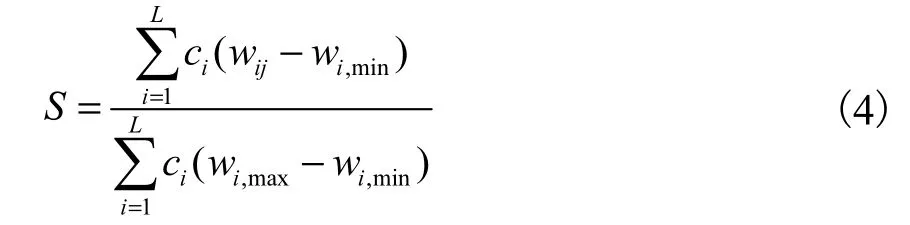
其中，,maxiw 和,inimw 分別表示第i行矩陣元的最大值和最小值，這里0 1S≤ ≤ 。

以氧化還原酶為例，利用氧化還原酶包含的18個亞類的數據集可以得到18個位置權重矩陣，對于任意一段給定的酶序列片段，由(4)式可以得出18個打分值，比較這18個分值的大小，哪一個亞類的分值高，此序列片段就被判斷為屬于哪一類別的亞類。類似的，轉移酶、水解酶、裂合酶、異構酶和合成酶分別也據此判斷。

截取酶序列片段的原則：①由于酶序列的N端與C端所反映的位點保守性差異很大，需分別從酶序列的N端與C端截取氨基酸片段進行矩陣打分的分類預測，通過比較，選取包含70個氨基酸殘基的片段長計算效果最佳；②為了不影響計算結果，對酶序列的長度作了統計分析，如表1所示，發現序列 長≤140個氨基酸殘基的序列數在各類中都＜6.13%；③以氧化還原酶為例，從酶序列的N端和C端分別截取70個氨基酸殘基的片段長進行打分，任意一條待測序列得到18×2個打分值。類似的，轉移酶、水解酶、裂合酶、異構酶和合成酶分別可以得到 8×2、5×2、6×2、6×2和6×2個打分值。

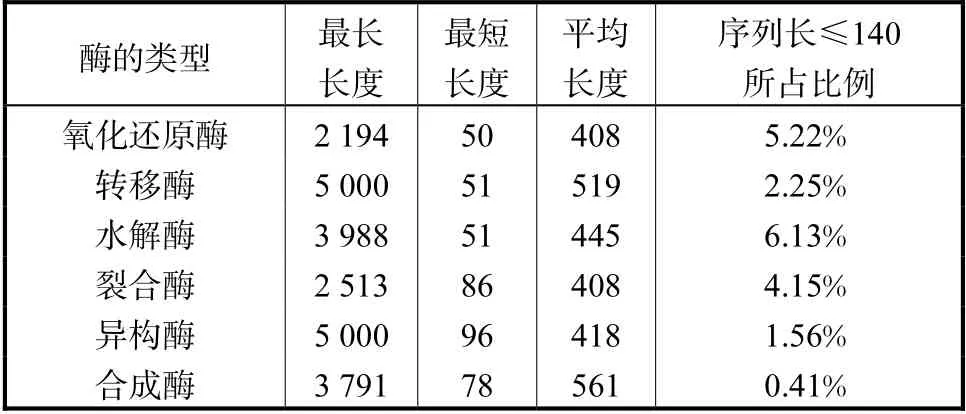
表1 酶的6個家族類序列長度的統計分析 Tab.1 Statistical analysis of sequence length of six families of enzymes

1.2.2 離散增量方法

近年來離散增量方法已在亞細胞定位[8]、蛋白質超家族的預測[9]等工作中大量使用。

在S維空間中，構造2個離散源X：[n1，n2，…，ni，…，ns]和Y：[m1，m2，…，mi，…，ms]，這里ni和mi分別表示第i種氨基酸關聯出現的頻數，它們的離散量分別為：

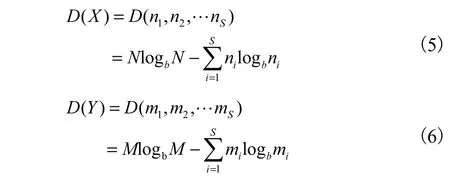
離散增量定義為：

其中，D ( X + Y)為混合離散源X+Y(n1+m1，n2+ m2，…，ns+ms)的離散量，，對數的底b＝10，離散量的單位為哈特。

離散增量定義了2個離散源的同源性程度，離散增量值越小，它們之間的相似性越高[7]。

以氧化還原酶為例，由其18個亞類的數據集可以構成18個標準離散源，對于任意一條酶序列，由(7)式可以求得18個離散增量值，比較它們的大小，哪一個亞類的離散增量值小，此序列就被判斷為屬于哪一類別的亞類。類似的，轉移酶、水解酶、裂合酶、異構酶和合成酶也適用。

根據氨基酸殘基的物理化學、生物化學性質的不同，將20種氨基酸分為以下9類[10]：C；M；N、Q；D、E；S、T；P、A、G；I、V、L；F、Y、W；H、K、R。

本文以酶序列中氨基酸理化性緊鄰關聯與氨基酸次鄰關聯的出現頻數分別構成標準離散源，均計算離散增量值。以氧化還原酶為例，利用氨基酸理化性緊鄰關聯的出現頻數為參數可以得到18個標準離散源，對于任意一條待測序列可以得出18個離散增量值；同樣以氨基酸次鄰關聯的出現頻數為參數也可以得到18個離散增量值。類似的，轉移酶、水解酶、裂合酶、異構酶和合成酶分別可以得到8×2、5×2、6×2、6×2和6×2個離散增量值。

1.2.3 支持向量機方法

支持向量機(SVM)是一個非常強大且具有多種功能的機器學習模型，能夠處理線性或非線性分類問題。SVM是最好的現成分類器(現成指不用修改可以直接使用)，而且它的分類錯誤率較低。SVM特別適合應用于中小型規模數據集樣本的分類問題，能夠解決高維問題，還可以避免神經網絡結構選擇和局部極小點問題[11]。本文使用的是臺灣大學林智仁等人開發的libSVM-3.1版的程序包[12]。libSVM提供了一些簡單易用的接口，使用戶能夠方便應用而不必關心其內部復雜的數學模型和運行過程。

2 結果與討論

以氧化還原酶為例，對任一待測的酶序列，把氨基酸理化性的緊鄰關聯與氨基酸的次鄰關聯分別的出現頻數作為特征參數，使用離散增量方法得到18×2個離散增量值；分別從酶序列的N端與C端截取70個氨基酸殘基片段長進行矩陣打分，得到18×2個打分值；將這36個離散增量值與36個打分值構成的組成向量，共同輸入支持向量機中，使用刀切法(Jackknife)檢驗對氧化還原酶中的亞類進行分類識別，其預測結果見表2。類似的，對其他5個家族類的酶的亞類也做了同樣的分類識別，預測結果在表2中列出。此外，為了方便預測結果的比較，還分別采用前面介紹的矩陣打分方法和離散增量方法對酶家族類的亞類進行預測，同時將Chou等[4]運用相同數據集的Jackknife檢驗的預測結果也列于該表中。

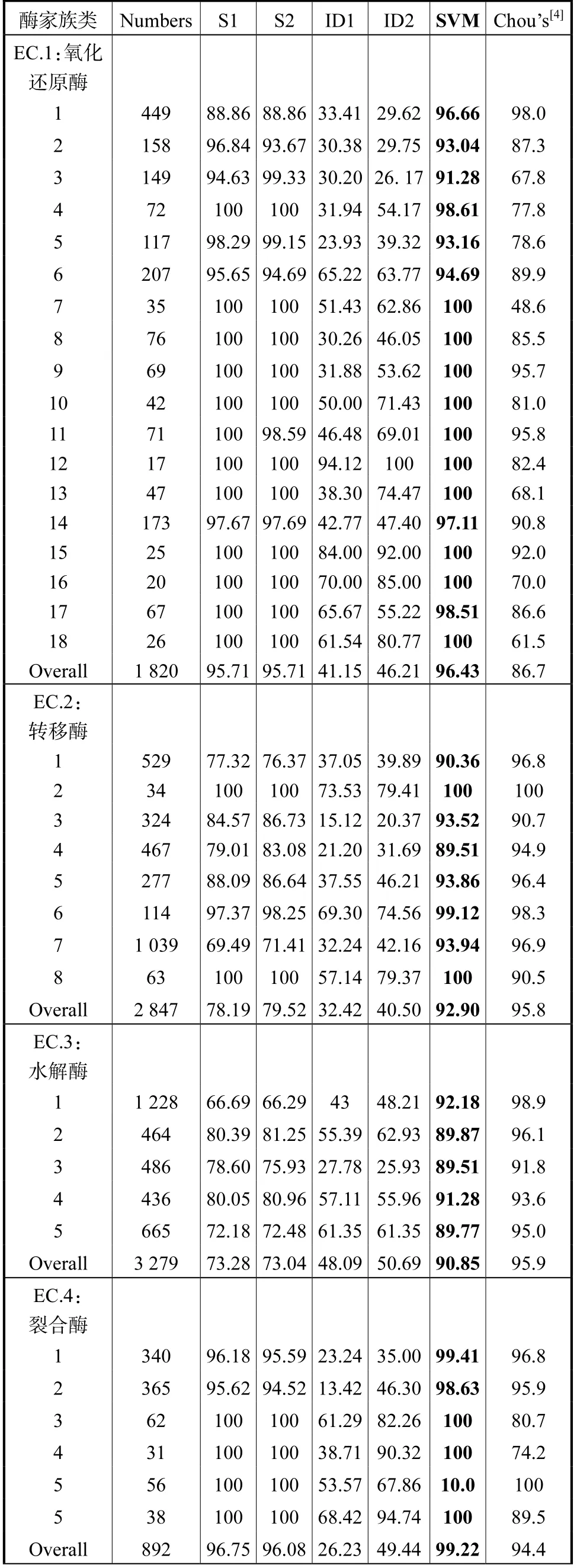
表2 酶的6個家族類中各亞類的Jackknife檢驗下的預測結果 Tab.2 Prediction results of each subclass in six families of enzymes under jackknife test

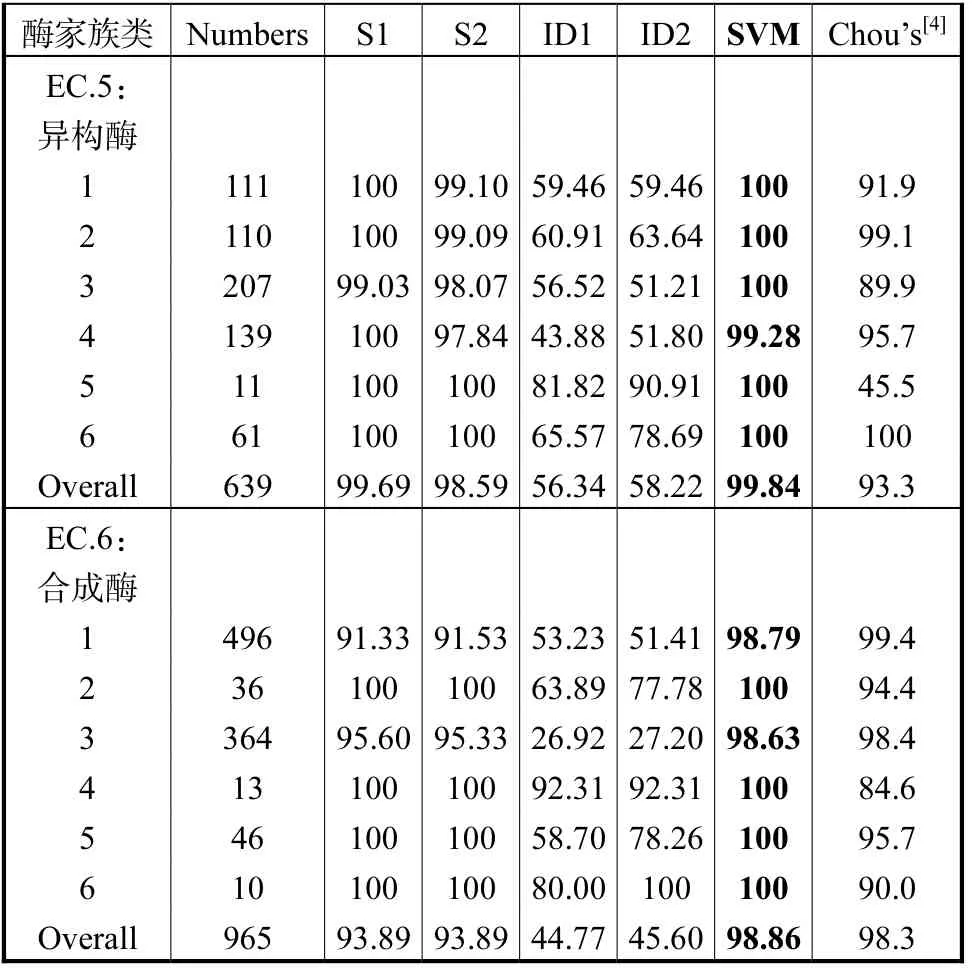
續表2

從表2的預測結果能夠看出，從酶序列的N端和C端截取氨基酸殘基片段的矩陣打分方法預測結果整體上優于離散增量方法的預測結果，進一步表明酶序列的兩端具有很好的位點保守性。而矩陣打分的2種分值結合氨基酸關聯的2種離散增量值共同作為特征參數進行有效的組合，利用支持向量機的分類算法，獲得了最佳的預測結果。不但每個家族類的總體預測成功率很高，而且各個亞類的結果也非常理想。氧化還原酶、轉移酶、水解酶、裂合酶、異構酶和合成酶中亞類的總體預測成功率分別為96.43%、92.90%、90.85%、99.22%、99.84%和98.86%。氧化還原酶、異構酶和裂合酶的總體預測成功率比Chou[4]的方法分別提高了9.73%、6.54%和4.82%，水解酶和轉移酶的總體預測成功率比Chou等[4]的結果稍差。究其原因，是因為水解酶和轉移酶的序列數目很大，故噪聲顯著。由于支持向量機需要大量的內存，選擇正確的核很重要，所以很難做出調整，當數據集的噪聲較大時，無法獲得滿意的結果。

3 結 語

本文基于酶的序列信息，使用多特征的組合向量作為參數對酶的亞家族類進行類型識別，預測成功率有了很大提高。這是因為支持向量機方法具有高效的分類能力，它能夠將各種序列信息有效融合，通過網格化尋找最優參數c值和g值。此方法的優勢還表現在通過提取矩陣打分值和離散增量值的方法，降低了輸入支持向量機的特征參數維數，避免了維數災難，簡化了計算過程。■