一道解三角形真題的多解與反思

山東省青島經濟技術開發區第四中學 王永剛

1 引言

每年的高考真題，總有眾多的亮點，名題薈萃，創新新穎，典型突出，引入注目.此類高考真題，知識融合交匯考點明確，立意突出，科學創新，具有非常好的教學價值，吸引了眾多命題者的引用、模仿與改編等，這些優良的創新“產品”經常出現在一些高考模擬卷中，值得我們細細品賞，好好深入分析與研究.

2 問題呈現

問題(2020屆廣東省廣州市高三年級階段訓練題理科·16)已知△ABC的三個內角為A，B，C，且sinA，sinB，sinC成等差數列，則sin 2B+2cosB的最小值為______，最大值為______.

此題以三角形為載體，結合三角形的三內角的正弦值成等差數列來設置限制條件，進而求解角B所對應的三角關系式的最值.破解此題可分為兩個步驟：(1)利用條件確定角B的取值范圍；(2)在角B的限制條件下確定sin 2B+2cosB的最值.而對應兩個步驟的切入思維多樣，破解方法各異.

3 問題破解

(1)確定角B的取值范圍.

方法1：(三角恒等變換)

由sinA，sinB，sinC成等差數列，可得sinA+sinC=2sinB.

結合三角恒等變換公式，可得

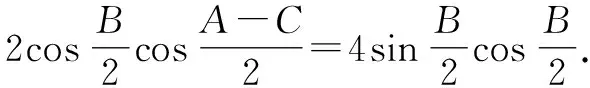
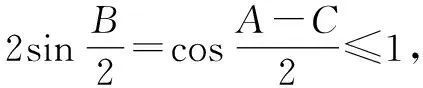
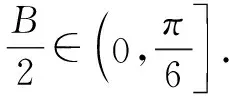
方法2：(基本不等式法)

由sinA，sinB，sinC成等差數列，可得sinA+sinC=2sinB.結合正弦定理，有a+c=2b.

由余弦定理，得

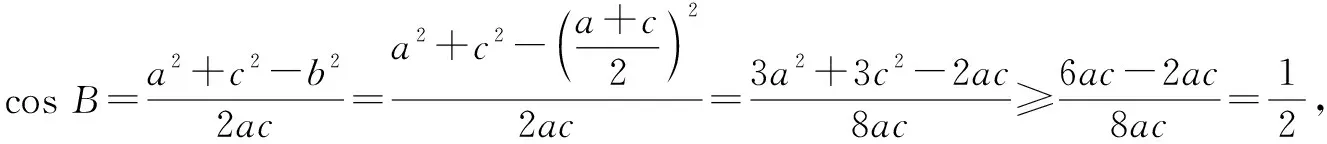
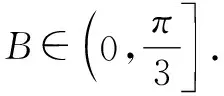
方法3：(橢圓模型法)

由sinA，sinB，sinC成等差數列，可得sinA+sinC=2sinB.結合正弦定理，有BC+BA=2AC.

不妨設AC=2，則BC+BA=2AC=4.

點評：根據題目條件，結合等差中項的應用得到關系式sinA+sinC=2sinB，直接通過三角恒等變換以及三角形的性質可以確定角B的取值范圍，此方法對三角恒等變換公式的要求比較高；而常見的方法是由三角關系式借助正弦定理轉化為邊的關系式，再結合余弦定理及基本不等式來確定角B的取值范圍；利用三角關系式借助正弦定理轉化為邊的關系式，合理構建模型，利用橢圓的方程與幾何性質來確定角B的取值范圍，也是非常不錯的破解方法.

(2)確定sin 2B+2cosB的最值.

方法1：(導數法1)

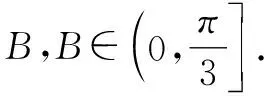
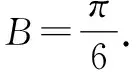
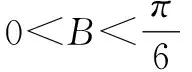
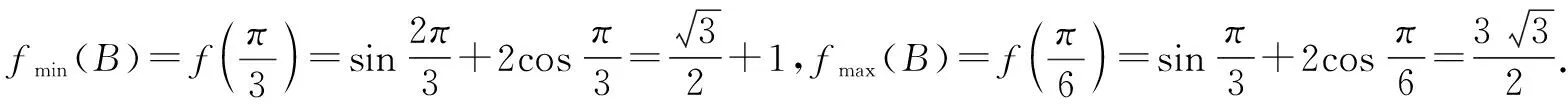
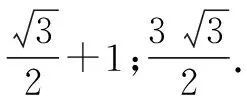
方法2：(導數法2)

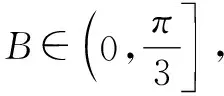
sin 2B+2cosB=2sinBcosB+2cosB

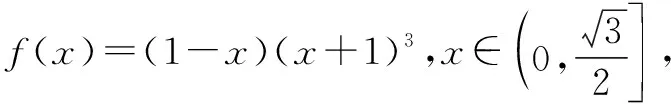
f′(x)=-(x+1)3+3(1-x)(x+1)2

=-2(2x-1)(x+1)2.

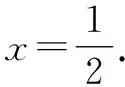
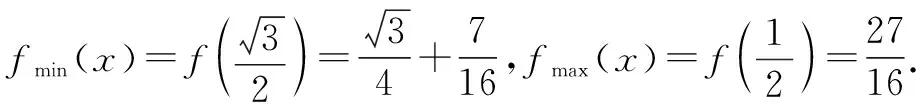
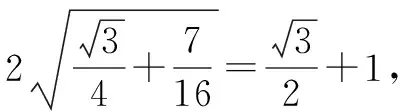
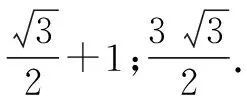
方法3：(換元法)

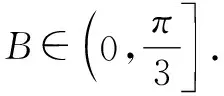
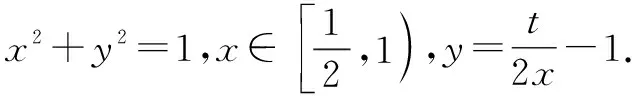
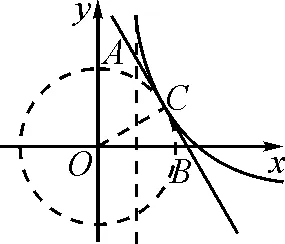
圖1

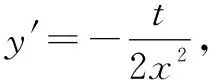
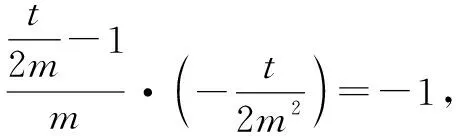
4m4=t2-2mt①

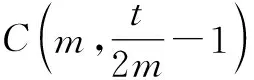
4m4+t2-4mt=0 ②

①②式聯立消去mt,整理可得t=3m.

將t=3m代入4m4=t2-2mt，整理可得

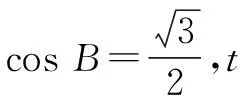
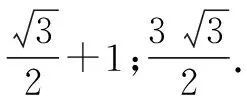
點評：在角B的限制條件下，將所求的三角關系式轉化為一元函數問題，可以借助導數法來確定其最大值與最小值，這是破解此類問題中最常見的思維方式；而結合對應的三角關系式進行合理換元，把三角問題轉化為函數問題，利用相應的軌跡方程以及曲線之間的關系來分析與判斷最值，也是巧妙構建模型，結合數學建模來處理問題的一大創新思維.

4 鏈接高考

事實上，以上問題源自以下高考真題，是在高考真題的基礎上加以探究、拓展與變式，融合知識，提升難度.

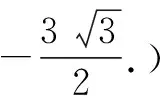
高考真題中所求解的三角函數的最值問題，沒有限制條件，相比更為簡單.而以上問題通過合理設置，將解三角形問題與數列問題融合，給出自變量的取值范圍，并在此基礎上分別求解三角關系式的最大值與最小值，難度相比高考真題來說有較大的提升，而破解方法由于考慮到最大值與最小值的差別，思維切入有所限制.

5 解后反思

對于一些典型高考真題，在學生解決問題的基礎上，教師可以有針對性地加以挖掘、融合、探究、拓展，引導學生聯系教材，充分把握數學知識、數學思想方法的實質，真正形成有效的數學知識體系與思維方法，從而提升知識的掌握程度，拓展數學思維能力，培養良好的數學品質，培育優秀的人文精神.