巨震下設置黏彈性阻尼RC框架結構抗倒塌分析

萬黃晨 張敏

摘? 要：為研究傳統抗震結構設置黏彈性阻尼器對巨震作用的抗倒塌性能，采用增量動力分析（incremental dynamic analysis，IDA）方法，針對II類場地23條具有代表性的巨震波作用對結構樓層位移、能量耗散、結構倒塌的易損性曲線及結構塑性鉸分布等分別進行動力彈塑性分析。工程算例分析表明：巨震作用下，設置黏彈性阻尼器的減震結構樓層最大位移和層間最大位移角均明顯減小，其倒塌概率遠低于相應傳統抗震結構相應值，而抗倒塌安全儲備系數明顯高于相應抗震結構相應值;另外，減震結構塑性鉸遠未達到承載力喪失的程度，而抗震結構的塑性鉸處于承載能力即將失效狀態。由此表明，巨震作用下，黏彈性阻尼器減震結構相較于傳統抗震結構能有效耗散地震能量，改善框架結構的屈服機制，增大結構抗倒塌安全儲備，因而能顯著提高結構抗倒塌性能。

關鍵詞：巨震;黏彈性阻尼器;增量動力分析法;有限元結構模型;動力響應分析

中圖分類號：TU352.1? ? ? ? DOI：10.16375/j.cnki.cn45-1395/t.2022.02.004

0? ? 引言

近年來全球多地發生烈度巨大的地震，如汶川大地震以及“3·11”日本地震等，導致大量建筑倒塌。這些地震烈度較高，遠超罕遇烈度地震的范疇，這種特大地震通常稱為巨震。巨震及其引發的次生災害造成了重大的人員傷亡和財產損失。如何防止或減弱巨震帶來的損失已成為國內外學者關注的熱點。

傳統建筑結構主要是通過增大其承載能力或提高其彈塑性變形能力來抵抗大震的作用。然而在遠超大震水平的巨震作用下，會引起結構較大損傷，甚至發生整體倒塌，如何保證巨震作用下結構不發生倒塌是眾多學者關注的問題。結構振動控制是防震減災的重要技術手段之一，由于黏彈性阻尼器構造簡單，抗剪切穩定性高，微小的振動也能向被加固的結構提供阻尼，并可重復使用，較黏滯阻尼器和金屬阻尼器性價比高[1]，因而得到越來越廣泛的應用。能否通過設置黏彈性阻尼器自身變形耗散地震能量以確保結構在巨震作用下不發生倒塌，是一個值得研究的問題。

目前，眾多學者針對傳統建筑結構在巨震下產生的震害開展了研究。馬玉虎等[2]在漩口中學巨震區同一場地選取10個RC框架進行震害考察，認為抗震目標應該由之前的“大震不倒”向“巨震不倒”轉變。呂大剛等[3]提出由“三級水準設防原則”向“四級水準（巨震）設防原則”轉變，并確定巨震設防風險導向的解析方法，通過指定目標下倒塌概率值計算得到巨震作用下的峰值地面加速度值，這為后續研究提供了理論依據。周云等[4]根據設置黏彈性阻尼器結構的性能特征和響應特點，提出以層間位移為控制函數，并按該函數優化布置阻尼器。李創第等[5-6]基于小震作用下研究了黏彈性阻尼器單自由度隨機響應和多層基礎隔震響應，并且簡化了黏彈性阻尼器在地震激勵下的求解過程。夏雨等[7]研究黏彈性阻尼器的支撐剛度與減震性能間的關系，結果表明黏彈性阻尼器支撐剛度與其減震性能呈正相關。張敏等[8]研究了在小震作用下設置黏彈性阻尼器框架的相關減震性能參數，認為阻尼器支撐剛度達到一定值時，阻尼器支撐基本不影響阻尼器對結構的減震性能，并在此基礎上提出了計算設置黏彈性阻尼器框架地震作用的計算方法。

現階段，大多數文獻主要是對小震作用下設置黏彈性阻尼器結構的減震性能進行研究，而對于巨震作用下黏彈性阻尼器的減震性能研究相對較少。鑒于此，本文針對按抗震要求配筋的框架結構設置黏彈性阻尼器，在II類場地23條具有代表性的巨震波作用下，研究該結構能否實現“巨震不倒”的目標，并針對該結構進行巨震作用彈塑性動力響應分析，主要包括結構彈塑性層間位移分析、結構自身耗能分析、阻尼器耗能分析、結構易損性分析、以及結構塑性鉸分布分析，進而研究結構設置黏彈性阻尼器框架在巨震作用下的抗倒塌性能。

1? ? 基于IDA的易損性分析法

1.1? ?增量動力分析（IDA）的基本原理

增量動力分析 （incremental dynamic analysis，IDA） [9-10]是一種可以對結構進行精細定量分析的彈塑性研究方法，可對結構的地震易損性進行量化評估。IDA法將一組地震波按比例系數縮放后加載在結構上，通過逐步增加步長，得到結構的非線性時程響應，從而獲得地震動強度指標（intensity measure，IM）和結構破壞指標（damage measure，DM）之間的關系，最后繪制成曲線，這條曲線即為IDA曲線。

1.2? ?地震波的選取

理論上選取地震波數量和種類越多，分析結果越精確，由此產生的工作量也會相應增加。因此，選取合理的地震波數量至關重要。黃煒元等[11]對中等高度的建筑進行增量動力分析研究，結果表明，取22條地震動記錄可以滿足較精確的地震分析需求。本文選取適用于Ⅱ類場地的4條人工地震波和19條實際觀測記錄的地震波，共計23條地震波。

1.3? ?地震動強度指標IM的選取

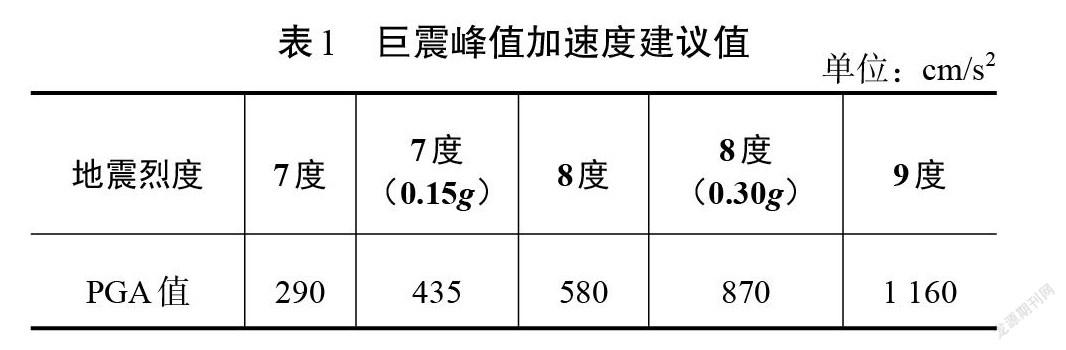
地震動強度指標主要有峰值地面加速度（peak ground acceleration，PGA）、峰值地面速度（peak ground velocity，PGV）、加速度反應譜（acceleration response spectrum，簡稱Sa（T1））等，為了與《建筑抗震設計規范》（GB 50011—2010）[12]中規定的設防烈度更好地對接，本文選用PGA作為地震動強度指標。根據文獻[13]和表1中給出的建議值，選擇超越概率為萬年一遇的地震峰值加速度為巨震峰值加速度，見表1。故設防地震烈度為8度（0.30g）的巨震峰值加速度應為870 cm/s2。

表1? ? 巨震峰值加速度建議值

[地震烈度 7度 7度

（0.15g） 8度 8度

（0.30g） 9度 PGA值 290 435 580 870 1 160 ]

1.4? ?結構破壞指標DM的選取

常用的DM指標主要有結構層間最大位移角、頂層位移、層間位移等，文獻[14]詳細分析了結構性能指標和地震動水平衡量指標對結構的影響以及選用建議。《建筑抗震設計規范》（GB 50011—2010）將彈性和彈塑性層間最大位移角[θmax]作為判定結構安全性能的指標。在巨震作用下，結構通常都會發生彈塑性變形，為了對接規范，本文以彈塑性層間最大位移角[θmax]作為結構倒塌破壞指標。根據《建筑抗震設計規范》（GB 50011—2010）規定，鋼筋混凝土結構處于倒塌狀態的彈塑性層間最大位移角[θmax]的臨界值為1/50。

1.5? ?易損性分析步驟

基于IDA的易損性分析基本步驟如下：

Step 1? 建立結構彈塑性分析模型。

Step 2? 根據結構所在場地及震害信息，選用m條地震動記錄與合適的IM指標。在某一地震波的IM指標下加載地震波，對混凝土框架結構分別進行彈塑性動力時程分析，若結構在給定IM指標下共有n條地震波的IM指標超過限定值，此時可認為在這n條地震波的作用下結構將發生倒塌，那么在該地震動強度下結構發生倒塌的概率為n/m，本文的m取23。

Step 3? 由較低地震動強度指標固定步長逐步增大，重復Step 2，直到IM指標達到限值，得到該結構在不同IM指標下的DM指標。

Step 4? 結構在選定IM指標下達到或超過給定臨界值的概率，用超越概率[Pf]表示，其表達式? ? 如下：

[Pf（μD≥μC/SIM）=φ（lnμD-lnμCβ2D+β2C）]，? ? ? ? （1）

式中：[φ（·）]為標準正態分布的累計概率函數，[SIM]為地震動強度指標值，[μD]為結構地震需求反應函數，[μC]為結構抗震能力概率函數， [μD]、[μC]分別為[μD]與[μC]的均值，[β2D]與[β2C]分別為[μD]與[μC]的對數標準差。根據文獻[15]研究結論，[μD]與[μC]均服從對數正態分布，當以PGA為變量時，[β2D+β2C]取0.5。

ATC-63報告[16]中建議采用抗倒塌安全儲備系數[σCMR]（collapse margin ration，CMR）作為量化評價結構抗倒塌能力大小的指標。湯保新等[17]將[σCMR]定義為50%倒塌概率的地震動強度指標值[SIM50%倒塌]與相應的結構設防大震的地震動強度指標值[SIM設防大震]之比，即：

[σCMR=SIM50%倒塌SIM設防大震] .? ? ? ? ? ? ? ? ? ? ? ? ? （2）

2? ? 有限元結構模型的建立

2.1? ?結構信息

本文的工程算例為一棟10層鋼筋框架結構。設計地震分組為第二組，Ⅱ類場地土，抗震設防烈度為8度（0.30g），設防類別為丙類，結構自身阻尼比為5%。本結構總高度為34.2 m，首層高度為? ? ?4.0 m，標準層高度為3.3 m;框架梁的截面尺寸均為[300? mm×600? mm]，框架梁的縱筋型號采用HRB400;柱子的截面尺寸均為[600? mm×750? mm]，柱子的受力縱筋型號采用HRB400;箍筋型號均采用HPB300。本結構梁柱均采用[C40]混凝土，屋面與各樓層恒荷載標準值均為[4.5] [kN/m2]，活荷載標準值均為[2.0] [kN/m2]，框架梁上墻體自重折算后的標準值為[3.2] [kN/m]。結構的平面如圖1所示，分析一榀框架（計算單元如圖1陰影所示），根據PKPM設計軟件計算結構框架梁與柱配筋如圖2所示，圖中各數分別為結構梁柱單側配筋面積，單位為[mm2]。

圖2框架結構在各樓層設置黏彈性阻尼器以增強減震性能，防止巨震作用下上述框架結構發生 倒塌。

2.2? ?黏彈性阻尼器參數確定與布置方式

本文采用的黏彈性阻尼器是一種與阻尼器兩端相對速度相關的平動式耗能器，采用Maxwell力學模型[18]來模擬黏彈性阻尼器。即一個彈簧單元與阻尼單元串聯，如圖3所示，該模型為理想狀態下的Maxwell力學模型。

Maxwell的模型力學關系如下：

[dc（t）+dk（t）=d（t）]，? ? ? ? ? ? ? ? ? ? ?（3）

[Kddk（t）=Cddc（t）=fd（t）].? ? ? ? ? ? ? ? （4）

經過傅里葉變換得：

[Dk（ω）+Dc（ω）=D（ω）]，? ? ? ? ? ? ? ? ? （5）

[KdDk（ω）=iωCdDc（ω）=Fd（ω）]，? ? ? ? ? ? （6）

式中：[Cd]和[Kd]分別為黏彈性阻尼器的阻尼系數和彈簧單元剛度系數， [dc（t）]和[dk（t）]分別為阻尼單元和阻尼器彈簧單元的位移，[d（t）]為該阻尼器兩端的相對位移，[fd（t）]為黏彈性阻尼器的阻尼力，[ω]為諧振的圓頻率，[Dc（ω）]和[Dk（ω）]分別為[dc（t）和dk（t）]的傅里葉變換，[D（ω）]為[d（t）]的傅里葉變換，[Fd（ω）]為[fd（t）]的傅里葉變換。

令[Fd=K*（ω）D（ω）]，代入式（5）、式（6）中得到：

[K*（ω）=Cdηω2+iCdω1+η2ω2]，? ? ? ? ? ? ? ? ? ? ?（7）

[η=CdKd].? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （8）

式中：[η]為[fd（t）]的松弛時間系數，[K*（ω）]為黏彈性阻尼器的復剛度，[i=-1]。相關研究表明，黏彈性阻尼器的抗震能力由松弛時間系數和阻尼器的阻尼系數共同決定，因此，選取合適的阻尼器參數對結構的抗震能力至關重要。根據文獻[9]，本文各層阻尼器均取[η=0.1]，當阻尼器在各樓層水平設置時，各樓層阻尼器阻尼系數均取[Cd=5.0×107] N·s/m。

參照文獻[19]，阻尼器宜在樓層連續布置，不宜間斷，且宜在樓層平面對稱分布。

阻尼器在實際工程中一般按樓層對角線方式傾斜安裝。因此，本文采用SAP2000軟件建模時阻尼器沿樓層對角線布置。根據力學原理，沿樓層對角線傾斜布置阻尼器的阻尼力與水平布置阻尼器的阻尼力的力學關系可按下列推導。

為了使阻尼器沿樓層對角線傾斜布置與水平布置達到同樣的減震效果，阻尼器的阻尼力應滿足下列關系。

當阻尼器水平布置時：

[Fd=Cd?u]，? ? ? ? ? ? ? ? ? ? ? ?（9）

當阻尼器斜向布置時：

[Fd=Cd?（ucosθ）].? ? ? ? ? ? ? ? ?（10）

假設結構水平振動，上述2種布置方式的阻尼力應滿足下列要求：

[Fd=Fd?cosθ]，? ? ? ? ? ? ? ? ? （11）

由式（9）—式（11）化簡得：

[Cd=Cd（cosθ）2]，? ? ? ? ? ? ? ? ? ? ?（12）

式中：[Fd、Fd]分別為水平式和斜撐式布置阻尼器的作用力，[u]為層間位移，[Cd、Cd]分別為水平式和斜撐式布置阻尼器的阻尼系數，[θ]為斜撐式布置阻尼器與水平樓面的夾角。

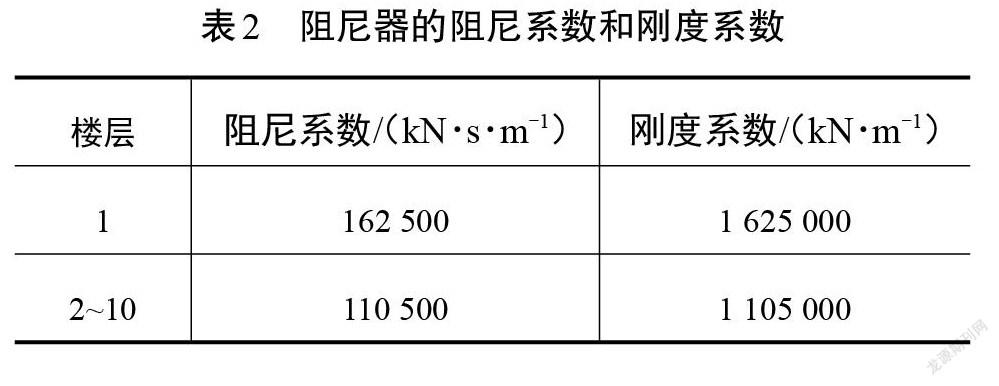
考慮第一樓層層高與其他樓層的區別，根據式（12），各樓層黏彈性阻尼器的阻尼器系數調整如 表2所示。

根據文獻[19]及上述分析，本工程將各樓層阻尼器按圖4連續布置在對角線上。

3? ? 動力響應分析結果

3.1? ?樓層最大位移與層間最大位移角響應

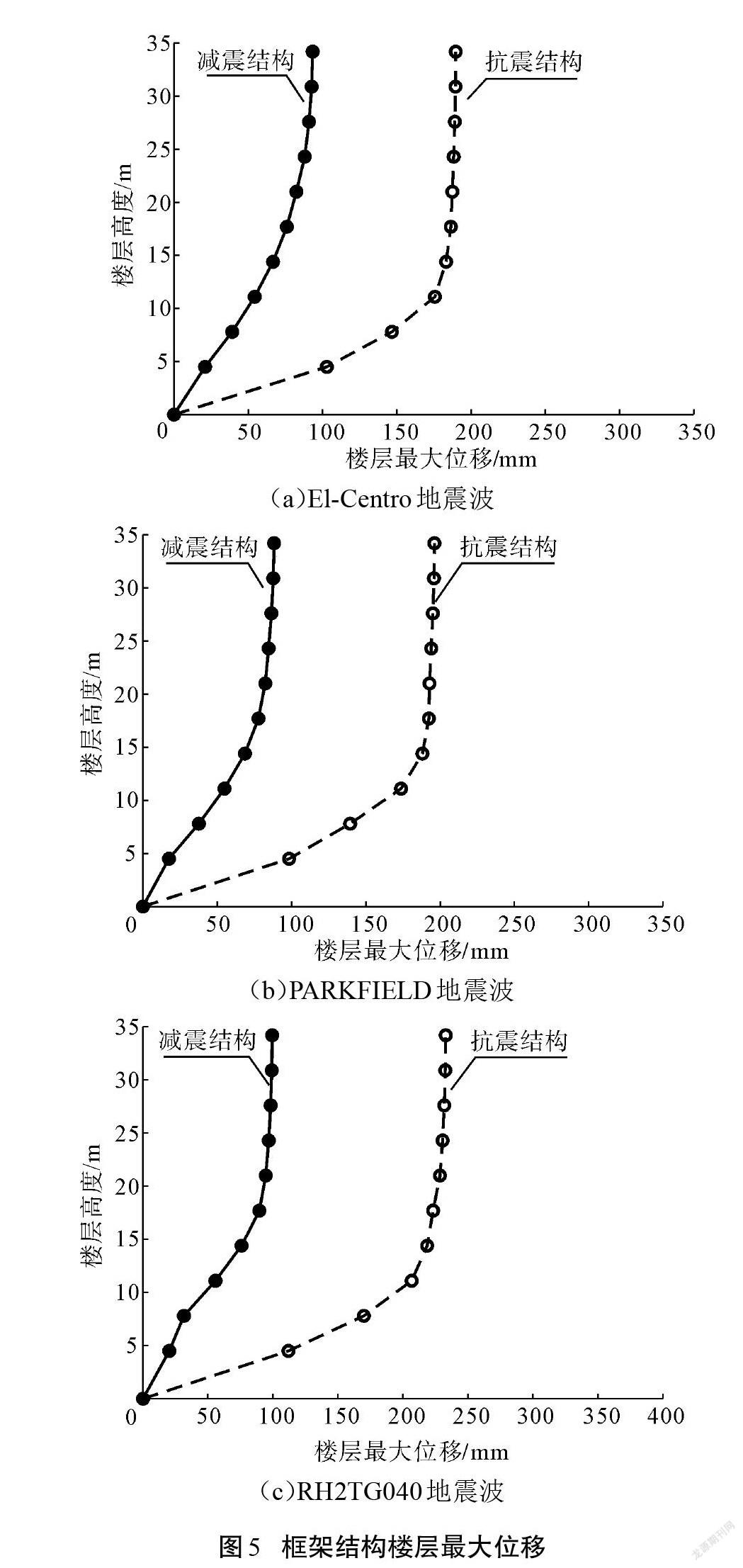
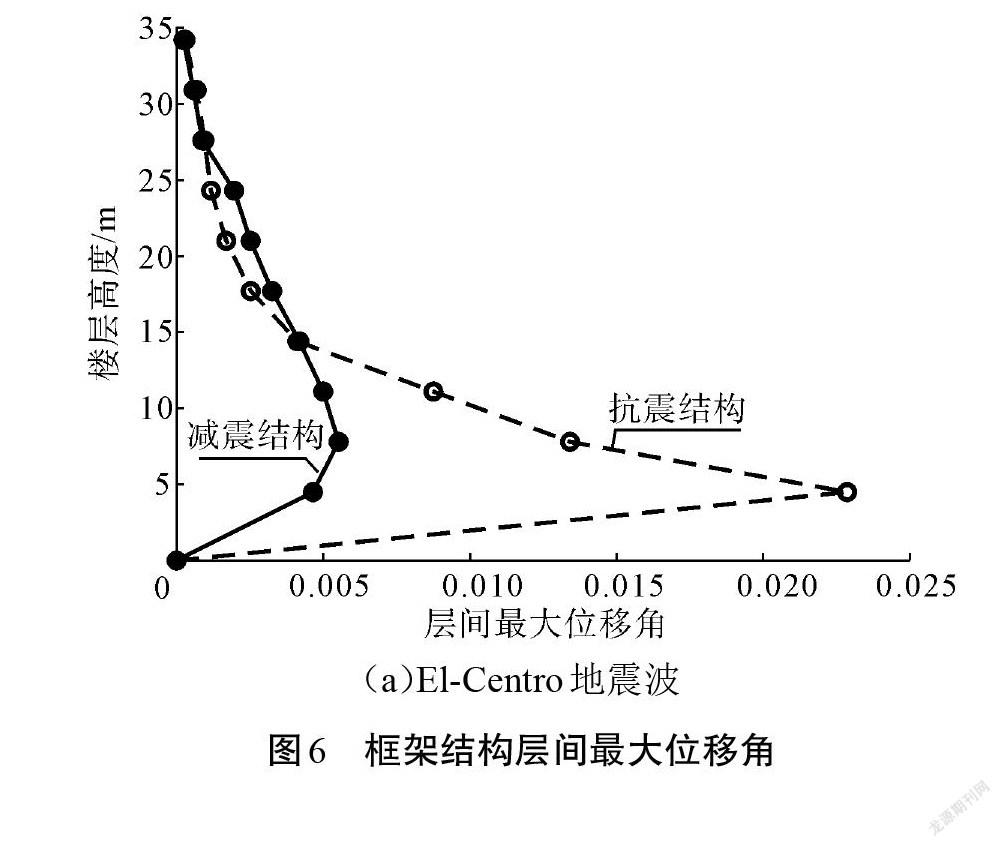
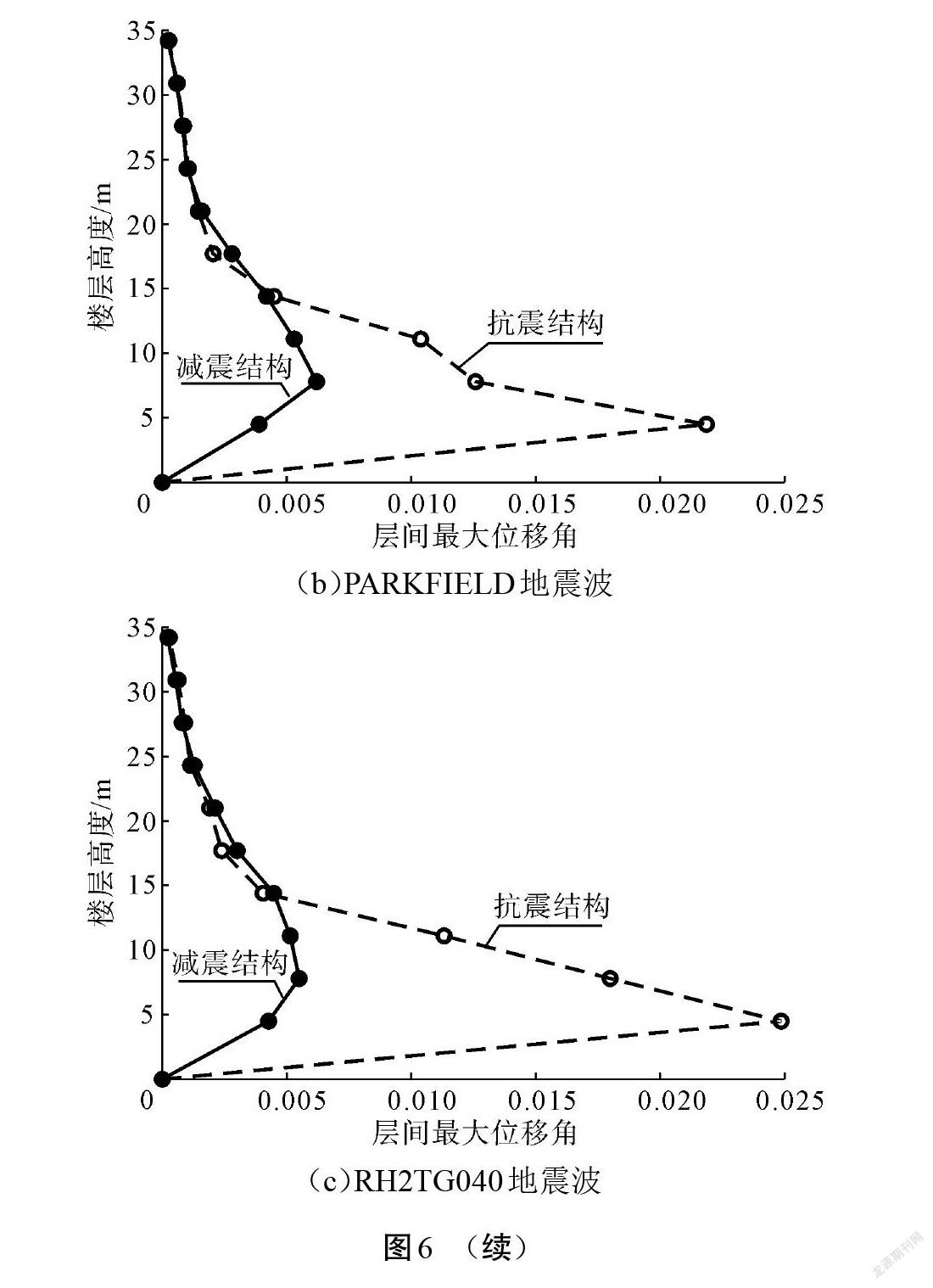
采用SAP2000軟件模擬傳統無阻尼器抗震結構（簡稱抗震結構，下同）和設置黏彈性阻尼器的減震結構（簡稱減震結構，下同），分別在23條地震波作用下進行研究，計算抗震結構和減震結構的樓層最大位移和層間最大位移角響應，使用Matlab軟件繪圖。限于篇幅原因，僅列出El-Centro、PARKFIELD和RH2TG040這3條巨震波作用下的響應結果，分析表明其他20條地震波作用效果與上述3條地震波類似。

在巨震作用下，由圖5和圖6可看出，在設置黏彈性阻尼器后，減震結構樓層最大位移較抗震結構相應值顯著減小，這在上部樓層表現尤其明顯。結構的層間最大位移角均出現在結構底部。而抗震結構底層的層間最大位移角均接近甚至超過《建筑抗震設計規范》（GB 50011—2010）中彈塑性層間最大位移角，這表明傳統抗震結構薄弱部位在結構首層，且在巨震作用時已經接近或者發生倒塌。對比之下，減震結構均未發生倒塌現象。相對于傳統抗震結構，結構薄弱部位最大層間位移角降低均在50%以上，表明黏彈性阻尼器能夠有效抵抗巨震作用，具有較強的減震性能。

3.2? ?結構能量分析

在巨震作用下，傳統抗震結構依靠自身變形來耗散地震能量，而設置黏彈性阻尼器后框架結構通過阻尼器滯回變形以耗散地震能量。本文針對23條地震波，分別記錄了抗震結構和減震結構在巨震作用下的能量。結構能量之間的關系見式（13）：

[EI=EH+EDP+EDC]，? ? ? ? ? ? ? ? ? ? （13）

式中：[EI]為地震輸入結構框架的總能量，[EH]為框架結構自身的總滯回耗能，[EDP]為阻尼器耗能，[EDC]為框架結構自身阻尼耗能。

由于各地震波持時不同，選取每條地震波單位時間內的耗能平均值，23條地震波作用下的結構能量分析見表3。由表3可知，在巨震作用下，地震輸入減震結構與相應抗震結構的總能量相差無幾。在減震結構中，黏彈性阻尼器消耗了大部分在抗震結構中本應該由結構自身耗散的能量，大大降低了結構自身的總滯回耗能，減少了彈塑性損傷，因此，減震結構的自身總阻尼器耗能（[ED]）與地震輸入總能量之比[ED/EI]遠大于傳統抗震結構，表明減震結構有更好的抗震性能。

3.3? ?黏彈性阻尼器耗能分析

以El-Centro波（持時30.02 s）為例，經分析表明其他波作用下阻尼器滯回曲線及各樓層阻尼器耗能與El-Centro波類似。

圖7和圖8分別為El-Centro波作用下，第1層和第10層黏彈性阻尼器的滯回曲線及結構各樓層阻尼器的耗能分布曲線。從圖7可見，黏彈性阻尼器的滯回曲線的形狀比較飽滿，呈現“梭形”，結構底層的滯回環面積較大，表明其在底層耗散了大部分地震輸入結構的能量。由圖8可知，黏彈性阻尼器在底層的滯回環曲線面積最大，阻尼器耗能由下部樓層到上部樓層依次減少，因而結構底部阻尼器耗能作用大于上部樓層。在巨震作用下，抗震結構底部彈塑性層間位移較大，因而底部受損傷程度較嚴重，設置黏彈性阻尼器能顯著降低結構底部的損傷，提高結構的減震能力。

3.4? ?結構易損性分析

根據第1.5節步驟，使用SAP2000對減震結構和相應抗震結構分別進行非線性動力時程分析得到相關數據，導入式（1）可計算出減震結構和相應抗震結構的倒塌概率。研究表明地震反應函數和抗震概率函數呈現對數正態分布，將所得數據擬合成曲線，得到結構倒塌易損性曲線，如圖9所示。由圖9可知，按我國抗震規范設計的傳統抗震框架結構，抵抗巨震作用的能力明顯不足，巨震作用下，發生倒塌的概率較大，倒塌概率大概為48%。設置黏彈性阻尼器框架結構在巨震作用下的倒塌概率曲線隨著地震動增大而緩慢上升，表明黏彈性阻尼器能有效降低結構在巨震作用下的彈塑性動力響應，在地震加速度0.87g處，倒塌概率很小，因而顯著提高了結構巨震作用的抗倒塌性能。

據式（2）可計算出傳統抗震結構和相應減震結構的抗倒塌儲備系數[σCMR]，分別為1.80和3.14，可見在設置黏彈性阻尼器后，[σCMR]值明顯增大，結構的抗倒塌性能得到了顯著的提高。

3.5? ?結構塑性鉸分布

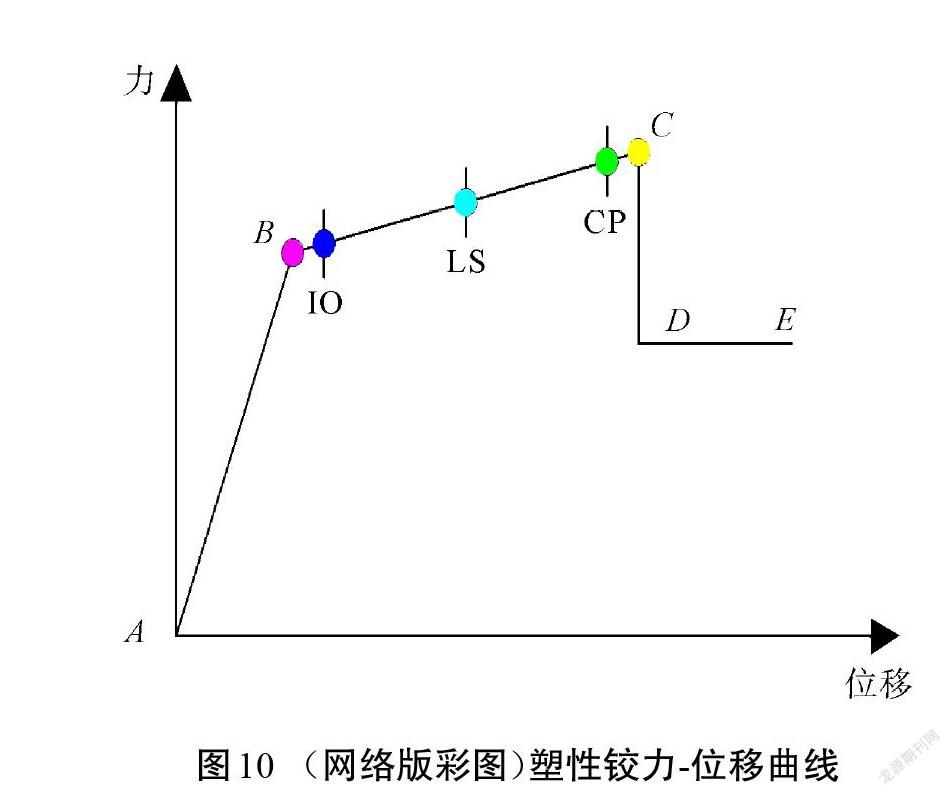
在SAP2000中，通常使用自定義鉸來模擬塑性變形后的結構性能。本文使用主方向的彎矩鉸來模擬梁中間處產生的塑性鉸，用剪力鉸來模擬梁兩端產生的塑性鉸，使用PMM相關鉸來模擬柱產生的塑性鉸。圖10為SAP2000軟件中塑性鉸力-位移曲線，A是起始點;B代表鉸的屈服點，即彈塑性變形的臨界點;C代表結構的承載力逐漸開始喪失;D代表殘余強度;E代表構件完全失效。其中，超過B的塑性鉸變形將被鉸顯現。根據SAP2000中文版使用指南[20]中規定：塑性鉸的能力水平分別用點IO（立即使用）、LS（生命安全）、CP（防止倒塌）來表示，并分別用品紅色、藍色、青色、綠色、黃色來表示。

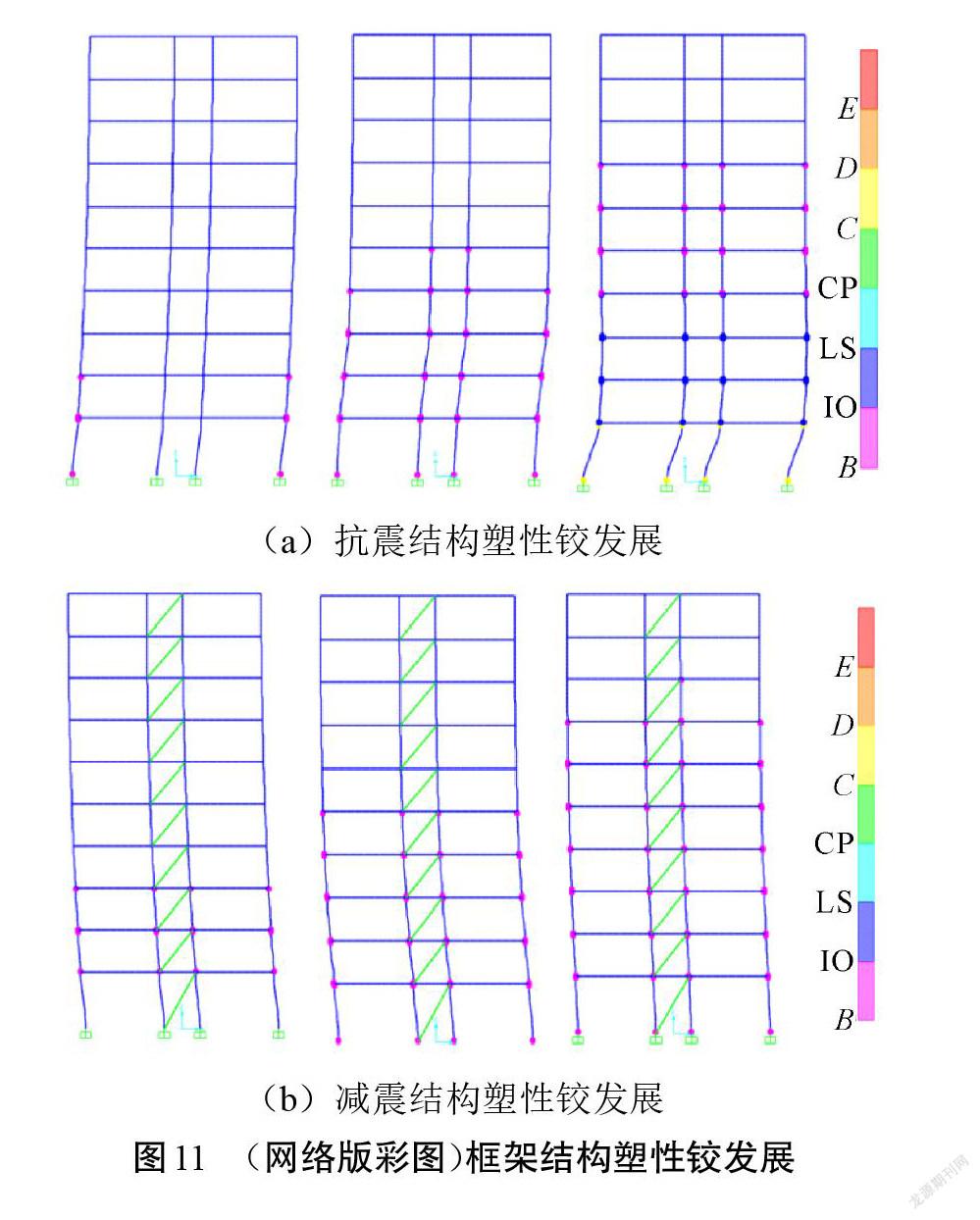
在巨震作用下，減震結構與相應抗震結構框架在El-Centro波作用下的塑性鉸發展過程及分布情況如圖11所示。由圖11可知：1）地震剛開始時，塑性鉸最先出現在結構底層的柱端，此時兩結構均處于IO和LS狀態，其中抗震結構首先出現塑性鉸，發展較快，減震結構的塑性鉸隨后出現。2）隨著地震波持續加載，傳統抗震結構底層塑性鉸很快出現承載力喪失的現象，結構出現較大變形，塑性鉸由下往上快速發展。雖然減震結構在底層也出現了塑性鉸，但基本處于IO和LS狀態，遠未進入失效狀態。

通過分析發現，其他22條地震波在巨震作用下結構塑性鉸發展與此波相似。

4?   結論

通過分析一個10層框架結構工程案例，研究了黏彈性阻尼器減震結構與相應傳統抗震結構在巨震作用下的動力響應，結論如下：

1）相比于傳統抗震結構，設置黏彈性阻尼器的減震結構在最大層間位移、層間最大位移角、結構自身耗能上均表明其有著良好的抗震性能，顯著增強了結構抵抗巨震作用的能力。

2）結構樓層設置的黏彈性阻尼器滯回曲線圖形比較飽滿，表明阻尼器耗能較大。在結構底部樓層耗能較大，表明黏彈性阻尼器顯著降低了結構底部樓層的最大層間位移角，顯著降低結構損傷，從而提高了結構抵抗巨震作用的能力。

3）在巨震作用下，減震結構的抗倒塌安全儲備系數CMR值明顯高于相應抗震結構CMR值，表明黏彈性阻尼器能大量耗散地震動輸入結構的能量，顯著提高減震結構在巨震下的抗倒塌安全性能。

4）抗震結構和減震結構在地震剛開始時在底層均出現塑性鉸。隨著時間的推移，抗震結構的塑性鉸逐步向上擴展，而減震結構的塑性鉸略微向上擴展，且均處于IO和LS狀態，遠沒有到承載力喪失的程度，表明黏彈性阻尼器能有效減少結構的塑性變形，改善結構的屈服機制。

參考文獻

[1]? ? ?張耀笑. 金屬阻尼器與黏彈性阻尼器兼用的高層鋼框架結構減震性能研究[D]. 鎮江：江蘇科技大學，2017.

[2]? ? ?馬玉虎，陸新征，葉列平，等. 漩口中學典型框架結構震害模擬與分析[J]. 工程力學，2011，28（5）：71-77.

[3]? ? ?呂大剛，周洲，王叢，等. 考慮巨震的四級地震設防水平一致風險導向定義與決策分析[J]. 土木工程學報， 2018，51（11）：41-52.

[4]? ? ?周云，徐趙東，鄧雪松. 黏彈性阻尼結構中阻尼器的優化設置[J]. 世界地震工程，1998，14（3）：3-5.

[5]? ? ?李創第，朱騰飛，柏大煉，等.實用黏彈性阻尼器耗能結構非平穩地震響應的快速求解[J].廣西科技大學學報，2018，29（4）：13-20.

[6]? ? ?李創第，陶欣欣.設置粘彈阻尼器的基礎隔震結構平穩響應分析[J].廣西科技大學學報，2015，26（2）：20-25，30.

[7]? ? ?夏雨，李錦博，余穎燁.帶支撐黏彈性阻尼器弱非線性耗能結構的隨機地震響應分析[J].廣西科技大學學報，2021，32（3）：21-26.

[8]? ? ?張敏，龐華英. 帶支撐黏彈性阻尼器框架減震性能分析[J]. 應用力學學報， 2020，37（1）：418-426，498.

[9]? ? ?KIM J，LEE S，CHOI H. Progressive collapse resisting capacity of moment frames with viscous dampers[J]. The Structural Design of Tall and Special Buildings，2013，22（5）：399-414.

[10]? ?BAKER J W，CORNELL C A. A vector‐valued ground motion intensity measure consisting of spectral acceleration and epsilon[J]. Earthquake Engineering and Structural Dynamics，2005，34（10）：1193-1217.

[11]? ?黃煒元，張超，周云，等. 基于IDA的鉛黏彈性阻尼減震結構地震易損性研究[J]. 土木與環境工程學報， 2021，43（3）：75-82.

[12]? ?中華人民共和國住房和城鄉建設部. 建筑抗震設計規范：GB 50011—2010 [S]. 北京：中國建筑工業出版社， 2010.

[13]? ?姚攀峰，呂大剛. 結構工程中巨震峰值加速度的探討[C]//中國土木工程學會. 第九屆全國防震減災工程學術研討會論文集. 2016：41-51.

[14]? ?劉慧杰. 基于增量動力分析的RC框架結構地震易損性研究[D]. 西安：長安大學，2019.

[15]? ?VAMVATSIKOS D，CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics，2002，31（3）：491-514.

[16]? ?Federal Emergency Management Agency. Quantification of building seismic performance and factors：FEMA P695[R]. Washington DC，2009.

[17]? ?湯保新，葉列平，陸新征. 丙類與乙類設防RC框架結構抗地震倒塌能力對比[J]. 建筑結構學報，2011， 32（10）：30-38.

[18]? ?李創第，王博文，昌明靜. 設置支撐的廣義Maxwell阻尼耗能結構系統均勻與非均勻隨機地震響應分析[J]. 桂林理工大學學報， 2020， 40（3）：523-529.

[19]? ?張敏，龐華英. 設置黏彈性阻尼耗能框架結構減震性能分析[J]. 計算力學學報，2019，36（6）：739-746.

[20]? ?北京金土木軟件技術有限公司. SAP2000中文版使用指南[M]. 北京：人民交通出版社，2012.

Collapse resistance analysis of RC frame structure with viscoelastic damping under mega earthquake

WAN Huangchen1， ZHANG Min*1，2

（1. School of Civil Engineering， East China Jiaotong University， Nanchang 330013， China;

2. School of Civil Engineering， Jiangxi Science and Technology Normal University， Nanchang 330000， China）

Abstract： The collapse resistance of frame structure with viscoelastic dampers is studied. For the frame structure subjected from 23 representative mega earthquake waves in the class II site， the incremental dynamic analysis method is used for dynamic elastoplastic study of the floor displacement， energy? ? ?dissipation， collapse vulnerability curve and distribution of structural plastic hinge. The analysis of? ? ?engineering example shows that the floor displacement and the story layer angle of the damping? ? ?structure with viscoelastic dampers are obviously reduced under the mega earthquake， the collapse? probability is much lower than the corresponding value of the traditional frame structure without? ? ? ?viscoelastic damper， but the safety reserve coefficient of collapse resistance is obviously higher than the corresponding value of the traditional structure. In addition， the plastic hinges of the damping structure are far from bearing capacity loss， but the plastic hinges of the traditional frame structure are in the state of bearing capacity failure. From this， the viscoelastic damper structure can effectively dissipate the seismic energy， improve the yield mechanism of the frame structure， and increase the structural collapse resistance safety reserve， so the viscoelastic dampers can significantly improve the collapse resistance performance of the structure.

Key words： mega earthquake; viscoelastic damper; incremental dynamic analysis; finite element? ? structural model; dynamic response analysis

（責任編輯：羅小芬）