RVM在煤自燃預測中的應用研究

王 丹

(晉能控股煤業集團 四老溝礦，山西 大同 037000)

礦井采空區遺煤自然發火不但對礦井安全生產有嚴重的威脅，而且可能會引發采空區瓦斯爆炸，嚴重威脅井下作業人員的生命安全[1-2]。有效地預防采空區遺煤自然發火是確保礦井安全生產的重要之舉，而準確預測采空區遺煤的自然發火是降低煤自燃對安全生產威脅的關鍵。在煤自然發火時，采空區遺煤自然發火標志性氣體的濃度因煤發生不同氧化程度而改變，所以利用檢測檢驗技術研究自燃階段各標志性氣體濃度的變化對煤自燃溫度進行預測分析，實現準確預測煤自然發火程度的目標[3-5]。為此，科研工作者開展了大量的試驗研究，利用不同機器學習算法研究分析煤自然發火標志性氣體濃度與煤自燃溫度之間的變化規律。

PAN Ke等[6]借助RBF神經網絡學習方法對自然發火標志性氣體濃度與煤自燃溫度二者的關系進行研究；鄧軍等[7]針對目前預測采空區遺煤自然發火標志性氣體種類多，且各氣體之間關系復雜，存在非線性關系，通過對支持向量機(SVM)進行改進，并與主成分分析理論(PCA)相結合，構建預測采空區遺煤自然發火程度模型，開始預測煤自燃溫度，試驗結果證明：通過PCA降維改造后的SVM預測精確度明顯提高。

RBF神經網絡方法在預測煤自燃過程中很容易進入局部最優，形成復雜的網絡結構；SVM核函數因受限于Mercer條件，在選擇參數方面非常敏感[8]，因此常規的機器學習算法預測煤自燃溫度過程中會產生較大誤差。

綜上所述，本次研究將根據極大似然估計、貝葉斯等，引進相關向量機[9-10](RVM)預測模型對煤自燃程度進行分析，結合標志性氣體濃度預測煤自然發火溫度。

1 相關向量機RVM回歸

RVM回歸指利用超參數引入，同時將權值向量假設為零，達到高斯先驗分布，實現模型的稀疏特點[11-12]，通過最大邊緣似然方法來估計超參數[13]。輸入模型具體見式(1)。

(1)

式中：xi為訓練集第i組的輸入向量；S為訓練集樣本的數量；RD為D維的實數域。

t定義為由訓練樣本輸出值ti結合而成的目標向量t=[t1,t2,…,ti,…,ts]T，其中ti表示訓練樣本第i個輸出值，i=1,2,…,S。

輸入與輸出相關向量機(RVM)回歸關系見式(2)、(3)：

ti=y(w,xi)+εi

(2)

(3)

式中：w為由S+1維權值wj結合而成的向量，其中j=0,1,…,S，則w=[w0,w1,…,wi,…,ws]T；

εi為第i個噪聲誤差，εi：N(0,δ2)，N(·)表示高斯分布，δ2表示噪聲方差；

y(w,xi)為通過權值計算得到的輸出值；

x為通過xi結合而成的矩陣，x=[x1,x2,…,xi,…,xs]T；

k(x,xi)表示由核函數k(xn,xi)結合而成的核向量，k(x,xi)=k(x1,xi)，k(x2,xi)，…，k(xi,xi)，…,k(xS,xi)，n=1,2,…,S。

在訓練樣本輸出值ti各自獨立的條件下，訓練樣本通過極大似然函數表示，具體見式(4)：

(4)

式中：φ為由核函數k(xn,xi)結合而成的核矩陣，φ=[φ(x1),φ(x2),…,φ(xn),…,φ(xs)]T,φ(xn)=[1,k(xn,x1),k(xn,x2),…,k(xn,xi),…,k(xn,xS)]。

假如直接通過最大似然方法求解向量w與高斯噪聲方差δ2，那么可能發生“過擬合”問題，將w賦予為零均值、超參數為α先驗分布，具體見式(5)：

(5)

式中：α為S+1維超參數向量，α=[α0,α1…,αj,…,αs]T。

根據馬爾科夫性質[14]得到，x*(測試輸入矩陣)相對應的y*(預測值)概率表達式，具體見式(6)：

(6)

式中：P(w,α,δ2|t)=P(w|t,α,δ2)P(α,δ2|t)。

因P(α,δ2|t)∝P(t|α,δ2)P(α)P(δ2)，“∝”為成比例關系，那么目標向量t的條件分布，具體見式(7)：

(7)

式中：Ω為目標向量t條件分布協方差，Ω=δ2I+φA-1φT，其中對角陣A=diag(α0,α1,…,αj,…,αS)，I為單位陣。

P(y*|t)的等價形式可用式(8)表示：

(8)

y*=μTφ(x*)

(9)

(10)

式中：μ為w后驗分布均值，μ=δ-2QφTt；(x*)為由測試樣本結合而成核矩陣；Q為w后驗分布協方差Q=(δ-2φTφ+A)-1。

2 RVM預測煤自燃方法

圖1為采用RVM預測煤自燃的流程，大致可分為6步。

圖1 RVM預測煤自燃流程圖

1) 井下取一部分氣體，測定氣體濃度和煤自燃時的溫度。構建訓練集(x,t)以及測試集(x*,y*)，x表示訓練集的輸入矩陣、x*表示測試集的輸入矩陣；將數據集合元素屬性輸入，具體輸入數據為C(O2)、C(N2)、C(CO)、C(CO2)、C(CH4)、O(CO/CO2)及Vmax，C(·)表示采集氣體的濃度，O(a/b)表示2種氣體a、b的濃度比值，Vmax表示預測煤自燃期間的溫度，主要由兩部分組成：測試集的預測溫度y*和訓練集的測量溫度t。

2) 建立xi(訓練集輸入向量)的高斯核函數，具體見式(11)：

(11)

式中：xn為訓練集中第n組的輸入向量；xi為訓練集中第i組輸入向量；λ表示高斯核函數的寬度。

建立高斯核函數主要是為實現訓練集的輸入矩陣x從低維空間向高維空間映射，達到更好的訓練效果[15-16]。

3) 對超參數α與噪聲方差δ2進行初始化，之后開始迭代計算，具體見式(12)、(13)。

(12)

(13)

4) 迭代完成條件達到之后，一部分αj開始接近無窮大，相對應的wi等于0；剩下的αj則開始接近有限值，相對應的xj定義為相關向量；訓練結束之后，即可獲得w和δ2的最佳值。

(14)

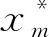
φ*=[φ*(x1),φ*(x2),…,φ*(xn),…,φ*(xs)]T

(15)

(16)

6) 通過訓練集獲得w和δ2的最優RVM模型，在模型中代入測試集和測試核矩陣，最終計算獲得煤自燃期間的預測溫度值y*及預測方差δ*2。

3 現場試驗

3.1 獲取數據

利用煤自燃模擬試驗裝置檢驗RVM在煤自燃預測過程中的準確性，試驗地點選在晉能控股集團四老溝煤礦，因該礦使用放頂煤開采，采空區遺煤較多，存在遺煤自然發火的危險。為防止采空區遺煤自然發火，設計一種相似于四老溝煤礦井下遺煤供氧與蓄熱環境的裝置，驗證煤自然發火階段各指標氣體濃度與溫度的變化規律。

通過設計的煤自燃試驗裝置——XK型煤自燃試驗裝置開展試驗。此裝置主要包括4個部分：氣路、爐體、檢測和控制，具體如圖2所示。爐體形狀為圓桶型，內徑為0.12 m，裝煤最大高度達到0.15 m，最大裝煤量為1.5 kg；通過在爐體周圍設置保溫層以及控溫水層來確保爐內煤樣擁有穩定的蓄熱條件，進氣預熱紫銅管與電熱管子安設在水層內，取氣管安設在爐中心軸處。在爐體上下安裝氣流緩沖層，保證氣流能夠均勻穿過煤體，通過控溫水層加熱的空氣，其溫度能達到煤自燃時溫度，可營造一個模擬煤自燃時的環境，之后由爐體底部進入爐內。同時在爐內不同位置安設氣體采樣點和測溫探頭。借助SP3430型號的氣相色譜儀采集和分析氣體，此色譜儀包括3部分：自動取樣機、雙柱箱、色譜數據處理工作站，具體如圖3所示。

圖2 試驗裝置

圖3 氣相色譜儀裝置

借助SP3430型氣相色譜儀分析四老溝煤礦的煤自燃特征氣體的成分和濃度，結果見表1，挑選30組數據作為訓練集，余下的8組數據為測試集。

表1 四老溝煤礦的煤自燃樣本數據

3.2 構建模型

構建3種煤自燃預測模型：RBF神經網絡、SVM和RVM，3種模型參數設置見表2。

表2 模型參數設置

RVM模型預測煤自燃的實施流程：

1) 對超參數向量α及方差δ2進行初始化處理，同時對最大迭代次數進行設置。

2) 對最大值α進行設置，在RVM迭代階段，若α大于此最大值時，就判斷其接近無窮大，與其相對應的w則為零，那么不再更新該部分值；對方差閾值進行設置，如果其方差的相對誤差比閾值小時，就判斷完成訓練要求，循環結束，退出即可。

3) 通過迭代323次之后，此次試驗訓練數據基本滿足精度要求，其中存在16個αj接近有限值，與其對應的wj不為零，獲得RVM模型的最優參數。

4) 利用已訓練的模型計算測試樣本數據，對工作面采空區煤自燃過程的溫度進行預測，同時將其和測量值進行比較分析。

3.3 結果分析

圖4為3種方法的預測溫度值與測試集真實溫度值的對比情況。采用RVM方法預測煤自燃的結果圍繞實際值上下浮動，預測精度整體相對較高；采用SVM方法預測煤自燃的精度比RVM方法差一點；采用RBF方法預測煤自燃的結果與真實值相差較大，所預測精度較低，未達到預期效果。

圖4 預測結果

圖5為3種預測方法的相對誤差，其預測相對誤差均小于20%，其中RVM預測煤自燃方法的所有樣本的相對誤差都在10%以下，且體現為集中分布及誤差值較小，SVM、RBF預測煤自燃的方法分別存在2個樣本的相對誤差超過10%.

表3為3種預測方法的平均相對誤差。這3種預測方法中，SVM和RBF預測煤自燃的方法所得到的訓練誤差值相對較低，而得到的測試誤差值較高，證明此兩種方法具有明顯的“過擬合”現象，泛化能力較低；RVM預測煤自燃的方法所得到的測試誤差值和訓練誤差值二者差值較小，具有最大的預測精度。所以RVM預測煤自燃的效果比傳統方法(RBF和SVM預測煤自燃方法)要好很多。

圖5 預測相對誤差

表3 平均相對誤差

4 結 語

以四老溝煤礦煤樣為研究對象，模擬煤自燃規律，對自燃階段所產生的特征氣體及濃度、自燃溫度進行分析。根據相關理論建立RVM煤自燃預測模型，同時和SVM、RBF模型對比。試驗結果證明：SVM、RBF具有“過擬合”問題，泛化能力不高；而采用RVM預測煤自燃的方法泛化能力強、預測精度高、模型更稀疏、預測誤差小等優勢。