基于數據驅動模型融合的鋰離子電池多時間尺度狀態聯合估計方法*

王 萍，彭香園，程 澤，張吉昂

（天津大學電氣自動化與信息工程學院，天津 300072）

前言

鋰離子電池具有自放電小、能量密度高、循環壽命長等優點，在電動汽車領域受到廣泛重視。為保障電池的安全和最佳使用，有必要配備電池管理系統（battery management system，BMS）。其中準確的狀態估計是BMS的關鍵環節，包括荷電狀態（SOC）、健康狀態（SOH）和剩余使用壽命（RUL）。這3個狀態參數從不同方面保障電池長期平穩運行，但均無法由傳感器直接測得。

SOC定義為剩余容量占其最大可用容量的比值，屬于微觀尺度的變化。安時積分法由于其簡單和易于實現在BMS中得到了廣泛的應用，但初始SOC難以獲得，且作為一種開環方法存在誤差累積的問題。開路電壓（open circuit voltage，OCV）法常與安時積分法結合用于初始SOC的校準，但需要電池的長時間靜置，不適合在線使用。相比之下，基于等效電路模型（ECM）的方法由于其自校正能力、魯棒性強以及精度高的優點得到了廣泛關注。該類方法主要利用一組狀態方程并結合濾波算法進行閉環SOC估計，常用的濾波算法有卡爾曼濾波（Kalman filtering，KF）、H濾波（Hfilter，HIF）和粒子濾波（particle filter，PF）等。但ECM的參數受工作環境以及自身狀態變化的影響，有必要為模型參數辨識以及SOC估計設計一個聯合估計框架以實現較高的估計精度和魯棒性。

現有針對兩者的聯合估計方法相當有限，大致分為兩類。第一類將模型參數和OCV合并為一個向量，用遞推最小二乘（recursive least squares，RLS）或者KF法進行聯合估計，隨后由OCV-SOC關系獲得SOC值，優點是只需要一個自適應濾波器即可獲得所有所需參數，缺點是若電池模型不準確，則會出現SOC估計不穩定甚至發散現象。第二類方法用并行濾波器以一種閉環的方式同時估計參數和SOC，因此有較高的精度。但上述兩種方法并沒有解決對SOC估計同樣至關重要的容量更新問題。

容量可以用來定量評估電池老化程度，一般用當前最大可用容量和初始容量之間的比值定義電池的另一個重要的狀態參數SOH。容量包含在基于ECM的濾波算法的計算中，因此容量的準確和實時更新對SOC估計至關重要。文獻［10］和文獻［11］中分別采用雙非線性預測濾波（dual nonlinear predictive filter，DNPF）和雙擴展卡爾曼濾波（dual extended Kalman filter，DEKF）對容量和SOC進行聯合估計，但沒有自適應調整模型參數或者只是部分調整。Wei等采用RLS辨識模型參數，用DEKF估計容量和SOC。然而兩個濾波器采用相同的時間尺度且并行工作大大增加了計算負擔。隨著大數據以及機器學習等新興技術的發展，可以考慮用老化數據離線建立模型，避免物理建模和參數辨識問題，靈活性較強，但該類方法的精度和可靠性高度依賴于與SOH相關的健康特征（HF）的選擇。

RUL（remaining useful life，RUL）通常定義為到壽命終止（end of life，EOL）時電池的剩余充放電循環周期數，用于衡量電池在其生命周期的可靠度，是宏觀尺度下對電池未來狀態的描述，而SOH屬于宏觀尺度下對當前狀態的描述。為了全面評價電池的老化程度，須同時進行SOH估計和RUL預測。然而，目前對于SOC-SOH的聯合估計較為常見，RUL預測通常單獨進行。例如文獻［16］中提出一種指數和多項式相結合的組合模型法，并用PF對模型參數在線更新，實現RUL預測。這類模型法較為簡單，但通常只能提供點預測結果，在RUL長期預測中表現不佳。此外，使用機器學習的數據驅動法也被廣泛應用于RUL預測中。Wang等將能量效率和平均工作溫度作為SVM輸入，電池當前容量和該循環周期容量的下降值為輸出，建立了多步容量預測模型。機器學習算法可以對非線性系統精準建模，但其多步迭代預測的能力較差，通常只能進行單步預測。單一方法很難實現RUL的精準預測，融合算法是目前的研究方向，此外，RUL是對未來的狀態進行描述，需要提供預測結果的不確定性表達，以提升預測的可靠性。

綜上所述，上述研究存在以下問題：一是SOC、SOH和RUL三者之間存在著耦合和步驟重疊的問題，單獨估計不能保證精度同時也增加了計算量，例如SOC估計必不可少的前提是電池容量和模型參數的實時校準，RUL長期預測的前提是對當前SOH的精準可靠估計。二是電池參數、SOH和RUL隨時間變化緩慢，而SOC隨時間變化迅速，因此使用相同的時間尺度不能得到準確可靠的估計值，且大大增加了控制系統的計算量，降低穩定性。

為此，本文中提出一種基于模型數據驅動融合的鋰離子電池多時間尺度狀態聯合估計方法。首先建立戴維南模型，采用最小二乘（least square，LS）辨識阻容參數，提取內阻作為HF，建立LSSVM電池老化模型，實現SOH估計；利用GPR對內阻隨循環次數的變化進行映射，預測內阻的變化趨勢，并結合LSSVM模型實現RUL預測。用阻容參數辨識值和SOH估計值更新狀態空間方程，采用UKF算法實現放電階段的SOC估計。在牛津數據集中進行驗證，結果表明所提方法具有較高精度和魯棒性。

1 在線參數辨識和健康特征提取

本文選取牛津數據集，標記為Cell1～Cell 8。數據集的詳細介紹請參照文獻［21］。

1.1 戴維南等效電路模型

考慮到計算量和精度，本文建立1階戴維南等效電路模型，如圖1所示。

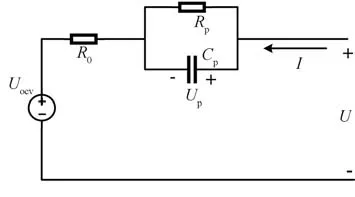
圖1 戴維南等效電路模型

其中：I表示輸入電流；U為端電壓；R為歐姆內阻；R和C分別表示極化電阻和極化電容；U為開路電壓，與SOC相關，即U=f(SOC)，一般在實驗室環境下通過小電流充放電獲取，然后采用多項式擬合。由于一次U測試耗時較長，且文獻［22］中指出f受電池老化的影響較小，在全生命周期內變化不大，故這里選用新電池的U-SOC曲線。

根據基爾霍夫電壓電流定律，可得

1.2 在線參數辨識

考慮到模型參數隨電池老化而變化，模型參數需在線更新以提高狀態估計精度。

電池放電工況復雜多變，而充電工況一般采用恒流恒壓固定充電模式，可用于在線參數辨識。恒流充電下的SOC的表達式為

式中Q(n)表示第n次充放電循環下的可用容量，此時的健康狀態計算公式如式（3）所示，式中Q為電池的出廠容量。

結合式（1）和式（2），可得不同循環次數下恒流充電的電池端電壓的變化特性，如式（4）所示，各變量上標n表示循環次數n。

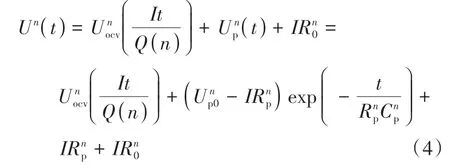
可以看出，模型參數以及容量隨循環次數的更新，屬于宏觀尺度；SOC是時變參數，屬于微觀尺度，且受到宏觀尺度參數的影響，這里也體現了多時間尺度狀態聯合估計的必要性。

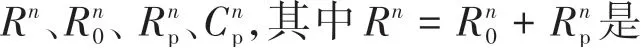
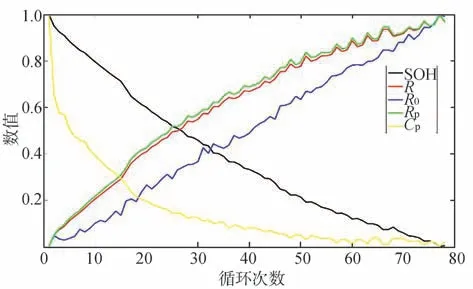
圖2 Cell1標準化阻容參數和SOH的變化趨勢

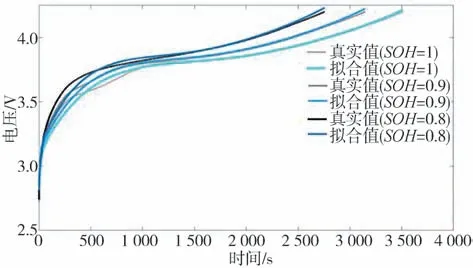
圖3 Cell1的電壓真實值和模型輸出值

1.3 相關性分析和健康特征提取

鋰離子電池的老化原因主要有3種：（1）鋰離子損失（loss of lithium inventory，LLI），（2）活性物質的損失（loss of active material，LAM），（3）電阻增加（resistance increase，RI）。LLI主要來源于固體電解質界面（solid electrolyte interphase，SEI）的形成和電解液分解引起的副反應消耗了可循環鋰；LAM直接影響電池的可用容量；RI是電極和電解質降解的結果，且LLI和LAM都會導致RI。由圖2可以看出，電阻隨循環次數的增加而增大，與老化機理一致，定性表明電阻可以反映電池老化信息。

選用Pearson相關系數和灰色關聯度（grey relation coefficient，GRC）進一步定量評價各參數與SOH的相關性：

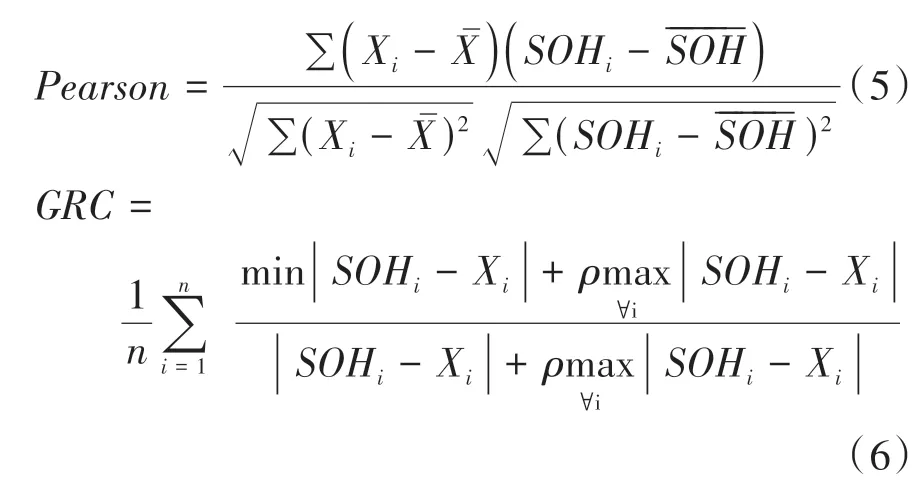
式中：X為第i次循環的阻容參數；SOH為第i次循環的SOH值；n為循環總數；ρ為分辨系數，一般取0.5。計算結果列于表1，絕對值越接近1，說明相關性越高。

從表1可以看出，R與SOH的相關性最高，Pearson系數的絕對值在0.98以上，GRC在0.9以上，與老化機理一致，故直接選取內阻R為HF。

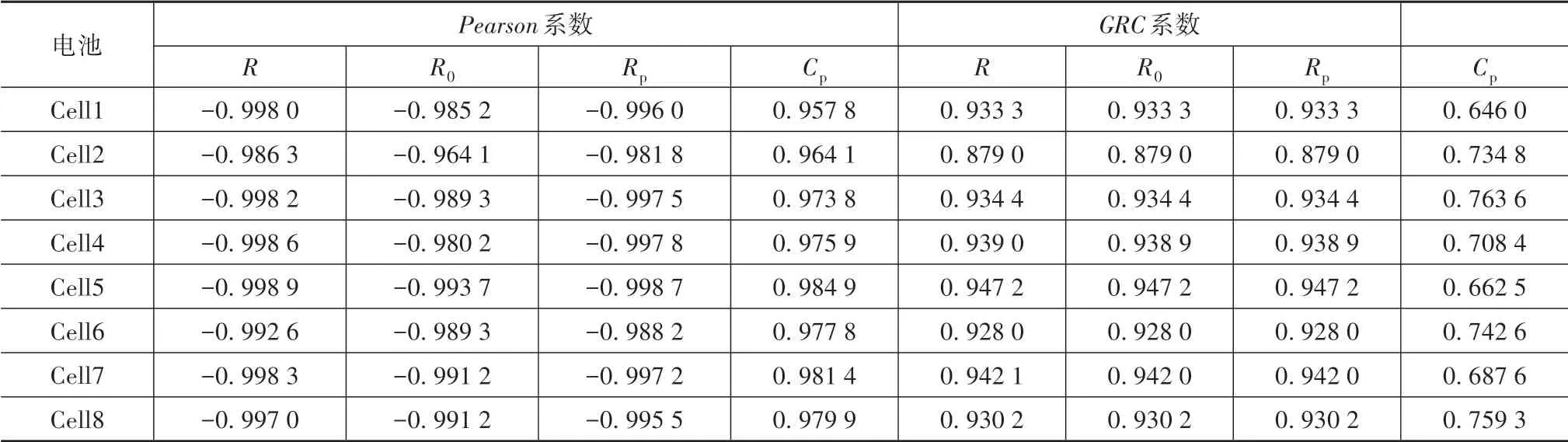
表1 阻容參數與SOH的Pearson和GRC系數

2 聯合估計方法

2.1 UKF算法

本文模型部分主要是戴維南模型結合UKF。UKF算法基于UT變換技術，與其他KF系列方法相比，避免了求導運算，對狀態方程的要求低，同時對方差的估計更為準確。

狀態量的初始值和初始誤差協方差矩陣分別為

式中：λ是Sigma點的尺度參數，λ=α(n+κ)-n，α描述Sigma點偏離狀態值的程度，滿足10≤α≤1，κ是副尺度參數，為保證方差半正定，滿足κ≥0，一般在狀態估計時取0，在參數估計時取3-n；β是一個與Sigma點分布相關的量，當Sigma點成高斯分布時，通常β=2。

（2）預測階段

采樣時刻k，Sigma點構建的矩陣為

2.2 LSSVM算法

2.3 GPR算法

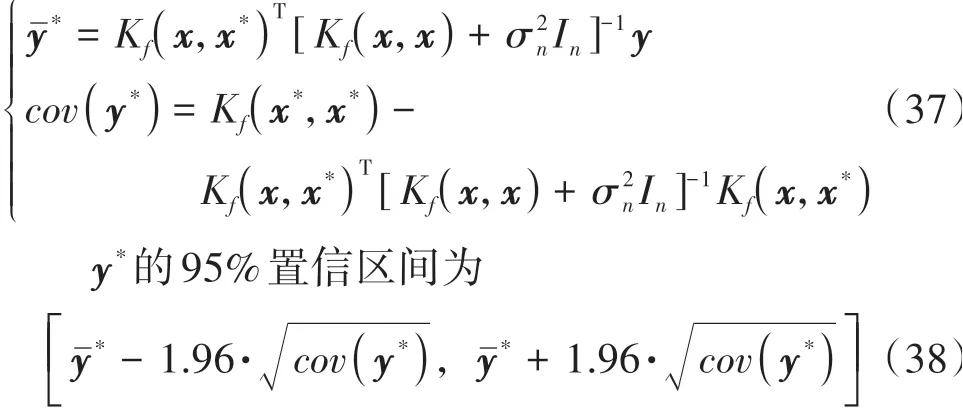
2.4 SOC-SOH-RUL聯合估計框架

為提高估計精度，減少計算量，本文中提出一種鋰離子電池多時間尺度狀態聯合估計框架，用微觀尺度估計SOC，用宏觀尺度估計電池參數、SOH并進行RUL預測。整體流程圖如圖4所示。

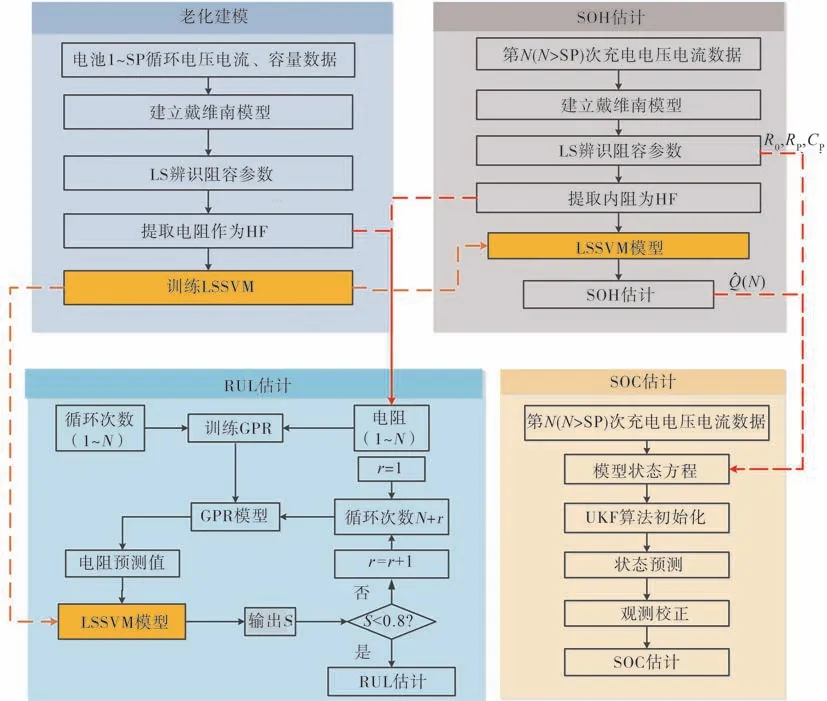
圖4 鋰離子電池SOC-SOH-RUL聯合估計框圖

第一步：老化建模。對預測起點（starting point，SP）之前的循環周期，建立戴維南模型，采用LS算法辨識阻容參數，提取內阻作為HF，建立LSSVM電池老化模型。

第二步：SOH估計。對于第N次循環（N＞SP），辨識當前循環下的內阻值作為HF，輸入LSSVM老化模型中進行SOH估計。

3 聯合估計結果與分析

選用相對誤差百分比（relative percentage error，RPE）、平均絕對誤差（mean absolute error，MAE）以及均方根誤差（root mean squared error，RMSE）對估計結果進行定量評估，x和x^分別表示真實值和估計值：

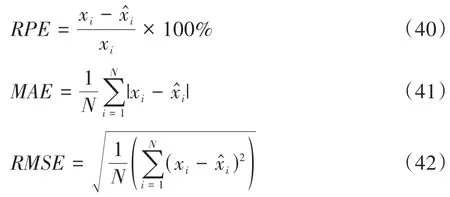
Cell1～Cell 3、Cell 7和Cell 8的標準化周期數約為80，SP設為30。Cell 4～Cell 6的標準化周期數約為50，SP設為20。電池EOL設為0.8，EOL以后的狀態估計不在本文考慮的范圍內。

3.1 SOH和RUL估計結果

以Cell 1、Cell 4為例，圖5展示了SOH估計和RUL預測結果及誤差，綠色和藍色虛線分別表示SP和EOL，可以看出SOH預測軌跡均能反映真實的衰退趨勢。所有電池誤差的MAE和RMSE列于表2，各電池SOH估計的RPE均在1%以內，MAE和RMSE在0.5%以內，驗證了本文所選HF—內阻能夠很好地表征電池的老化，并能適應電池不一致性帶來的容量衰退趨勢差異。同時表明LSSVM算法具有較強的非線性映射能力，在數據量較小的樣本（Cell 4～Cell 6）中也能實現SOH的準確估計。

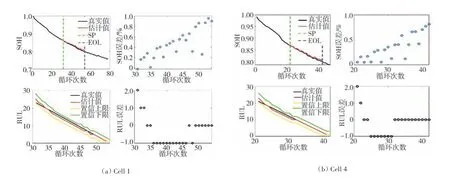
圖5 SOH估計和RUL預測結果以及誤差

此外由圖5可知，各周期RUL預測值（紅線）與真實值（黑線）非常接近，最大誤差為2，且持續周期數較少。而且可以發現，越接近EOL，RUL預測效果越好，預測誤差均為0個周期，這在實際行駛中是非常有意義的，因為越接近EOL，越需要RUL的精準預測值，以及時發現電池的異常狀態，降低風險并提高電池的可維護性。綠線和黃線分別表示RUL置信區間的上下限，估計值和真實值都落在置信區間里，且置信區間的寬度較窄，表明估計結果具有較高的可靠性。SP取值分別是20和30，表明即便在數據量很小情況下，GPR算法也能夠通過循環次數外推預測HF的變化趨勢，并結合LSSVM模型對容量衰退趨勢進行預測，實現RUL預測。以Cell 7為例，圖6和圖7分別展示了不同循環次數下對內阻和SOH衰退趨勢預測的結果，由圖可知外推值雖然不能完全刻畫特征和容量的波動，但是能夠很好地跟隨內阻和SOH衰退的實際趨勢，從而保證了RUL預測的準確性。表2定量給出了所有電池的RUL預測誤差，各電池MAE均小于1，RMSE最大值為1.172 6，表明所提方法具有較高的精度和穩定性。

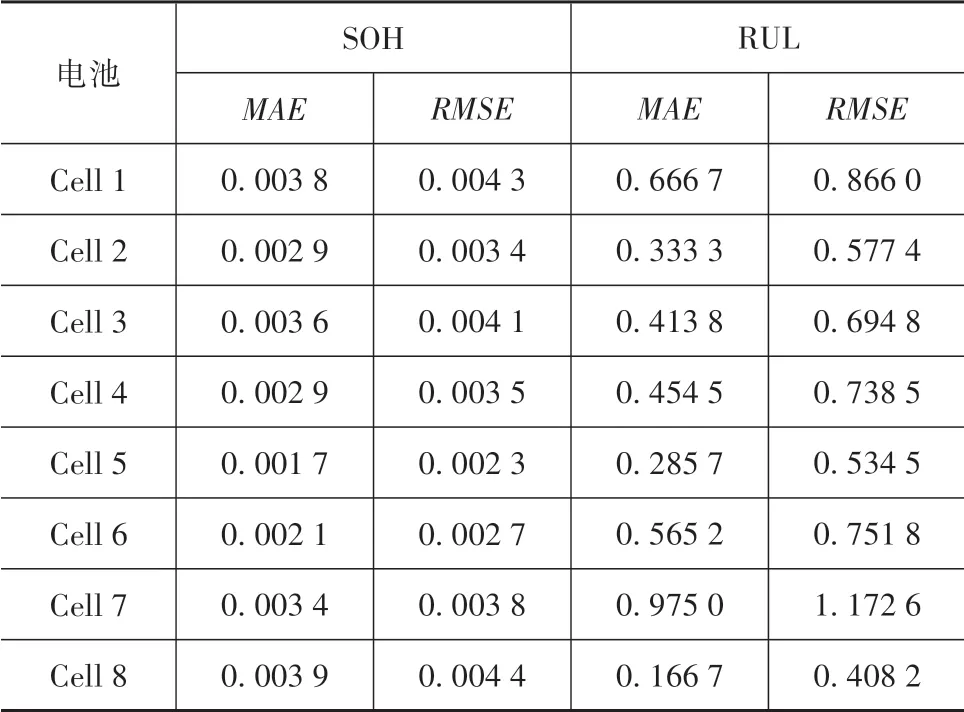
表2 SOH和RUL估計誤差

圖6 Cell 7的內阻趨勢預測

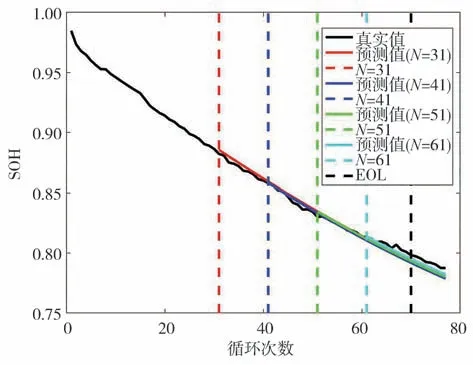
圖7 Cell 7的SOH衰退趨勢預測

3.2 SOC估計結果

圖8 展示了各電池SOC估計結果。實際中SOC初值通常難以獲得，為驗證算法的魯棒性，設置SOC的初始誤差為0.5。定義跟隨時間為SOC估計值與真實值的誤差小于0.1的時間和放電總時間的比值，計算跟隨時間之后的MAE和RMSE，其隨循環次數的變化趨勢如圖8（a）～圖8（h）的下圖所示。從SP到EOL的總循環次數中取兩次循環，兩次循環周期的放電階段SOC估計效果如圖8（a）～圖8（h）的上、中兩張圖的紅線所示。

可以看出，SOC估計的初始誤差較高，但可以很快跟隨真實SOC曲線，不同循環次數下的跟隨時間都在0.06左右，反映了UKF算法較強的魯棒性。隨著電池接近EOL，SOC的估計誤差稍大，這樣的誤差主要來源于參數和SOH估計誤差，但整體來看，各電池各循環周期的MAE和RMSE均在3%以內，滿足誤差要求。圖8（a）～圖8（h）的上、中兩張圖的藍色曲線是SOC單獨估計的效果，即UKF的狀態和觀測方程的阻容參數設為常數，Q(n)設為額定容量，不隨電池老化自適應更新，此時SOC出現了明顯的偏離，且隨著電池老化更加嚴重。而采用本方法，阻容參數和當前容量可以隨電池老化的進行而自適應調整，因而提高了ECM的適應性，在電池全壽命周期都能取得較高的SOC估計精度。

圖8 SOC估計結果和誤差

4 結論

本文中提出了一種基于等效電路模型和數據驅動融合的鋰離子電池多時間尺度狀態聯合估計方法。主要工作如下：

（1）建立戴維南模型，每個循環周期下，對充電電壓曲線采用LS辨識阻容參數；

（2）直接提取ECM內阻作為HF，該HF能表征電池老化機理，減少了額外提取HF的計算量，建立LSSVM電池老化模型實現SOH估計；

（3）利用模型參數辨識值和SOH估計值自適應更新狀態方程矩陣參數，采用UKF算法實現放電階段SOC估計；

（4）采用GPR對內阻隨循環次數的變化趨勢進行建模，通過循環次數的外推實現內阻變化趨勢預測，結合LSSVM老化模型實現RUL預測；

（5）在牛津數據集的8個電池上進行實驗驗證，結果表明所提方法能夠實現多時間尺度狀態的準確、魯棒估計。

下一步將在其他類型電池以及更為復雜工況下進行驗證。