復(fù)合材料火箭筒體的力學響應(yīng)分析及建模方法研究

張 淼，隋 欣，黨海燕，王寧飛

(1 北京理工大學宇航學院，北京 100081；2 北京特種機械研究所，北京 100143)

0 引言

復(fù)合材料具有良好的性能，使其在工程領(lǐng)域得到了廣泛的應(yīng)用。將復(fù)合材料應(yīng)用于火箭筒體,可減輕質(zhì)量，滿足隱身、防彈等軍事要求，提升火箭武器系統(tǒng)戰(zhàn)術(shù)技術(shù)性能。近年來，隨著復(fù)合材料在火箭筒體上的大量使用，如何更有效研究復(fù)合材料筒體的力學性能和變形特性對于火箭筒體設(shè)計優(yōu)化有著重要的意義。在進行筒體研究時，其建模計算仿真是必不可少的步驟，建模方法的正確選擇對于后續(xù)工作影響深遠，因此筒體建模方法的研究十分必要。

文中基于有限元數(shù)值仿真的方法，以有限元計算軟件ABAQUS為開發(fā)平臺，分別采用實體-殼單元綁定與全部殼單元兩種方法建立兩種復(fù)合材料筒體的仿真模型，將仿真結(jié)果與試驗數(shù)據(jù)進行了對比，結(jié)果表明，研究筒體強度時選擇實體-殼單元綁定的方法建模獲得的結(jié)果更貼合實際試驗結(jié)果。

1 復(fù)合材料層合板理論及其非線性模型

1.1 理想層合板基本假設(shè)

根據(jù)力學相關(guān)理論，做以下假設(shè)：

1)層合板變形很小，且材料服從胡克定律；2)層與層之間理想粘接，無間隙，無粘接層厚度，無錯動，且沿厚度方向變形連續(xù)；3)層合板中變形前垂直于中面的直線段，變形后仍保持直線且垂直于中面。

1.2 單層板任意方向上的應(yīng)力應(yīng)變方程

如圖1所示，單層板任意方向上的應(yīng)力應(yīng)變關(guān)系滿足：

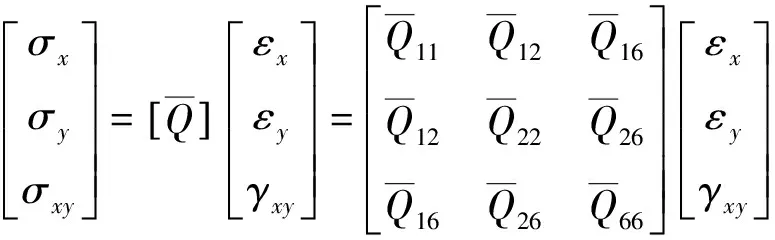
(1)

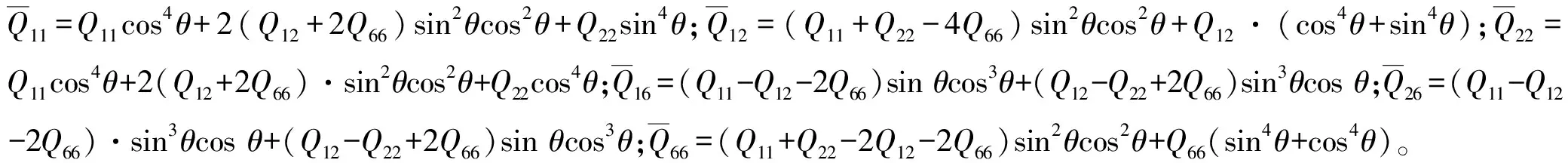
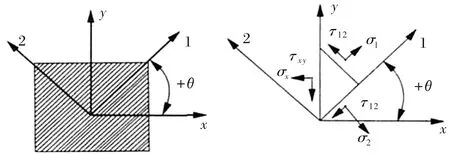
圖1 單層板任意方向上的應(yīng)力應(yīng)變關(guān)系

1.3 經(jīng)典層合板非線性本構(gòu)方程

如圖2所示，由各單層板應(yīng)力沿厚度方向積分，可得到層合板單位寬度內(nèi)力和內(nèi)力矩方程為：

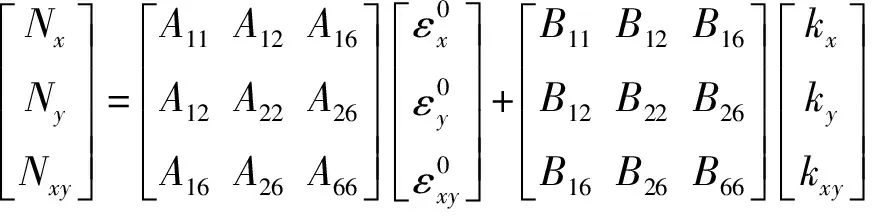
(2)

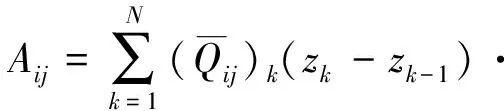
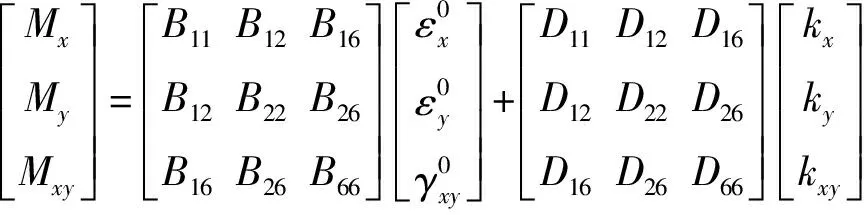
(3)

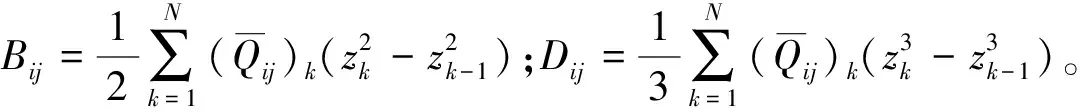
以上分析構(gòu)成了復(fù)合材料經(jīng)典層合板理論及其非線性數(shù)學模型。

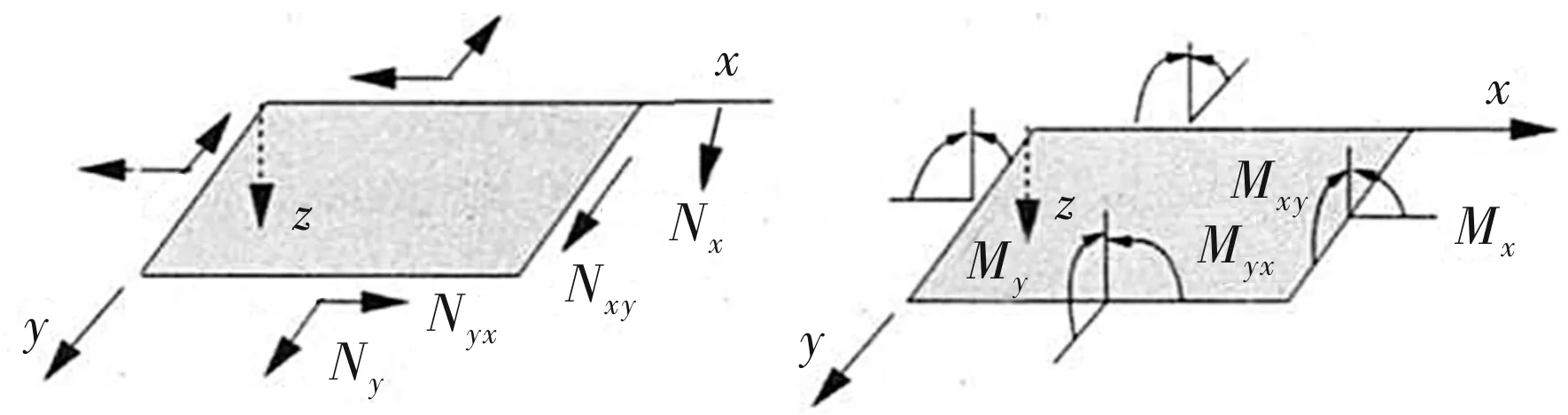
圖2 層合板內(nèi)力、內(nèi)力矩

2 有限元仿真模型

2.1 筒體模型及計算假設(shè)

模型為復(fù)合材料筒體，三維結(jié)構(gòu)如圖3。

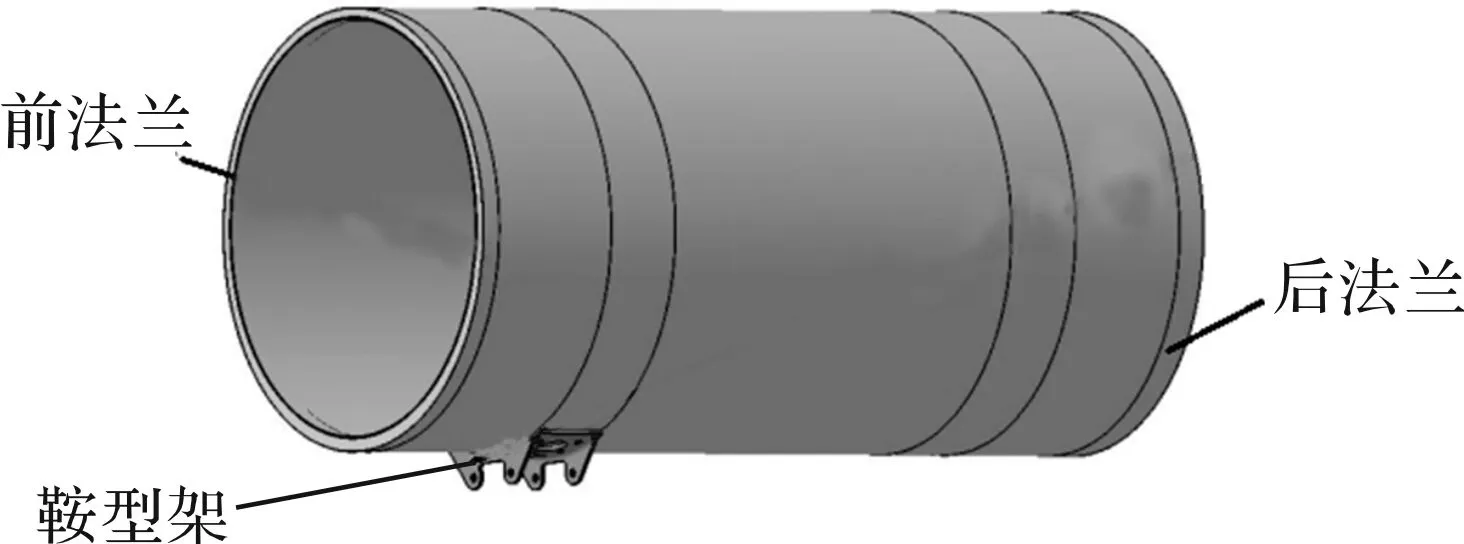
圖3 筒體模型

根據(jù)筒體模型，分別建立兩種有限元仿真模型。筒的結(jié)構(gòu)尺寸完全相同，筒體長度為5 000 mm，內(nèi)徑為1 000 mm，最大外徑為1 100 mm，筒體包括內(nèi)結(jié)構(gòu)層、保溫層和外結(jié)構(gòu)層，內(nèi)結(jié)構(gòu)層為復(fù)合材料筒體，保溫層為泡沫，外結(jié)構(gòu)層為PE層和外蒙皮。

第一種建模方法：分別建立殼單元的內(nèi)結(jié)構(gòu)層、PE層和外蒙皮，實體單元的泡沫層。由于各部件之間是層層鋪疊、緊密貼合的，故將內(nèi)結(jié)構(gòu)層與泡沫層、泡沫層與PE層、PE層與外蒙皮之間的相互作用都設(shè)置為綁定約束，建立的有限元仿真模型如圖4(a)。其中，內(nèi)結(jié)構(gòu)層與泡沫層的綁定約束中內(nèi)結(jié)構(gòu)層為主表面，泡沫層為從表面；泡沫層與PE層的綁定約束中泡沫層為主表面，PE層為從表面；PE層與外蒙皮的綁定約束中PE層為主表面，外蒙皮為從表面。內(nèi)結(jié)構(gòu)層、PE層與外蒙皮的網(wǎng)格類型為S4R，泡沫層的網(wǎng)格類型為C3D10，網(wǎng)格數(shù)量為23 967。

第二種建模方法：直接建立殼單元筒體，內(nèi)結(jié)構(gòu)層、泡沫層、PE層與外蒙皮在同一部件上，在內(nèi)結(jié)構(gòu)層的基礎(chǔ)上增加泡沫層、PE層與外蒙皮，建立的有限元仿真模型如圖4(b)。網(wǎng)格類型為S4R，網(wǎng)格數(shù)量為2 970。

建模軟件中實體單元和殼單元的薄厚顯示存在差異，實體單元顯示厚度而殼單元只顯示殼體。

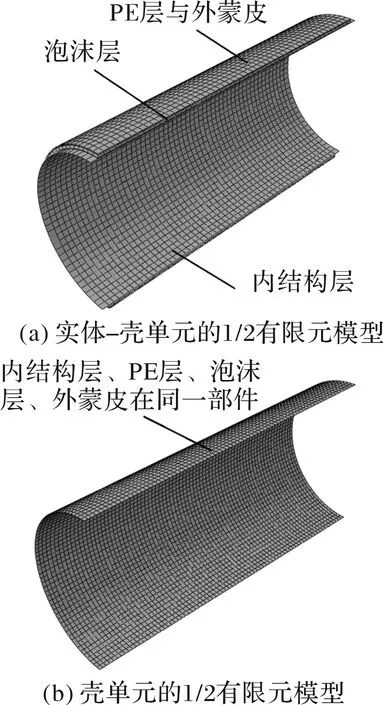
圖4 有限元模型

為了便于計算，文中假設(shè)火箭為普通剛體。

2.2 材料參數(shù)

筒體結(jié)構(gòu)材料主要是T300碳纖維、玻璃纖維、PE纖維和泡沫，各個材料體系的力學性能參數(shù)如表1～表2所示。

結(jié)構(gòu)部分由材料以0°/90°兩個角度為一周期交替纏繞，每個周期的材料厚度相同。

表1 泡沫的物性參數(shù)

表2 復(fù)合材料的力學參數(shù)

2.3 邊界條件與載荷

工況1(發(fā)射工況)：筒體內(nèi)施加0.8 MPa的內(nèi)壓載荷，筒體前后法蘭端面及鞍型架與筒體接觸面位置設(shè)置固定約束。

工況2(起豎工況)：筒段水平放置，在鞍型架位置通過工裝施加集中壓力載荷，大小為700 kN，載荷方向垂直于筒體軸向方向向上，筒體前后法蘭端面及鞍型架與筒體接觸面位置設(shè)置固定約束。

3 有限元結(jié)果分析

3.1 筒體變形分析

對于工況1，兩種模型的筒體位移云圖如圖5。

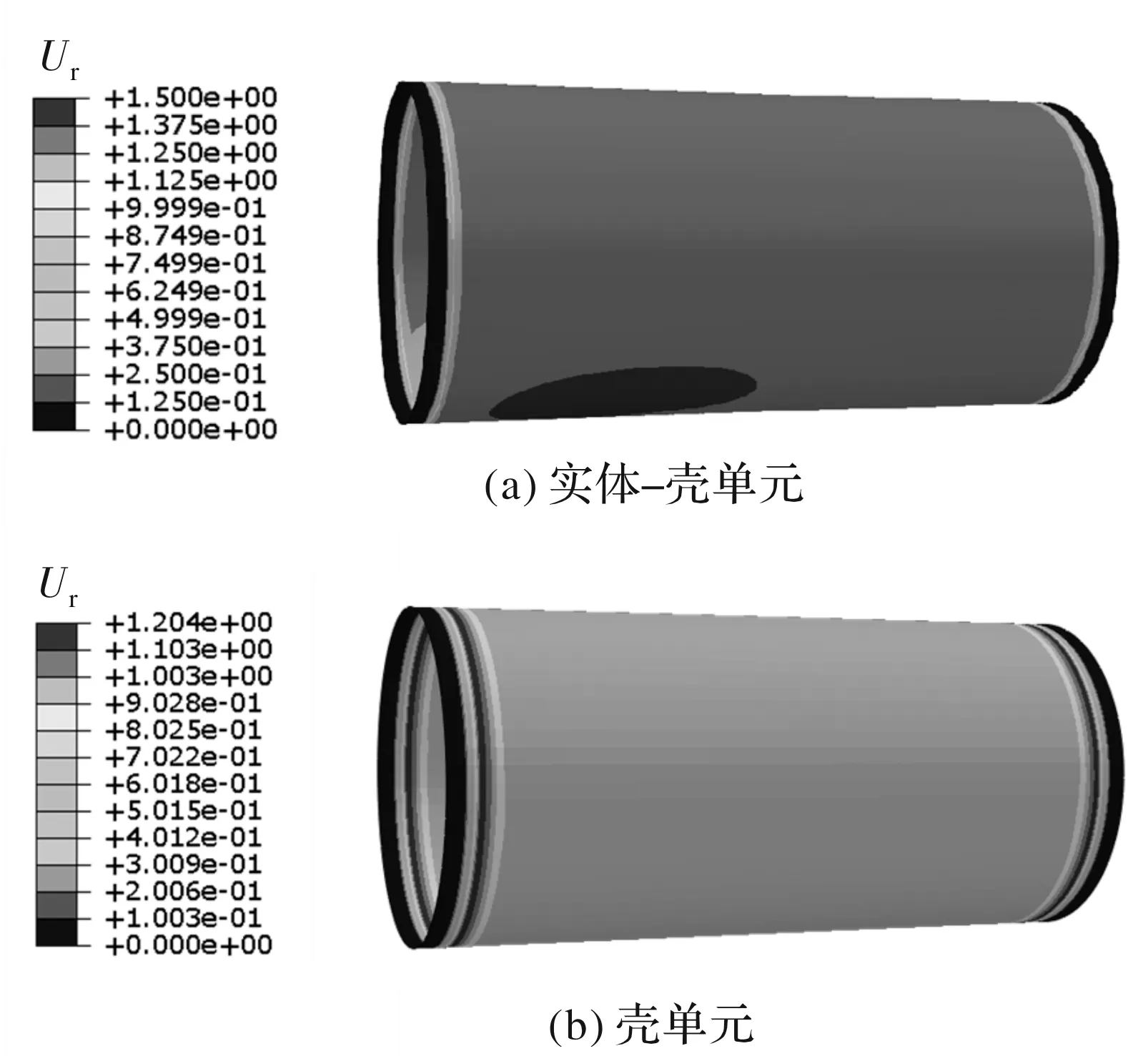
圖5 工況1兩種模型筒體的位移云圖

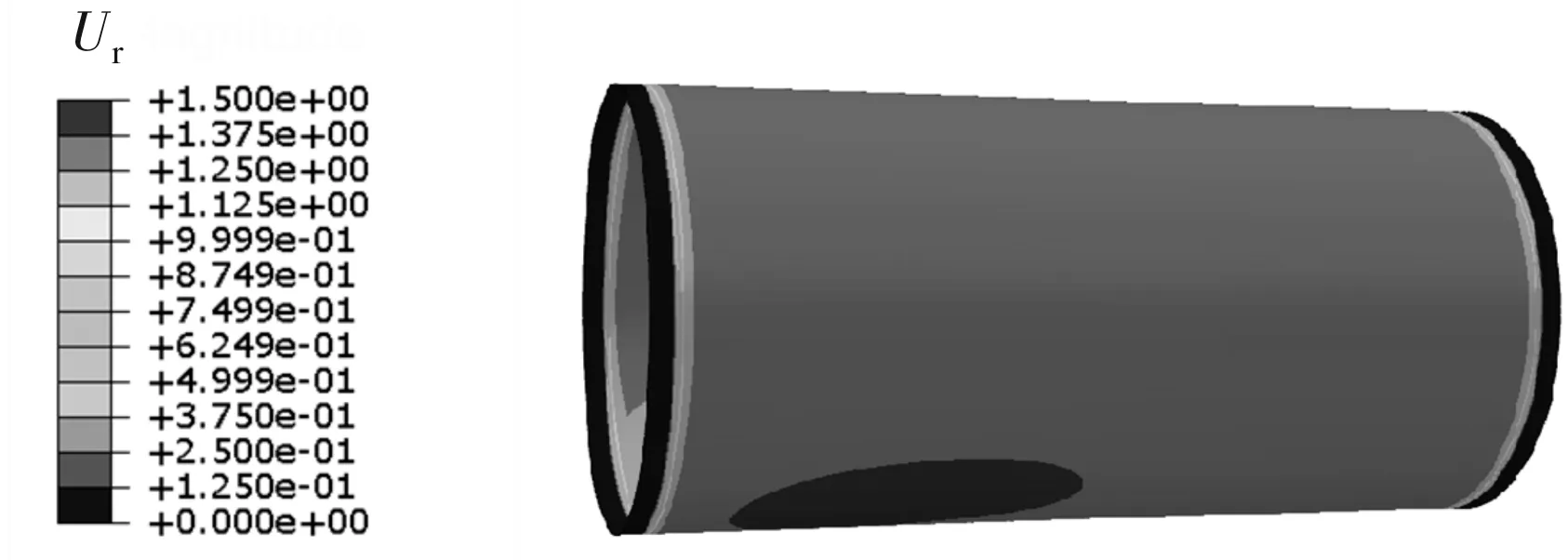
圖6 工況1實體-殼單元模型中內(nèi)結(jié)構(gòu)層的位移云圖

該工況下，實體-殼單元模型的最大變形位置在筒體下方中部，出現(xiàn)最大變形的部件為內(nèi)結(jié)構(gòu)層，云圖如圖6所示，殼單元模型的最大變形位置在前后法蘭內(nèi)側(cè)。這種變形結(jié)果是由于筒體前后法蘭都被完全固定，筒體中部位置離被固定位置最遠，受力大從而變形最大，而內(nèi)部加壓筒體會產(chǎn)生變形，前后法蘭內(nèi)側(cè)由于同時受到被固定位置的約束力和內(nèi)部壓強，導(dǎo)致此部分變形較大。

兩種模型中最大變形出現(xiàn)的位置完全不同，這是因為：首先兩種模型使用的單元不同，實體-殼單元模型中使用了兩種單元，可以更真實模擬筒體內(nèi)部單元之間以及各部件之間的力學響應(yīng)，即實體單元泡沫層對殼單元內(nèi)結(jié)構(gòu)層的影響，而殼單元模型只使用了一種單元，且各部分建立在一個部件上，忽略了不同種類單元以及各部分之間的接觸對力學響應(yīng)的影響；其次各部分的材料屬性不同，實體-殼單元模型中盡管用綁定約束各個部件，但受到較大壓強時各部件的剛度差異較大，各個差異疊加后反映在仿真結(jié)果的差異更大，而殼單元模型中各部分建立在一個部件上，相對削弱了各部分之間的差異，因此利用兩種模型計算后的仿真結(jié)果存在不同。

對比兩種模型的變形云圖，實體-殼單元模型的最大變形量為1.5 mm；殼單元模型的最大變形量為1.2 mm。

對于工況2,兩種模型的筒體位移云圖如圖7。

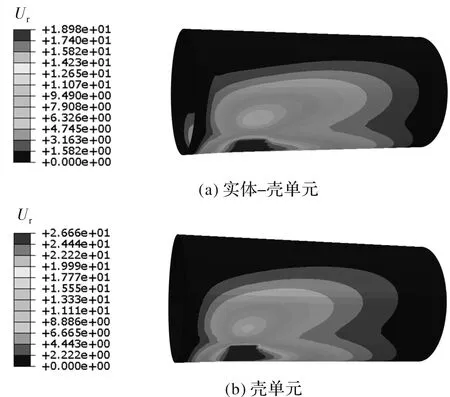
圖7 工況2兩種模型筒體的位移云圖

該工況下，鞍型架兩側(cè)變形量最大，這是因為鞍型架與筒體接觸面固定，同時在鞍型架下側(cè)施加載荷，導(dǎo)致鞍型架兩側(cè)變形最大。對比兩種模型的位移云圖，實體-殼單元模型的云圖后側(cè)變化梯度相對較小，變形相對均勻，最大變形出現(xiàn)在PE層，云圖如圖8所示，變形量為18.98 mm；殼單元模型的筒體整體變形較大，且云圖后側(cè)變化梯度相對較大，最大變形量為26.6 mm。

圖8 工況2實體-殼單元模型中PE層的位移云圖

3.2 應(yīng)力分析

對于工況1，兩種模型的筒體應(yīng)力云圖如圖9。

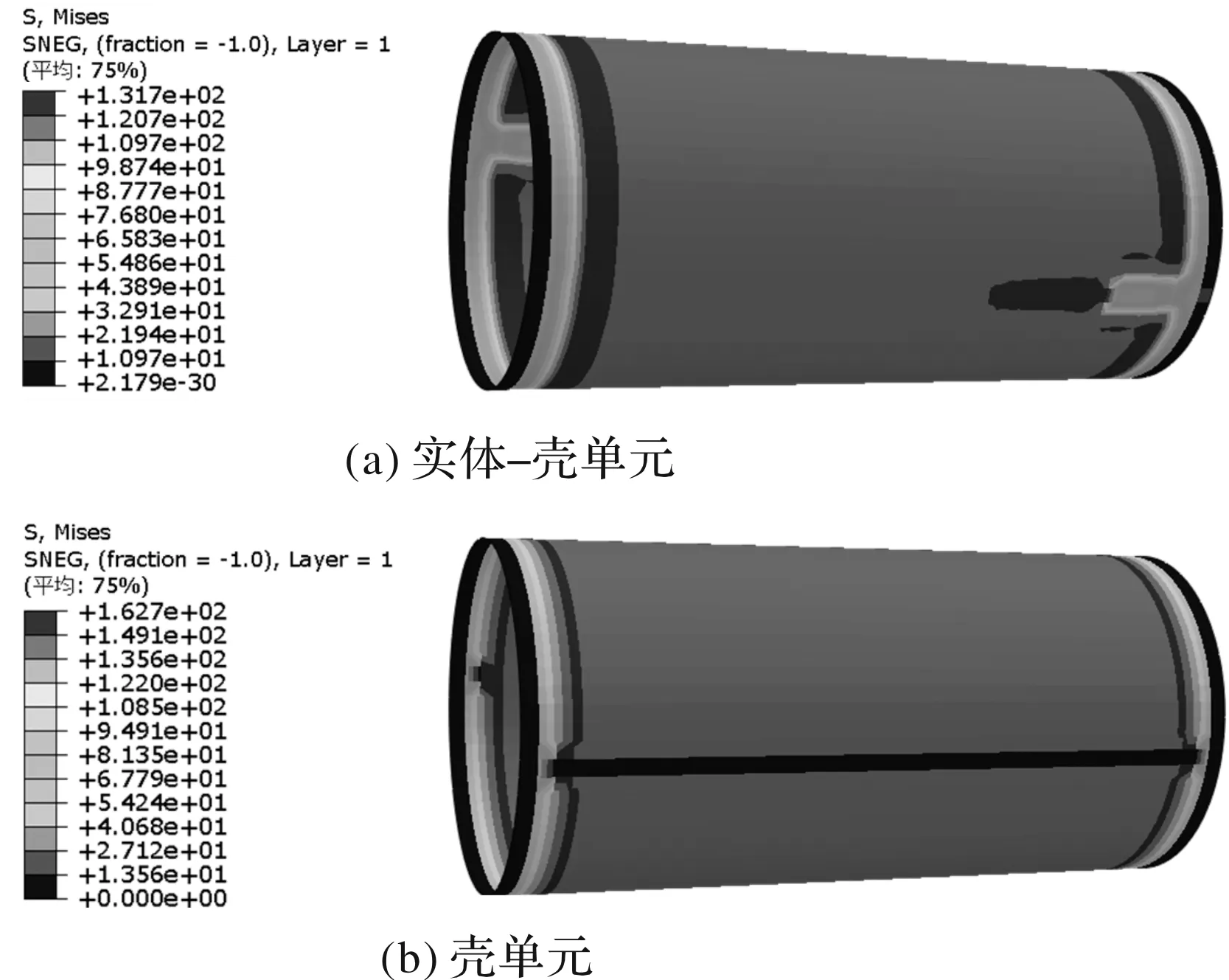
圖9 工況1兩種模型筒體Von Mises等效應(yīng)力云圖

該工況下，兩種模型的應(yīng)力最大位置均在后法蘭前側(cè)，這是由于此位置受力較大，但受力面積因變形減小，從而導(dǎo)致應(yīng)力最大。實體-殼單元模型的最大應(yīng)力出現(xiàn)在內(nèi)結(jié)構(gòu)層如圖10，最大應(yīng)力為162.7 MPa；殼單元模型的最大應(yīng)力為131.7 MPa。

圖10 工況1實體-殼單元模型內(nèi)結(jié)構(gòu)層的Von Mises等效應(yīng)力云圖

對于工況2，兩種模型的筒體應(yīng)力云圖如圖11。

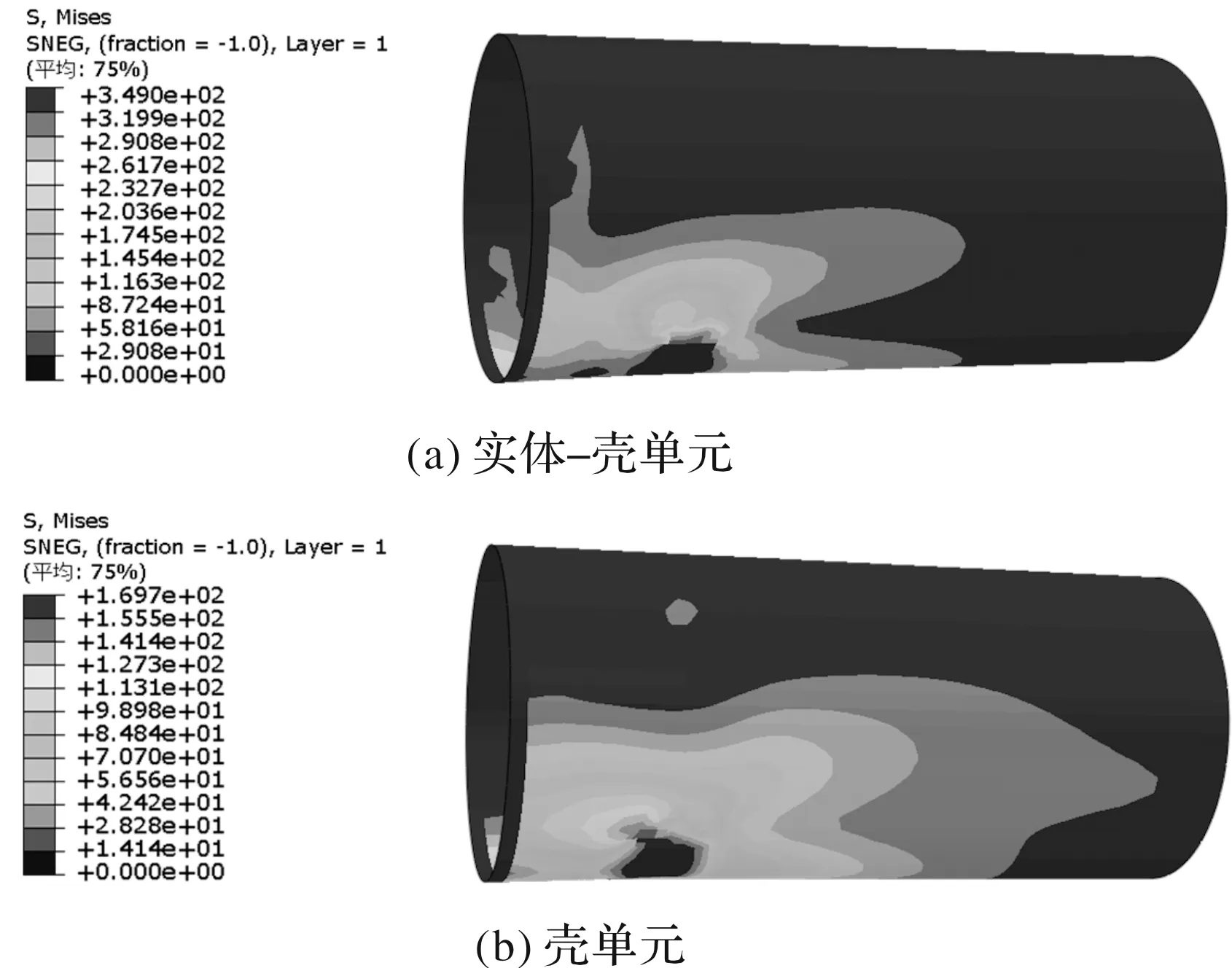
圖11 工況2兩種模型筒體Von Mises等效應(yīng)力云圖

該工況下，兩種模型的應(yīng)力最大位置均在鞍型架兩側(cè)，這是由于鞍型架兩側(cè)受力最大，同時變形量大導(dǎo)致面積減小，從而應(yīng)力變大。如圖12,實體-殼單元模型的最大應(yīng)力出現(xiàn)在PE層為349 MPa；殼單元模型的最大應(yīng)力為169.7 MPa。

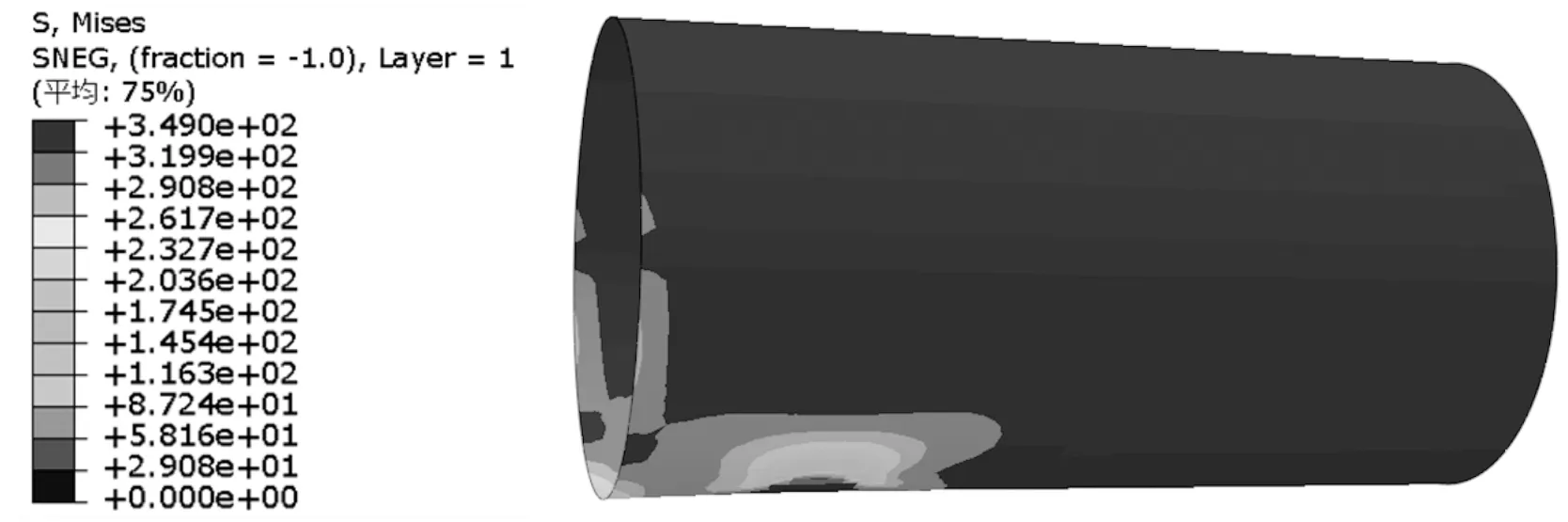
圖12 工況2實體-殼單元模型PE層的Von Mises等效應(yīng)力云圖

3.3 應(yīng)變分析

對于工況1，兩種模型的筒體應(yīng)變云圖如圖13。

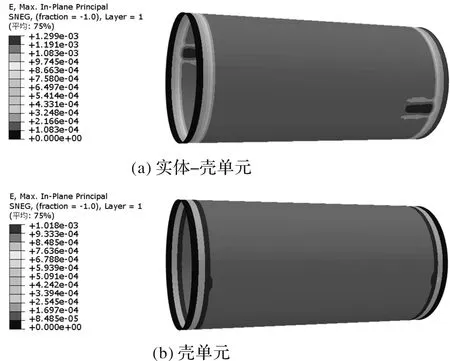
圖13 工況1兩種模型筒體應(yīng)變云圖

該工況下，兩種模型的應(yīng)變最大位置均在后法蘭前側(cè)，這是由于此部分變形較大從而導(dǎo)致應(yīng)變變大。實體-殼單元模型的最大應(yīng)變出現(xiàn)在內(nèi)結(jié)構(gòu)層如圖14，為0.129 9%；殼單元模型的應(yīng)變云圖更為均勻，最大應(yīng)變?yōu)?.101 8%。

圖14 工況1實體-殼單元模型內(nèi)結(jié)構(gòu)層的應(yīng)變云圖

對于工況2，兩種模型的筒體應(yīng)變云圖如圖15。

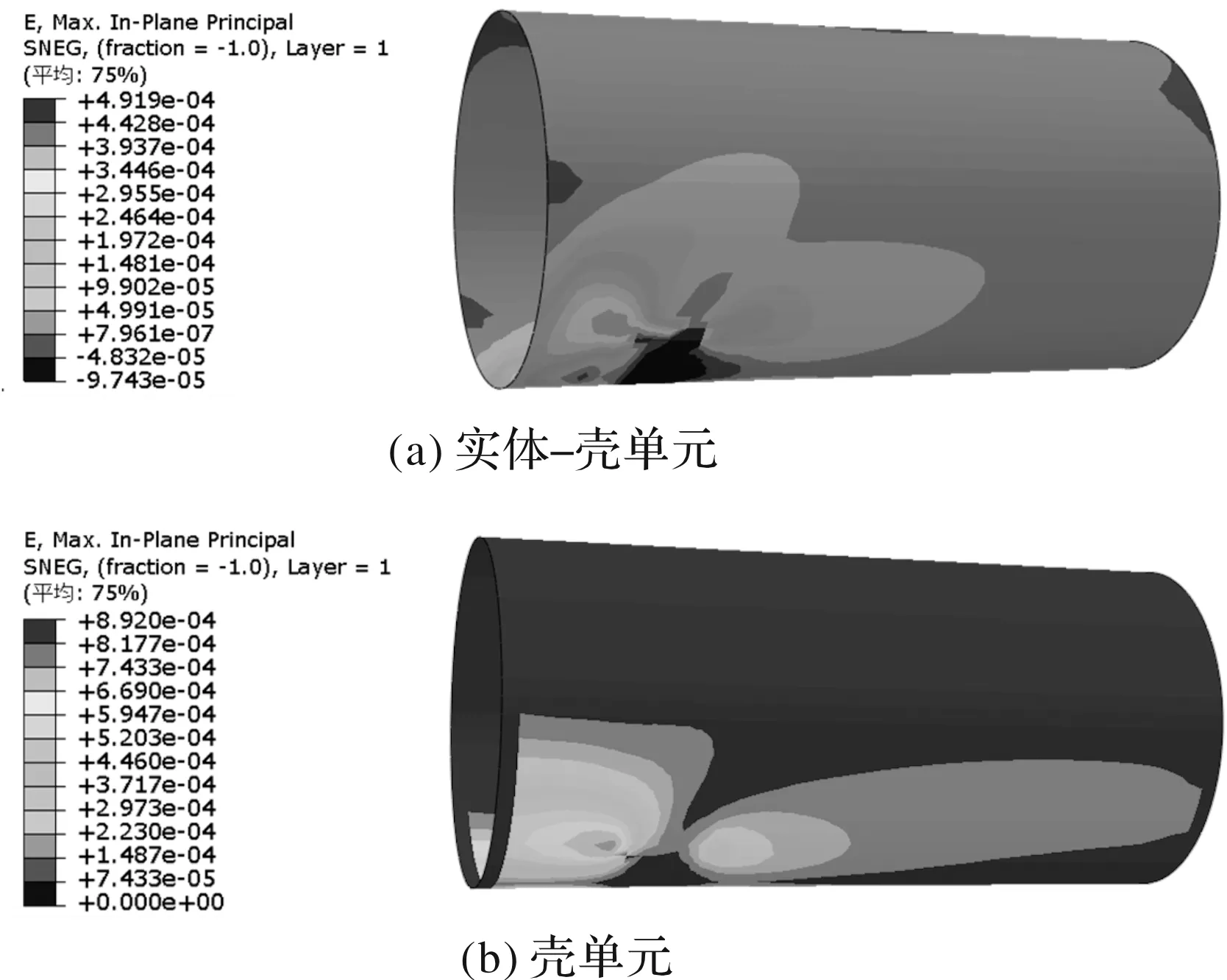
圖15 工況2兩種模型筒體應(yīng)變云圖

該工況下，實體-殼單元模型的最大應(yīng)變位置在鞍型架右側(cè)，為0.049 19%，最大應(yīng)變出現(xiàn)在內(nèi)結(jié)構(gòu)層，云圖如圖16；殼單元模型的最大應(yīng)變在鞍型架前側(cè)，為0.089 2%。這是由于鞍型架周圍的受力最大，變形最大，導(dǎo)致此部分應(yīng)變最大。

圖16 工況2實體-殼單元模型內(nèi)結(jié)構(gòu)層的應(yīng)變云圖

4 試驗及結(jié)果分析

4.1 工況1結(jié)果分析

用內(nèi)壓試驗來模擬筒段的發(fā)射工況。在筒體前部、中部、后部分別周向均勻布置3組應(yīng)變傳感器，每組8個如圖17所示；在鞍型架位置及筒體中部均勻布置2組位移傳感器，每組4個，后部布置2個位移傳感器，共10個如圖18所示。向筒段內(nèi)部灌滿水，并加水壓，逐步加載至內(nèi)壓達到0.8 MPa，在內(nèi)壓為0.2 MPa,0.4 MPa,0.6 MPa,0.8 MPa時分別采集對應(yīng)的應(yīng)變及位移數(shù)據(jù)。筒段內(nèi)壓試驗測試結(jié)果如表3。由試驗結(jié)果可知，在水壓達到0.8 MPa后，筒段的最大應(yīng)變在后法蘭前方右側(cè)位置，為0.137 2%，最大位移在正下方中部位置，為1.57 mm。

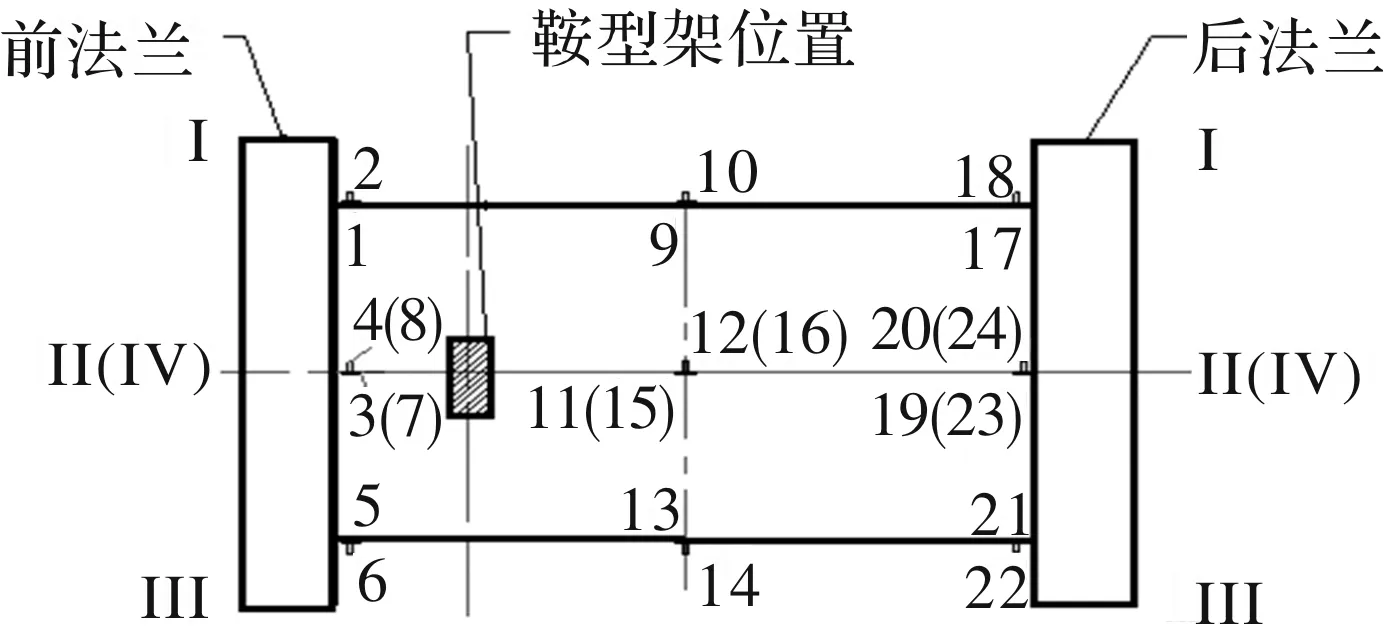
圖17 工況1試驗應(yīng)變測點示意圖

圖18 工況1試驗位移測點示意圖

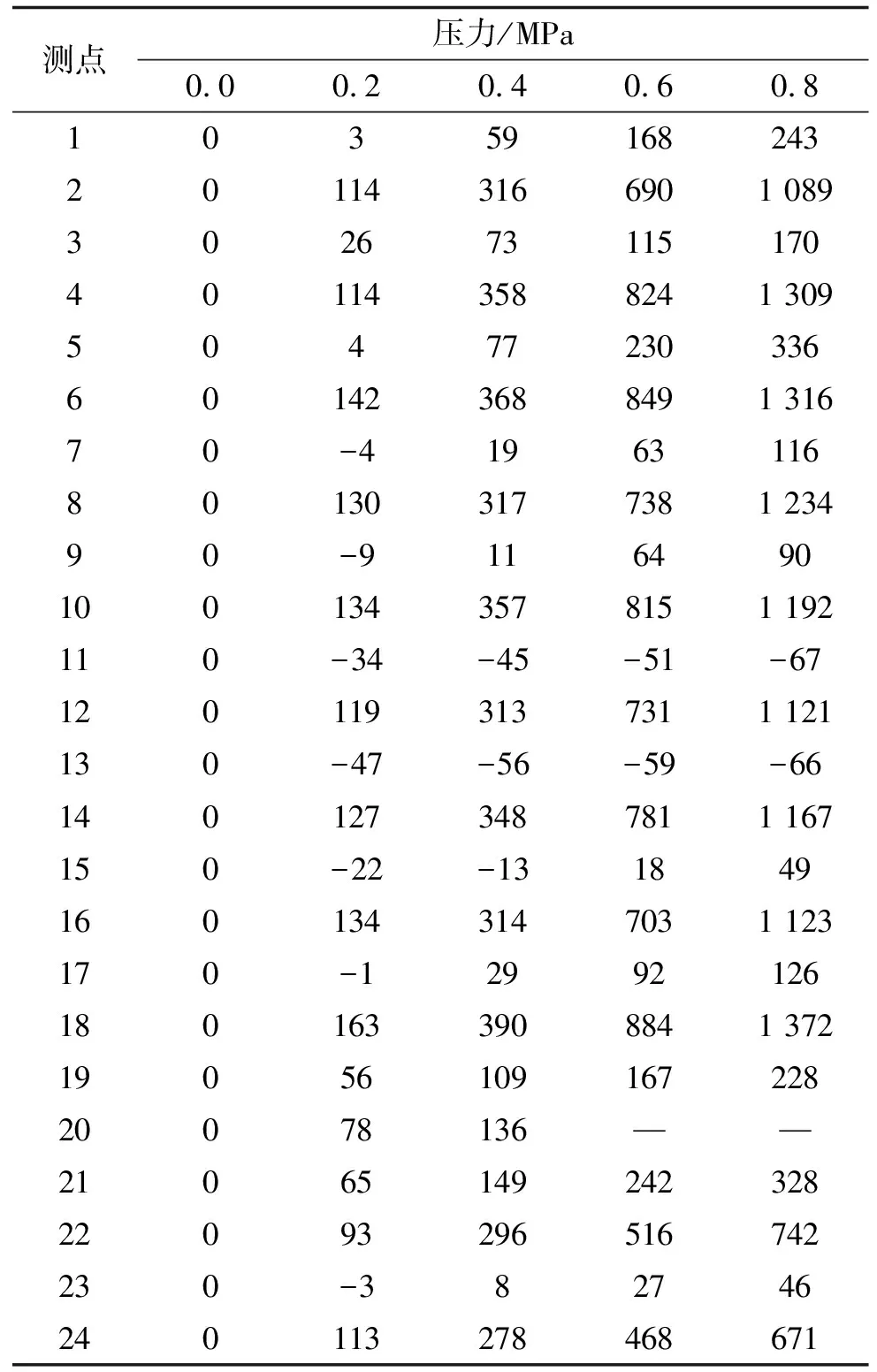
表3 內(nèi)壓試驗應(yīng)變測試結(jié)果 單位:με

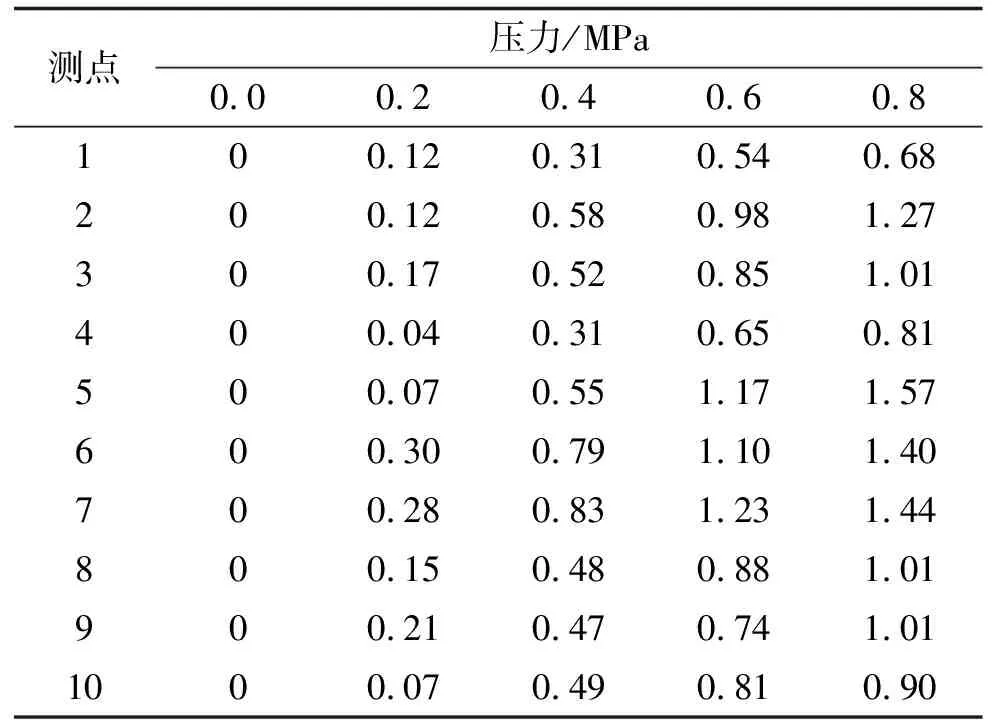
表4 內(nèi)壓試驗位移測試結(jié)果 單位:mm

4.2 工況2結(jié)果分析

用起豎試驗來模擬筒段的起豎工況。在鞍型架位置周向均布20個應(yīng)變傳感器如圖19所示；在筒體前側(cè)和鞍型架位置布置2組位移傳感器，每組3個，在筒體后側(cè)及轉(zhuǎn)接法蘭位置布置2組位移傳感器，每組4個如圖20所示。

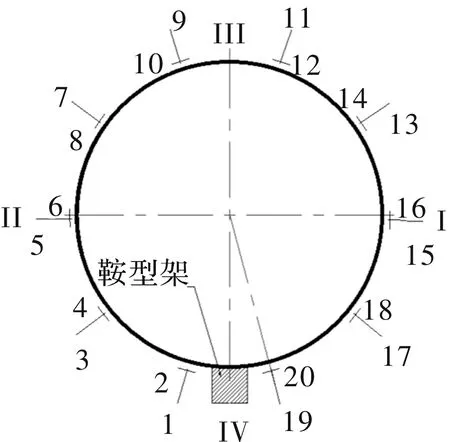
圖19 工況2試驗應(yīng)變測點示意圖

圖20 工況2試驗位移測點示意圖

對筒段慢慢進行加載，當力傳感器顯示為70 t時停止試驗，在載荷達到10 t,20 t,30 t,40 t,50 t,60 t,70 t時分別采集試驗對應(yīng)的應(yīng)變及位移數(shù)據(jù)。筒段起豎試驗測點數(shù)據(jù)結(jié)果如表5～表6。由結(jié)果可知，在加載到70 t后，筒段的最大應(yīng)變在鞍型架右側(cè)，為0.038 1%，最大位移在鞍型架前側(cè)，為20.36 mm。

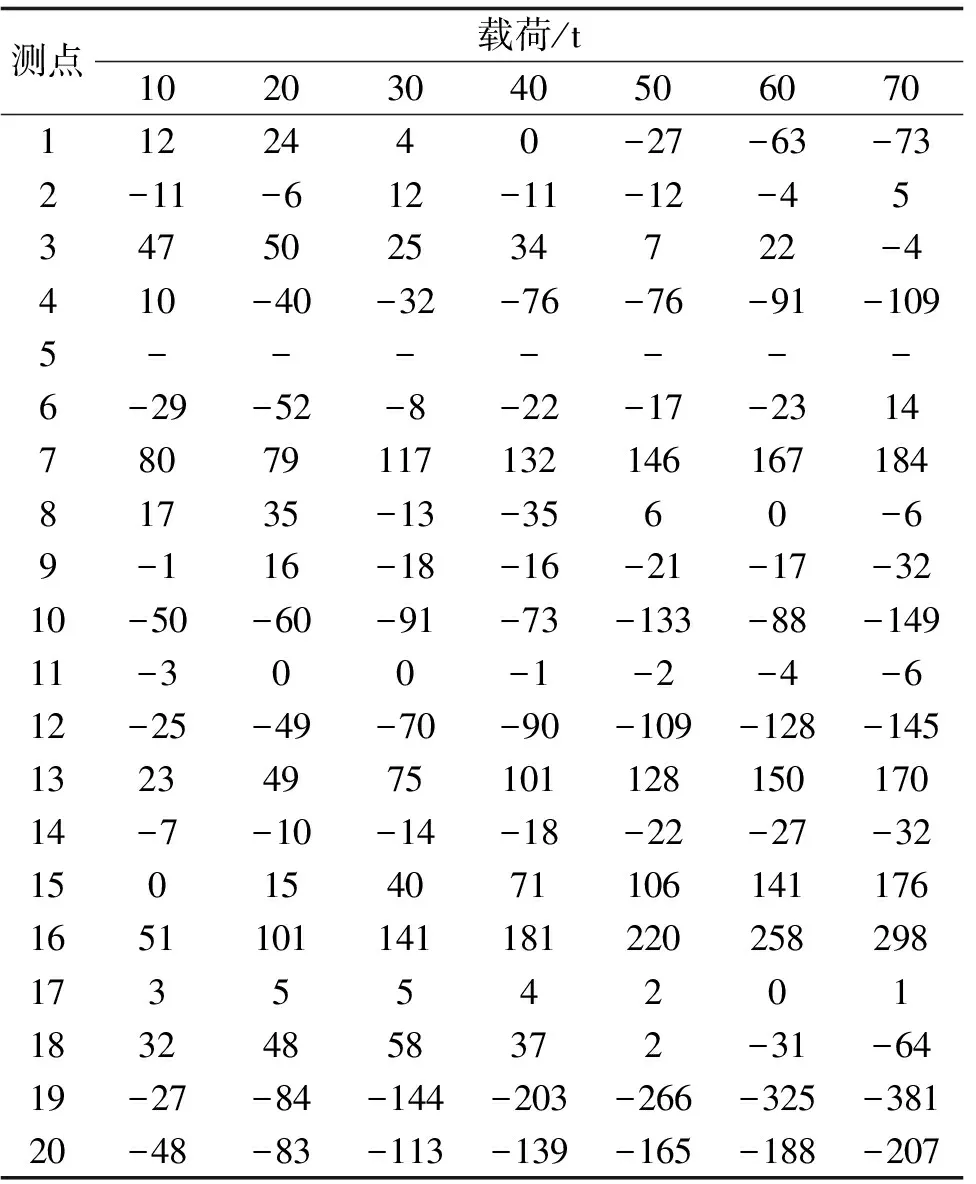
表5 起豎試驗應(yīng)變測試結(jié)果 單位:με

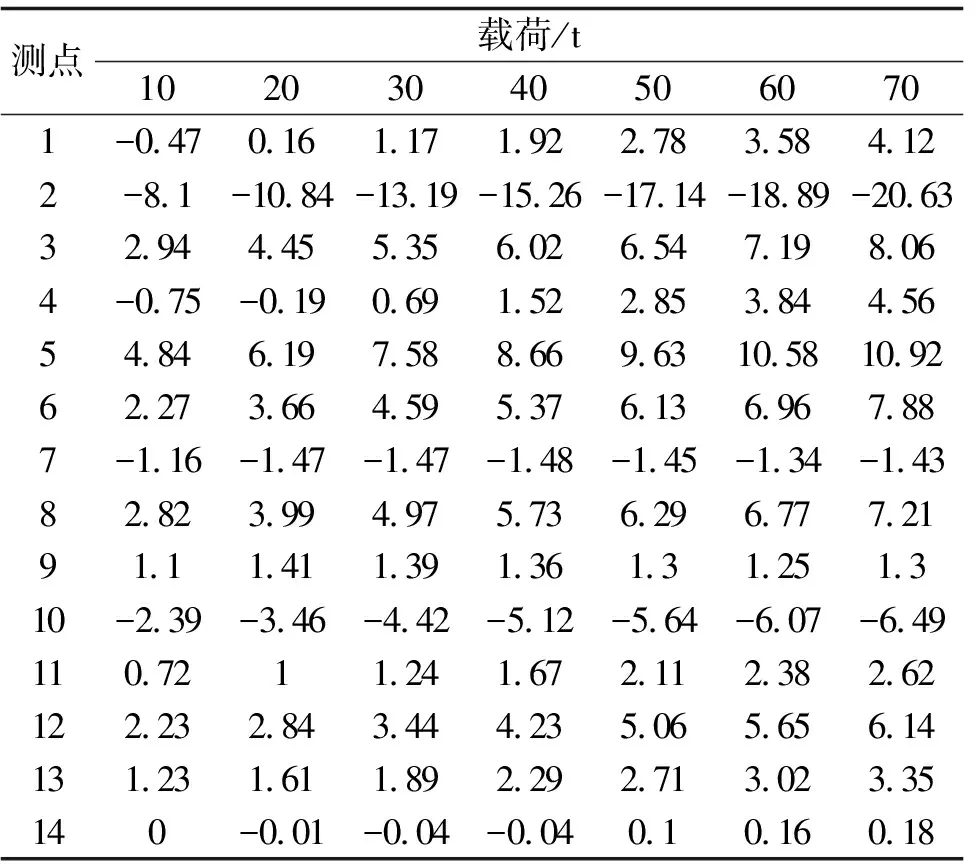
表6 起豎試驗位移測試結(jié)果 單位:mm

試驗測量結(jié)果與仿真計算結(jié)果對比見表7，可以看出，在誤差允許范圍內(nèi)，實體-殼單元的建模方法與試驗更為相符，且最大應(yīng)變出現(xiàn)的位置也更吻合，所以實體-殼單元的建模方法更具準確性。

表7 試驗測量結(jié)果與仿真結(jié)果對比

5 結(jié)論

基于有限元建模仿真軟件ABAQUS，利用不同的建模方法建立了兩種有限元模型，分別模擬了復(fù)合材料火箭筒體的發(fā)射工況和起豎工況，得到了筒體的應(yīng)力應(yīng)變和變形的數(shù)據(jù)，同時做了內(nèi)壓試驗和起豎試驗，得出以下結(jié)論：

1)發(fā)射工況下，筒體變形的最大位置在正下方中部，應(yīng)力應(yīng)變的最大位置均在后法蘭前側(cè)位置。

2)起豎工況下，筒體變形及應(yīng)力應(yīng)變的最大位置均在鞍型架附近。

3)在建立復(fù)合材料筒體的仿真模型時，選擇實體-殼單元綁定的方法建模獲得的仿真結(jié)果更貼合試驗結(jié)果。

在今后的復(fù)合材料火箭筒體設(shè)計中，應(yīng)對筒體中部及鞍型架部位適當加強，以提高筒體的力學性能；同時在仿真計算時應(yīng)盡量選用實體-殼單元綁定的建模方法，以獲得更真實的仿真結(jié)果。