天線隨機振動分析與設計優化
付佐紅,董高彬,程馳青,邵惠琳
(1. 中電防務科技有限公司,南京 210007;2. 徐州工業職業技術學院,江蘇 徐州 221140)
0 引 言
隨著飛行器朝著高速度、高機動的方向不斷發展,機上的振動環境越發嚴酷,對設備的耐振動性能要求也日益苛刻,統計表明40%的飛機事故與振動有關[1]。機載衛星天線能夠對目標衛星定向和跟蹤,建立數據傳輸鏈路,從而實現通訊[2]。為保證機載天線在振動環境下穩定可靠,避免機體振動損壞天線,本文通過降低應力集中、減少轉接件、減輕質量等方式來提高天線固有頻率、增加天線剛度,從而提高天線抗振動能力[3-4]。
1 天線概況及其安裝背景
該款天線安裝位置為直升機旋翼頂端,如圖1所示,該位置振動量級較大,加之該天線具有百兆網口和SDI視頻功能,導致功放功率、體積和重量均大幅增加,對結構件的強度、天線整機的抗振動能力提出較高要求,現行該型號機載天線無法滿足,須對天線結構進行優化設計。
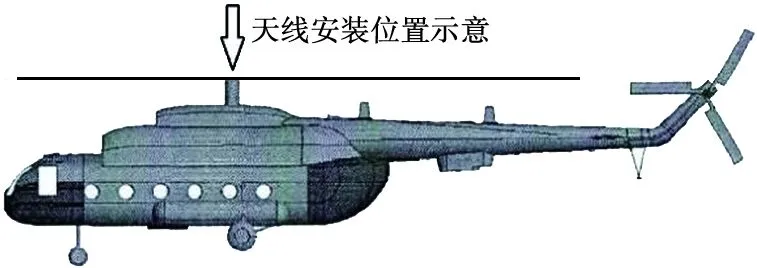
圖1 天線裝機位置示意圖
天線結構上由天線面及饋電網絡、俯仰/方位傳動機構、模塊安裝組件等部分構成,如圖2所示,天線以橫梁支架為安裝主體,變頻器、功放、電源等模塊安裝于模塊安裝板上,俯仰/方位傳動機構帶動天線面及饋電網絡的任意方向旋轉,使天線面始終正對通信衛星,從而實現所需通信功能。

圖2 天線結構框架示意圖
2 天線結構優化
2.1 減少應力集中
俯仰天線面及饋電網絡部分與俯仰傳動機構中的扇形齒輪相連接,俯仰電機驅動俯仰小齒輪,從而帶動天線面進行俯仰運動。天線面與饋電網絡部分重量通過極化網絡安裝板全部壓在左右俯仰支架上。在實際振動試驗過程中,左右俯仰支架均有不同程度的裂隙,為分析該結構受力情況,使用有限元方法對該天線進行靜應力、模態計算、隨機振動分析。
2.1.1 建立模型與前處理
本文的三維模型均在UG軟件中建立,為計算方便,簡化天線三維模型中各齒輪輪齒、螺紋,將模型導入有限元軟件ANSYS后進行網格劃分。網格設置為四面體網格,網格總數約741 000個,傳動部分網格可適當密些,天線面網格可適當稀疏,最大網格尺寸不超過3 mm。
該款機載天線振動環境為隨機振動,根據國標GJB150.16A設置振動條件如圖3所示,其中f取500 Hz,加速度譜面密度W0=0.001 g2/Hz,W1=0.01 g2/Hz。結構件材料為鋁合金LY12,天線面材料為碳纖維。設置天線下方安裝接口為固定面、振動條件施加面。

圖3 施加振普圖
2.1.2 仿真結果
由于天線安裝在天線罩內,除重力、飛機起落加速度外幾乎不受其他靜應力影響,仿真結果與實際無異,所有結構件所受應力均不會超過材料屈服強度許用值。
由于在振動試驗過程中斷裂零件為左俯仰支架,因此隨機振動仿真只關注該零件。左右俯仰支架應力云圖如圖4所示。
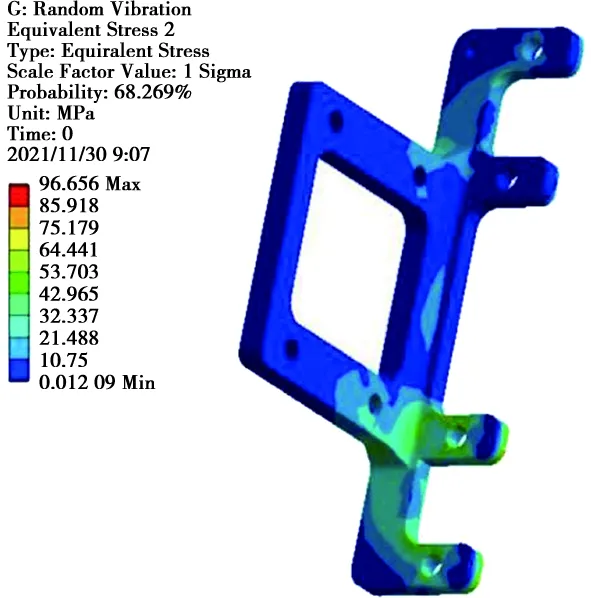
圖4 俯仰支架應力云圖
可以看出,在1σ條件下,零件根部應力最大值為96.6 MPa,則3ε條件下應力可達289.8 MPa,臨近LY12鋁合金屈服強度325 MPa。安全系數μ=2-(325/289.8)=1.12,該零件安全系數過小,在實際使用中損壞的可能性極大,因此對該零件進行優化設計。
2.1.3 正交實驗設計
本文通過正交實驗對該零件進行優化改進,圖5給出了該俯仰支架結構件優化流程。
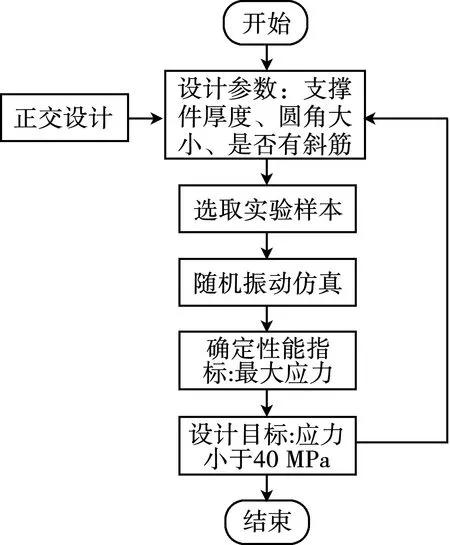
圖5 俯仰支架結構優化流程圖
本文選取該左俯仰支架厚度、斷裂處圓角大小、是否有斜筋3個參數作為因素,每個因素兩水平,正交實驗設計如下:
支架厚度A:6 mm、8 mm(分別記為A1、A2);
斷裂處圓角大小B:7 mm、10 mm(分別記為B1、B2);
是否有斜筋C:無、有(分別記為C1、C2)。
表1、表2分別為正交方案設計與正交實驗結果統計。

表1 正交方案設計

表2 有限元仿真結果統計
正交實驗得到的結果較為淺顯,還要進行更深入的計算和分析:利用實驗結果分析結構件應力、結構件重量等指標隨各因素變化的規律,以及各因素對兩個實驗指標影響輕重順序;正交實驗并不是簡單地將各因素所有水平進行了排列組合,本文僅僅做了部分實驗,不能確保各因素中的最優組合剛好在所選取的實驗組合中,須找出各因素各水平的最佳組合。
極差分析法是在正交實驗設計中較為常用的結果分析方法,計算簡單,結果直觀。本次實驗有2個指標:一是零件所受最大應力應小于鋁合金屈服強度,以保證LY12鋁合金不斷裂;二是零件重量,機載零件重量錙銖必較,在零件所受應力較小的條件下首選重量較輕的各因素的參數組合。先采用極差直觀分析法分析實驗過程中各因素對零件所受最大應力、重量這兩個單一指標的影響,綜合分析比較不同因素對各指標的影響,經取舍確定最優的各因素不同水平下的組合方案,最大應力和重量實驗結果分析分別如表3、表4所示。
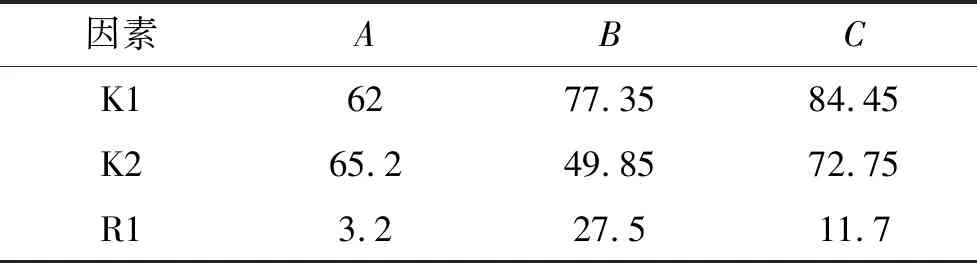
表3 正交實驗最大應力指標結果分析(單位MPa)
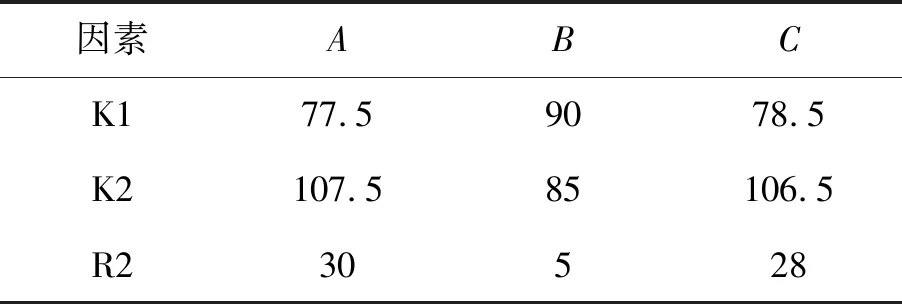
表4 正交實驗重量指標結果分析(單位g)
表中為相同指標每個因素下各水平的平均,即
(1)
定義R為該實驗中所選取的各因素極差,其意義是實驗中某一因素各水平實驗指標的最大值與最小值之差,即
R=maxKi-minKi
(2)
結合上述分析結果,最大應力極差值R1A很小,即支架厚度對優化應力集中意義不大,但R2A相對較大,說明增加零件厚度會顯著增加其質量,而對機載產品來說,重量“寸土寸金”,因此俯仰支架厚度選擇6 mm即可。圓角大小及是否增加斜筋對最大應力指標影響較大,分別選取最佳水平B1、C2。故分析得到最佳水平組合為A1、B2、C3,即支架厚度6 mm,斷裂處圓角大小R為10 mm,兩側設計斜筋加固。
2.1.4 俯仰支架優化結果
優化后仿真結果如圖6所示,應力云圖中已無應力集中位置,最大應力27.4 MPa。根據3ε原則,該俯仰支架所受應力為82.2 MPa,遠小于LY12鋁合金屈服強度325 MPa,可認為其不會斷裂,滿足設計要求。

圖6 優化設計后俯仰支架應力云圖
本實驗僅以實際使用中斷裂的俯仰左支架為例,利用正交實驗法對其進行優化設計,該方法計算簡單,僅須做各因素部分水平的組合即可分析出各因素對指標的影響,具有很好的推廣性,天線其他結構件亦可使用該方法進行優化設計。
2.2 提高模塊安裝組件的固有頻率
天線模塊安裝板上有功率放大器、變頻器、三合一電源、伺服控制模塊等,通過螺接方式固定于主軸橫梁上。根據振動實驗及實際使用情況,電源、變頻器等模塊常出現開焊、板件損壞等問題,本文擬通過提高模塊安裝組件固有頻率來增強其抗振動的能力。將模塊安裝組件簡化為一簡單懸臂梁,如圖7所示。
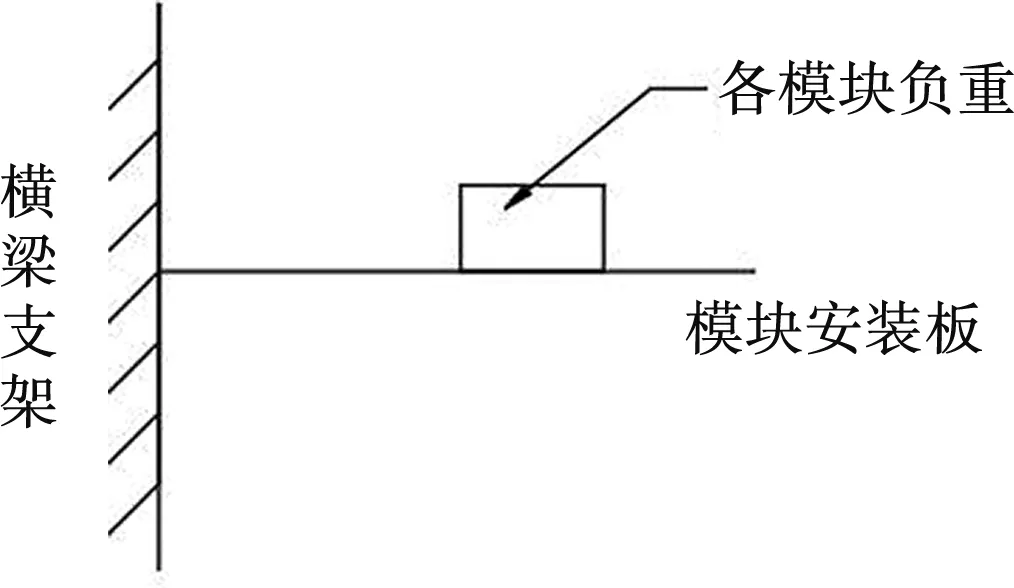
圖7 模塊安裝組件簡化圖
針對歐拉-伯努利梁,其自由運動微分方程為
(3)
利用分離變量法,令
w(x,t)=W(x)T(t)
(4)
則式(3)化簡為
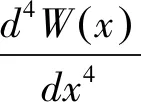
(5)
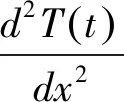
(6)
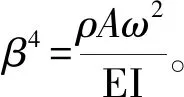
梁的固有頻率ω的解為
(7)
式中,β取值與梁的邊界條件有關。
懸臂梁其邊界條件如下:
X=0時,
X=L時,
由材料力學可知梁末端靜撓度為
(8)
則彈性系數為
(9)
式中,P為等效重力;l為重心距離固定端距離;EI為模塊安裝組件彎曲剛度。
可推出模塊安裝組件振動微分方程:
(10)
即
(11)
則系統頻率為
(12)
對天線進行模態計算,計算結果如表5所示。
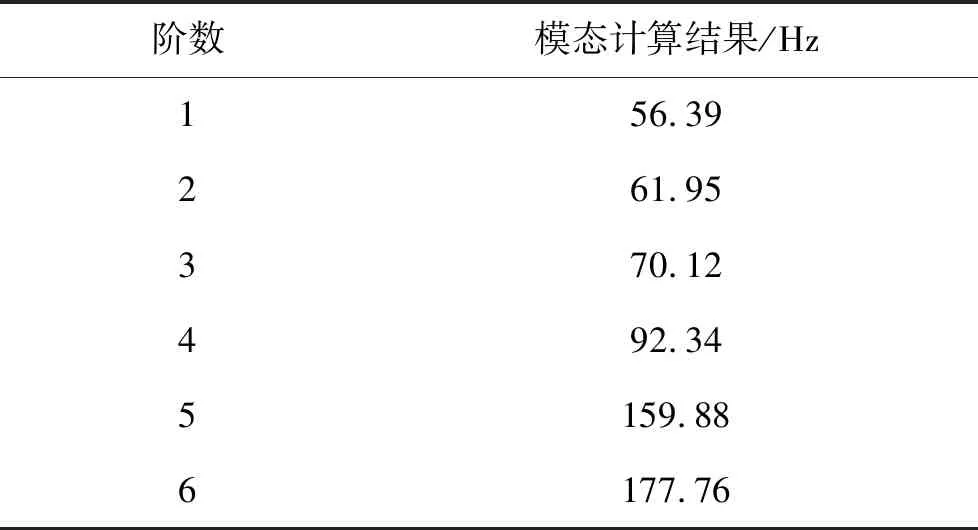
表5 天線模態分析結果
可見該款天線一階、二階模態較低,根據裝機飛行經驗以及相應振動實驗,一般只須關注前幾階模態數值,因為低階固有頻率對設備影響較大,結構件所受應力較大、變形明顯,因此提高設備一、二階固有頻率就可顯著提高設備的耐振動性能。
由上述計算可知,減輕系統重量m、縮小重心至固定端距離l,均可有效提高系統的固有頻率,因此嘗試去掉電源模塊與伺服控制器之間的轉接件,直接在三合一電源蓋板上攻螺紋孔,將伺服控制器直接安裝于電源模塊蓋板上方。為縮小重心至模塊固定端的距離,伺服控制器的擺放位置可盡量向內側推進。
對改進后的結構進行仿真分析,模態計算結果如表6所示。可以看出該款天線一階頻率大于60,根據裝機經驗可認為該款天線剛性較好,抗振動性能有較大改善。理論一階振型位移應變云圖如圖8所示。
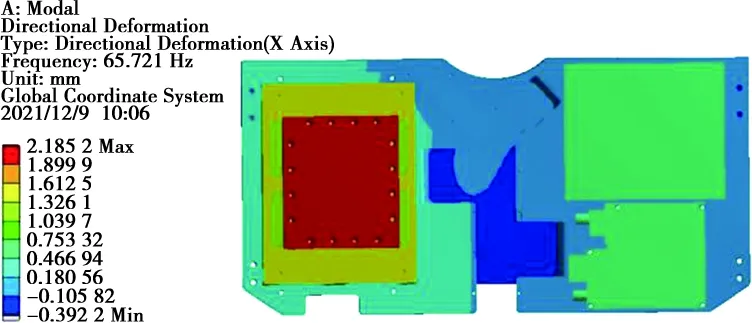
圖8 理論一階模態位移應變云圖
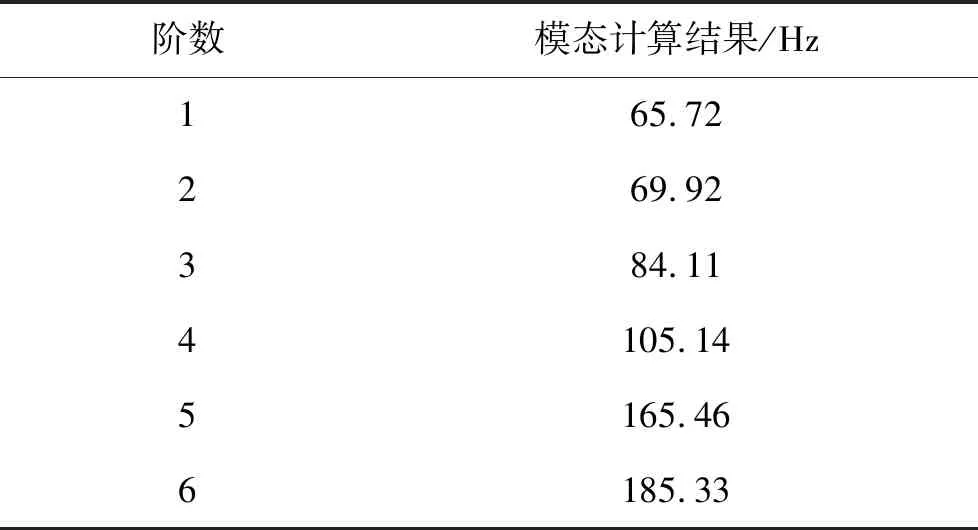
表6 改進后天線模態分析結果
2.3 增強天線抗振動性能的其他方式
除上述方法外,其他一些方法也可增強該款天線的抗振動能力,如減輕質量、增加阻尼等。
由頻響函數可知,其他條件不變,減輕系統重量可有效提高系統固有頻率。在保證結構強度的前提下各大型零件進行合理的輕量化設計,圖9為橫梁支架的背部輕量化設計示意圖,其背部的減重設計不但大幅減輕了結構件重量,而且余料以加強筋的形式保證了結構件強度[5-7]。

圖9 橫梁支架背部輕量化設計示意圖
由頻響函數可知,增加阻尼不能改變設備的固有頻率,但是可以降低共振放大。可在脆弱模塊部分增加被動隔振,比如在安裝功放模塊時,在模塊安裝板與功放之間位置加裝鋼絲繩隔振器,從而將振動能量轉化為隔振器的位移,以保護功放等脆弱模塊。
3 結束語
本文通過正交實驗優化了部分零件結構,減少了天線結構件應力集中,并通過減少轉接件的方式提高了天線固有頻率,從而增強了天線的抗振動性能。系列方法具有良好的推廣性,為機載產品的結構優化設計以及實際生產提供了參考。

