顧及多因子影響的中國區域Tm模型精化研究

李浩杰 劉立龍 黃良珂 莫智翔 蔡 猛

1 桂林理工大學測繪地理信息學院，桂林市雁山街319號，541006 2 廣西空間信息與測繪重點實驗室，桂林市雁山街319號，541006

在基于地基GNSS反演PWV過程中，水汽轉換系數K是反演大氣可降水量(precipitable water vapor，PWV)的關鍵參數之一，而K值精度取決于大氣加權平均溫度Tm的質量。Tm為地表到對流層高度大氣中溫度與水汽壓連續積分的結果，溫度和水汽壓信息可通過探空站或大氣再分析資料獲得，但其無法滿足用戶實時獲取任意位置溫度和水汽壓信息的需求。因此，通常需要建立合適的Tm經驗模型。根據模型建立所采用的回歸分析方法可將現有的Tm模型分為兩類：第一類為基于線性條件的局部或全球Tm模型；第二類為基于非線性條件的局部或全球Tm模型，該模型在無氣象參數的條件下能夠基于局部或全球多年Tm數據擬合獲得，雖然使用方便，但其精度與包含氣象參數的模型相比略有不足。眾多學者已建立多種中國區域Tm模型[1-9]，并取得豐富的研究成果。但隨著研究的深入發現，Tm模型受地表溫度、地表水汽壓、高程和緯度等多因素的綜合影響。因此，本文利用中國區域2015～2017年84個探空站的數據，在Bevis模型基礎上，建立一種顧及以上因素影響的中國區域Tm模型BET，并以2018年探空站Tm數據為參考值，檢驗BET模型的精度。

1 數據來源及Tm計算

1.1 數據來源

本文從美國懷俄明州立大學網站(http:∥weather.uwyo.edu/upperair/sounding.html)獲得中國區域2015～2018年84個探空站的數據，包含每隔12 h的氣壓、溫度、露點溫度、相對濕度等相關氣象數據，同時可提供地表測站經度、緯度及高程信息。中國區域探空站具體分布如圖1所示。

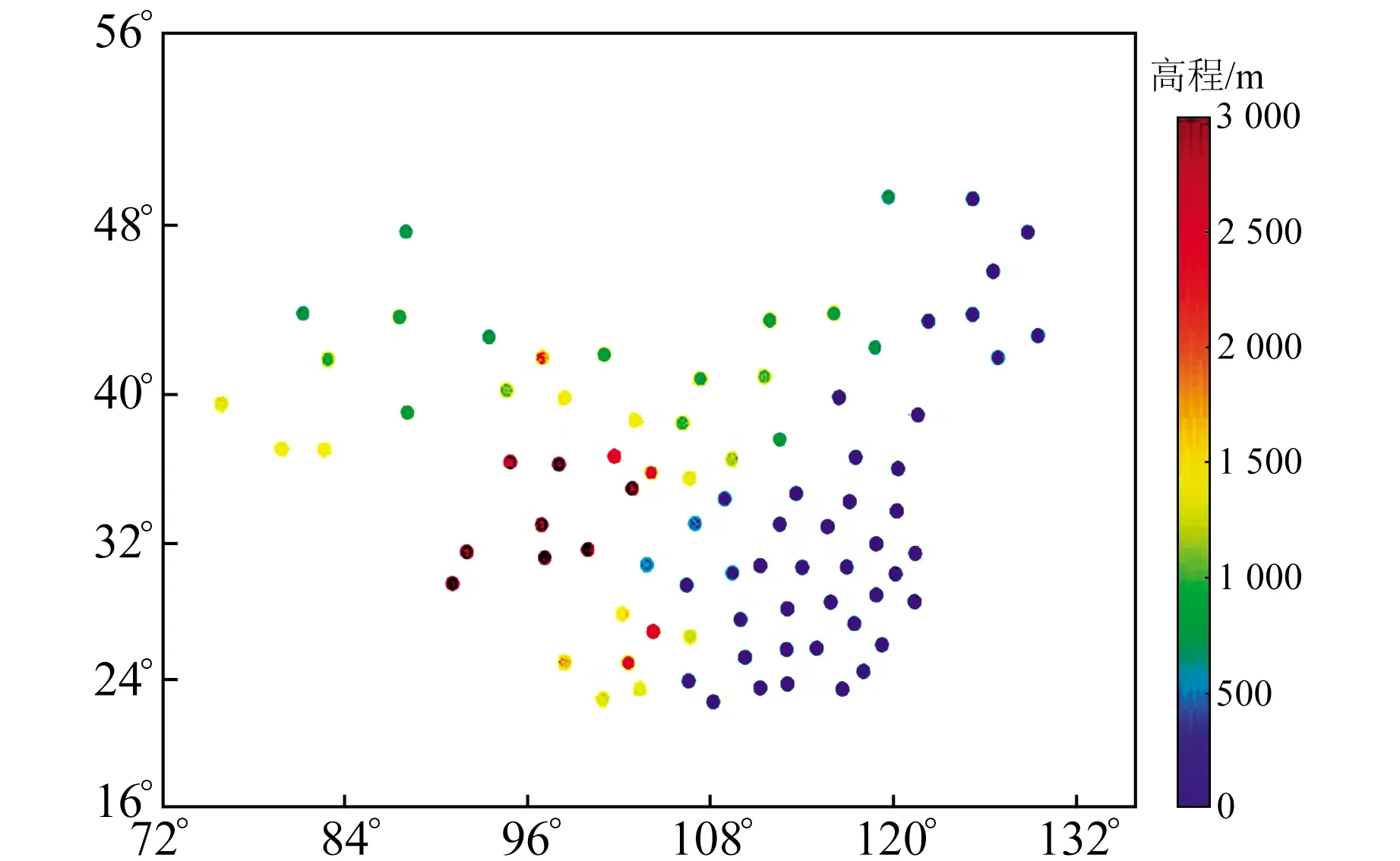
圖1 中國地區84個探空站分布

1.2 Tm計算原理與常用模型

Tm為水汽壓e和絕對溫度T沿天頂方向的積分值，其計算過程詳見文獻[4]。

對于缺乏探空資料的地區，Tm難以精確求得。因此，Bevis等[10]建立廣泛應用于中緯度地區的單因子回歸模型Tm-Ts：

Tm=70.2+0.72×Ts

(1)

2 中國地區Tm模型建立

2.1 Tm模型影響因素相關性分析

為研究中國區域Tm與Ts、es、高程和緯度的關系，利用中國地區2015～2017年84個探空站的數據，選用皮爾遜(Pearson)相關系數R進行Tm與Ts、es、高程和緯度的相關性分析：

(2)

式中，n為樣本數量，X和Y表示2個不同變量。R大于0.5為高度相關，在0.3～0.5之間為中度相關，在0.1～0.3之間為弱相關[11]。

經計算可得，中國地區Tm與Ts、es的相關系數分別為0.92和0.91，說明Tm與Ts、es之間存在強相關性；Tm與高程和緯度的相關系數分別為0.38和0.45，呈現中度相關性。從相關性程度來看，在建立中國地區Tm模型時，需要考慮Ts、es、緯度和高程對Tm模型精度的影響。

2.2 Tm模型建立

本文參考文獻[1-3]的建模方式，在Bevis模型基礎上，基于中國區域Ts、es、緯度和高程因子，建立一種新的Tm模型BET：

A5×H+A6×L

(3)

式中，H為測站高程，L為測站緯度，A1、A2、A3、A4、A5和A6均為模型系數。

采用2015～2017年中國區域84個探空站點觀測的Ts、es、H、L數據來確定BET模型系數，具體方法為：利用數值積分方法計算中國區域各個探空站Tm值，再將探空站對應的Tm、Ts、es、H和L數據代入式(3)進行最小二乘擬合計算。表1為獲得的BET模型參數。

表1 BET模型系數

3 Tm模型精度檢驗

為檢驗本文建立的BET模型精度，以2018年中國地區84個探空站Tm數據為參考值，分別對Bevis、BET、GPT3w-1、GPT3w-5模型的均方根誤差(RMSE)和平均偏差(bias)進行分析：

(4)

(5)

式中，N為預測樣本數量，Xt、Pt分別為Tm真實值與不同模型預測值。

3.1 Tm模型在中國區域的精度檢驗

為檢驗BET模型的精度，以中國區域2018年探空站Tm數據為參考值，分別與目前廣泛使用的Bevis模型和GPT3模型進行對比，其中GPT3模型提供1°×1°和5°×5°分辨率的Tm計算模型(分別簡稱GPT3w-1、GPT3w-5)。表2為4種模型在中國區域各個探空站的RMSE和bias統計。

表2 2018年各模型RMSE與bias統計

由表2可知，Bevis模型在中國區域bias最大值的絕對值大于最小值的絕對值，而GPT3模型相反，BET模型bias最大值與最小值的絕對值基本相同。從bias年均值可以看出，Bevis模型在中國區域存在明顯的正bias，GPT3模型在中國區域表現為明顯的負bias，而BET模型表現為較小bias。同時，在中國區域GPT3w-5模型表現出較大的RMSE，年均RMSE達到5.17 K；GPT3w-1模型與Bevis模型RMSE相差較小，年均RMSE分別為4.45 K和4.69 K，說明GPT3w-1模型精度優于GPT3w-5模型。BET模型精度最優，其年均RMSE與Bevis模型相比降低29.2%，與GPT3w-1和GPT3w-5模型相比分別降低32.8%和39.1%，說明BET模型在中國區域相比于以上3種模型具有較好的精度。

為分析BET模型在中國不同區域的精度，以2018年探空站Tm數據為參考值，分別計算4種模型在各個探空站的年均RMSE和bias，結果見圖2和圖3。

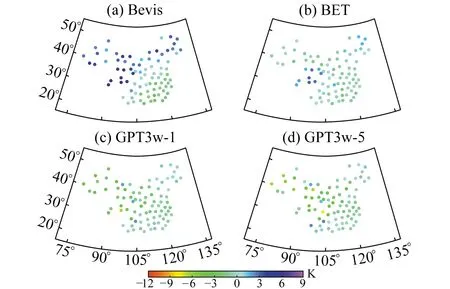
圖2 4種模型2018年各探空站年均bias分布

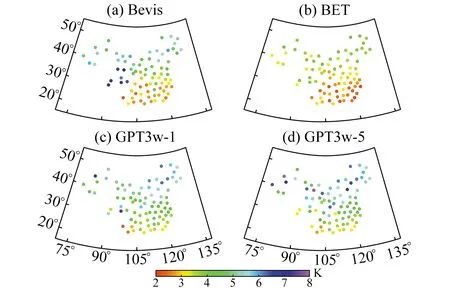
圖3 4種模型2018年各探空站年均RMSE分布

從圖2可以看出，Bevis模型在新疆、西藏、四川、青海、內蒙古、黑龍江、吉林和遼寧地區存在較大的正bias；在中國南部區域bias分布在-3～0 K之間；在中國中部、云南和廣西等地區bias在0 K左右。說明Bevis模型在中國地區適應性略差，其主要原因為中國地區高程起伏較大并跨越較大緯度。GPT3w-1與GPT3w-5模型整體上呈現負bias，在中國東部地區bias為0 K左右，在中國西部地區bias低于-3 K。其原因為中國西部地區高程起伏較大，而GPT3模型未顧及高程對Tm模型精度的影響。BET模型在中國區域bias整體分布在0 K左右，部分區域bias的絕對值小于3 K，相比于其他3種模型其bias較小且穩定。

由圖3可知，Bevis模型在中國南部區域RMSE在3 K左右，在中國北部區域RMSE在3～6 K之間，在四川和青海地區RMSE可達到7 K左右。GPT3模型在中國區域由南向北RMSE由3 K逐漸增加到6 K左右，在新疆部分區域可達到8 K左右，其中GPT3w-1模型在中國南部地區RMSE優于GPT3w-5模型。BET模型在中國南部和中部地區RMSE在3 K以內，在中國東北三省、內蒙古和新疆區域RMSE在4 K以內，相比于Bevis模型與GPT3模型，BET模型在中國區域的整體適應性與穩定性更好。

3.2 測站高程和緯度對模型精度的顯著性分析

結合以上分析及已有研究表明[9]，測站高程和緯度對Tm模型精度的影響較大。為進一步說明高程與緯度對BET模型精度的影響，使用文獻[1-3]中方法，建立基于地表溫度和地表水汽壓的中國區域Tm模型(簡稱BE模型)，繪制BE和BET模型在高程(圖4)和緯度(圖5)變化情況下中國區域各探空站2018年RMSE和bias年均值。

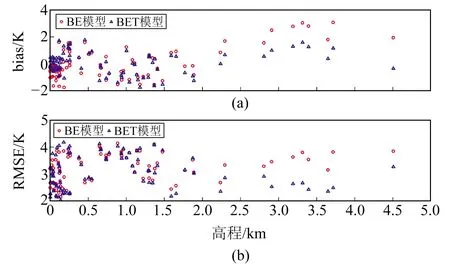
圖4 BE和BET模型在高程變化情況下年均bias和RMSE

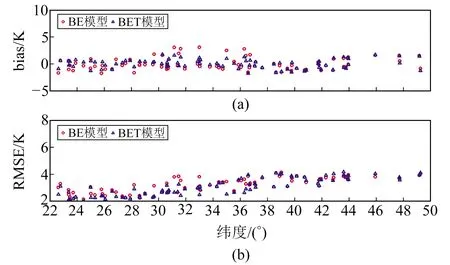
圖5 BE和BET模型在緯度變化情況下年均bias和RMSE

由圖4可知，相比于BE模型，考慮高程和緯度的BET模型在測站高程大于2.5 km時RMSE和bias得到較大改善，在高度低于2.5 km時2種模型的RMSE和bias相當，說明引入高程因子的BET模型在中國區域的整體適應性優于BE模型。由圖5可知，BET模型在緯度22°～40°之間的RMSE與bias均優于BE模型，在高緯度地區，BE模型的RMSE和bias與BET模型相當。

綜上可知，在中國區域考慮高程和緯度因子的BET模型能在一定程度上提高Tm的計算精度。

3.3 BET模型與Bevis模型和GPT3模型對比分析

為分析4種模型在不同高程和緯度下的穩定性與適應性，繪制各模型在高程(圖6)和緯度(圖7)變化情況下各探空站2018年RMSE與bias年均值。

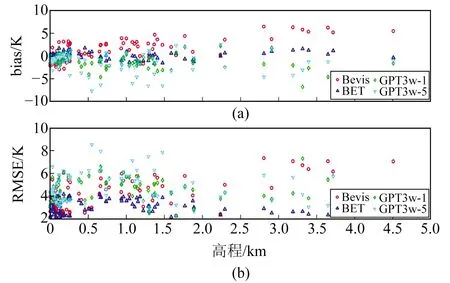
圖6 4種模型在高程變化情況下年均bias和RMSE

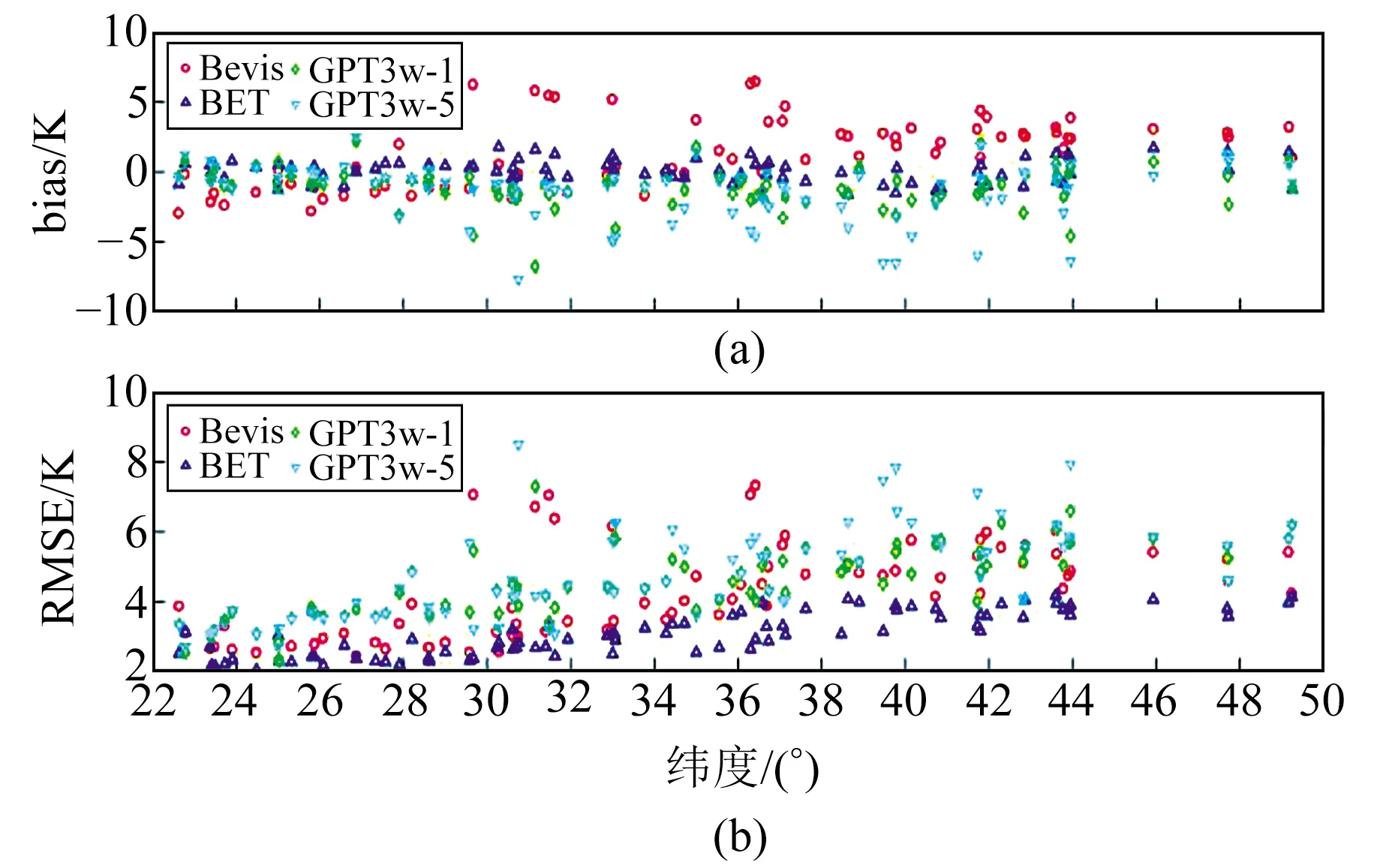
圖7 4種模型在緯度變化情況下年均bias和RMSE

由圖6可知，BET模型的bias和RMSE分別在0 K左右和2～4 K之間波動，而Bevis模型和GPT3模型的bias和RMSE分別在-10～10 K和2～10 K之間波動。其原因為Bevis模型和GPT3模型未考慮高程對Tm模型精度的影響，說明BET模型在中國區域抗高程干擾能力優于GPT3模型和Bevis模型，進一步說明BET模型在中國區域的穩定性與適應性優于GPT3模型與Bevis模型。

由圖7(a)可知，在中國區域當緯度低于30°時，4種模型的bias均集中分布在0 K左右；當緯度高于30°時，Bevis模型和GPT3模型的bias分別在0～10 K和-10～2 K之間波動，GPT3w-5模型的波動趨勢大于GPT3w-1模型，BET模型的bias集中分布在0 K左右；當緯度高于40°時，BET模型的bias整體大于0 K。Sun等[12]研究發現，中國中高緯度地區Tm變化更加劇烈，經驗模型在該地區的精度相對于其他地區會有所損失，這可能是導致BET模型在該地區bias大于0 K的原因。但即使如此，BET模型在高緯度地區的RMSE也在4 K以內，優于Bevis模型和GPT3模型。綜合來看，BET模型在中國區域的bias抵抗緯度變化的能力優于Bevis模型和GPT3模型。由圖7(b)可知，4種模型的RMSE均有隨緯度上升而增加的趨勢，但BET模型的RMSE集中在2～4 K之間，其隨緯度上升而增加的趨勢明顯低于Bevis模型與GPT3模型。說明在中國區域，BET模型的RMSE對緯度變化的適應性與穩定性優于Bevis模型和GPT3模型。

總體而言，在中國不同區域、不同高程和不同緯度情況下，BET模型的RMSE和bias均小于Bevis模型與GPT3模型，其在中國區域的穩定性與適應性也均優于Bevis模型與GPT3模型。

4 結 語

1)本文采用2015～2018年84個探空站的數據，對影響中國區域Tm模型精度的各個因素進行綜合分析，建立適用于中國區域的基于地表溫度、地表水汽壓、高程和緯度的Tm精化模型，并取得較好的精度，其年均RMSE和bias分別為3.15 K和0.04 K。

2)將建立的BET模型與廣泛應用的Bevis模型和GPT3模型進行對比，BET模型相比于Bevis、GPT3w-1、GPT3w-5模型，年均RMSE和bias分別降低29.2%和96.4%、32.8%和96.7%、39.1%和97.4%。表明在中國區域，BET模型的精度優于Bevis模型和GPT3模型。

3)BET模型在中國不同區域的RMSE與bias均優于Bevis模型和GPT3模型，且BET模型的RSME和bias抵抗高程和緯度變化的能力優于Bevis模型和GPT3模型。說明在中國區域，BET模型的穩定性與適應性優于Bevis模型和GPT3模型。