基于有限時間引導律的欠驅智能船舶循跡控制

馮輝，胡勝，余文曌，*，徐海祥

（1.高性能船舶技術教育部重點實驗室，武漢 430063； 2.武漢理工大學 船海與能源動力工程學院，武漢 430063）

在大數據和人工智能等新興技術的影響下，研究無人化、綠色和安全的智能船舶已是大勢所趨。作為智能船舶關鍵功能之一，智能航行受到了廣泛的關注并得到了迅速的發展［1］。其中，循跡控制是實現智能航行功能的關鍵技術之一。

循跡控制是指控制欠驅智能船舶沿著一條預定的路徑航行，并且這條路徑與時間無關［2］。目前，國內外關于循跡控制的研究已有較多成果。Encarna??o等［3］在Serret-Frenet坐標系中依據期望路徑重新定義輸出信號，將控制目標轉化為位置誤差和艏向角誤差，但缺點是控制器的設計十分復雜。為了簡化控制器的設計，有學者將循跡控制系統分為2個子系統：引導律和控制系統［2］。在獲得路徑信息和環境信息后，引導律計算出控制系統的輸入信號，即期望艏向角；控制系統則產生相應的控制信號，使船舶的實際艏向跟蹤引導律給出的信號，完成循跡控制目標。

LOS（line-of-sight）引導律［4］因其結構簡單、收斂性好等優點而被廣泛應用于循跡控制。但在實際運行環境中，船舶受到風浪流等環境因素的干擾，即橫向環境力的作用，在循跡過程中會存在漂角。但欠驅動結構無法產生橫向的控制力，因此船舶的實際運動軌跡將偏離期望的運動軌跡，限制了傳統LOS引導律的應用。因此，如何減小漂角對循跡效果的影響是目前的研究熱點。

減小漂角影響的一種最直接的方法就是測量漂角。文獻［5］使用加速度計測量橫向和縱向的加速度，再通過積分得到橫向和縱向速度，進而計算出漂角，但缺點是加速度的測量值易受噪聲的污染從而導致計算出的速度存在較大的誤差。文獻［6］利用全球導航系統計算漂角，但成本較高且精確性較差。另一種方法是利用積分LOS（ILOS）引導律。B?rhaug等［7］針對傳統LOS引導律無法抵抗環境干擾的問題，提出了一種應用廣泛、具有積分作用的ILOS引導律，并證明了其全局一致漸進穩定性。文獻［8-9］在B?rhaug等［7］的基礎上，在設計引導律時考慮了航速，簡化了參數調整過程，但使得該算法的響應速度易受航速的影響。文獻［10］針對直線接圓弧路徑不連續問題提出了一種參數化ILOS引導律，使控制輸出更加平滑，但引導效果易受期望路徑插值的邊界條件影響。文獻［11］設計時變增益的ILOS引導律減小位置超調，但前向距離的上限和下限難以確定。文獻［12］提出一種自適應ILOS（ALOS）引導律，將漂角視為固定參數，通過設計自適應項估計漂角。文獻［13］在引導系統建模時考慮流速的影響，提出了一種直接ILOS引導律和間接ILOS引導律用以應對時變的海流，但無法應對其他未建模環境干擾的影響。文獻［14］設計了一種降階的擴張狀態觀測器，用來估計由外部干擾引起的時變漂角，但未考慮引導系統的有限時間穩定性。

近年來，有限時間控制方法因其更好的控制性能受到了廣泛的關注，并得到了迅速發展［15］。文獻［16］利用有限時間收斂的干擾觀測器，以估計時變的大漂角，提高了曲線循跡的精確性。文獻［17］提出了有限時間收斂的引導律，其不僅證明了漂角觀測器的有限時間收斂性，還證明了位置跟蹤誤差的有限時間收斂性，但該方法的缺點是漂角的估計值易受傳感器測量噪聲的影響。

本文在現有國內外研究的基礎上，提出了一種基于自適應控制理論的有限時間引導律，其控制參數可隨橫向偏差的變化而進行自適應調整，提升引導系統的響應速度，同時可適用于風浪流等環境載荷干擾下的欠驅智能船舶循跡控制，用于補償船舶在循跡過程中受到的流載荷的干擾，并證明了該引導律的有限時間穩定性。通過仿真實現了欠驅智能船舶水平面內的直線和曲線循跡，并進行了仿真對比實驗。

1 問題描述

1.1 船舶數學模型

欠驅船舶的水平面三自由度運動學和動力學方程如下［2］：

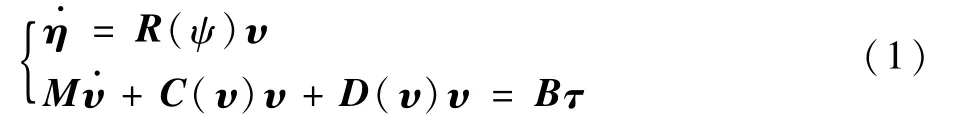
式中：η=［x，y，ψ］T為船舶在固定坐標系下的位置，x、y、ψ分別表示船舶在固定坐標系中的橫坐標、縱坐標、艏向角；R（ψ）為坐標系旋轉矩陣；υ=［u，v，r］T為船舶在運動坐標系下的運動速度，u、v、r分別表示船舶在運動坐標系中的縱向速度、橫向速度、轉艏角速度；M為包含水動力附加質量的慣性矩陣；C為包含附加質量的科里奧利向心力矩陣，由船舶自身和附加質量共同作用產生；D為阻尼系數矩陣；B為控制輸入配置矩陣；τ=［τu，0，τr］T為控制輸入矩陣，τu為船舶縱向推力，τr為轉艏力矩。

因此，可以通過在式（1）的運動學和動力學方程中加入海流的速度，建立流載荷干擾下的船舶操縱運動方程，如下：

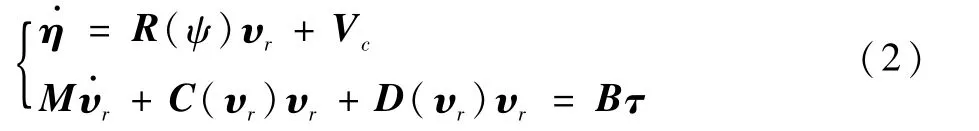
式中：υr=υ-Vc為船舶相對海流的速度。

1.2 有限時間穩定性

有限時間穩定是指系統狀態能在有限時間內收斂到平衡點。考慮如下系統：

式中：x（t）表示系統狀態；f：→Rn為包含原點的定義域 到n維空間Rn中的一個連續函數；0∈Rn表示零向量。

1.3 引導律

引導律的推導是在一個二維平面內完成的，其中，期望路徑通常由一系列路徑點（xp（θ），yp（θ））相連組成，如圖1所示，其中θ為大于零的路徑參數變量。圖中：γp為期望路徑上任意一點處的切線與正北方向的夾角，即Serret-Frenet坐標系與固定坐標系之間的旋轉角。

假設在固定坐標系中，船舶的位置坐標為（x，y）。由圖1可知，船舶在Serret-Frenet坐標系中的坐標為

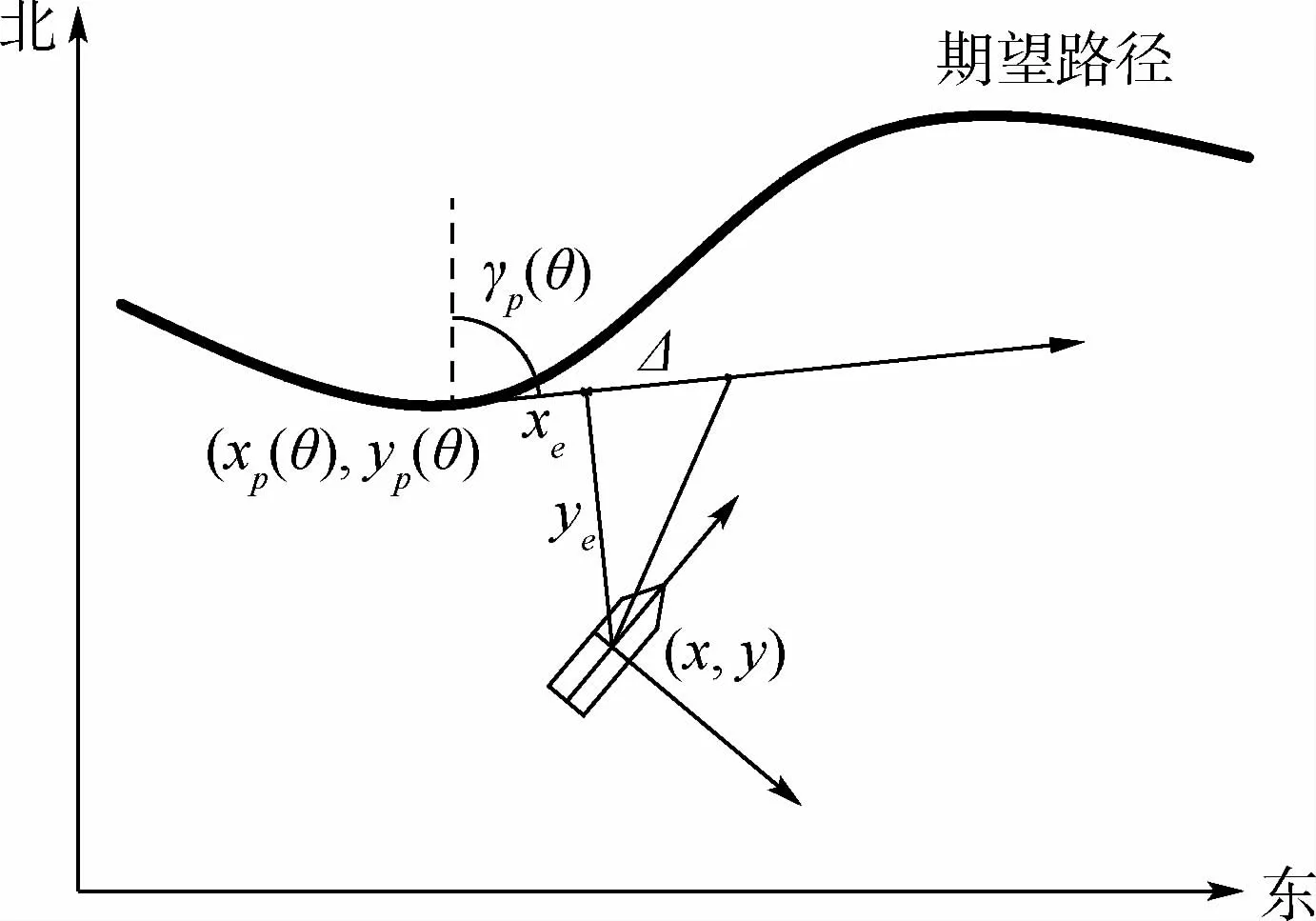
圖1 LOS引導律原理Fig.1 Geometrical illustration of LOS guidance law

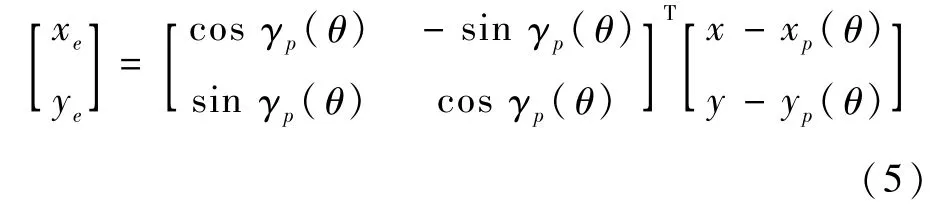
式中：xe為縱向偏差；ye為橫向偏差。

旋轉角γp定義如下：

式中：x′p（θ）=?xp/?θ；y′p（θ）=?yp/?θ。

假設1 通常在直線或者直線圓弧循跡時，xe并不影響引導律的引導效果，為了簡化計算，故假設xe=0。

假設3 船舶的實際艏向角可以準確跟蹤期望艏向角，即ψ=ψd。

由式（5）和假設1可得

由式（1）可知船舶的運動學方程為

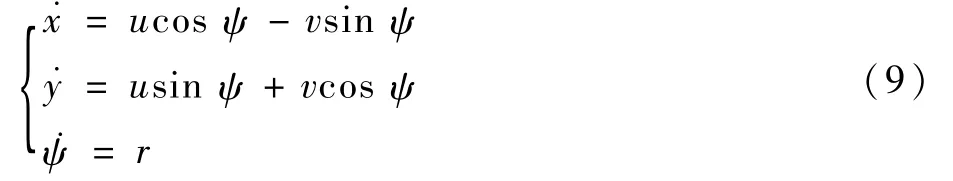
將式（9）代入式（8）得

注2 船舶在直線循跡或圓弧循跡時，漂角為一定值。但對于直線圓弧組成路徑，漂角會發生緩慢的變化。因為漂角的動態特性變化慢于控制帶寬變化，所以可通過自適應項估計漂角。

將式（10）展開，并結合假設2可得

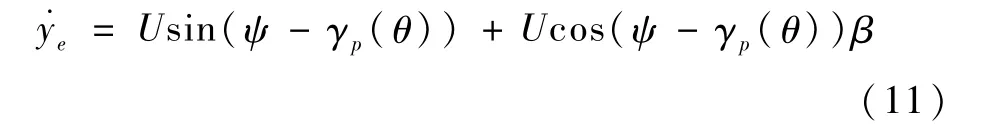
2 有限時間引導律

本文提出的有限時間引導律定義如下：

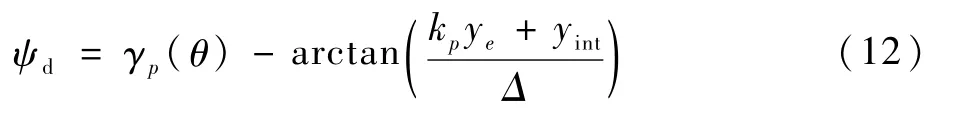
其中：參數k1＞0，k2＞0，參數0＜α＜1。

考慮到系統漂角β未知，建立如下誤差跟蹤系統：

定理1 對于系統（13），在滿足假設3的前提下，設計的引導律（12）可以使系統（13）有限時間穩定，即

式中：ε1和ε2為大于零的極小常數。

證明 將式（12）代入式（11）中可得

由于

將式（15）和式（16）代入式（14）得

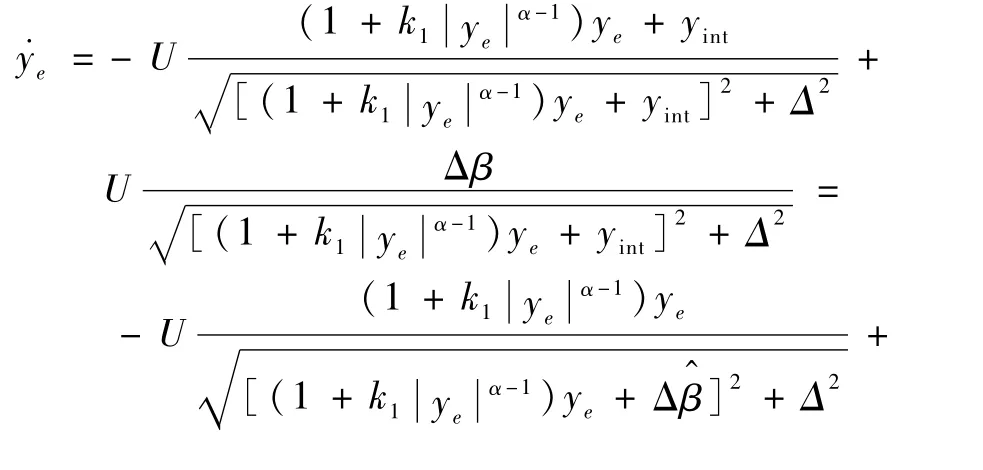
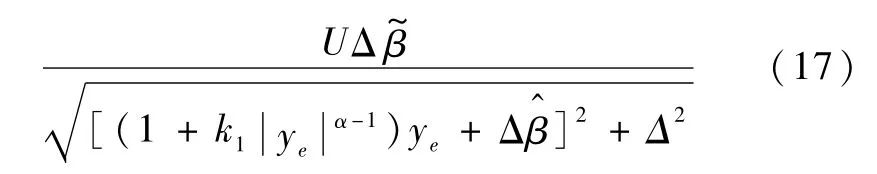
定義李雅普諾夫函數如下：

式（18）對時間求導并將式（17）代入可得

令

則式（19）可以改寫為

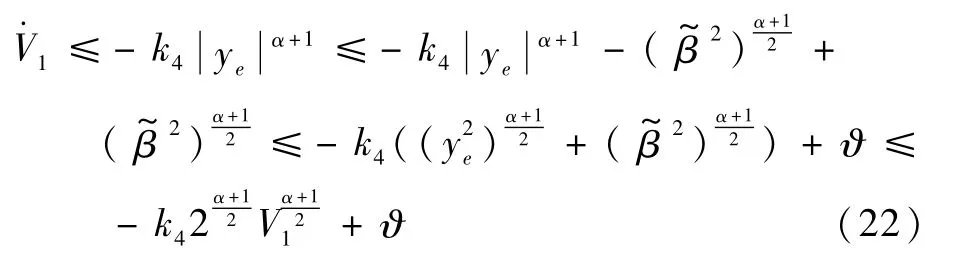
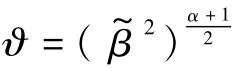
由文獻［18］可知，存在參數0＜θ0＜1，滿足：

得到

通過引理1可知，系統（13）是有限時間穩定的，并且收斂時間T1滿足：

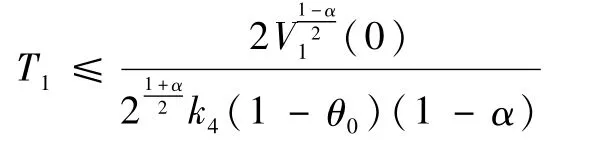
證畢

3 仿真實驗

3.1 仿真條件

為了驗證本文所提出的有限時間引導律的有效性，以武漢理工大學一艘欠驅智能船舶為模型進行了直線循跡仿真實驗和曲線循跡仿真實驗，并與文獻［7］中的ILOS引導律進行對比分析，采用PID控制算法進行縱向和艏向控制器設計。

3.2 仿真結果與分析

1）直線循跡仿真

仿真條件設置如表1所示，引導律參數k1=1，α=0.8，k2=0.008。其他仿真條件如表1所示。

直線循跡的期望路徑為連接表1中2個路徑點的直線。圖2為直線循跡航行路徑曲線，圖3為直線循跡橫向偏差曲線。圖2表示2種方法均能引導船舶沿期望路徑航行。但是從圖3中可以看出，本文引導律可以使ye更快地收斂至零且沒有超調，大約在t=110 s時收斂至零；傳統ILOS引導律的ye收斂速度較慢，大約在t=150 s時收斂至零。由此可知，本文引導律相比傳統ILOS引導律在直線循跡時，ye的收斂速度更快，具有更好的引導效果。圖4為比例系數kp隨時間變化曲線。圖5表示2種方法的實際艏向角都可以較好地跟蹤期望值。

圖3 直線循跡橫向偏差曲線Fig.3 Curves of straight-line path following cross-track error

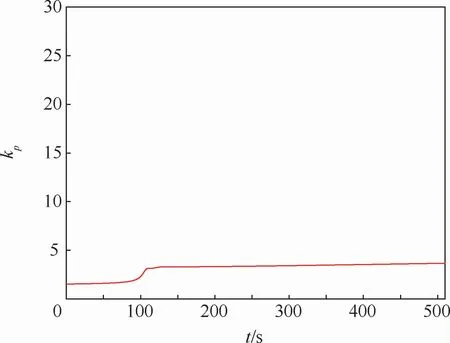
圖4 直線循跡引導律比例系數變化曲線Fig.4 Curve of straight-line path following guidance law proportional coefficient

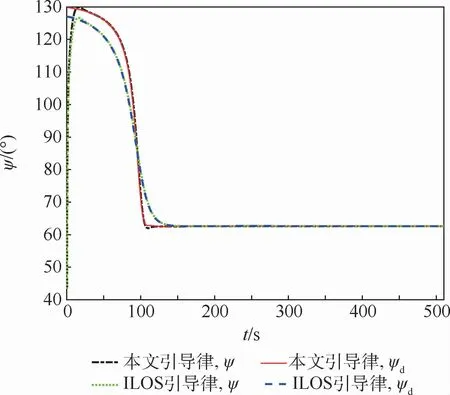
圖5 直線循跡艏向角變化曲線Fig.5 Curves of straight-line path following heading angle

表1 直線循跡仿真條件Table 1 Simulation conditions of str aight-line path following

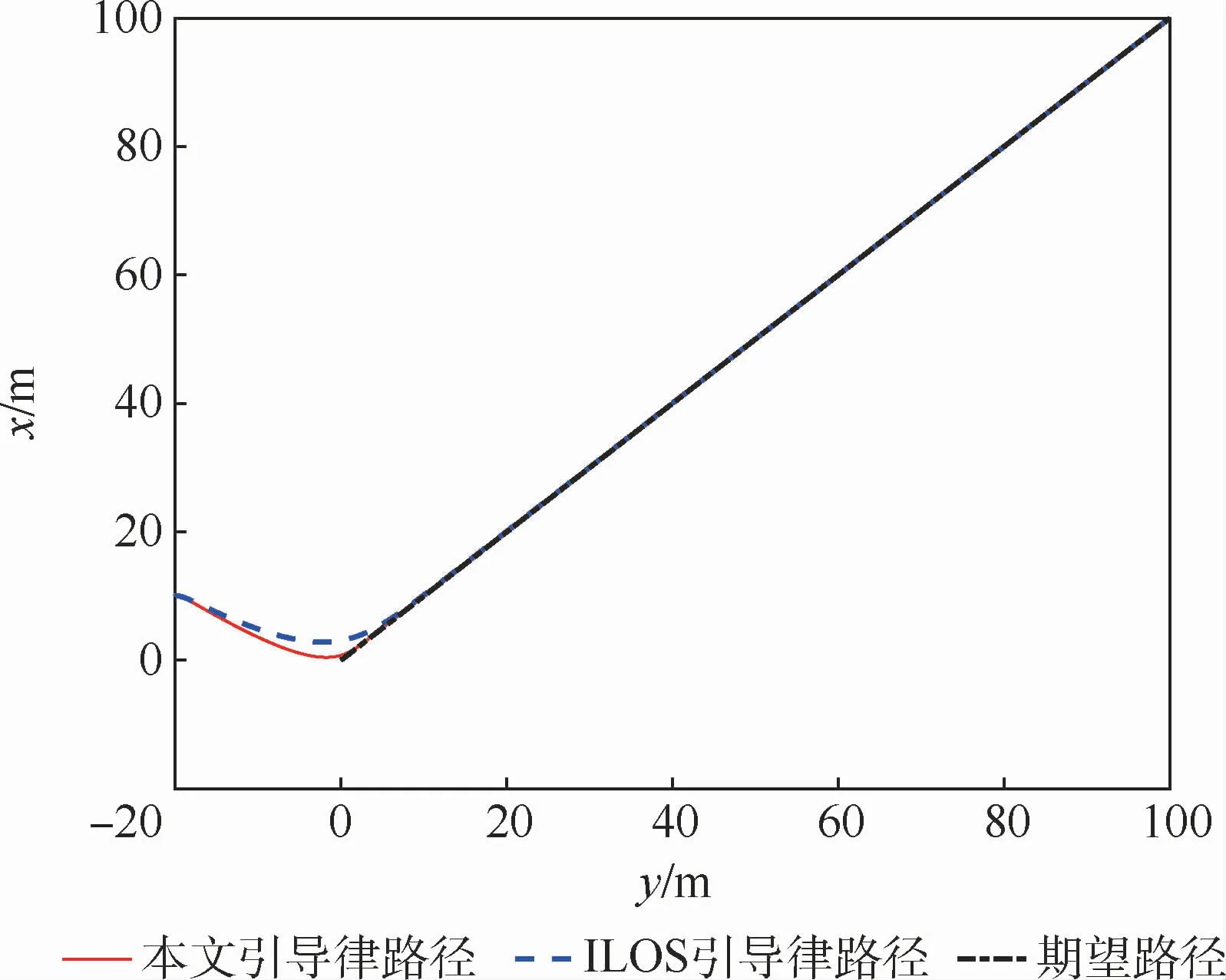
圖2 直線循跡曲線Fig.2 Curves of straight-line path following

2）曲線循跡仿真

仿真條件設置如表2所示，引導律參數k1=0.4，α=0.8，k2=1。其他仿真條件如表2所示。曲線循跡的期望路徑為連接表2中5個路徑點的直線圓弧曲線。圖6為曲線循跡航行路徑曲線，圖7為曲線循跡橫向偏差曲線。圖6表示2種方法均能引導船舶沿期望的曲線路徑航行，但本文引導律的路徑更接近期望路徑。為了進一步比較2種方法引導效果的優劣，從圖7中可以看出，本文引導律的ye收斂速度更快。在3處轉彎路徑處，ye由于曲率的增大而增大，本文引導律的ye的峰值分別為0.01 m、0.04 m和0.04 m，傳統ILOS引導律的ye的峰值分別為0.03 m、0.3 m和0.3 m；本文引導律的ye重新收斂至零所花費的時間分別為148 s、127 s和127 s，傳統ILOS引導律的ye又重新收斂至零所花費的時間分別為148 s、241 s和241 s。圖8為比例系數kp隨時間變化曲線。

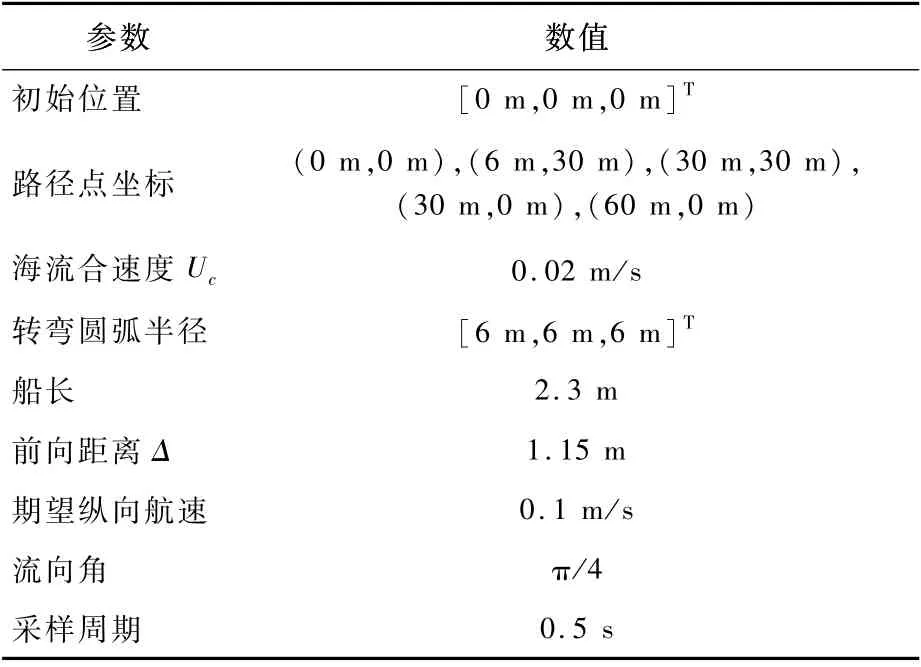
表2 曲線循跡仿真條件Table 2 Simulation conditions of curved-line path following

圖6 曲線循跡曲線Fig.6 Curves of curved-line path following

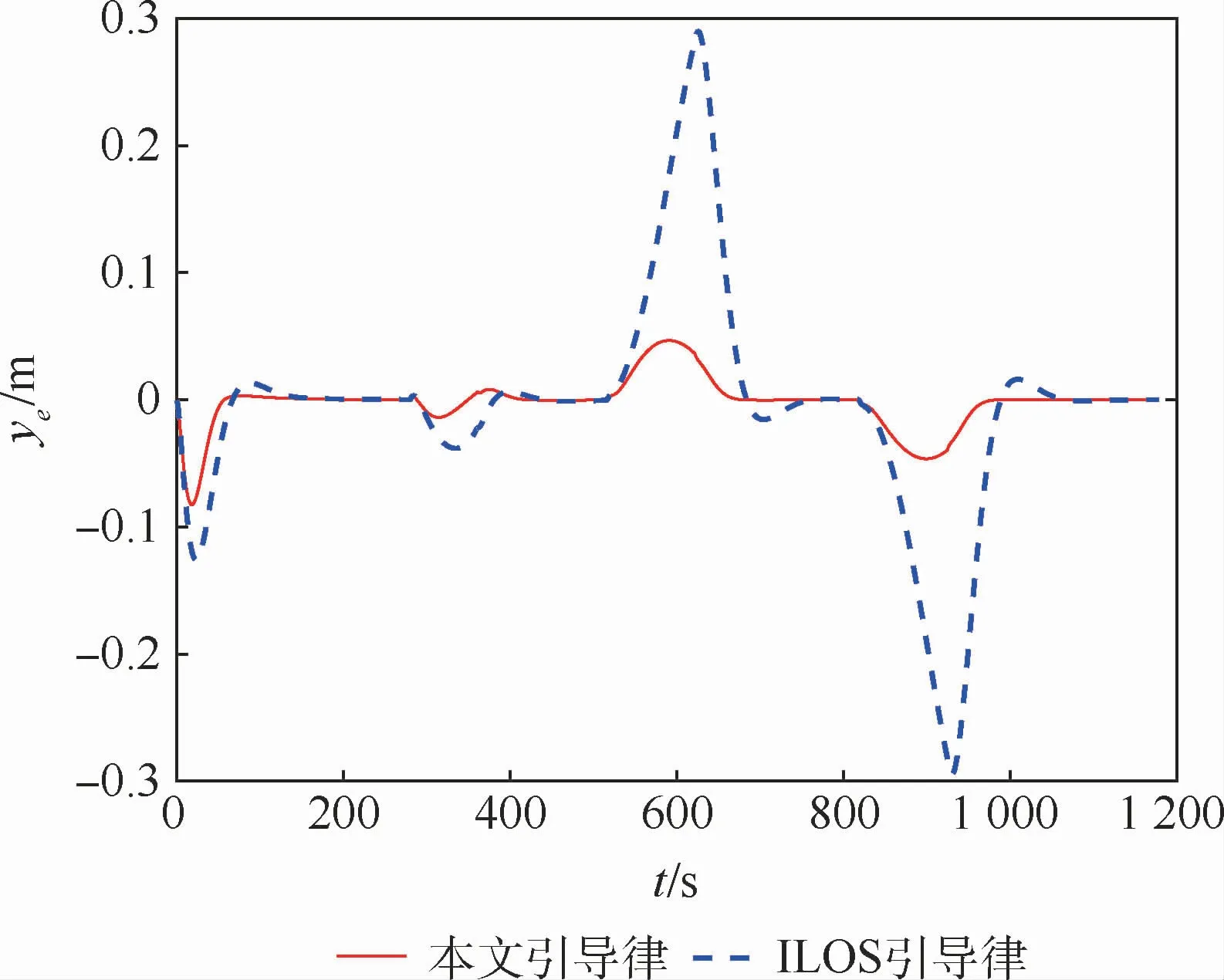
圖7 曲線循跡橫向偏差曲線Fig.7 Curves of curved-line path following cross-track error

結合圖3和圖4、圖7和圖8分析可知，比例系數隨橫向偏差的變化關系有大誤差、小增益和小誤差、大增益的特點。由圖7和圖8可知，當橫向偏差穩定于零附近時，比例系數有較大的變化（如圖中的80～280 s，448～515 s，697～816 s，997～1 175 s），原因是：橫向偏差此時是一個逐漸趨近零的極小值，而比例系數對趨近零的極小值變化非常敏感，因此比例系數在此過程中變化較大。但由于橫向偏差是極小值，當橫向偏差趨于零時，比例系數的變化并不會影響引導效果。

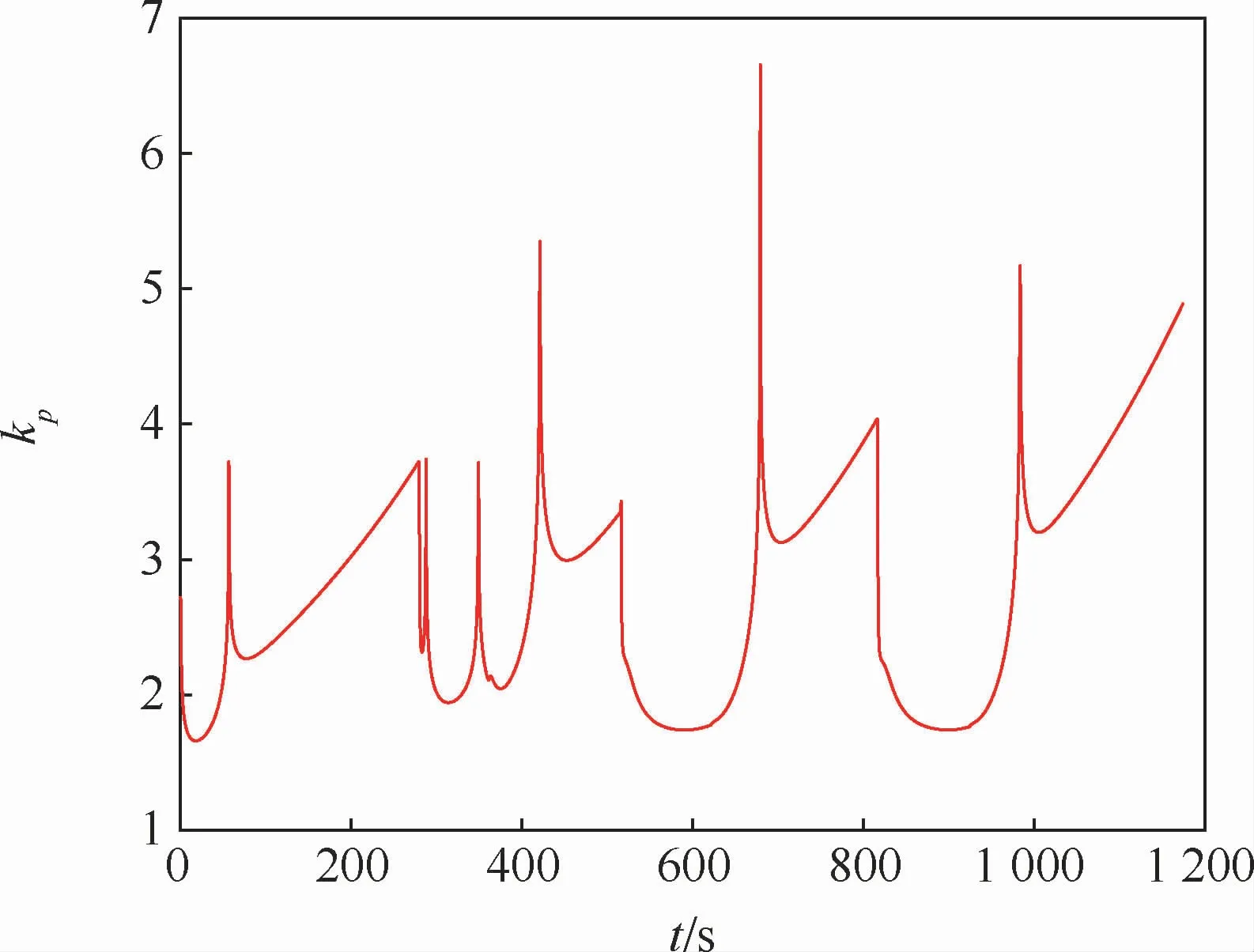
圖8 曲線循跡引導律比例系數變化曲線Fig.8 Curve of curved-line path following guidance law proportional coefficient

圖9表示曲線循跡情況下，2種方法的實際艏向角也都可以較好地跟蹤期望值。從圖5和圖9的艏向角對比曲線可以看出，在相同PID控制參數控制下，2種方法的艏向角跟蹤效果都較好，但2種方法計算的期望艏向角不同，證明本文引導律計算的期望艏向角相比傳統ILOS引導律更加合理和有效。

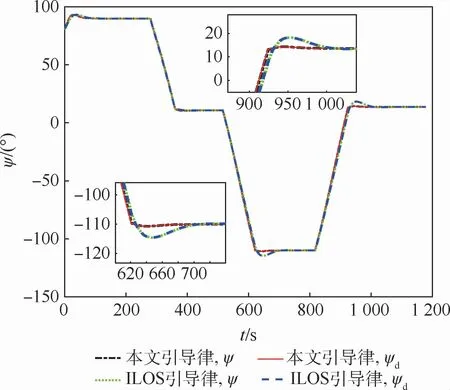
圖9 曲線循跡艏向角變化曲線Fig.9 Curves of curved-line path following heading angle

4 結 論

經過理論分析和仿真對比實驗，得到以下結論：

1）所提出的有限時間引導律適用于直線循跡和曲線循跡，設計的自適應項可以補償環境干擾和路徑曲率對循跡效果的影響。

2）基于有限時間穩定理論證明了漂角未知時，橫向偏差控制系統在應用所提出的有限時間引導律時是有限時間穩定的。

3）通過直線循跡和曲線循跡仿真對比實驗結果可知，相比于傳統ILOS引導律，本文所提出的有限時間引導律可以使橫向偏差更快收斂至零附近且超調量更小。

綜上所述，對于欠驅智能船舶循跡控制，提出的有限時間引導律具有更大的應用潛力。本文未涉及控制器研究，但船舶運動受模型不確定和時變外部環境干擾的影響，將導致動力學控制性能變差，因此，下一步將研究模型不確定和時變外部環境干擾情況下欠驅智能船舶循跡控制器設計問題。