變質(zhì)心固定翼無人機(jī)動(dòng)力學(xué)分析與抗擾控制

邱瀟頎，高長(zhǎng)生，荊武興

（哈爾濱工業(yè)大學(xué) 航天學(xué)院，哈爾濱 150001）

變質(zhì)心控制通過安裝在飛行器內(nèi)部的質(zhì)量滑塊來控制其飛行狀態(tài)。對(duì)于固定翼無人機(jī)來說，變質(zhì)心方案相對(duì)于傳統(tǒng)的氣動(dòng)舵面方案，具有維持無人機(jī)氣動(dòng)外形、提高氣動(dòng)效率、簡(jiǎn)化機(jī)翼結(jié)構(gòu)、提高隱身性能等諸多優(yōu)點(diǎn)［1］。近年來，變質(zhì)心控制技術(shù)已廣泛應(yīng)用于衛(wèi)星［2-5］、水下航行器［6-9］、高超聲速飛行器［10-14］、火星再入［15］和臨近空間飛艇［16］等多個(gè)領(lǐng)域。

當(dāng)前，對(duì)變質(zhì)心無人機(jī)的研究可分為旋翼機(jī)和固定翼兩大類。Haus等［17］著眼于控制效率，提出了一種通過質(zhì)量滑塊控制四旋翼飛行姿態(tài)的方案，將2個(gè)滑塊分別安裝在4個(gè)螺旋槳臂上，從而可以控制四旋翼的傾側(cè)和俯仰運(yùn)動(dòng)，并通過合理設(shè)計(jì)的原型機(jī)［18］，驗(yàn)證了該方案的可行性。與螺旋槳控制相比，變質(zhì)心方案具備更快的響應(yīng)速度且更為節(jié)省能量，但該方案所能提供的最大控制力矩很大程度上取決于滑塊的質(zhì)量和行程大小。對(duì)于變質(zhì)心固定翼無人機(jī)，Erturk等［19-22］做了較為系統(tǒng)的研究，沿?zé)o人機(jī)縱向和橫向分別放置滑塊，以提供操縱無人機(jī)所需的俯仰和滾轉(zhuǎn)力矩，通過分析采用該布局的變質(zhì)心固定翼無人機(jī)在平飛、零側(cè)滑角轉(zhuǎn)彎等不同工況下的特性，指出變質(zhì)心方案在不增加無人機(jī)質(zhì)量的同時(shí)，消除了傳統(tǒng)舵面方案中由于氣動(dòng)舵偏轉(zhuǎn)所引起的氣動(dòng)阻力，有效降低了無人機(jī)的燃油消耗。此外，Erturk等還考慮了螺旋槳扭矩對(duì)變質(zhì)心固定翼無人機(jī)的影響［23-24］，并開展了簡(jiǎn)單的飛行試驗(yàn)以驗(yàn)證方案可行性［25］。當(dāng)前，多數(shù)變質(zhì)心固定翼無人機(jī)采用將滑塊安裝在機(jī)翼中段的雙滑塊方案，而機(jī)翼中段狹窄的空間勢(shì)必會(huì)給滑塊的安裝帶來挑戰(zhàn)；此外，控制器多由簡(jiǎn)單的線性化方法設(shè)計(jì)［26］。顯然，對(duì)于具有強(qiáng)非線性、強(qiáng)耦合特點(diǎn)的變質(zhì)心固定翼無人機(jī)，基于線性化方法所設(shè)計(jì)的控制器在實(shí)際工作中將面臨巨大挑戰(zhàn)，甚至有失效的風(fēng)險(xiǎn)。

本文圍繞新型變質(zhì)心方案和具有強(qiáng)魯棒性的姿態(tài)控制器設(shè)計(jì)2個(gè)問題展開研究，提出了一種通過質(zhì)量滑塊控制無人機(jī)橫向運(yùn)動(dòng)的新型單滑塊方案，從而實(shí)現(xiàn)對(duì)副翼的替代。相對(duì)于雙滑塊方案［25］，該方案時(shí)滯更小、結(jié)構(gòu)更加簡(jiǎn)單，且滑塊的安裝空間相對(duì)充裕。通過對(duì)該無人機(jī)進(jìn)行動(dòng)態(tài)特性及動(dòng)力學(xué)耦合特性分析，為滑塊參數(shù)的設(shè)計(jì)提供了量化參考，給出了滑塊在機(jī)身上的理想安裝位置。基于粒子群算法（particle swarm optimization algorithm，PSO）設(shè)計(jì)了單滑塊變質(zhì)心固定翼無人機(jī)的自抗擾控制器（active disturbance rejection control，ADRC），仿真結(jié)果驗(yàn)證了該控制器具備較強(qiáng)的魯棒性和抗干擾能力。

1 運(yùn)動(dòng)模型及動(dòng)力學(xué)特性

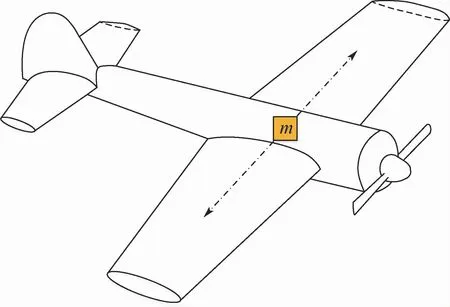
圖1 變質(zhì)心固定翼無人機(jī)簡(jiǎn)圖Fig.1 Sketch of mass-actuated fixed-wing UAV

假設(shè)圖2所示文獻(xiàn)［25］中的2種雙滑塊方案與本文的單滑塊方案具有相同的質(zhì)量比，則有μL=μR=μ1/2，μL和μR分別為雙滑塊方案中的左右滑塊質(zhì)量比。本文提出的單滑塊方案相對(duì)以上2種雙滑塊方案，具備如下優(yōu)勢(shì)：

圖2 文獻(xiàn)［25］中的雙滑塊方案Fig.2 Dual-slider scheme in Ref.［25］

1）相對(duì)于方案1，時(shí)滯更小。對(duì)于方案1來說，每次只能操縱一側(cè)的滑塊，若想提供與本文單滑塊方案相同的滾轉(zhuǎn)力矩，其滑塊的移動(dòng)距離則應(yīng)為單滑塊方案的2倍。而當(dāng)滑塊移動(dòng)速度相同的情況下，必然會(huì)導(dǎo)致方案1需要更多的時(shí)間才能提供所需俯仰力矩，即方案1的時(shí)滯更大。

2）相對(duì)于方案2，結(jié)構(gòu)更加簡(jiǎn)單。

3）滑塊的安裝空間相對(duì)充裕。由于方案1和方案2兩種雙滑塊方案均將滑塊放置于機(jī)翼中部，這對(duì)本來空間就十分狹小的機(jī)翼來說頗具挑戰(zhàn)。而本文所提出的單滑塊方案，將滑塊的移動(dòng)范圍限制在空間相對(duì)充裕的機(jī)身內(nèi)和機(jī)翼根部，這在一定程度上緩解了滑塊安裝時(shí)的空間約束問題。

1.1 變質(zhì)心無人機(jī)運(yùn)動(dòng)模型

根據(jù)牛頓運(yùn)動(dòng)定律和動(dòng)量矩定理，推導(dǎo)出本文研究對(duì)象的運(yùn)動(dòng)學(xué)模型和動(dòng)力學(xué)模型。運(yùn)動(dòng)學(xué)方程為

式中：u、v、w和p、q、r分別為無人機(jī)質(zhì)心平動(dòng)速度和繞質(zhì)心轉(zhuǎn)動(dòng)角速度在機(jī)體坐標(biāo)系三軸的分量；pn、pe、pd為無人機(jī)在地面坐標(biāo)系下的位置；φ、θ和ψ分別為滾轉(zhuǎn)角、俯仰角和偏航角。

而變質(zhì)心無人機(jī)的動(dòng)力學(xué)模型為

1.2 動(dòng)力學(xué)特性分析

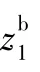
1.2.1 縱向運(yùn)動(dòng)

可以得到變質(zhì)心無人機(jī)縱向運(yùn)動(dòng)線性化方程為

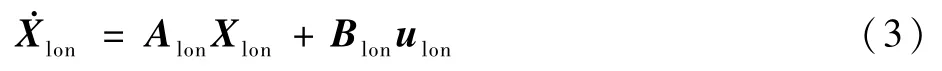
式中：Xlon=［u w q θ］T為狀態(tài)；Alon和Blon分別為狀態(tài)矩陣和控制矩陣；ulon=［δeδt］T為控制量，δe和δt分別為升降舵偏轉(zhuǎn)角和油門大小。

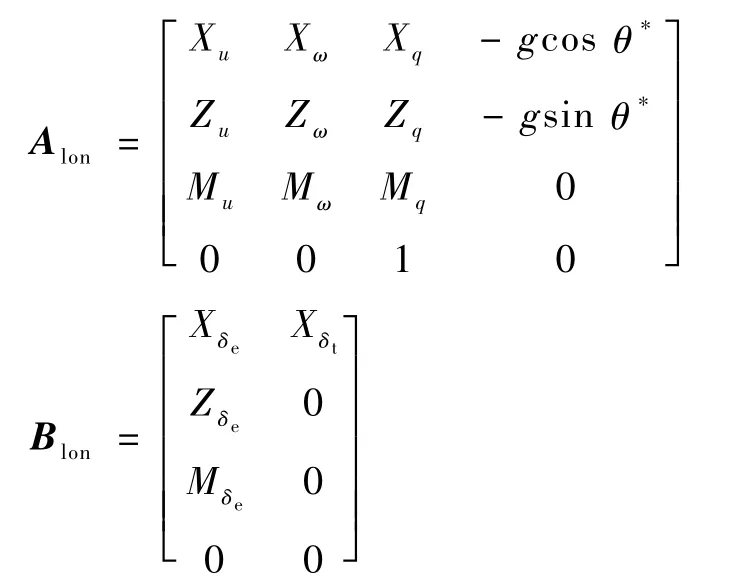
式中：矩陣Alon和Blon中各參數(shù)的具體含義見文獻(xiàn)［27］，θ*為平衡狀態(tài)下的俯仰角。

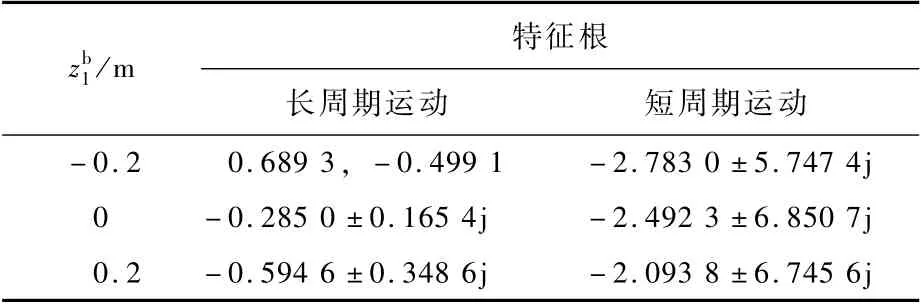
表1 縱向運(yùn)動(dòng)特征根Table 1 Eigenvalues of longitudinal motion

圖3 縱向動(dòng)態(tài)特性區(qū)域分布Fig.3 Area distribution of longitudinal dynamic characteristics

式（4）給出了變質(zhì)心無人機(jī)的俯仰力矩：

式中：G為系統(tǒng)重力；ρ為大氣密度；Sref為參考面積；c為平均氣動(dòng)弦長(zhǎng)；α為迎角；C·為各氣動(dòng)系數(shù)。

1.2.2 橫向運(yùn)動(dòng)

類似地，變質(zhì)心無人機(jī)橫向運(yùn)動(dòng)的線性化方程為

其中：矩陣Alat和Blat中各參數(shù)見文獻(xiàn)［27］，φ*為平衡狀態(tài)下的滾轉(zhuǎn)角。

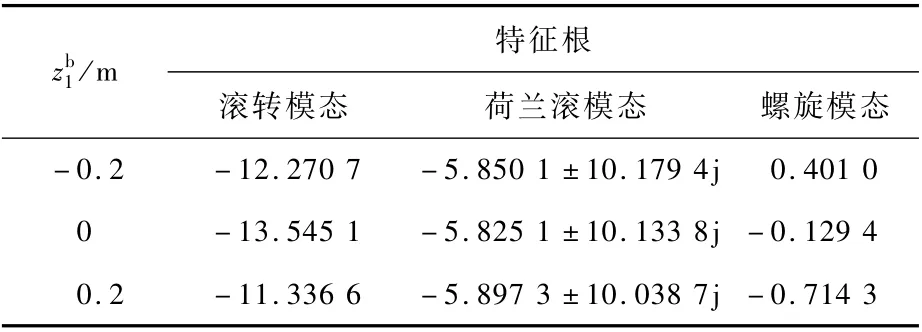
表2 橫向運(yùn)動(dòng)特征根Table 2 Eigenvalues of lateral motion

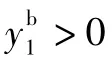
式中：k·為與發(fā)動(dòng)機(jī)性能有關(guān)的常數(shù)；b為翼展；β為側(cè)滑角。

1.3 控制效率分析

圖4給出了質(zhì)量比一定時(shí)，滑塊效率系數(shù)隨無人機(jī)飛行速度的變化曲線。可以看出，其數(shù)值隨著無人機(jī)飛行速度的增大而逐漸降低，且變化速度趨緩。因此，本文所提出的單滑塊變質(zhì)心方案適合于飛行速度普遍較低的小型固定翼無人機(jī)，可以實(shí)現(xiàn)對(duì)其姿態(tài)的高效控制。

圖4 效率系數(shù)隨速度變化曲線Fig.4 Efficiency coefficient versus airspeed

2 自抗擾控制器設(shè)計(jì)

針對(duì)變質(zhì)心無人機(jī)動(dòng)力學(xué)強(qiáng)耦合、強(qiáng)非線性特點(diǎn)，以及在飛行中面臨的參數(shù)攝動(dòng)和外部擾動(dòng)等復(fù)雜因素，本節(jié)將設(shè)計(jì)變質(zhì)心無人機(jī)自抗擾控制器。

2.1 仿射形式控制模型

令φ=［φ，θ，ψ］T、ω=［p，q，r］T，基于第1節(jié)所建立的變質(zhì)心無人機(jī)運(yùn)動(dòng)方程，可得

式中：ζ為未知擾動(dòng)；J為慣性張量；M為力矩矢量。

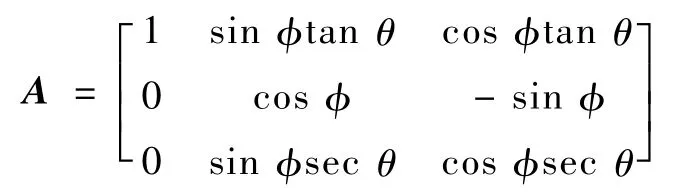
式中：

式中：dφ為總擾動(dòng)，且

2.2 控制器設(shè)計(jì)

基于式（11）所示的變質(zhì)心無人機(jī)仿射形式非線性控制模型，結(jié)合自抗擾控制器基本原理［28］，可設(shè)計(jì)如圖5所示的自抗擾控制器。

圖5 控制器結(jié)構(gòu)Fig.5 Structure of controller

首先，可設(shè)計(jì)離散形式的跟蹤微分器為

式中：r0為速度因子；h為濾波因子；φc為指令值；fhan（·）為最速綜合控制函數(shù)［28］。

擴(kuò)張狀態(tài)觀測(cè)器的離散形式為

式中：β01、β02、β03、r1、r2為可調(diào)參數(shù)，直接影響擴(kuò)張狀態(tài)觀測(cè)器的估計(jì)精度；函數(shù)fal（·）定義為

自抗擾控制器的非線性狀態(tài)誤差反饋設(shè)計(jì)為

式中：c1、r3、h1為可調(diào)參數(shù)。

進(jìn)一步動(dòng)態(tài)補(bǔ)償線性化處理，可得控制量為

考慮到所設(shè)計(jì)的控制器具有多個(gè)可調(diào)參數(shù)，手動(dòng)調(diào)節(jié)過程必然十分耗時(shí)。本文采用粒子群算法［29］對(duì)自抗擾控制器參數(shù)進(jìn)行優(yōu)化設(shè)計(jì)。根據(jù)經(jīng)驗(yàn)，跟蹤微分器的濾波因子可直接取值h=0.01，則待優(yōu)化參數(shù)為r0，β01，β02，β03，r1，r2，c1，r3，h1共計(jì)9個(gè)。利用粒子群算法優(yōu)化這9個(gè)參數(shù)時(shí)，為了在保證控制器準(zhǔn)確性和快速性的同時(shí)，防止控制量的急劇變化，將粒子的適應(yīng)度函數(shù)取值為

3 仿真分析

本節(jié)對(duì)第2節(jié)所設(shè)計(jì)的變質(zhì)心無人機(jī)自抗擾控制器進(jìn)行仿真，以驗(yàn)證控制器的有效性、魯棒性和抗干擾能力。主要分析了以下3種工況：①工況1，理想工況，系統(tǒng)無參數(shù)攝動(dòng)及外部擾動(dòng)，并將此工況作為基本參照。②工況2，變質(zhì)心無人機(jī)受到氣動(dòng)參數(shù)、質(zhì)量特性等內(nèi)部參數(shù)攝動(dòng)20%的影響，以此驗(yàn)證控制器的魯棒性。③工況3，在此工況下，第6～7 s的時(shí)間區(qū)間內(nèi)對(duì)系統(tǒng)施加一個(gè)1.5sin t形式的擾動(dòng)，用來模擬陣風(fēng)；在其余的時(shí)間內(nèi)，對(duì)系統(tǒng)施加一個(gè)0.1sin（80πt）形式的高頻擾動(dòng)，以此來驗(yàn)證控制器的抗外部干擾能力。

變質(zhì)心無人機(jī)的基本參數(shù)如表3所示。滑塊行程范圍為±0.2 m，最大滑動(dòng)速度為0.7 m/s；升降舵偏轉(zhuǎn)角限制在±30°之間；方向舵偏轉(zhuǎn)角同樣限制在±30°之間；仿真特征點(diǎn)選取為Va=40 m/s的水平直線飛行狀態(tài)。經(jīng)過粒子群算法優(yōu)化后的控制器參數(shù)為h=0.01，r0=92.123，β01=198.77，β02=5 753，β03=33 188，r1=1.331，r2=1.262，c1=1.160，r3=2.435，h1=0.086。不同工況下的控制器仿真結(jié)果如圖6～圖9所示。

表3 無人機(jī)參數(shù)Table 3 Parameters of UAV

圖6和圖7分別給出了控制器對(duì)指令姿態(tài)角的跟蹤結(jié)果及其相應(yīng)的控制信號(hào)曲線。可知，無論是面臨參數(shù)攝動(dòng)還是外部擾動(dòng)，經(jīng)過粒子群算法優(yōu)化后的自抗擾控制器，均能夠在滿足控制信號(hào)約束的條件下完成對(duì)指令信號(hào)的穩(wěn)定跟蹤，且具備良好的動(dòng)態(tài)特性及穩(wěn)態(tài)精度，這充分說明了該控制器具備良好的魯棒性和抗干擾能力。

圖6 姿態(tài)角跟蹤結(jié)果Fig.6 Tracking results of attitude angles

圖7 控制信號(hào)曲線Fig.7 Control signal curves

圖8 擴(kuò)張狀態(tài)觀測(cè)器估計(jì)誤差Fig.8 Estimation error of ESO

圖9 工況3下的擴(kuò)張狀態(tài)觀測(cè)器性能Fig.9 Performance of ESO under Condition 3

4 結(jié) 論

本文以變質(zhì)心固定翼無人機(jī)為對(duì)象展開研究，取得如下結(jié)論：

1）提出了一種時(shí)滯性更小、結(jié)構(gòu)更加簡(jiǎn)單、空間相對(duì)充裕的單滑塊變質(zhì)心固定翼無人機(jī)布局方案。

2）基于所推導(dǎo)的變質(zhì)心無人機(jī)運(yùn)動(dòng)模型，分析了滑塊參數(shù)對(duì)無人機(jī)動(dòng)力學(xué)特性的影響，并給出了滑塊在機(jī)身上的理想安裝位置。

3）針對(duì)變質(zhì)心固定翼無人機(jī)的強(qiáng)耦合、強(qiáng)非線性特點(diǎn)，本文設(shè)計(jì)了基于粒子群算法的自抗擾控制器。仿真表明，在面臨系統(tǒng)參數(shù)攝動(dòng)和外部擾動(dòng)等多種復(fù)雜工況下，該控制器均能夠有效完成對(duì)變質(zhì)心固定翼無人機(jī)的控制任務(wù)，具備良好的魯棒性。