性質教學中數學抽象素養的培養
李玲 李紅梅

[摘? 要] 數學性質的教學是培養數學抽象素養的重要載體,本質屬性的抽取,數學性質的抽象概括、數學表達、數學應用等環節都是培養數學抽象素養的良好契機. 在數學性質的課堂教學中,培養數學抽象素養的策略有:利用直觀想象,將抽象過程可視化;歸納整理知識,將抽象結果結構化;多維變式例題,將抽象結果理解深化.
[關鍵詞] 數學抽象;直觀想象;變式;數學性質
問題提出
目前,數學教育仍存在短板,一定程度上導致教育發展不均衡,從而無法切實將“立德樹人”這一根本任務落到實處,為解決這一現狀,引入數學核心素養,促使課堂教學從應試教育向素質教育過渡,打破僵硬、陳舊的教學[1]. 數學抽象素養是基本素養,也是核心素養,抽象作為基本思想,貫穿于數學概念和法則的教學[2],而性質教學是數學抽象內容的一部分. 在義務教育階段,教授者應指導學習者在性質教學中學會抽象,能夠拓展數學抽象思維,為數學抽象素養的形成做鋪墊. 本文依據圖像探究,在性質形成過程中對相關數學對象進行抽象,進一步提出對數學抽象素養的培養建議.
性質教學中數學抽象素養的培養
數學性質的學習屬于抽象性學習,學生對于這一塊的學習往往理解含糊,沒有敏捷的思維能力進行分析,無法進一步探究復雜多變的問題. 初中階段,由于學生還未形成正確的抽象意識,缺乏數學抽象思維,從而無法從基本圖像中抽象性質屬性.
1. 知識結構分析
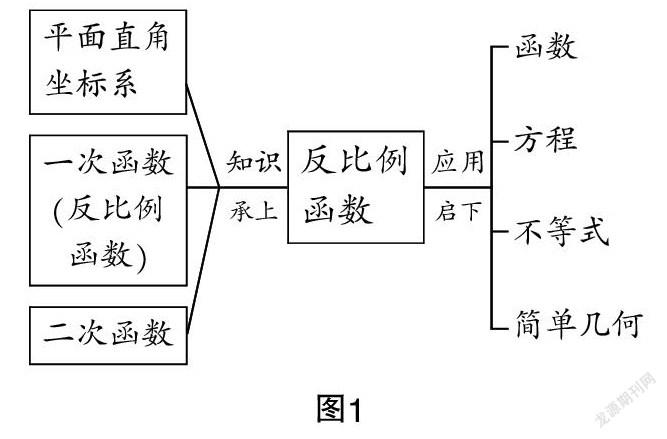
“反比例函數的圖像與性質”是人教版初中數學實驗教科書九年級下冊第二十六章第一節“反比例函數”的內容. 以該節課本主體內容為例,通過性質構建過程的逐次遞進,探析在教學中怎么培養學習者的數學抽象素養.
平面直角坐標系、一次函數和二次函數的學習在反比例函數之前,學生接續已學知識,向前邁向新的一步,“接納”新函數,聯系一次函數、二次函數性質的學習方法,通過類比慢慢轉接到對反比例函數性質的學習,認真體會新函數的內涵,充分感受由“靜”到“動”的過程[3];再者,函數性質的學習,包含了數形結合思想、建模思想,具有實踐性、探索性,為后續內容聯系、應用打下基礎.
2. 性質構建過程
數學性質形成過程中,學生應在教師的引導下不斷分析問題,逐級抽象數學性質,揭開數學知識的神秘面紗. 正比例函數是學生剛開始接觸的函數,也是突破函數性質的第一關卡,為后續函數性質的學習提供了有效的學習途徑. 正比例函數性質的學習大致通過這樣的性質構建過程:實際問題引入具體函數解析式→利用“描點”的方法作出圖像→觀察圖像并抽取函數本質特征→采用文字語言歸納和總結性質→講解例題促進學生理解性質[4]. 學生又先后學習一次函數、二次函數,具有一定的知識儲備,一是知道如何由數想形,以解析式為基礎,觀察、探析所畫函數圖像;二是探究函數性質時,需要數形結合[5],進而抽象表達出性質;三是通過觀察不同函數的圖像,知道不同函數所生成圖像的特點.
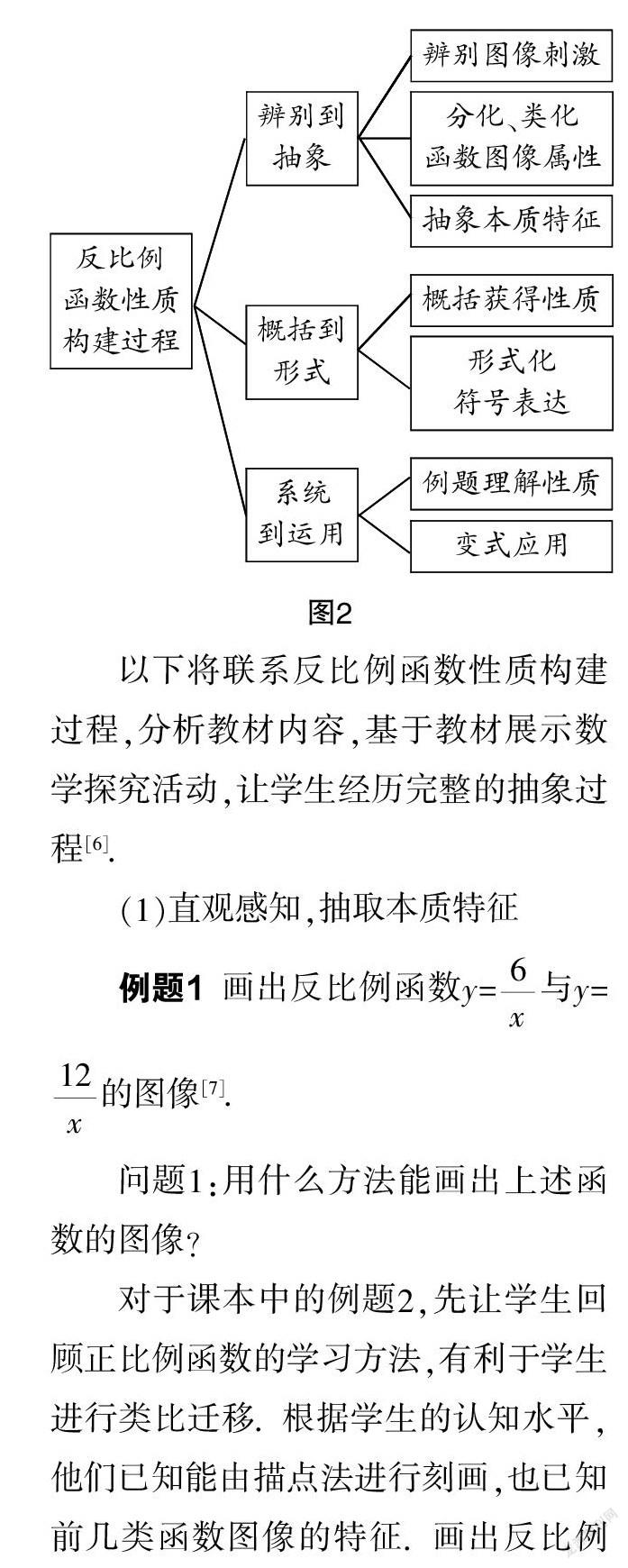
學習反比例函數性質,學生可根據先前所獲經驗,在其性質形成過程中對相關數學對象進行抽象,以利于性質的獲得. 在此以正比例函數性質構建過程為基礎,提出反比例函數的性質構建過程:
以下將聯系反比例函數性質構建過程,分析教材內容,基于教材展示數學探究活動,讓學生經歷完整的抽象過程[6].
(1)直觀感知,抽取本質特征
例題1 畫出反比例函數y=與y=的圖像[7].
問題1:用什么方法能畫出上述函數的圖像?
對于課本中的例題2,先讓學生回顧正比例函數的學習方法,有利于學生進行類比遷移. 根據學生的認知水平,他們已知能由描點法進行刻畫,也已知前幾類函數圖像的特征. 畫出反比例函數圖像后,學生可進一步觀察、分析圖像特點,以達到利用圖像的可視化進行外部刺激的效果,順利完成“辨別圖像刺激”;學生通過觀察兩個具體圖像,感知函數的性質,確定圖像形狀與所分布象限,同時發現函數值y仍隨著自變量x的變化而變化,這是學生能從正比例函數圖像和二次函數圖像中遷移過來的特征,即滿足“分化函數圖像屬性”這一步.
(2)抽象概括,獲得數學性質
問題2:觀察上述圖像,回答:
①每個函數的圖像所在象限?
②在每一個象限內,y如何由x的變化而變化?根據解析式,你能說明理由嗎?
③對于反比例函數y=(k>0),考慮①和②,得出的結論是一樣的嗎?[7]
第一,類化與抽象. ①和②的設置,可以完成數學抽象過程中的“類化”與“抽象”. 觀察兩個函數圖像,函數y=與y=的圖像均分布于兩個象限,即第一象限和第三象限,分別分析兩個象限內的函數值變化,圖像從左至右看,函數值從上到下逐漸減小. 此時利用圖形直觀的方式表現了k>0時反比例函數圖像的特點,得到他們的共同屬性:處于第一象限、第三象限與“減小”. 在類化函數圖像共同屬性的基礎上,進一步采取特殊到一般的方法,引導學生從具體例子中抽象出反比例函數y=(k>0)的基本性質.
第二,概括與表達. 對于③,是為完成數學抽象過程中的“概括”與“符號表達”,通過比較、歸納具體實例,用文字語言將關鍵詞進行串聯,概括表述性質:引導學生將圖形語言轉換為自然語言,討論自變量x與其函數值y之間的關系. 對于例題2中反比例函數y=,學生學會用自然語言描述圖像,即“函數y=的圖像在這兩個象限內,隨著x的增大,y減小”. 全體學生獲得了用文字語言描述數學性質的能力,以此為基礎,教師需要教會部分學優生用符號語言進行表述. 利用數學符號,學優生能夠描述反比例函數y=(k>0)性質中“減小”這一特點. 對于特殊函數y=,用符號語言表述“在每一個象限內,任取兩數x,x,令x
第三,類比與定義. 類比正比例函數y=kx與反比例函數y=(k>0)的性質探究,采用同樣的方法,對于k<0的情況,教師可以同學生一起定義其性質:“當k<0時,反比例函數y=的圖像位于第二象限和第四象限,每一個象限內,y隨x的增大而增大”. 轉換為符號語言“當k<0時,反比例函數y=的圖像分別位于第二象限和第四象限,那么在每一個象限內任取x,x,得y=,y=,當x
(3)歸納整理,表達數學性質
一般地,反比例函數y=的圖像是雙曲線,它具有以下性質:
①k>0時,雙曲線的兩支分別位于第一象限與第三象限,在每一個象限內,y隨x的增大而減小;
②k<0時,雙曲線的兩支分別位于第二象限與第四象限,在每一個象限內,y隨x的增大而增大. [7]
教材歸納,是為達到數學抽象階段的“理論形成”,首先,將反比例函數圖像與雙曲線相結合,有益學習者聯系新知與舊知,并促進其對知識的再認知. 再者,通過上述階段的逐級抽象,最后得到一般性結論,闡述了反比例函數的性質,以及如何表達數學性質,形成了完整的理論.
(4)例題變式,理解抽象結果
例題2 已知反比例函數y=圖像的一支(如圖5). 問:①圖像的另一支在哪個象限?常數m的取值范圍是什么?②在圖像的一支上隨意取點A(x,y)和點B(x,y),若x>x,那么y和y有怎樣的大小關系?[7]
這個題目是為了了解學生對數學性質的理解與運用程度. 對于問題①,學生通過討論圖像分布象限,探究m的取值范圍,實質是對反比例函數中k的討論;對于問題②,學生已知圖像的分布,可直接根據性質定義判斷得到在每一個象限任取x,x,當x>x,都有y 變式1:已知反比例函數y=過點A(-2,-1),m的值是多少?圖像位于哪些象限? 變式2:點A(2,y),(5,y)在反比例函數y=上,比較y和y的大小. 變式3:已知反比例函數y=,問:①探究常數m的取值范圍,觀察此時函數圖像的分布情況. ②在圖像某一支上任取兩點M(x,y),N(x,y),若x 變式1簡單改變函數解析式,將例題中給出圖像變化變為給出點坐標,引導學生通過點的坐標求解問題;變式2通過判斷m2+3的值與0的關系確定圖像所在象限,再根據給出的不同x值對相應y值進行比較,需要注意此題無關具體關系式的求解;變式3需要學生綜合考慮,分類討論m-5的符號,進而解答疑問. 例題及變式的設置,是為了“理解”與“應用”. 學生學習新知,教師需要綜合教材內容與學生學情,通過逐次遞進的變式,引導學生探究知識的“來龍去脈”[8]. 兩個例題的設置均以反比例函數圖像性質為中心,突出其本質,利用性質定義解題,學生能對學習內容有更清晰的理解,實現學習目標. 再者,上述變式通過例2進行衍生,促使學生更好地理解本節知識,更好地掌握抽象結果. 通過變式,學生在反比例函數性質的學習構建過程中,多角度思考問題,知道在問題解決過程中從圖像出發,但不局限于用圖像解決問題,從而理解從圖像中所抽象出來的性質,學會運用性質定義,同時,掌握相關數學方法,積累數學經驗. 教學建議 基于對性質教學中具體數學內容的探析,筆者給出三個教學建議. 1. 利用直觀想象,將數學抽象過程可視化 直觀想象是數學抽象的基礎,采用直觀手段,學生進一步借助直觀進行想象,有利于學生進行數學抽象,從感性認識上升到理性認識. 通過數學抽象的過程,學生直觀感知,察看、分解問題,領會所學知識,解決問題:首先,積極思考,主動參與學習探究,分析所提供的直觀材料,從圖像中抽取事物的本質特征;其次,結合信息技術教學,學生體會圖形的動態變化過程,簡化題設中的問題;最后,從數學抽象中明白將實質問題轉化為數學問題,形成正確認識. 教師應充分調動學生的直觀認知,引導學生有意識地利用直觀想象探究知識的產生與發展,使學生有效掌握抽象事物的形成過程,逐漸形成數學抽象素養. 2. 歸納整理知識,將數學抽象結果結構化 知識結構展示了相關知識間的內在聯系,給予學生清晰的知識線,歸納整理知識結構,有利于知識系統化、知識整體化、知識簡易化. 數學抽象素養蘊含在豐富的教學內容中,這就要求教師在教學中幫助學生厘清知識間的脈絡,獲得抽象方法,利用圖示促使學生理解記憶. 新知的學習是在舊知的鋪墊下進行的,學生應當學會“讀”材料,“析”材料,注意抽象知識之間的層次分節,同化或順應知識,表達數學抽象結果,納入相關知識系統,將其結構化,促進自身的思維訓練,這有利于知識之間的正遷移,對其他具體數學內容也能進行逐級抽象. 如本文對反比例函數性質的學習,接續對變量、函數的初步了解,以及對其概念的掌握,更深層次地基于圖像抽象性質,為之后學習各類函數提供了基礎方法,同時,廣泛應用于函數、方程、不等式中. 3. 多維變式例題,將數學抽象結果理解深化 例題構成了教學內容,是不可或缺的一部分,是對某一知識具體運用的體現,較為集中地體現了其特點、思想和要領等,淺顯易懂地呈現在學生眼前. 學生通過解答例題,能夠熟悉概念定義、公式定理等,明晰相關符號語言的表示意義,形成正確的知識體系,突出數學對象的本質. 對例題的變式,能夠加強知識間的關聯性,串聯零散的知識點,讓學生感受知識生長過程的同時,可以多維度強化數學知識,感知數學抽象素養,提高認識力,促進他們對數學抽象結果的深化理解. 此外,進行知識教學,應避免“解題教學”,變式以例題為基準,設計以本堂課中心內容為主線、以學生理解抽象結果為目標的問題,并非強調解題技巧、解題速度. 結束語 本文以反比例函數為例,利用直觀想象、歸納整理和例題變式等活動開展教學,將抽象過程可視化,抽象結果結構化,使學生的數學理解深刻化,從而展現性質教學中數學抽象素養的培養過程. 這一知識構建過程適用于數學性質教學,如一次函數的性質、二次函數的性質等. 當然,根據實際教學情境的不同,具體教學設計也應有所變化,例如在直觀想象的過程中,僅從圖像角度進行教學設計有其局限性,抽象過程可視化的方法還有很多,還有待進一步研究. 參考文獻: [1] 錢瑤強. 基于數學核心素養下的高效課堂教學的策略研究[J]. 數學教學通訊,2021(12):43-44. [2] 中華人民共和國教育部. 義務教育數學課程標準(2011年版)[M]. 北京:北京師范大學出版社,2012. [3] 羅增儒. “反比例函數”的課堂研修[J].中學數學教學參考,2020(08):12-17. [4] 黃欲涵.概念自然生成,實踐分析特性——以“正比例函數”的教學為例[J].數學教學通訊,2018(23):59-60+67. [5] 毛大平,應佳成. 為學生的數學理解而教——“一次函數的圖象”教學設計[J].中國數學教育,2020(23):13-17. [6] 鄧翰香,吳立寶,沈婕. 指向數學抽象素養的教材分析框架與案例剖析——以人教A版“函數單調性”為例[J]. 數學通報,2019,58(10):33-38. [7] 人民教育出版社. 義務教育教科書數學九年級下冊[M]. 北京:人民教育出版社,2018. [8] 馬志洲. 構建深度學習課堂,促進數學核心素養的養成——以“反比例函數等積模型”教學為例[J]. 數學教學通訊,2020(20):27-28+75.

