基于粒子群優化機器學習模型的水面蒸發量估算模型研究

楊 環

(江西省贛西土木工程勘測設計院，江西 宜春 336000)

水面蒸發量是反映全球水循環變化趨勢的重要指標之一，其值的準確估算可方便對大氣蒸散數據的獲取，對解決區域水資源問題有著重要的意義[1- 2]。目前，常以蒸發皿蒸發量(Epan)表征區域水面蒸發量的數值[3- 4]。由于實際觀測條件的限制，對于Epan數據的準確測量無法滿足區域時間和空間上的要求，因此，對水面蒸發實測值全國仍有很多區域未覆蓋到[5]。因此，通過氣象數據估算區域Epan數值成為了各部門研究的熱點，例如PenPan模型[6]、Stephens and Stewart(SS)模型[7]等。這些模型在不同氣候區表現出的精度有所差異，因此，找尋適用于不同區域的Epan準確估算模型對研究區域水資源平衡具有十分重要的意義。

隨著計算機技術的不斷發展，機器學習模型已被逐漸應用于Epan數值預測中[8]。Kim等[7]采用多層感知器-神經網絡(MLP-NN)、廣義回歸神經網絡(GRNN)和支持向量機-神經網絡(SVM-NN)對不同區域日Epan進行了模擬，指出SVM-NN模型精度高于MLP-NN和GRNN模型；龍亞星等[9]基于前饋人工神經網絡構建了陜北、關中和陜南Epan估算模型，指出該模型在不同區域的精度有所差異。

雖然機器學習模型在Epan數值預測中已取得了一定的進展，但傳統的機器學習模型往往存在局部極值的問題，導致模型在不同區域的精度存在差異[10]。為進一步提高機器學習模型的精度，本文基于BP神經網絡、極限學習機(ELM)、隨機森林(RF)、支持向量機(SVM)4種傳統機器學習模型，采用粒子群算法(PSO)進行優化，得出4種優化模型，以江西省為研究區域，構建適用于江西省Epan預測的最優模型。

1 研究區域與數據來源

江西省(N24°29′14″～30°04′41″，E113°34′36″～118°28′58″)地處華東地區，屬亞熱帶季風氣候。省內降水較多，多年平均降水量達到了1630mm，溫度適中，年平均氣溫11.6～20℃[11]，全省冬暖夏熱，對該省Epan的研究對長江流域的發展有著十分重要的作用[12]。本文選擇江西省景德鎮、南昌、井岡山等15個氣象站點1980—2020年的逐日氣象數據和實測Epan數值，氣象數據來自國家氣象中心網站，數據質量控制良好，研究區域概括及站點分布如圖1所示。

圖1 研究區域概況圖

2 研究方法

2.1 粒子群算法

Eberhart和Kennedy于1995年首先提出粒子群算法(PSO)[13]。該算法基于群鳥喂養的原則，將整個鳥群視為粒子群，每只鳥定位一個粒子。每個粒子均有運行速度，這個速度決定了粒子在多維搜索空間中運動的方向和距離，這個速度受粒子慣性的影響[14]。在每次迭代過程中，粒子群算法通過個體極值Pbest和全局極值Gbest更新其速度和位置，在滿足預定的準則后，跳出迭代，得到最優解，具體步驟可見文獻[15]。

2.2 極限學習機模型

極限學習機模型(ELM)有助于克服傳統神經網絡收斂速度慢的缺點，在回歸檢驗和模型預測領域得到了廣泛的應用[16]。該模型可分為三個部分：輸入層、隱含層和輸出層。首先，變量通過輸入層輸入，然后通過輸出層輸入，權值為βjk。輸出變量矩陣采用隱層權值ωij計算。

2.3 支持向量機模型

支持向量機模型(SVM)最早由Vapnik在1999年提出[17]。該模型被認為是目前小樣本統計估計和預測學習的最佳理論。該模型用結構經驗最小化取代了傳統的經驗最小化，克服了神經網絡的許多缺點。SVM函數可以表示為：

(1)

式中，κ(xi，xj)—由輸入向量xi和xj轉換而來的高維特征向量；yi—輸入向量的坐標；αi—輸入向量的權值；b—偏差。

2.4 BP神經網絡模型

BP神經網絡模型(BP)是一種具有誤差反向傳播功能的多層前饋神經網絡模型，該模型包括信號正傳播和誤差的反向傳播2部分。BP模型由輸入層、隱含層和輸出層3部分組成，原始信號經由隱含層，由輸入層向輸出層傳播，若輸出結果不滿足誤差要求，則錯誤信號由隱含層返回輸入層，基于梯度下降法調整模型權重及閾值，直至輸出結果滿足誤差要求為止。具體模型步驟可見文獻[18]，模型基本原理如圖2所示。

圖2 BP神經網絡結構圖

2.5 隨機森林模型

RF模型由Breiman[19]在2001年提出。該模型在模型訓練過程中引入了隨機屬性選擇。該模型基于隨機性和差異性提取數據，大大提高了決策的準確性。RF模型步驟可見文獻[19]。

2.6 模型訓練與驗證

由于溫度數據是氣象數據中最易獲得的數據，因此，本文采用Tmax和Tmin作為輸入數據訓練模型，采用1980—2010年的數據訓練模型，2011—2020年的數據預測模型，模型精度指標選擇均方根誤差(RMSE)、決定系數(R2)、平均絕對誤差(MAE)和效率系數(Ens)4個指標評價不同模型精度，公式如下：

(2)

(3)

(4)

(5)

引入GPI指數，整合4個指標的綜合評價結果，公式為：

(6)

式中，αj—常數，計算MAE和RMSE時取1，Ens和R2取-1；gj—不同指標的中位數；yij—不同指標的計算值。

3 結果與分析

3.1 不同站點Epan日值精度對比

圖3為不同模型對Epan日值的模擬精度對比。由圖中可以看出，經PSO算法優化后的模型精度要高于傳統的4種機器學習模型。其中，PSO-RF模型的精度最高，PSO-ELM模型精度次之，2種模型Ens、R2、RMSE、MAE的中位數分別為0.900和0.849、0.935和0.895、0.232mm/d和0.319mm/d、0.604mm/d和0.809mm/d。未經優化的傳統模型中，ELM模型精度最高，其Ens、R2、RMSE、MAE的中位數分別為0.820、0.827、0.569mm/d、1.031mm/d。BP模型在所有模型中的精度最低，模型在整個江西省的誤差較高，同時與實測值的一致性較低。從GPI箱線圖中可以看出，PSO-RF模型的GPI最高，其次為PSO-ELM、PSO-SVM、PSO-BP模型，4種模型的GPI中位數分別為1.243、0.949、0.640、0.480，BP模型精度最低，GPI中位數僅為-0.220，建議使用PSO-RF模型估算江西省Epan日值。

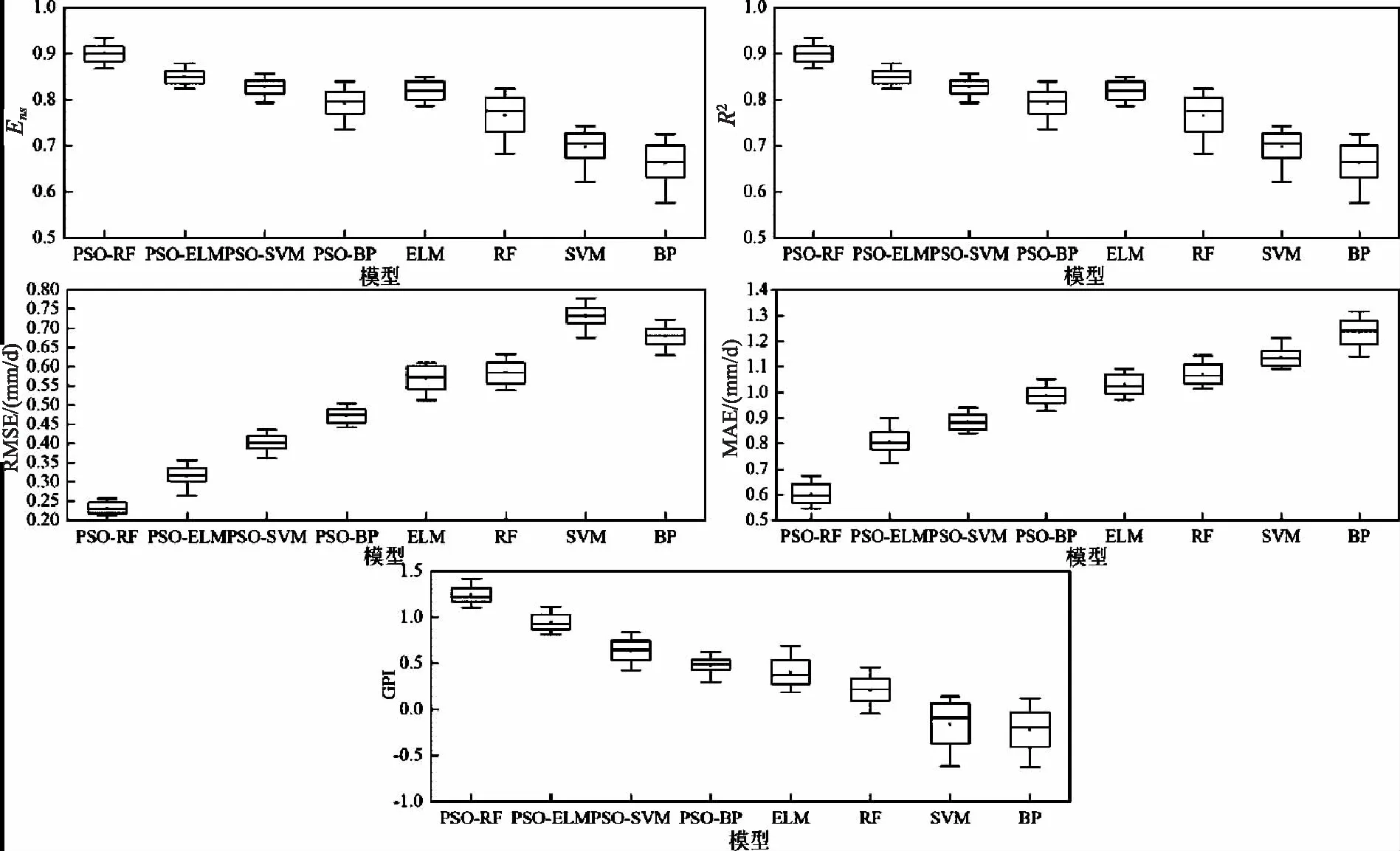
圖3 不同模型Epan日值精度對比

3.2 不同站點Epan月值精度對比

圖4為不同模型對Epan月值的模擬精度對比。由圖中可以看出，在模擬Epan月值時經PSO算法優化的模型精度普遍較高，PSO-RF模型精度最高，其Ens、R2、RMSE、MAE的中位數分別為0.935、0.967、0.077mm/d、0.063mm/d，未經優化的傳統模型中，ELM模型精度最高，其Ens、R2、RMSE、MAE的中位數分別為0.827、0.913、0.304mm/d和0.303mm/d，BP模型精度較低，Ens、R2、RMSE、MAE的中位數分別為0.560、0.830、0.413mm/d和0.629mm/d。從GPI箱線圖中可以看出，PSO-RF模型的GPI最高，達到了2.655，未經PSO算法優化的模型GPI較低，ELM、RF、SVM、BP模型的GPI分別僅為0.085、-0.639、-0.906、-1.621，因此，PSO-RF模型估算江西省Epan月值精度最高。

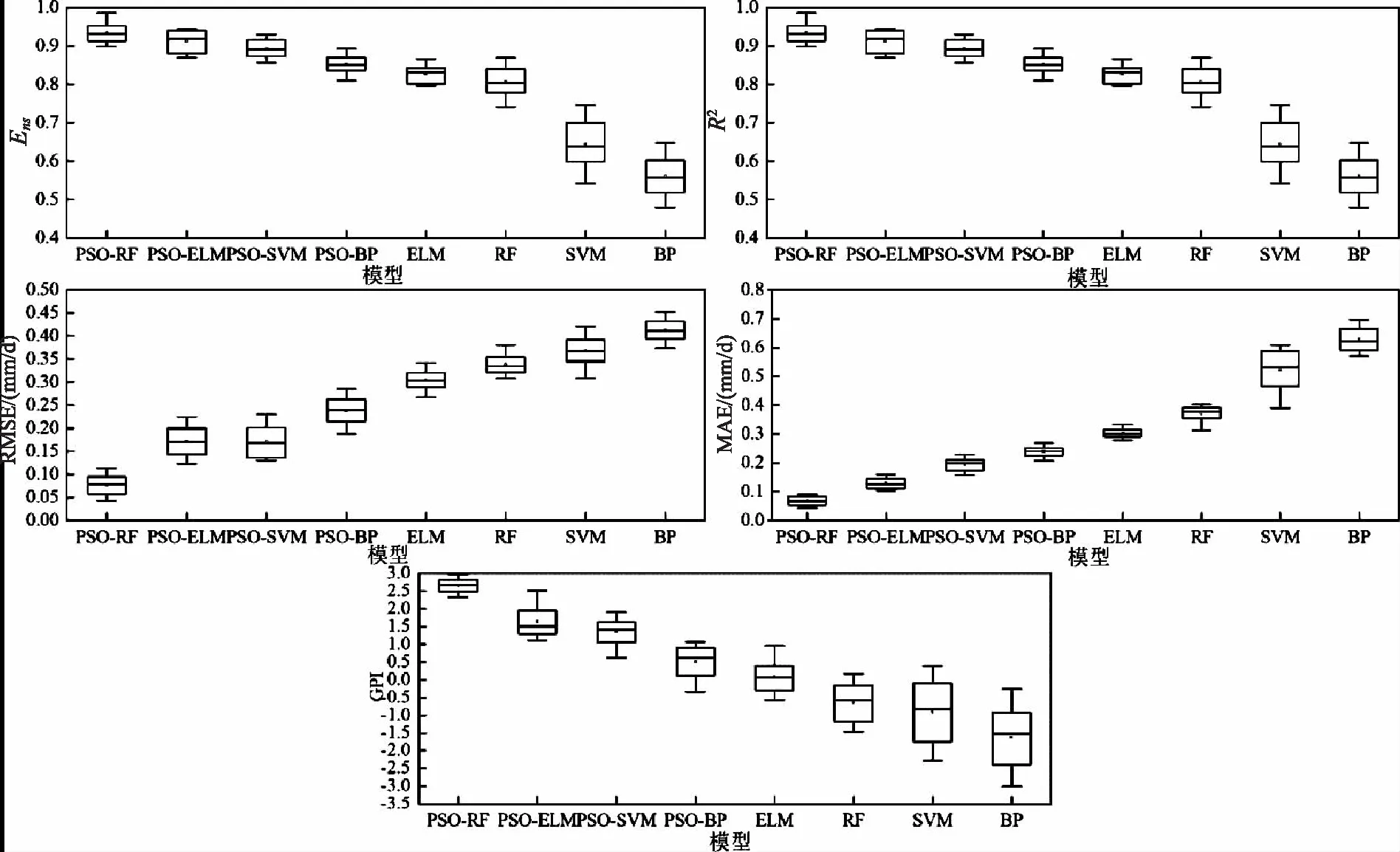
圖4 不同模型Epan月值精度對比

3.3 不同時段不同模型Epan相對誤差對比

圖5為不同模型在不同時段Epan估算的相對誤差對比。由圖中可以看出，在不同時期不同模型的Epan相對誤差存在差異。在冬季，不同模型的相對誤差較低，PSO-RF模型的相對誤差最低，僅為10.8%，BP模型相對誤差最高，隨著氣溫的升高，在夏季不同模型的相對誤差均高于其他季節。從主要作物生長期的3—10月和全年來看，PSO-RF模型的相對誤差在4.1%～4.4%。在不同時期，均表現為PSO-RF模型的相對誤差最低，推薦該模型作為江西省Epan的估算模型。

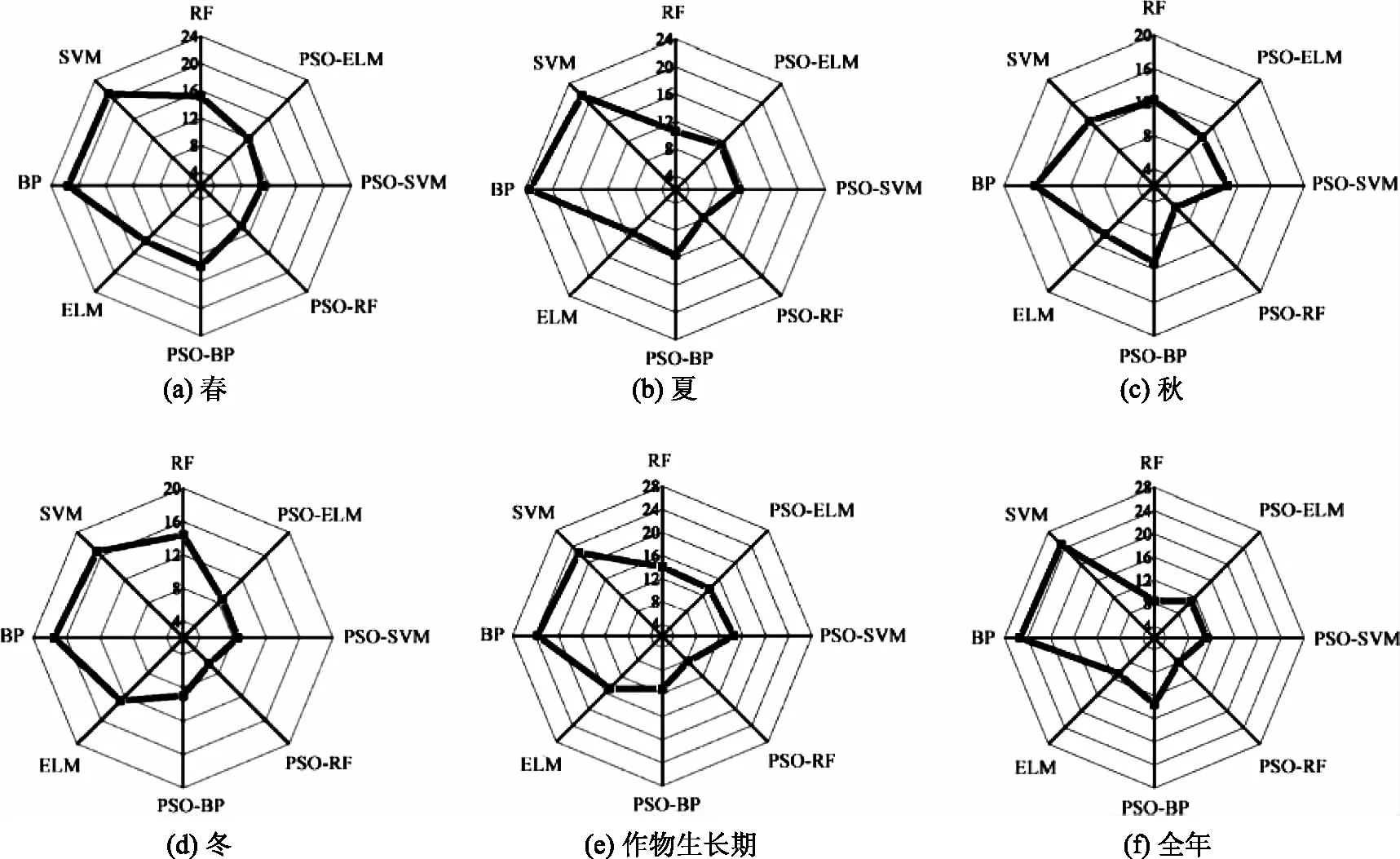
圖5 不同時段不同模型Epan相對誤差分布

3.4 PSO-RF模型可移植性分析

為進一步證明PSO-RF模型的精度，本文對該模型在江西省的可移植性進行了分析，結果見表1。由表中可以看出，對不同訓練組合和預測組合下，該模型均表現出了較高的精度，Ens和R2均在0.92以上，RMSE和MAE均在0.127mm/d以下，精度較高。見表1。

表1 PSO-RF模型可移植性分析結果

4 結語

(1)對不同模型對Epan日值的精度進行對比分析，發現經PSO算法優化的模型精度普遍優于傳統機器學習模型，其中以PSO-RF模型精度最高，BP模型精度最低；在對Epan月值進行模擬時發現了相同的結論。

(2)對不同時期不同模型Epan估算的相對誤差進行分析，發現不同時期模型計算精度有所差異，其中冬季模型精度最高，PSO-RF模型在全年和作物生長期的相對誤差為4.1%～4.4%，精度最高。

(3)對PSO-RF模型的可移植性進行了分析，指出在不同組合下，該模型仍能保持較高的計算精度，因此，PSO-RF模型可作為江西省水面蒸發的估算模型使用。

(4)本文基于PSO算法優化的機器學習模型對江西省水面蒸發進行了估算，指出了該算法可顯著提高傳統模型精度，遺傳算法、貝葉斯理論均可用于優化機器學習模型，不同優化算法的精度差異可在后續進一步研究討論。