兩個圈笛卡爾乘積的羅馬控制數

胡夫濤，于紫嫣，孫美鈺

安徽大學數學科學學院，安徽 合肥 230601

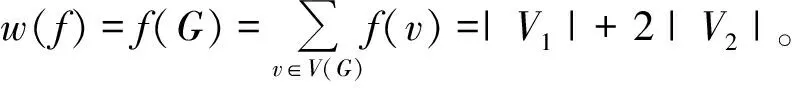
圖的控制數的研究歷史可追溯到公元1850年。圖的控制問題和相關子集問題的研究是圖論研究中心熱點，引起了人們廣泛的研究，相關研究成果詳見專著[2-5]。在圖的控制論中，圖的羅馬控制數問題是一個基本問題，并且具有數學和歷史的雙重意義。REVELLE[6]在1997年介紹了羅馬控制問題；IANSTEWART[7]在1999年討論了君士坦丁為保衛羅馬帝國而采取的策略，并提出一個新的控制數，即羅馬控制數；COCKAYNE等[8]給出了圖中羅馬控制的定義；此外，還有很多的羅馬控制相關結果，例如文獻[9，10]。圖論研究中染色問題研究(文獻[11])和圖的控制有很相似的地方，圖論研究也有很多重要的應用[12]。

2個圖的笛卡爾乘積是構造大的圖模型的重要工具。人們對常見的網絡，如路和路、路和圈、圈和圈的笛卡爾乘積，都有很深入的研究，在圖的控制數方面有很多研究成果：文獻[13]研究了路和圈的笛卡爾乘積的成對控制數；文獻[14]研究了圈和圈的全控制數和成對控制數；文獻[15]給出了一個算法求解圈與圈笛卡爾乘積的羅馬控制數精確值。對正整數n≥3，筆者通過嚴格的理論證明確定了P2×Cn,C3×Cn,C4×Cn,C5×Cn的羅馬控制數精確值和G6,n的羅馬控制數上界。

1 基本性質

引理 1[8]對任意圖G,γ(G)≤γR(G)≤2γ(G)。

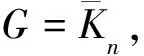
引理3[8]設f=(V0,V1,V2)是任意γR-函數，則：

1)G[V1],V1的子圖最大度為1；

2)V1和V2在G中無邊；

3)V0中的點最多連接V1中2個點；

4)V2是G[V1∪V2]的一個控制集。

引理4[8]設G是階為n的連通圖，則γR(G)=γ(G)+1當且僅當V中一點v的度為n-γ(G)。引理5[8]任意圖G的階為n，最大度為Δ，則：

2 主要結果

設Cn和Pn分別表示為階為n的圈和路，且它們的頂點集記為：

V(Cn)=V(Pn)=[n]={1,2,…,n}

記Gm,n=Cm×Cn為2個圈Cm和Cn的笛卡爾乘積，設它們的頂點集為：

V(Cm×Cn)=V(Pm×Cn)={vi,j:1≤i≤m,1≤j≤n}

對任意j∈[n]，記：

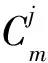
2.1 P2×Cn的羅馬控制數精確值

定理1設正整數n≥3，則:

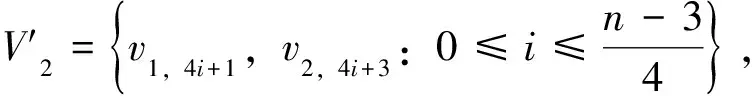
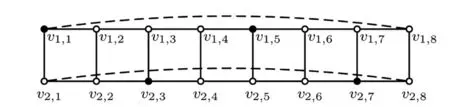
注：黑實心點函數值為2，空心點函數值為0。圖1 構造的P2×C8的羅馬控制函數Fig.1 Constructed RDF of P2×C8

易見f=(V0,V1,V2)是P2×Cn的一個羅馬控制函數，其中V0=V(P2×Cn)(V1∪V2)。因此：

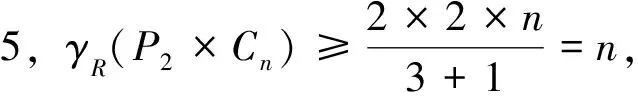
利用反證法，假設存在P2×Cn的一個γR-函數f=(V0,V1,V2)，使得γR(P2×Cn)=2|V2|+|V1|=n。因為V2中的一個點最多控制3個V0中的點，所以4|V2|+|V1|≥V(P2×Cn)=2n，從而得到4|V2|=2n，且|V1|=0。因此每個V2中的點都與V0中的3個點鄰接，且V0中每個點只與V2中唯一一點鄰接。根據對稱性，不妨設v1,1∈V2，則v2,3∈V2，對應v1,5∈V2，如此下去總會得到v1,n∈V2或者v1,n與V2中2個點相鄰，得到矛盾。因此當n≡1,2,3(mod 4)時，γR(P2×Cn)=n+1。

綜上，有：

2.2 G3,n的羅馬控制數精確值

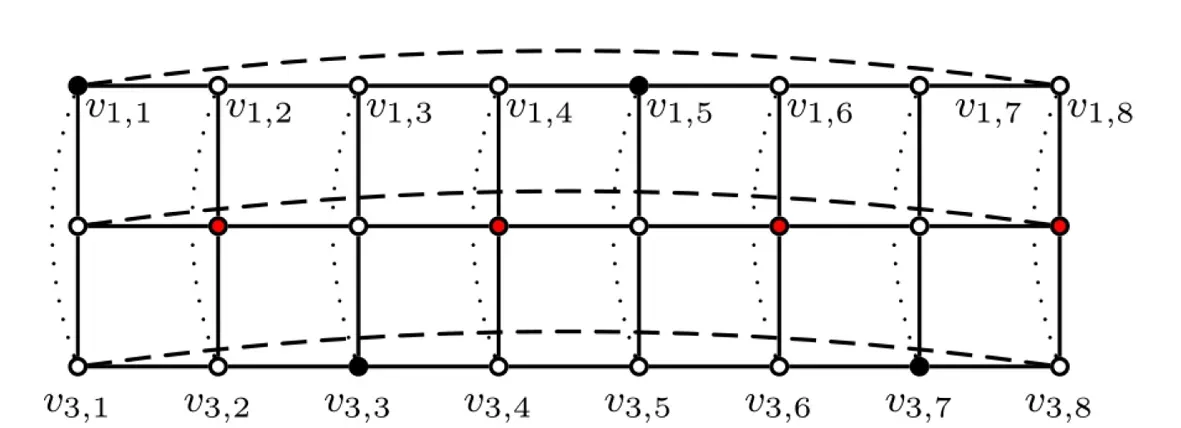
注：黑實心點函數值為2，紅實心點函數值為1，空心點函數值為0。圖2 構造的G3,8的羅馬控制函數Fig.2 Constructed RDF of G3,8

易見f=(V0,V1,V2)是G3,n的一個羅馬控制函數，其中V0=V(G3,n)(V1∪V2)。因此：

所以：

2.3 G4,n的羅馬控制數精確值

定理3設正整數n≥3，則γR(G4,n)=2n。

證明設：

V2={v1,i,v3,j:i=0(mod 2),j=1(mod 2),i,j∈[n]}V1=φV0=V(G4,n)(V1∪V2)

則易見f=(V0,V1,V2)是G4,n的一個γR-函數，從而γR(G4,n)≤2n。圖3為構造的G4,8的羅馬控制函數。

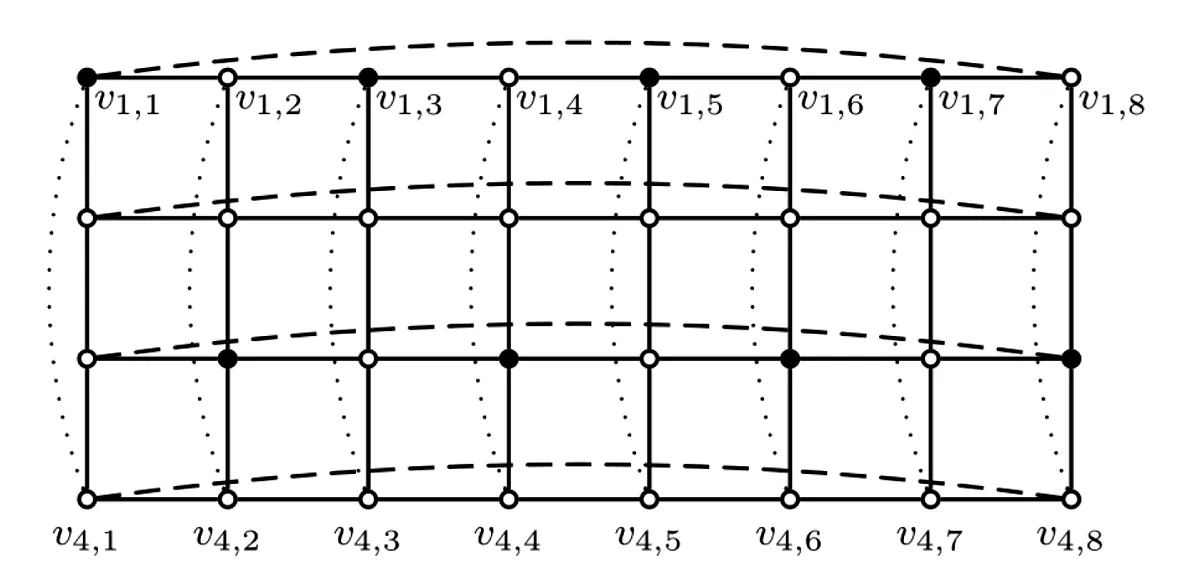
注：黑實心函數值為2，空心點函數值為0圖3 構造的G4,8的羅馬控制函數Fig.3 Constructed RDF of G4,8

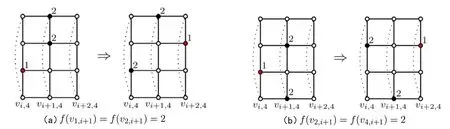
圖4 |V2∩|=2且f(v2,i+1)=2時的重新賦值Fig.4 Reassign when |V2∩|=2 and f(v2,i+1)=2

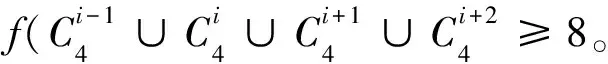
所以：

γR(G4,n)=2n

2.4 G5,n的羅馬控制數精確值

性質1設正整數n≥3和l≥1，則：

γR(G5l,n)=2ln,n≡0(mod 5)

γR(G5l,n)≤2ln+2l,n≡1,2,3,4(mod 5)

證明設：

v8,p,…,v5l-2,p,v1,q,v6,q,…,v5l-4,q:i≡1(mod 5),j=2(mod 5),k≡3(mod 5),p≡4(mod 5),q≡4(mod 5)}

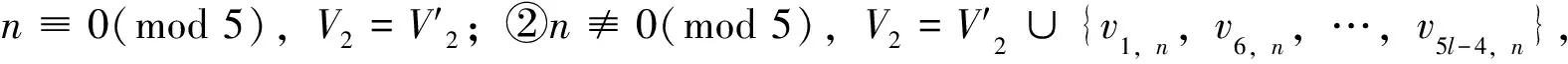
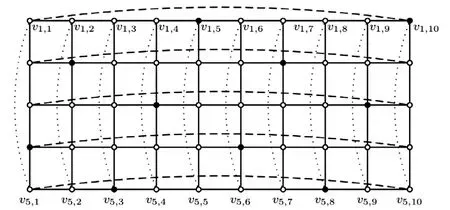
注：黑實心點函數值為2，空心點函數值為0。圖5 構造的G5,10的羅馬控制函數Fig.5 Constructed RDF of G5,10

因此：

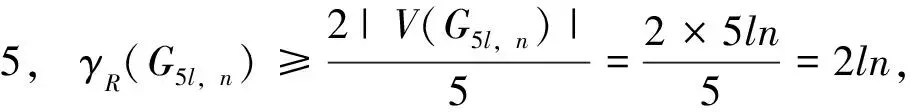
定理4設正整數n≥3，則:

證明根據性質1，有：

γR(G5,n)=2n，n≡0(mod 5)

γR(G5,n)≤2n+2，n≡1,2,3,4(mod 5)

因此只需考慮n?0(mod 5)的情形。

設f=(V0,V1,V2)為G5,n的所有γR-函數中|V1|數最小的，其中f=2|V2|+|V1|，根據定義：

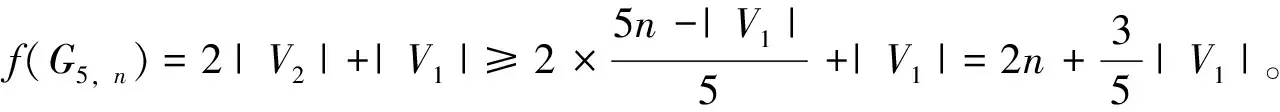
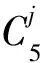
V2={v4,i,v2,j,v5,k,v3,p,v1,q:i≡1(mod 5),j≡2(mod 5),k≡3(mod 5),p≡4(mod 5),q≡4(mod 5)}

當n?0(mod 5)時，v1,n?V2，此時v1,1∈V0不與任何V2中的點相鄰，矛盾。

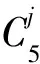
V2={v4,i,v2,j,v5,k,v3,p,v1,q:i≡1(mod 5),j≡2(mod 5),k≡3(mod 5),p≡4(mod 5),q≡4(mod 5)}

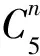
2.5 G6,n羅馬控制數上界

定理5設正整數n≥6，則:

證明設：

k≡3(mod 6),p≡4(mod 6),q≡5(mod 6),r≡0(mod 6)

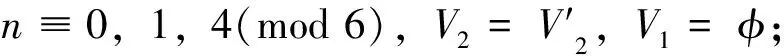
注：黑實心點的函數值為2，空心點的函數值為0。圖6 構造的G6,8的羅馬控制函數Fig.6 Constructed RDF of G6,8

G6,n的羅馬控制數上界是可以達到的，因為里面涉及的情況非常多，在以后的研究中將進一步考慮其它Gm,n未確定的羅馬控制數。