多周期穩定數值造波的參數設計方法

呂磊，陳作鋼

1 上海交通大學 海洋工程國家重點實驗室，上海 200240

2 高新船舶與深海開發裝備協同創新中心，上海 200240

3 上海交通大學 船舶海洋與建筑工程學院，上海 200240

0 引 言

在船舶與海洋工程領域，利用計算流體力學（CFD）方法研究波浪中結構物的各類響應一直是重要的研究方向。然而，在進行CFD計算時，數值模擬收斂需要一定的物理時間，但數值波在計算過程中會發生波幅衰減和相位偏差的問題，影響結構物響應的計算精度。因此，實現多周期穩定的數值造波顯得尤為重要。

目前，較為常用的數值造波方法為有限體積法（finite volume method，FVM），通過求解雷諾平均（Reynolds averaged Navier-Stokes，RANS）數值方程，并結合流體體積（volume of fluid，VOF）多相流模型來模擬波浪傳播過程。對于此類數值造波問題，國內學者進行了廣泛研究。例如：楊云濤等[1]基于不可壓縮黏性流體的Navier-Stokes方程，采用質量源造波法（mass source-based wave generation）建立了三維無反射數值波浪水池，克服了邊界造波法無法消除二次反射波的困難，并成功模擬了波浪與浮體相互作用的問題。王東旭等[2]選擇兩相不可壓縮黏性流求解器 InterFoam作為平臺進行了數值波浪水槽的開發，使用動邊界造波法和質量源造波法進行了規則波和不規則波的模擬計算，結果表明，所開發的數值波浪水槽具有較高的精度與良好的造波能力。余陽等[3]基于推板造波理論和搖板造波理論，在Open-FOAM平臺上采用重疊網格技術建立黏性數值波浪水槽，對比研究了此數值模型分別嵌入層流和湍流兩種模型后的計算精度及效率，并對三維數值造波問題進行了進一步研究，驗證了在三維兩相流體域中求解運動物體與流場交互的可靠性和正確性。上述研究從各方面探討了數值造波問題，并發現數值波在傳播過程中普遍存在波幅衰減和相位偏移的現象。總之，包括網格設置在內的多個參數共同影響了數值造波的精度，而對于數值造波誤差的評估及造成誤差的關鍵參數仍缺乏定量的系統性研究。

因此，本文將基于STAR-CCM+商業求解器進行數值模擬，以五階Stokes波作為研究對象，首先將CFD計算結果與理論解進行對比，通過對一維波動方程的離散形式的分析，得到影響造波精度的幾個關鍵參數，進一步研究這些參數對造波效果的影響。然后，通過算例計算，驗證內迭代次數的選擇、網格分辨率的設置及庫朗數等對波幅衰減和相位偏移的影響，并合理選擇參數來顯著提高多周期造波精度，最后，總結得出一套合理的參數設計方法，基于此方法，以KCS(KRISO container ship)船型為例，模擬計算其在迎浪中阻力和運動響應，再通過與實驗數據的對比，以驗證本文參數設計方法的可行性。

1 數學模型

1.1 控制方程

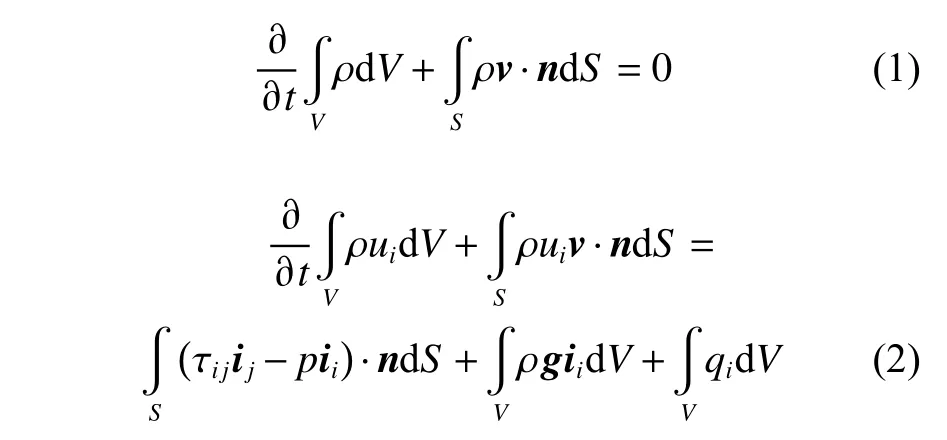
計算的控制方程為Navier-Stokes方程，包括連續性方程和動量守恒方程，如式（1）和式（2）所示。式中：V為控制體；S為控制體的邊界；v為流體的速度矢量；ui速度矢量的笛卡爾分量；n為垂直于邊界S并指向邊界外的單位矢量；t為時間；p為壓力；ρ為流體的密度；τij為黏性應力張量的分量；ii和ij分別為xi方向和xj方向的單位矢量；g為體積力，在此即為重力；qi為一個可選的動量源項，將在之后的消波設置中具體說明。

1.2 湍流模型

在對多周期的波浪進行數值模擬時，隨著計算物理時間的增加，自由液面處的湍流黏度急劇升高，此時會對波幅產生削減作用，且不同湍流模型對波浪傳播產生的負面影響也不盡相同。因此，本文使用標準的低雷諾數K-Epsilon模型，將其中的湍動能和湍流耗散率設為非常低的初始值，這會有助于改善湍流黏度對波浪傳播的不利影響[4]。本文所有算例也均采用該K-Epsilon模型，根據文獻[4] 湍動能和湍流耗散率的初始值分別設為：1×10?5J/kg和1×10?4m2/s3，與默認值相比分別小了2和3個數量級。

1.3 自由液面捕捉

使用VOF法追蹤流體自由液面的位置。該方法使用流體體積比ai表 示第i相流體在網格單元中所占的體積分數。每個網格單元中的體積分數ai之和必須等于1。體積分數的輸運方程為

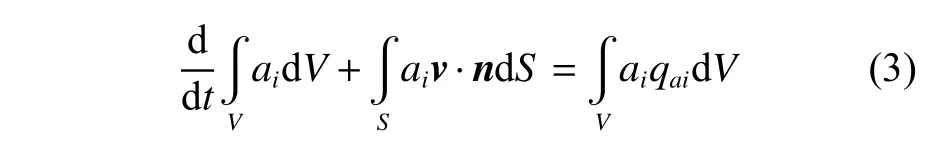
式中，qai為體積分數ai的一個體積源。

1.4 造 波

造波方法采用邊界輸入法。定義縱向坐標x對應于波浪傳播方向，垂向坐標z為鉛垂向上的方向。根據五階Stokes波的解析解，在計算域的邊界分別設定水質點x方向（波傳播方向）速度ux，z方向速度uz和波面瞬時高度η，如下所示。

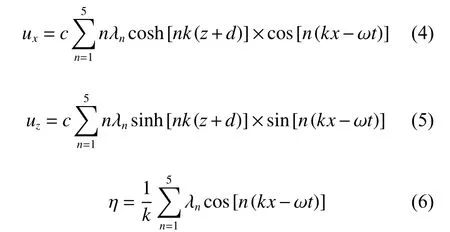
式中：ω為圓頻率；c=coshkd，其中，d為水深，k為波數；n為Stokes波階數。其他符號含義見文獻[5]。

1.5 消 波

在對波浪傳播進行數值模擬時，因計算域范圍有限，在各邊界處常會發生波浪反射的情況，影響造波精度，因此，在研究時使用了阻尼消波法消除邊界處的反射波，以使模擬計算環境更接近于真實情況。該方法在動量守恒方程 (2) 中將動量源項qi定義如下：

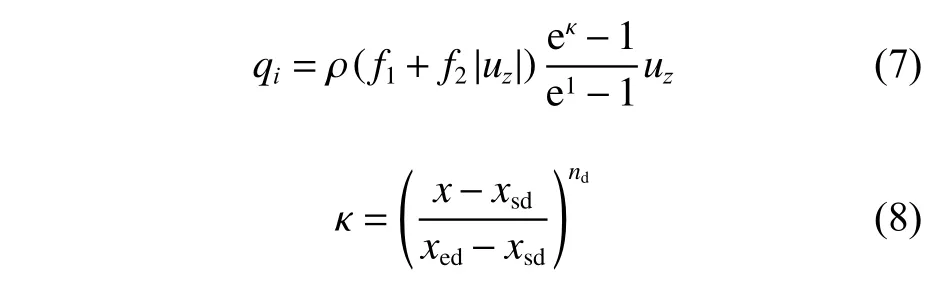
式中：fl為線性阻尼系數；f2為二次阻尼系數;uz為垂向坐標z方向的速度分量；eκ?1/e1?1為彎曲項，其中κ為彎曲指數；xsd和xed分別為阻尼層開始和結束時的x坐標（波傳播方向），一般xed位于計算域末端，故阻尼消波區的長度為xd=|xed?xsd|；nd控制阻尼消波區的波形衰減形狀，一般取nd=2。

為實現理想的消波效果，xd,fl和f2需根據波浪參數進行精確調整[6]。推薦只使用線性消波項（f2=0），阻尼消波區的長度設為2倍波長（xd=2λ），線性阻尼常數f1=Ψ1ω，其中系數Ψ1=π。

1.6 離散格式及其他設置

本文使用有限體積法（finite volume method,FVM）將控制方程離散化。所有數值差分、微分和積分都是基于二階近似。每個代數方程包含來自網格中心及所有相鄰網格中心的未知值，獲得的耦合方程組被線性化，并由隱式非定常求解器求解。計算時，使用SIMPLE方法獲取壓力值并校正速度。壓力的松弛因子為0.4，其他所有變量的松弛因子均為0.9。使用高分辨率接觸面捕捉（high-resolution interface capturing，HRIC）方法提高自由液面的捕捉精度。同時，激活梯度平滑，減少在大網格長高比下的波面振蕩。

2 誤差分析

數值模擬的誤差來源主要有：模型誤差，即數學模型理論解與物理情況實際值間的誤差；離散誤差，即離散方程的解與數學模型理論解間的誤差；迭代誤差，即迭代算法的解與離散方程解間的誤差。

本研究只考慮實際的數值造波結果與理論解間的差異，故無需考慮模型誤差。而通過對線性方程組的求解和利用SIMPLE法進行足夠次數的迭代，迭代誤差可遠遠小于離散誤差[7]，因而，離散誤差是主要誤差來源。為便于討論，本文參考一維波動方程來分析影響離散誤差的具體參數。波面控制方程為：

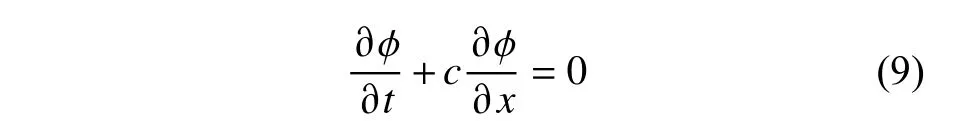
若以顯式一階迎風格式對波面方程(9)進行有限差分，離散誤差則為式(10)等號右端項之和。

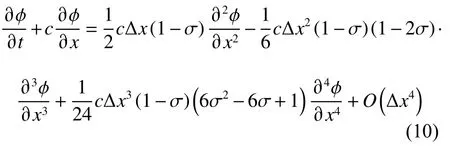
式中：φ為速度勢；c為波速；σ為庫朗數（Courant–Friedrichs–Lewy number），σ=cΔt/Δx，其中，Δx為網格尺寸，Δt為時間步長。由式(10)可知，波浪傳播的離散誤差主要由2個無量綱數影響：

1） 庫朗數σ，即單個時間步內波浪傳播的網格數。

2）與波浪尺度相比的幾何分辨率Δx/λ（其中λ為波長）。當Δx越小，幾何分辨率越高，單個網格內的梯度就會越小，離散誤差也越小[8]。

離散誤差的具體形式會因具體方程及所用的離散格式而不同，但無論哪種形式，誤差的大小都與庫朗數和幾何分辨率有關。對于二維造波問題來說，庫朗數定義為：

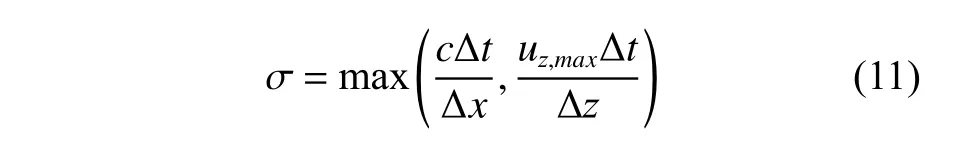
式中，uz,max為z方向的速度最大值。幾何分辨率則與長度 方 向x和高度 方 向z的 尺度比Δx/λ和Δz/H有關（其中H為波高，λ 為波長）。為控制網格幾何分辨率的大小，若定義波面附近加密區z方向的網格數為Nz，網格長高比為r，則有Δz=H/Nz，Δx=rΔz=rH/Nz。

當網格尺寸Δz和Δx確定后，可通過改變時間步長Δt來確定庫朗數大小，具體如式（12）所示。

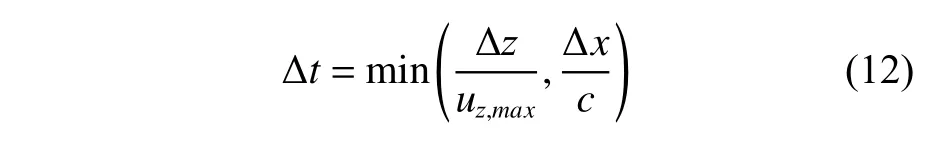
綜上，后續研究將圍繞最小加密區z方向的網格數Nz、網格長高比r以及庫朗數σ這些參數展開。造波誤差則由波幅誤差em和相位偏差ep來衡量[9]。定義波幅的理論解為E=|E|ejθ，數值解為E′=|E′|ejθ（其中θ 為極坐標系旋轉角，θ?為其估計值），則坐標點(xN，zN)(N表示數據點)的波幅百分比誤差em和相位偏差ep(單位：rad)為：

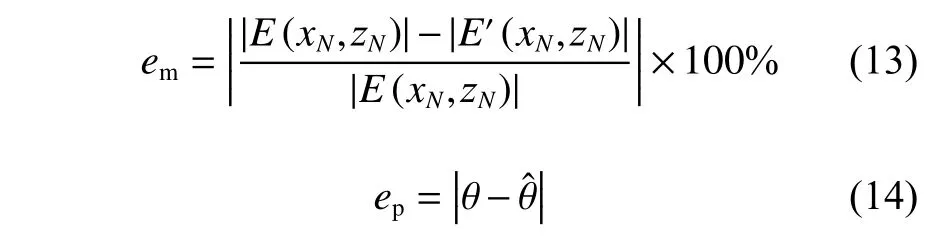
在后處理分析誤差時，分別對各位置波幅誤差em在波周期 (0～10)T，(10～20)T，(20～30)T和(30～40)T之間的時刻進行時間平均，相位偏差ep則主要關注每個位置在t=10，20，30，40T時刻的相位偏差ep。

3 算例設置

3.1 計算域設置

計算模擬二維深水波情況，計算域尺寸根據所對應的波浪波長λ進行調整，計算域如圖1所示。為研究波浪在空間上傳播可能存在的衰減，計算域長度Lx=10λ。為模擬深水條件，消除上、下邊界對流場的影響，計算域高度Lz=6λ，其中水深d=4λ，其他為空氣相。坐標原點設在計算域入口邊界靜水液面高度處，縱向坐標x對應于波浪傳播方向，垂向坐標z對應于鉛垂向上的方向。

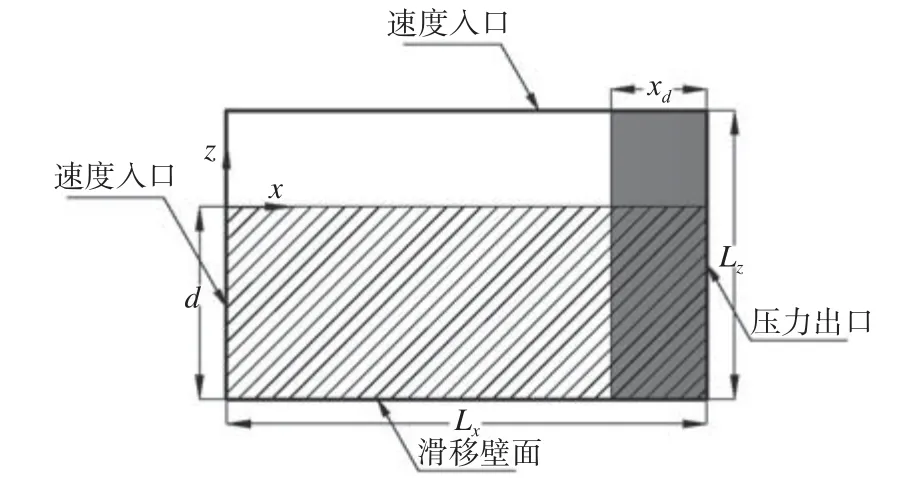
圖1 計算域設置示意圖Fig.1 Schematic view of computational domain setting

入口邊界（x=0）設為速度入口，數值波采用五階Stokes波形式；出口邊界（x=Lx）設為壓力出口，并向前設置xd=2λ長度的消波區；底部邊界（z=?4λ）設為滑移壁面，對應底部不可穿透條件；頂部邊界（z=2λ）設為速度入口，對應于開放的頂部條件。

3.2 網格設置

為了能夠精確地捕捉數值波的交界面，需對波面附近網格進行局部加密。這里，選擇波高方向網格數Nz和網格長高比r=Δx/Δz作為網格設計策略的參數。如圖2所示，在自由液面附近沿波浪傳播方向共設置5個網格加密區。

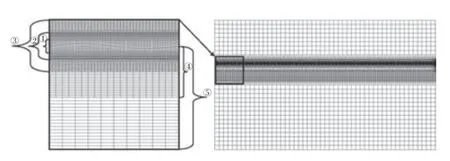
圖2 網格加密區示意圖Fig.2 Schematic view of the zones by grid refinement

1) 加密區①，高度h1=1.25H，使加密區覆蓋整個波高范圍。加密區內使用各向異性網格尺寸，高度方向的網格尺寸Δz=1/Nz；長度方向的網格尺寸Δx取Δz的r倍。Nz和r的取值將在下文說明。

2) 加密區②和③的高度h2,h3分別為2.5H和5H，網格尺寸分別為加密區①的2和4倍，并保持長高比r不變，以實現網格尺寸的平滑過渡。

根據線性波的理論解，波面以下z=?0.5λ處質點運動速度小于波面處的5%，z=?λ處質點運動速度小于波面處的0.5%。因此，加密區④和⑤的高度h4，h5分別為0.5λ和λ，同樣保持網格長高比r不變，網格尺寸分別為加密區①的8倍和16倍。

3.3 波高監測設置

所有算例模擬計算了各波形從物理時間t=0到t=40T的傳播過程。為監測波幅及周期在時間和空間上的變化，在x=1,2,···,8λ的位置設置了8個探針。對于x>8λ的區域，因屬于消波區，故不再進行監測。

4 各參數對造波精度的影響

根據上述分析，針對可能影響造波精度的各重要參數進行了研究，參數包括：影響迭代誤差的內迭代次數n以及影響離散誤差的幾何分辨率和庫朗數σ。其中，幾何分辨率由加密區①波高方向的網格數Nz和網格長高比r來控制，庫朗數σ則通過改變時間步長來控制。誤差主要關注x=8λ位置的探針在t=40T時刻的波幅誤差em和相位偏差ep，即每組算例中em和ep的最大值。作為對照算例A0，其參數設置如表1所示，其他算例則在A0算例的基礎上修改相關參數得到。

表1 對照算例A0的參數設置Table 1 Parameter setting of Case A0 for comparison

4.1 內迭代次數

為研究內迭代次數n對迭代誤差的影響，在對照算例A0的基礎上修改了4個不同的內迭代次數。分別設為5,8,10和20次，對應算例編號為B1～B4，如表2所示。表中，加黑數字表示本組算例中的變量參數（以下同）。誤差計算結果如圖3所示。

表2 B1～B4算例參數設置Table 2 Parameter setting for Case B1-B4

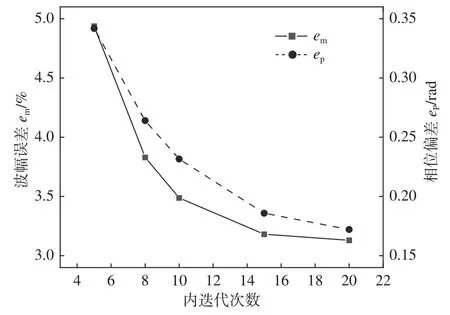
圖3 不同內迭代次數對應的誤差變化Fig.3 Error variation corresponding to different inner iteration times

由圖3計算結果可知，波幅誤差em和相位偏差ep隨內迭代次數n的增加而降低；當內迭代次數達到15次以上時，波幅誤差em降至3.18%，相位偏差ep降至0.17 rad，這兩個誤差已達到較低水平，且隨著內迭代步數的繼續增大，并無明顯改善，因此，選擇15次作為以下算例的內迭代次數。

4.2 庫朗數

在對照算例A0的基礎上修改庫朗數取值，并研究其對造波精度的影響。設置從0.2～0.5的4個不同庫朗數取值，算例編號對應C1～C4，如表3所示。誤差計算結果如圖4所示。

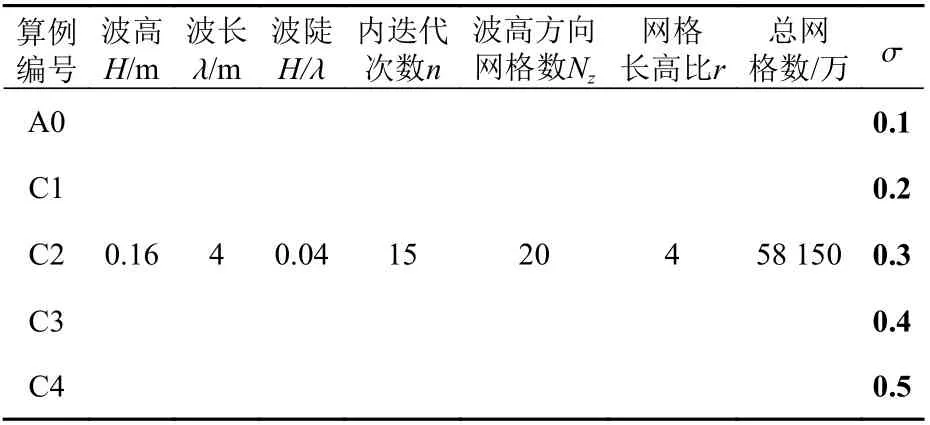
表3 C1～C4算例參數設置Table 3 Parameter setting for Case C1-C4

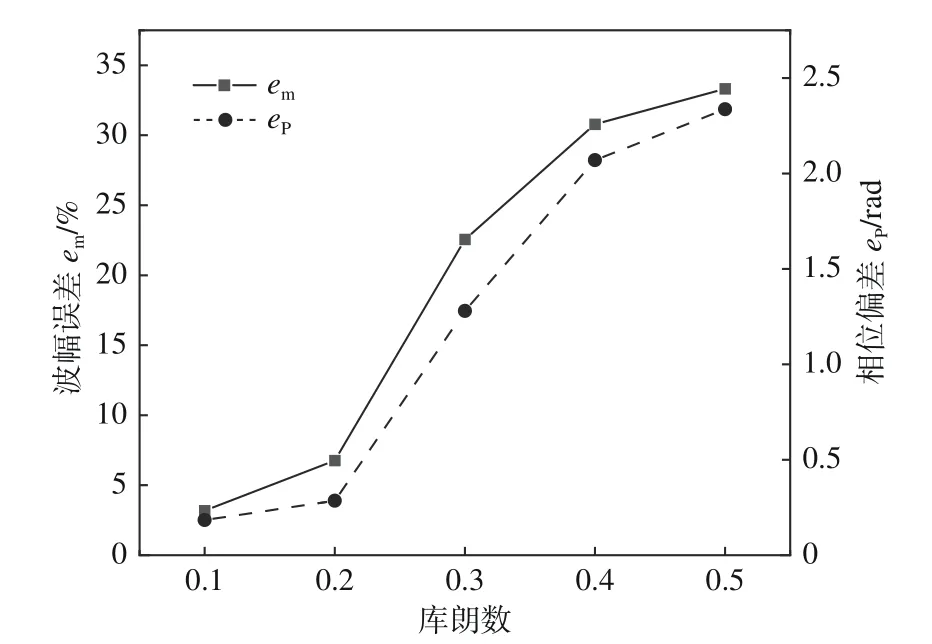
圖4 不同庫朗數對應的誤差變化Fig.4 Error variation corresponding to different Courant numbers

由圖4計算結果可知，波幅誤差em和相位偏差ep都隨庫朗數的增加而急劇增大。在庫朗數為0.5時，數值波波幅與理論值相比衰減了33%，相位偏差可達2.31 rad，對離散誤差有極大影響。當波面處的庫朗數為0.1時，波幅誤差em可控制在5%以內，相位偏差ep約為0.2 rad。繼續調低庫朗數雖可以進一步降低誤差，但卻會使時間步過小，計算成本將成倍增加。鑒此，綜合考慮計算精度和成本后，本文使用0.1作為后續算例的庫朗數較為合理。

4.3 波高方向網格數

波高方向網格數Nz影響沿波高方向網格的幾何分辨率，進而對離散誤差造成影響。設置4個不同的Nz值算例進行誤差影響的驗證。具體參數設置和誤差結果見表4和圖5。

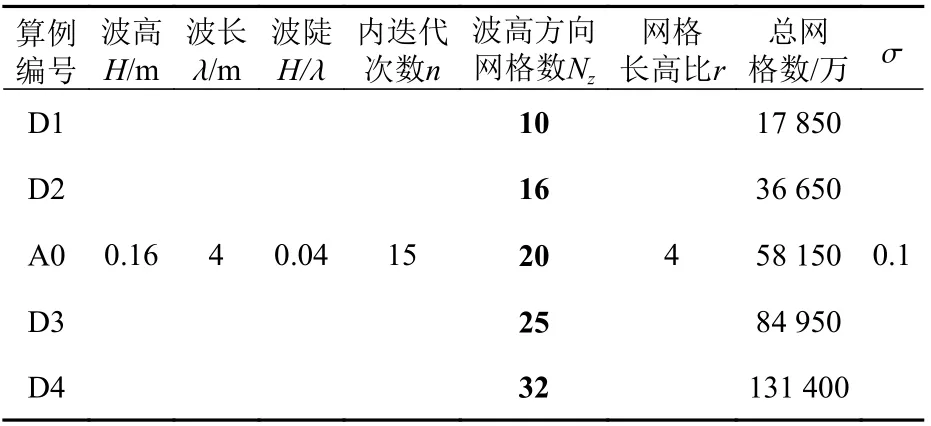
表4 波高方向網格數影響算例參數設置Table 4 Parameter setting of cases with different mesh number in the wave height

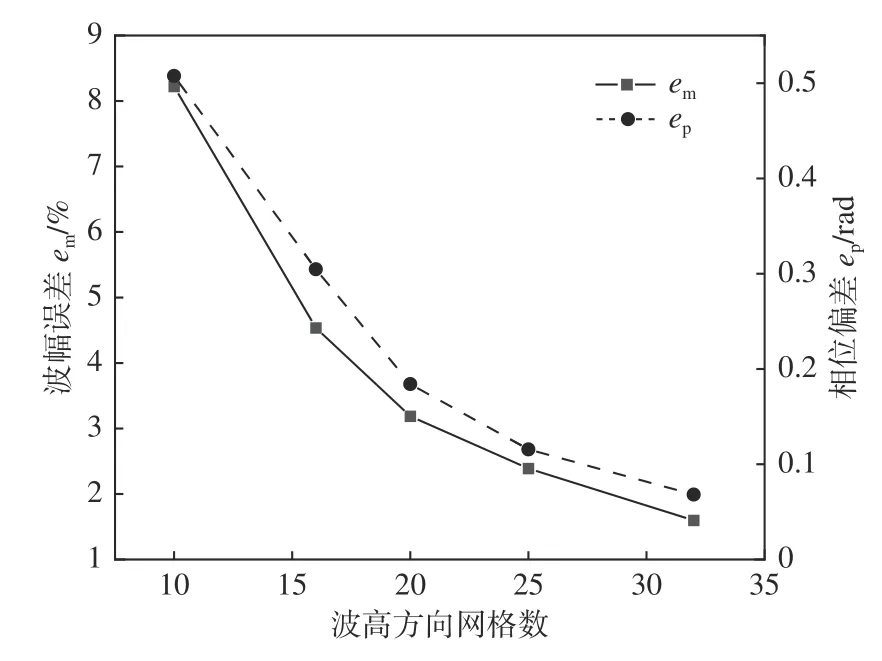
圖5 波高方向網格數對應的誤差變化Fig.5 Error variation corresponding to the mesh number in the wave height direction

由表4和圖5所示計算結果可知，隨著波高方向網格數Nz的增加，波幅誤差em和相位偏差ep都呈明顯的下降趨勢。當Nz為20時，波幅誤差em降至3.5%以下，相位偏差ep降至0.2 rad以下，造波精度在可以接受的范圍內。算例D3和D4相較于A0，雖然兩種誤差都有一定的降低，但過大的網格數會造成計算成本的急劇增大。鑒此，綜合考慮計算精度及計算成本，后續計算選擇20作為波高方向的網格數值。

4.4 網格長高比

波高方向網格數Nz確定后，網格長高比r決定了波傳播方向的網格分辨率，這是影響離散誤差的另一個重要因素。在試算中發現，網格長高比r對誤差的影響在不同波陡下有很大差異。為研究其具體影響，在保持波長不變的前提下，進行了0.01～0.07共7組不同波陡下的數值計算，每組波陡下完成3～4個不同長高比網格的算例，共計26個。各算例的具體參數設置和誤差結果如表5和圖6所示。

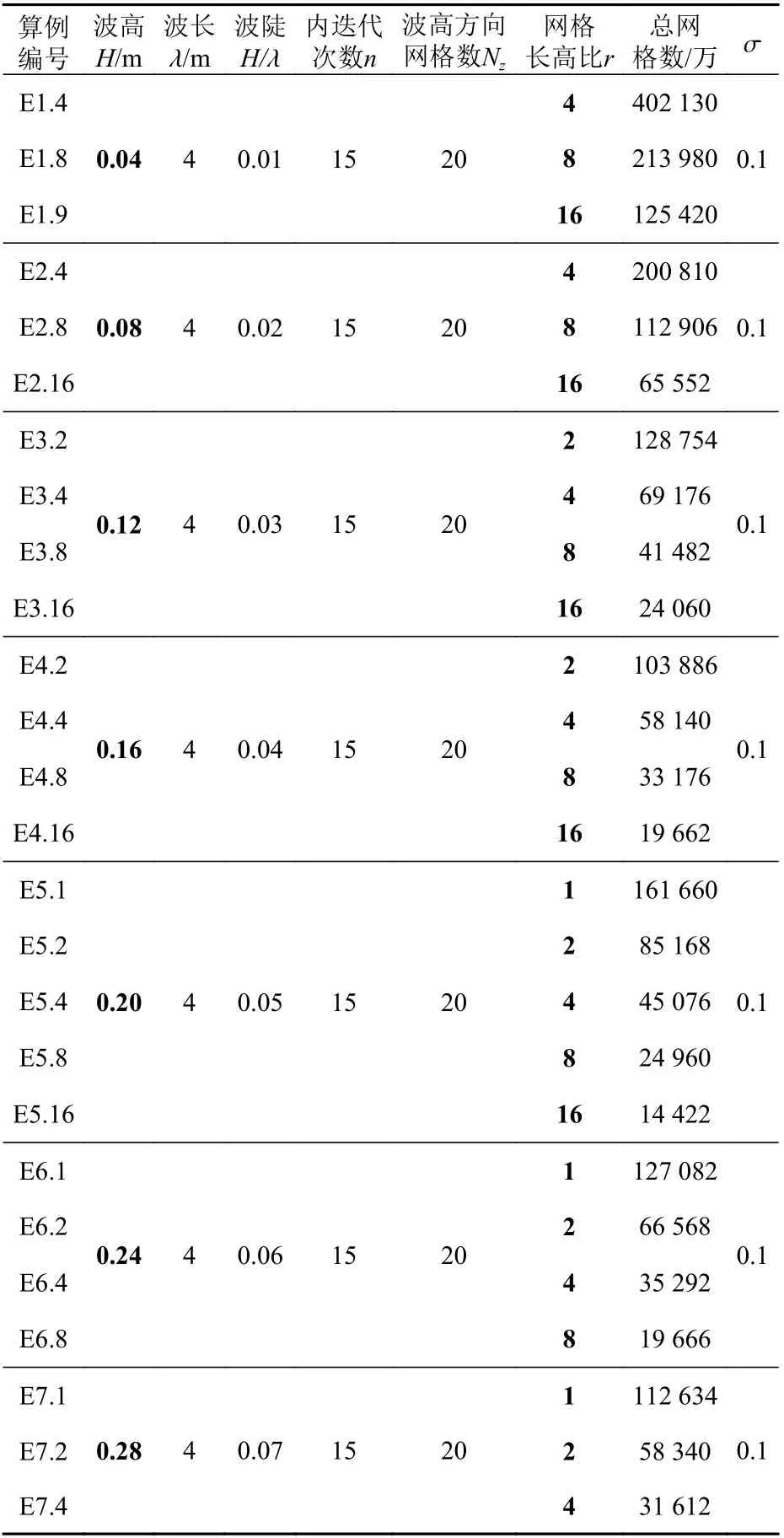
表5 不同網格長高比算例參數設置Table 5 Parameter setting for cases with different mesh aspect ratios

波幅誤差em和相位偏差ep的對比分別在t=20T和t=40T這2個時刻及x=8λ位置處展開。由誤差結果分析可知，隨著網格長高比r的增加，網格分辨率的降低使得em和ep都逐漸增大，且變化趨勢基本相同；不同波陡的波浪對于網格長高比r的敏感性不同，波陡較小的算例（例如，E1和E2兩組）在使用較大的r來劃分網格時仍能保持較低的誤差，而對于大波陡的算例（例如，E6和E7兩組），則需要非常小的r才能滿足誤差要求。鑒此，綜合考慮計算精度及計算成本，對于波陡在0.01～0.06之間的波浪，本文通過對圖6及圖7所示的結果進行擬合可得到網格長高比，具體由下式計算：

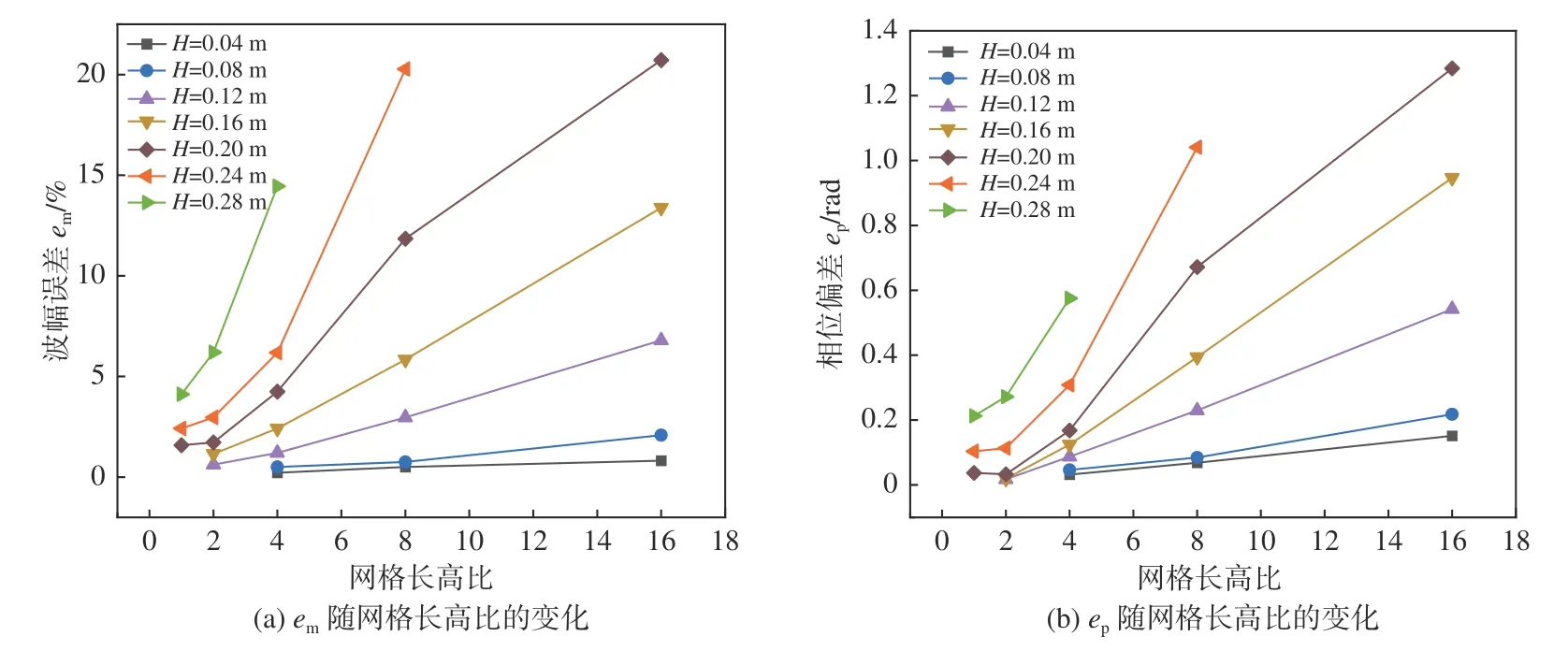
圖6 em與ep隨網格長高比的變化（t=20T，x=8λ）Fig.6 Variation of em and ep with grid aspect ratio at t=20T and x=8λ

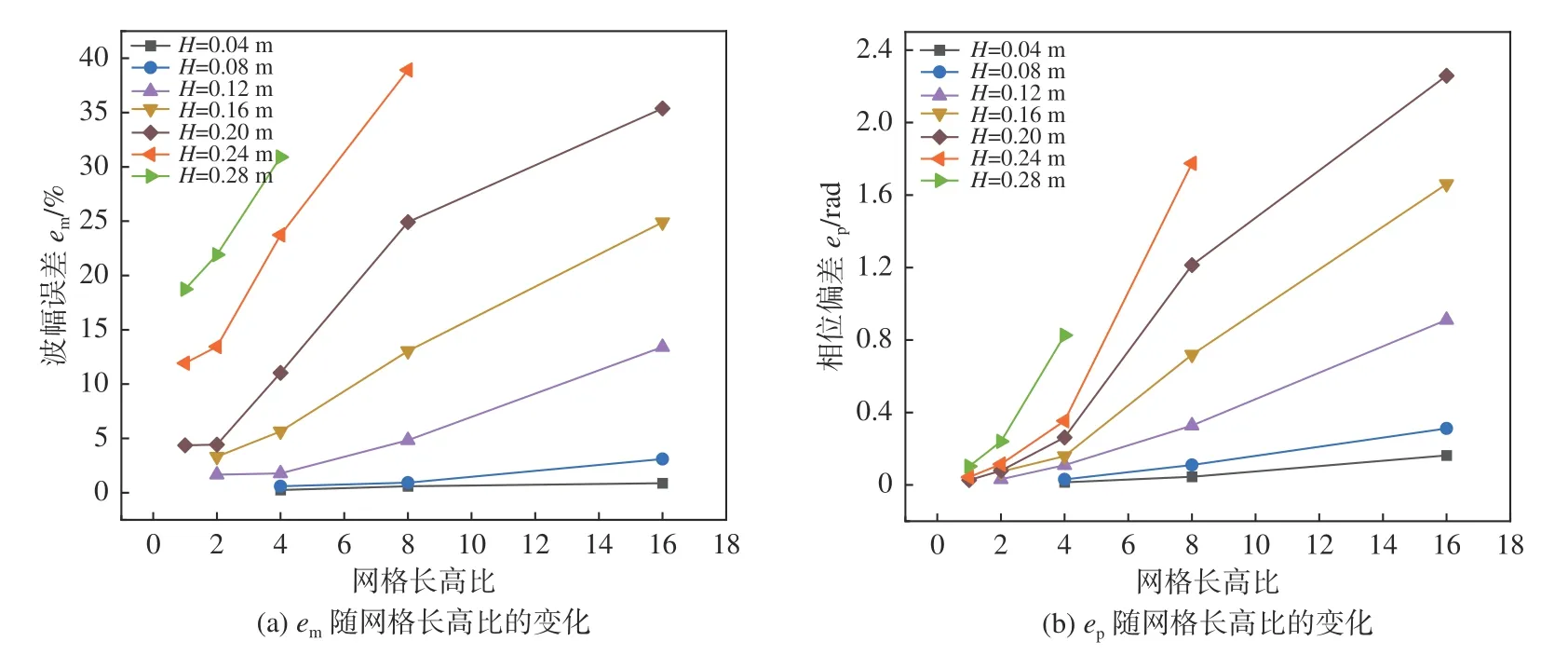
圖7 em與ep隨網格長高比的變化（t= 40T，x=8λ）Fig.7 Variation of em and ep with grid aspect ratio at t= 40T and x=8λ

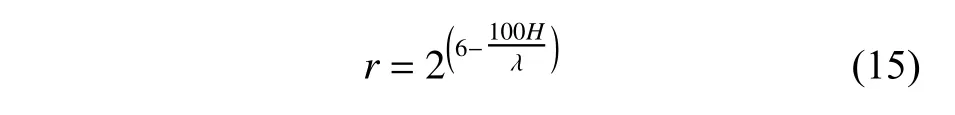
根據式（15）計算的r可以滿足：t=20T時刻的波幅誤差em約5%，相位偏差ep約0.2 rad；t=40T時刻波幅誤差em約10%, 相位偏差ep約0.4 rad。

而對于波陡H/λ≥0.06的波浪而言，即使使用網格長高比為1的網格進行計算，仍然不能滿足上述誤差要求。對于此類大波陡波浪，可能需要改進自由液面捕捉方法或者使用其他創新方法等才能夠得到較為理想的結果。

4.5 參數設置的總結

經過上述數值計算及結果對比可知，為實現多周期穩定數值造波，推薦采用以下設置：

1） 選用標準低雷諾數K-Epsilon湍流模型，湍動能和湍流耗散率的初始值分別為1×10?5J/kg和1×10?4m2/s3，以降低湍流黏度對波面衰減的影響；

2） 在計算域下游邊界設置阻尼消波區，阻尼消波區的長度設為兩倍波長（xd=2λ）；僅使用線性消波項（f2=0），線性阻尼常數f1=Ψ1ω；

3） 使用HRIC方法，并激活梯度平滑選項；

4） 內迭代次數設為15次或以上，自由液面處最大庫朗數維持在0.1以下，并據此調整時間步長；

5） 對自由液面附近進行網格加密，加密區①波高方向的網格數Nz設為20，網格長高比r使用式(15)計算，其他加密區網格尺寸參考4.3節。

計算結果表明，使用上述參數設置方法，可以實現多周期的穩定數值造波，波幅誤差em和相位偏差ep滿足工程應用的精度要求。圖8所示為算例E4.4在x=8λ位置波高隨時間的變化曲線，圖9所示為t=40T時刻波高隨空間位置的變化曲線，其中波高、時刻和位置都進行了無量綱化處理。由圖8和圖9可以看出，實際波幅線（黑色）與理論波幅線（紅色）基本重疊，實際波幅與理論波幅在時間上吻合較好，空間上波形分布均勻，但隨著傳播距離的增加存在一定的衰減，可見，消波區的波形消波效果良好。

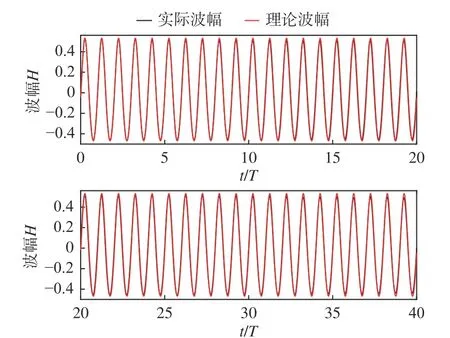
圖8 算例E4.4在x=8λ位置波高隨時間變化Fig.8 Variation of wave height with time at x=8λ in Case E4.4

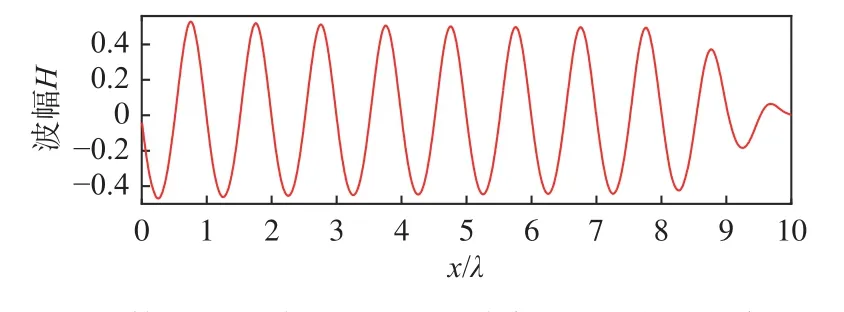
圖9 算例E4.4在t=40T時刻波高隨空間位置的變化Fig.9 Variation of wave height with spatial position at t=40T in Case E4.4

5 數值造波方法應用

以上算例都是針對模型尺度下的二維數值造波研究，為驗證本文所提參數設計方法在三維數值造波問題上的適用性，計算了KCS船型在迎浪中的阻力和運動響應，并與工程流體動力學（EFD）試驗值[10]進行對比。

為與實驗條件保持一致，波長設為λ=0.5LBP=115 m，波陡H/λ=1/60，弗勞德數Fr=0.26。由于船體左右對稱，為減少計算量，僅對半船的流場進行模擬，并使用重疊網格方法及DFBI (displaying dynamic fluid body interaction)模型實現船體迎浪時的升沉與縱傾運動。

背景區域及重疊域網格采用切割體非結構網格形式，其中，背景區域網格基準尺寸取為4.0H，重疊區域網格基準尺寸取為0.2H，并在背景區域設置多層嵌套的加密區以保證體網格尺寸的過渡平滑；船體邊界層采用棱柱層網格來捕捉，邊界層共劃分有16層，增長率為1.2。自由液面處則根據4.3節所述參數進行加密，y軸方向網格大小取為4.0H。最終，得到的背景區域體網格總數為430萬，重疊區域體網格總數為1 100萬，圖10所示為中縱剖面船體附近的網格示意圖。

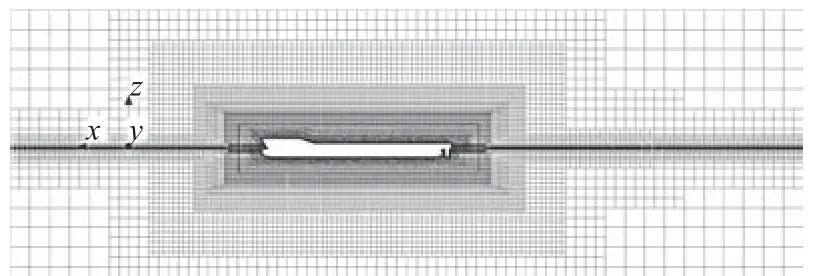
圖10 船體附近網格Fig.10 Grids near the hull

總共計算20個波周期，在中縱剖面船體前方一倍LBP處設置探針，監測得到的波高變化曲線如圖11所示，由圖11可知，在整個計算時間內來波的波幅都無明顯衰減。計算結果主要關注波浪增阻系數σaw、升沉和縱傾的傳遞函數（transfer function，TF），其計算公式分別如下：

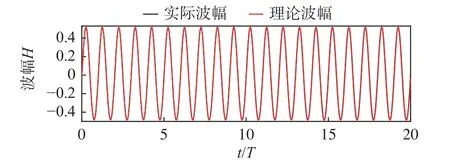
圖11 船前一倍LBP處波高的變化Fig.11 Variation of wave height at a distance of onefold-LBP ahead the ship

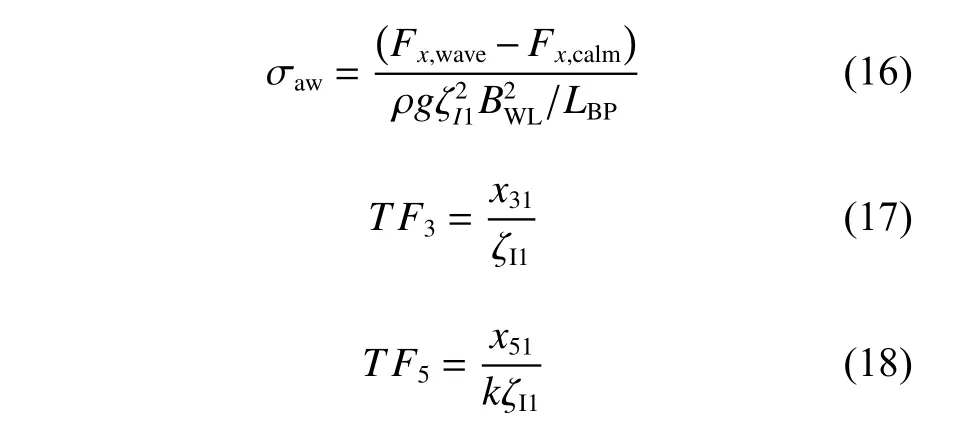
式中：Fx,wave和Fx,calm為船體在波浪和靜水中的縱向受力的平均值；BWL為水線面寬度；LBP為垂線間長；x31，x51和ζI1分別為升沉、縱搖和波高瞬時幅值的一階傅里葉系數；波數k=2π/λ。其中，升沉和縱搖以船體重心為參考點。

圖12所示為自由液面在初始和計算一段時間后的自由液面波形對比圖，由自由液面波高圖可清晰地捕捉到開爾文船行波。增阻系數、升沉和縱傾的傳遞函數的計算結果見表6。

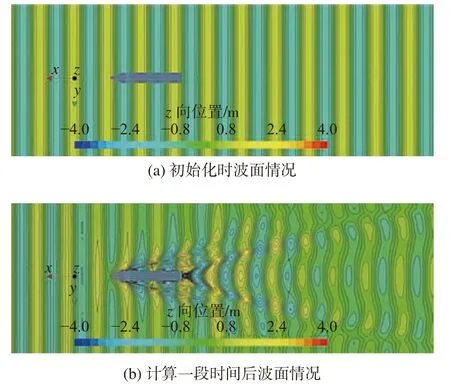
圖12 自由液面波形對比Fig.12 Comparison of wave pattern for free surface

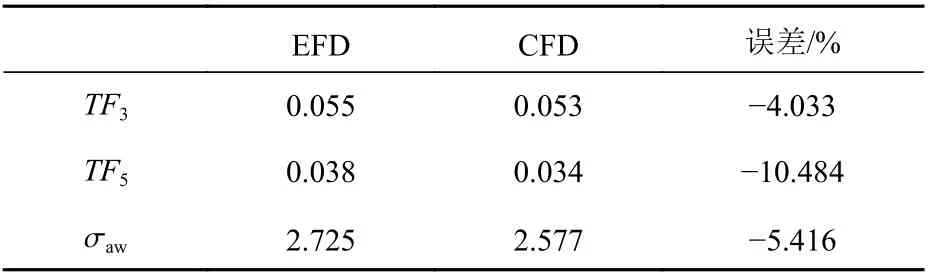
表6 CFD與EFD計算結果對比Table 6 Comparison of calculation results by CFD and EFD

由表6的的計算結果可知，CFD計算結果與EFD結果相比均偏低，誤差約為4%～10%，這進一步驗證了本文所提造波參數設計方法可以推廣到三維數值造波的相關問題之中。

6 結 論

本文分析了一維波動方程的離散形式，得到了影響數值造波精度的幾個關鍵參數及其對造波效果的具體影響。通過設置不同參數對深水二維水池進行了波浪模擬，對每組算例的計算誤差進行評估，綜合考慮計算精度和成本，確定了各參數的最佳值。而且，提出了包括湍流模型、消波方法、內迭代次數、庫朗數及網格設置的一整套參數設計方法。通過分析計算，得到如下結論：

1） 數值造波誤差主要包括離散誤差和迭代誤差。離散誤差是影響數值造波精度的主要誤差因素，與之相比的迭代誤差可通過增加內迭代次數來降低到遠小于離散誤差的范圍；

2） 影響離散誤差大小的主要因素為庫朗數和網格分辨率。其中，庫朗數對誤差影響較大，需確保自由液面庫朗數在0.1以下，網格分辨率則需通過調整波高方向網格數及網格長高比來實現；

3） 波陡H/λ對數值造波的結果影響很大。在H/λ≤0.06的波陡范圍內，使用4.5節參數設計方法可使得20個波周期和40個波周期內波幅誤差分別約為5%和10%，相位偏差分別約為0.2和0.4 rad，并可推廣到三維造波問題中；

4） 對于五階Stokes波以外的其他規則的非線性波或線性波，計算結果表明，上述參數設計方法均可一定程度上減少造波誤差，使造波結果滿足精度要求；

5） 對于波陡H/λ≥0.06的大波陡波浪，即使使用網格長高比r=1的網格計算仍有較大誤差，若為提高計算精度而進一步增加網格分辨率，則計算成本將變得過高，不具有實際應用的可行性。對于此類大波陡數值造波問題，仍需通過進一步研究和創新方法來解決。