內河多工況船機槳匹配優化設計

孫林，陳輝*，管聰

1 武漢理工大學 能源與動力工程學院，湖北 武漢 430063

2 武漢理工大學 高性能艦船技術教育部重點實驗室，湖北 武漢 430063

0 引 言

隨著內河航運業的快速發展，以及船舶噸位和功率的不斷增加，對內河船舶的船?機?槳匹配問題提出了更高要求。傳統的內河船舶推進系統設計是依據逆水上行時的工況進行船?機?槳的匹配設計而得到各個參數，該方法只能保證柴油機在逆水上行時工作在設計工況點，而在順水下行時會出現柴油機負荷率和螺旋槳效率低及燃油消耗高等問題，從而導致航行成本過高。因此，在充分考慮內河航行工況的基礎上對船舶推進系統進行設計，對降低內河船舶航行成本和提高推進系統效率具有重要意義。

目前，在船?機?槳匹配設計領域，已開展了一系列研究。Esmailian等[1]在考慮全壽期燃油消耗（LFC）和成本這2個目標函數的基礎上，基于NSGA-Ⅱ算法對螺旋槳幾何參數、船體參數及螺旋槳葉片應力進行了優化，給出了采用B系列螺旋槳的計算結果，結果顯示采用該方法能使2個目標函數顯著最小化。覃峰等[2]將遺傳算法引入機?槳匹配優化設計中，建立了以推進系統總效率為目標函數的優化模型，針對傳統的船?機?槳匹配方法，較好地改善了計算規模和優化結果。Ren等[3]研究并論證了能效設計指標（energy efficiency design index，EEDI）對船?機?槳匹配設計的影響，其通過改變系統匹配參數，如航速、有效功率和螺旋槳直徑，觀察了EEDI的變化趨勢與程度，開發了供船舶推進系統匹配設計和EEDI計算的程序，為EEDI規則下的船舶、主機和螺旋槳設計提供了參考。馬永杰[4]針對船舶的實際運行情況，建立了基于動力推進系統船?機?槳匹配的實時動態數學模型，并在船?機?槳匹配實時動態模型的基礎上編寫了船?機?槳匹配仿真軟件，通過該軟件，可以模擬船舶的啟動、加速、減速、倒車等多種工況。

在船?機?槳匹配設計領域，目前的研究主要是依據傳統的機?槳匹配方法進行設計，還沒有專門針對內河船舶的設計方法。為此，本文將以航行于武漢—上海的7 500 t散貨船和B系列五葉螺旋槳為例對其推進系統進行設計和分析。首先，分析長江中下游的通航環境，使用傳統的方法對不同工況下內河船舶的各參數進行設計，比較得到各參數對整體推進系統的影響；然后，對內河船舶的船?機?槳匹配過程進行建模；最后，以航行成本和推進系統效率為目標函數，以螺旋槳的各設計參數、主機功率等為變量，應用NSGA-Ⅱ算法進行多目標優化，得到滿足要求的船舶推進系統設計參數。

1 船?機?槳匹配

1.1 船?機?槳匹配設計參數

船舶在航行過程中，船體、主機和螺旋槳一起組成一個統一的整體。主機燃燒燃料產生的能量通過軸系傳遞給螺旋槳，螺旋槳產生推力確保船舶可以按照設定的航速運行，這三者之間相互匹配，以確保船舶推進系統能量傳遞的平衡和穩定變化。在船舶推進系統中，船體、主機和螺旋槳各設計參數之間的關系如圖1所示。圖中：Vs為船舶航速；R為船舶阻力；PE為有效功率；t為推力減額系數；D為螺旋槳直徑；T為螺旋槳有效推力；ρ為水的密度；n為螺旋槳轉速；P/D為螺旋槳螺距比；w為伴流系數；VA為螺旋槳進速；J為進速系數；PB為軸功率；PD為螺旋槳收到的功率；ηR為相對旋轉效率；Q為螺旋槳的扭矩；KT為推力系數，KQ為扭矩系數，KT=f(J，P/D)，KQ=f(J，P/D)，其中f表示KT，KQ是關于J，P/D的函數式；η0為敞水效率。

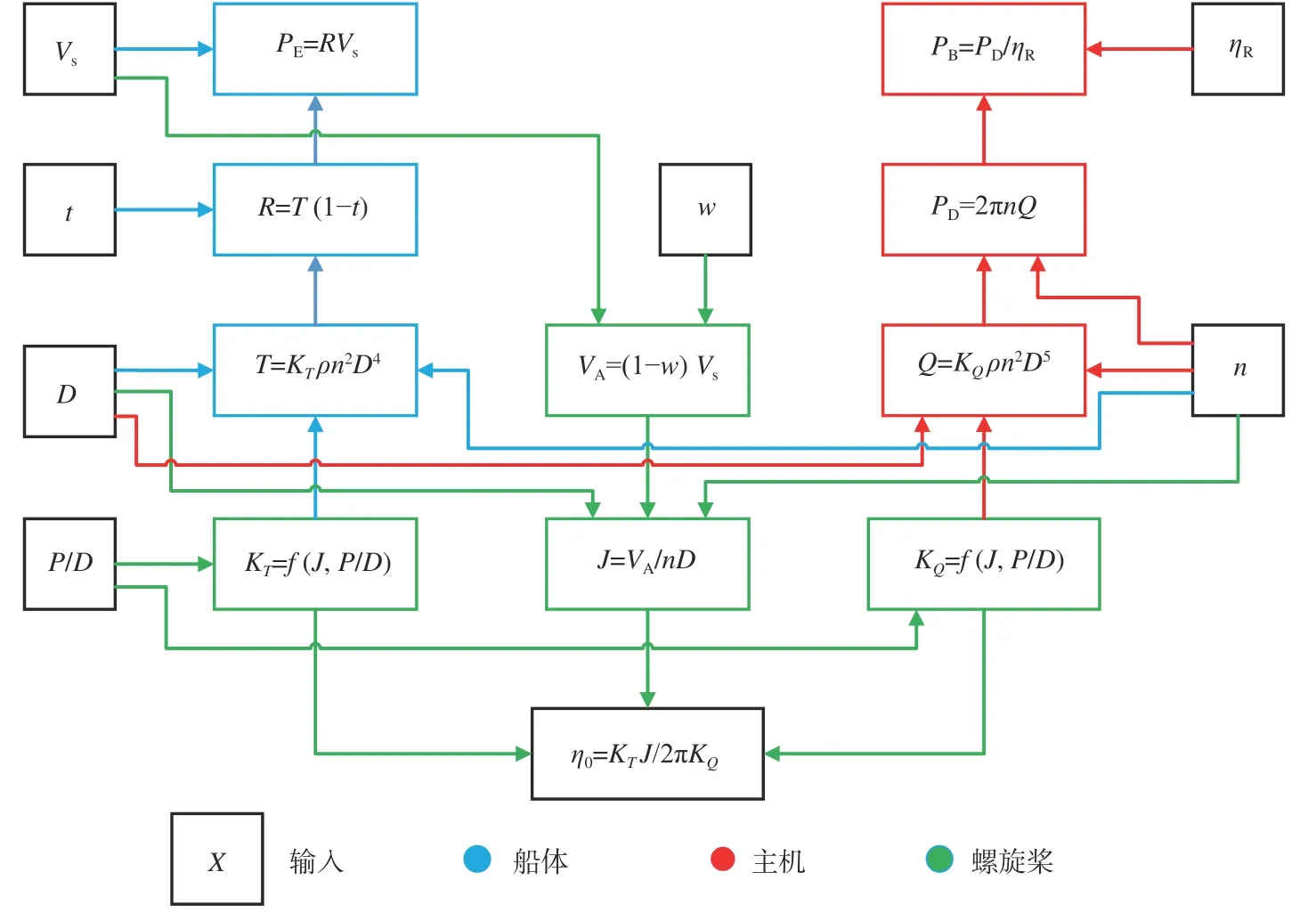
圖1 船?機?槳匹配框圖Fig.1 Framework of ship-engine-propeller matching

1.2 傳統的船?機?槳匹配方法

傳統的船?機?槳匹配分為船舶?主機匹配與主機?螺旋槳匹配2個階段[5-8]。

1） 已知設計航速和有效功率曲線（圖2），依據初步擬定的螺旋槳直徑D，計算得出螺旋槳的最佳轉速n、敞水效率η0、螺距比P/D和主機功率Ps

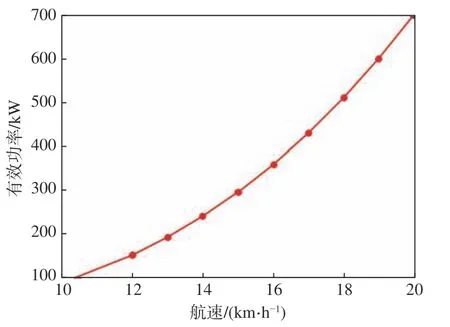
圖2 有效功率曲線圖Fig.2 Curve of effective power

2） 由在第1階段計算得到的螺旋槳所需主機輸出功率，根據柴油機的減額輸出特性、船舶實際運行工況以及經濟性等，基于第1階段所求的螺旋槳設計工況點（圖3，圖中KT_ship為船舶推力系數，曲線KT_ship與KT的交點即為螺旋槳設計工況點）確定主機的設計工況點，即主機的額定功率以及額定轉速。

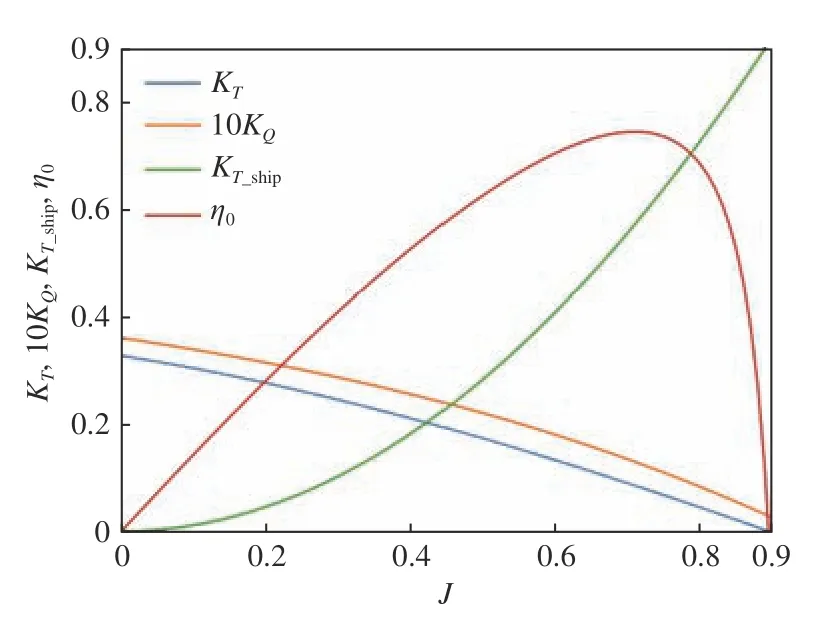
圖3 螺旋槳敞水特性曲線示意圖Fig.3 Curves of the propeller open water efficiency

經過船舶?主機匹配得到主機額定功率和轉速之后，需要進行主機?螺旋槳匹配設計，即設計一個能與主機良好配合工作的螺旋槳，以使螺旋槳的效率達到最高，同時保證船舶達到設計航速的要求。具體流程為：已知主機功率Ps、轉速n及船舶有效功率曲線，確定該主機所匹配的螺旋槳直徑D，螺距比P/D以及所能達到的最大航速Vmax。

2 內河工況對船舶推進系統設計的影響

2.1 內河工況分析

長江航道的主要航線是宜賓—上海。其中，宜賓—宜昌為上游，宜昌—武漢為中游，武漢—上海為下游。圖4所示為長江航道圖。

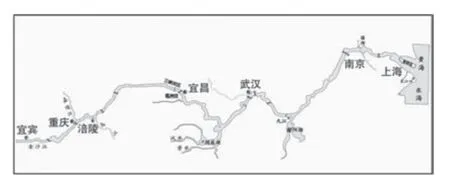
圖4 長江航道圖Fig.4 Inland waterway chart of Yangtze river

長江航道各區域的水流速度如表1所示。

表1 長江航道水流速度及里程Table 1 Water flow rate and range of Yangtze waterway

2.2 影響因素

本文以航行于武漢—上海的7 500 t散貨船和B系列五葉螺旋槳為例進行分析。分別在0，1，2，3，4，5 km/h的水流速度和調整螺旋槳設計直徑的情況下，使用傳統方法對其進行船?機?槳匹配設計，得到主機額定功率、螺旋槳設計直徑和水流速度V水（工況）三者間的關系，以及得到敞水效率、螺旋槳設計直徑和水流速度V水（工況）三者間的關系，分別如圖5和圖6所示。

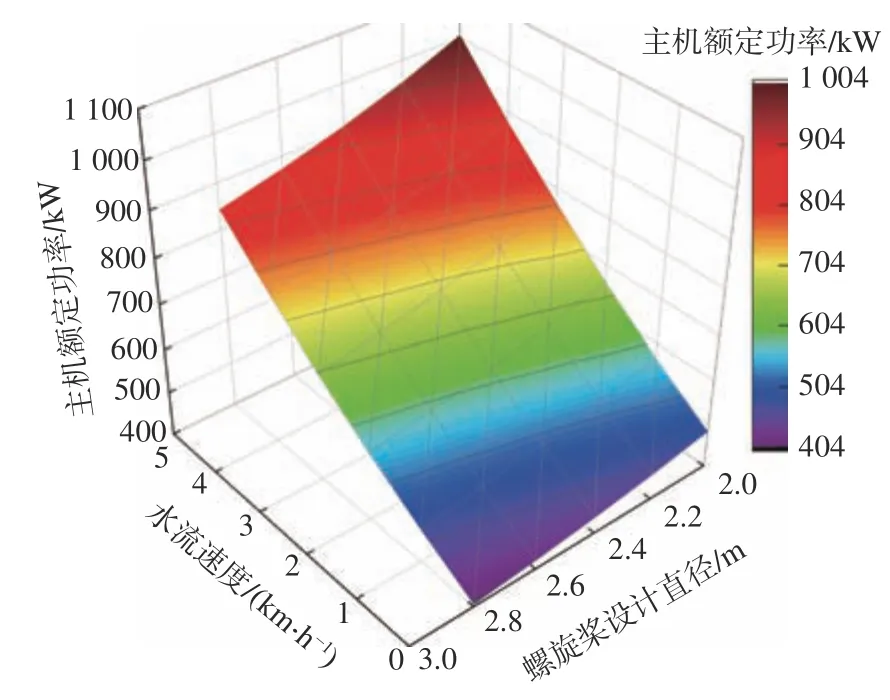
圖5 主機額定功率、螺旋槳設計直徑和水流速度三者間關系Fig.5 Relationship between rated power of main engine, propeller design diameter and water flow speed

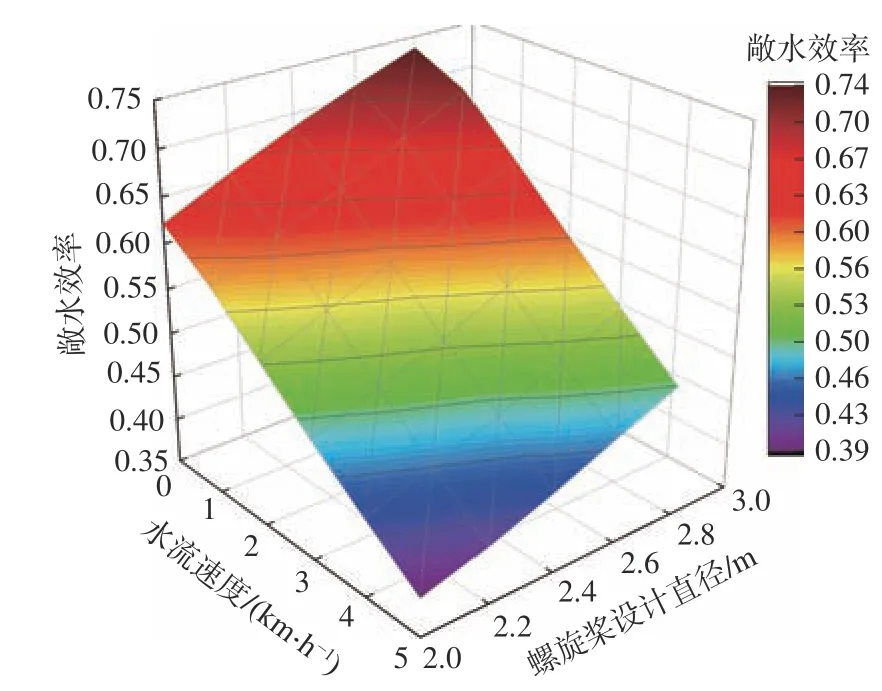
圖6 敞水效率、螺旋槳設計直徑和水流速度三者間關系Fig.6 Relationship between open water efficiency, propeller design diameter and water flow speed

以設計航速為18 km/h，螺旋槳直徑為2.2 m的輸入對7 500 t散貨船進行設計，得到船舶逆水上行和順水下行時的功率需求與敞水效率對比分別如圖7、圖8所示。

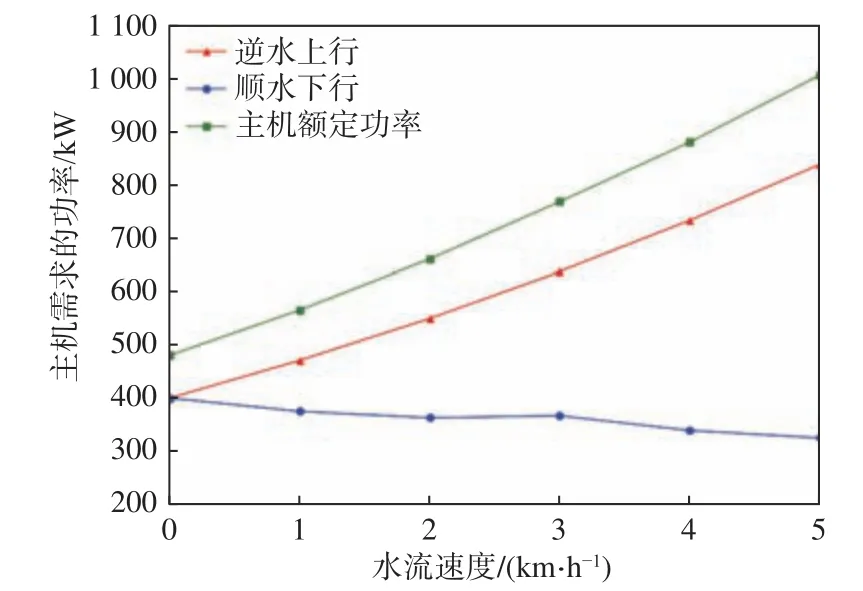
圖7 螺旋槳直徑不變時的功率需求圖Fig.7 Power demand diagram of propeller when the diameter of propeller is constant

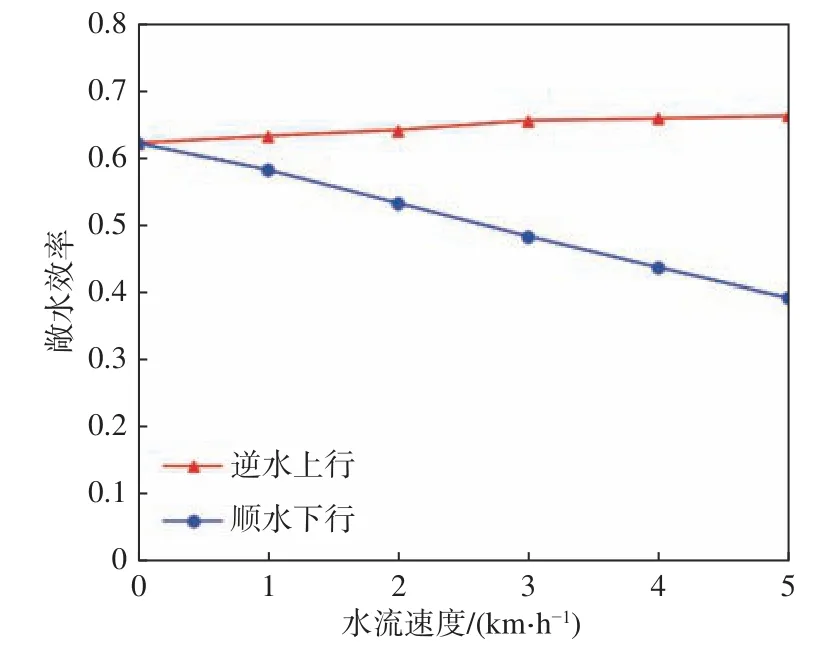
圖8 螺旋槳直徑不變時的效率對比圖Fig.8 Efficiency comparison diagram when the diameter of propeller is constant

在不同的水流速度（0，1，2，3，4，5 km/h）下，相應增加螺旋槳的設計直徑（分別取2，2.2，2.4，2.6，2.7，2.8 m）進行分析，得到船舶逆水上行和順水下行時的功率需求與敞水效率對比分別如圖9、圖10所示。

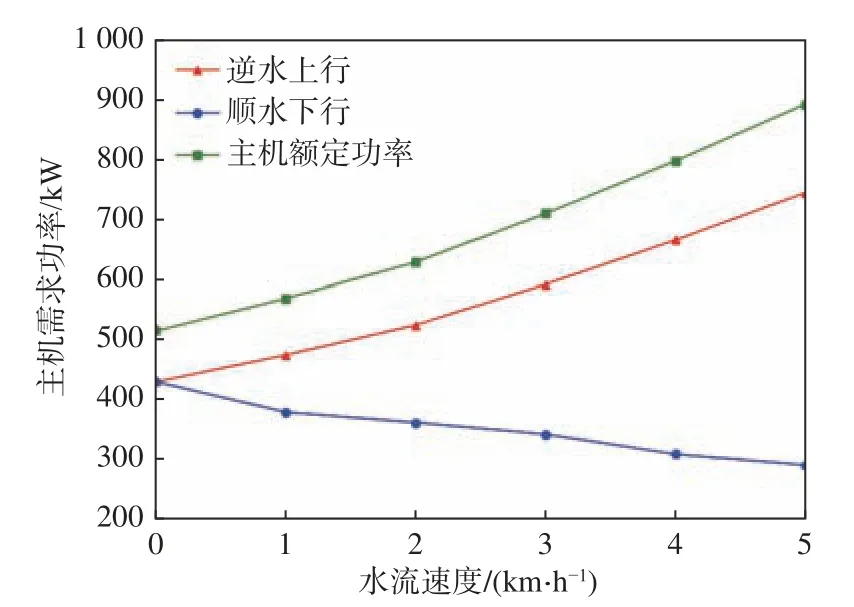
圖9 螺旋槳直徑變化時的功率需求圖Fig.9 Power demand diagram of propeller when the diameter of propeller is changed

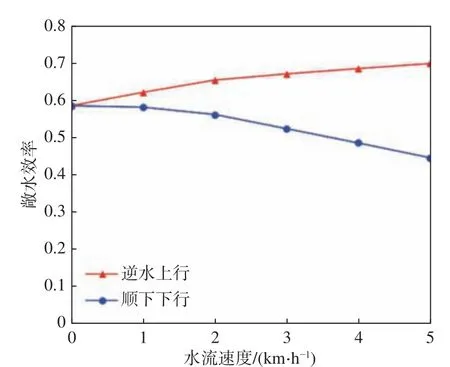
圖10 螺旋槳直徑變化時的效率對比圖Fig.10 Efficiency comparison diagram of propeller when the diameter of propeller is changed

對比圖7與圖9，發現在螺旋槳直徑變化的情況下，主機需求的功率和額定功率比螺旋槳直徑不變情況下的要低。對比圖8與圖10，發現在逆水上行時，隨著水流速度的增加，螺旋槳直徑變化情況下螺旋槳敞水效率的增長速度比螺旋槳直徑不變情況下的更快；在順水下行時，隨著水流速度的增加，螺旋槳直徑變化情況下螺旋槳敞水效率的降低速度比螺旋槳直徑不變情況下的更緩慢，其效率更高。由以上分析結果可知，若依據傳統的方法對內河船舶進行船?機?槳匹配設計，得到的設計參數無法很好地適配內河的各種工況。綜上所述，水流速度（工況）對內河船舶推進系統設計的影響較大，在內河多工況情況下，采用傳統方法設計出的參數所達到的效果并不理想。因此在內河船舶船?機?槳匹配設計中，應該考慮水流速度的影響，并將螺旋槳直徑和航速作為設計變量進行設計。

3 多目標優化問題建模

3.1 內河船舶船?機?槳匹配問題分析

傳統方法通常是以推進系統的效率為目標，而忽視了不同運行工況差異所帶來的經濟性和燃油消耗等方面的問題。針對內河船舶推進系統的設計，應充分考慮內河的多工況問題，所設計出來的主機功率、螺旋槳直徑和其他設計參數應使船舶在全工況運行周期內推進系統的效率和成本均處于最優值。上節在多種工況下，使用傳統的船?機?槳匹配設計方法對內河船舶進行了船?機?槳匹配計算，得出應將螺旋槳直徑和設計航速作為設計變量進行匹配計算，而非作為設計輸入的結論。因此，本節將把內河船舶逆水上行和順水下行時的設計航速與螺旋槳直徑作為設計變量，在Python語言環境下使用Geatpy庫建立內河船舶船?機?槳匹配多目標優化模型，其框架圖如圖11所示。

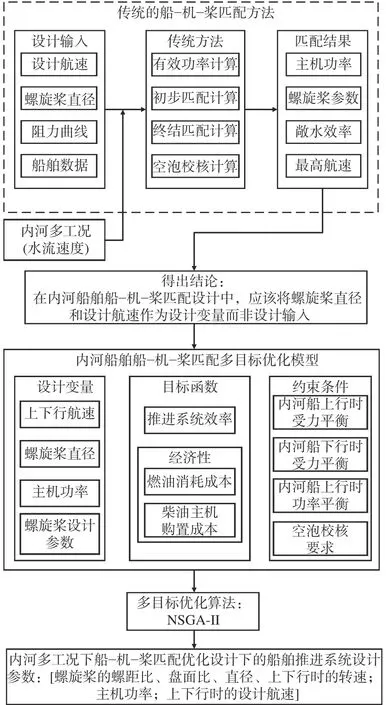
圖11 內河多工況下船?機?槳匹配優化設計框圖Fig.11 Framework of optimization design for ship-enginepropeller matching under multiple conditions in inland water

3.2 設計變量

對于內河船舶推進系統的設計，應考慮水流速度對船舶逆水上行和順水下行運行工況的影響。傳統方法將航速和螺旋槳直徑作為設計輸入，只能滿足船舶在逆水上行時的要求，而在順水下行時會出現柴油機利用率不足、燃油消耗高和推進系統效率低等問題。因此，本文將以螺旋槳螺距比P/D、盤面比AE/AO、船舶逆水上行和順水下行時的螺旋槳轉速n1，n2、螺旋槳直徑D、船舶逆水上行和順水下行時的設計航速V1，V2，以及主機輸出功率Ps為設計變量X。

X=[P/D，AE/AO，n1，n2，D，V1，V2，Ps]

3.3 目標函數

3.3.1 推進系統效率

船體、主機和螺旋槳形成一個能量平衡系統[9]，其中主機為能量源，能量在三者之間傳遞，如圖12所示。

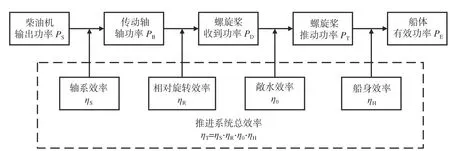
圖12 船舶推進系統功率傳遞示意圖Fig.12 Schematic diagram of power transfer of ship propulsion system

船舶推進系統總效率ηT[10]由下式求得：

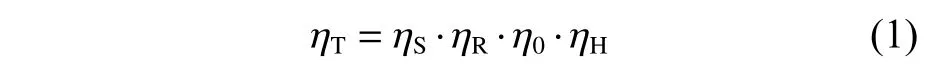
其中，軸系效率ηS一般取值0.96～0.995，相對旋轉效率ηR一般取值0.98～1.07。船身效率ηH由下式得到：

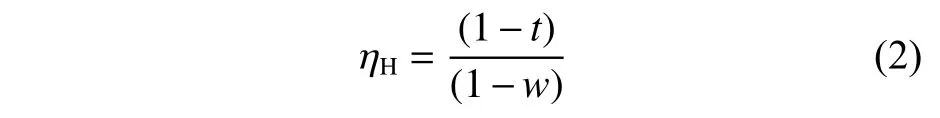
螺旋槳的敞水效率η0可由下式求得：

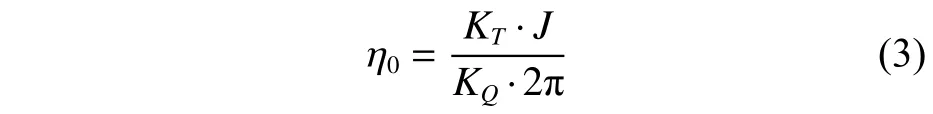
對于B系列螺旋槳，J，KT，KQ可由下列回歸公式[11]計算得到：

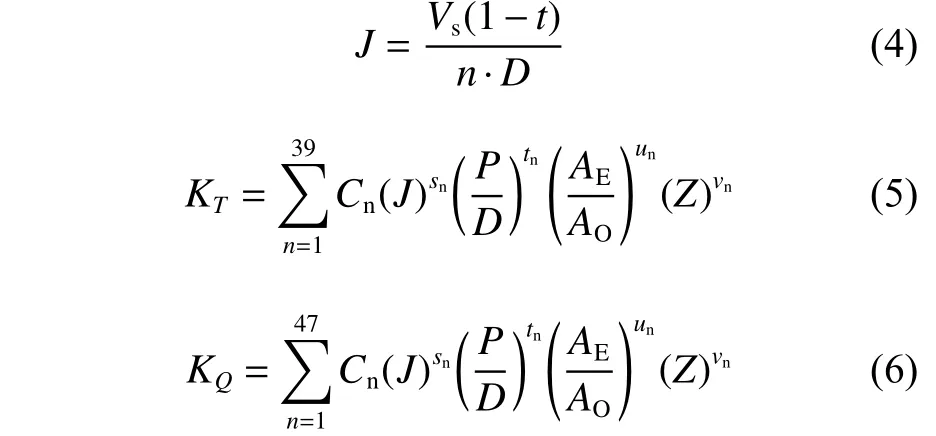
式中：Vs為船舶航速，m/s；Cn，sn，tn，un，vn為B系列螺旋槳KT，KQ多項式的各項系數；Z為槳葉數。

3.3.2 經濟性

1） 燃油消耗成本。

對于內河船舶，以一個上、下行周期內的燃油消耗量與輕油價格的乘積作為其燃油消耗成本。

對于柴油機，其燃油消耗率（SFOC）是關于柴油機使用率的函數，如圖13所示。燃油消耗率g可由下式求得：

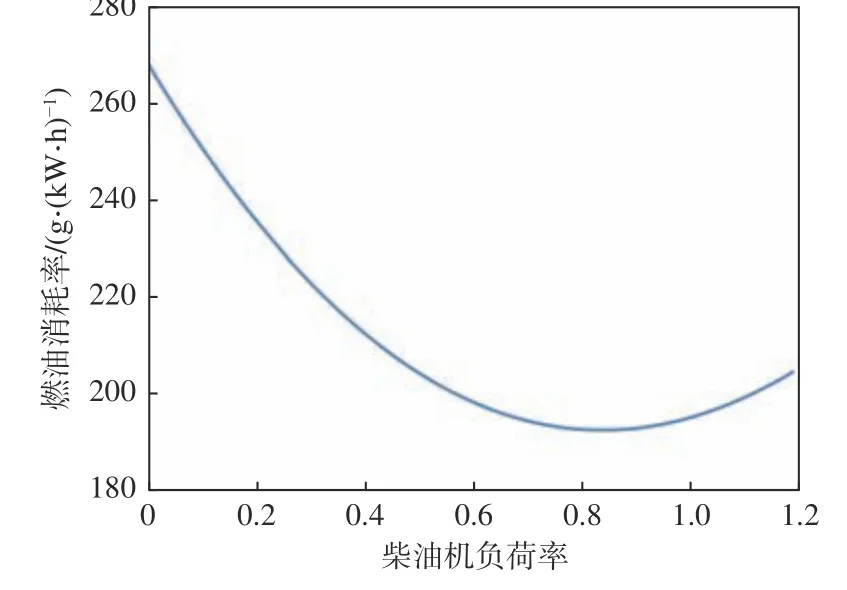
圖13 燃油消耗率與柴油機負荷率之間的函數關系Fig.13 Functional relationship of SFOC-diesel load percentage

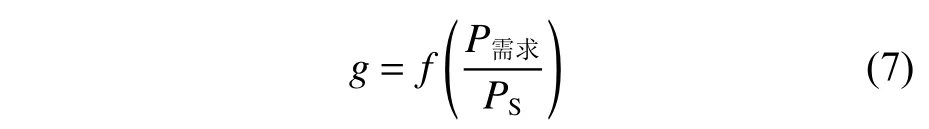
式中，P需求為船舶在運行過程中對主機功率的需求。

輕油的價格為0.5萬元/t，則燃油的消耗成本y1可由下式求得：

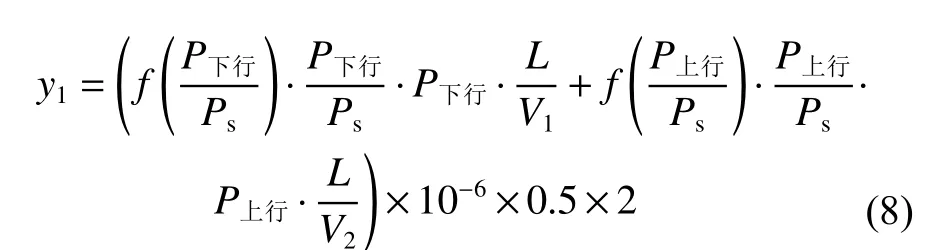
式中：P上行，P下行分別為船舶在逆水上行和順水下行工況運行時的主機功率需求；L為航程。

2） 柴油機購置成本。

內河船用柴油機的價格一般為0.6萬元/kW，則柴油主機的購置成本y2可由下式求得：

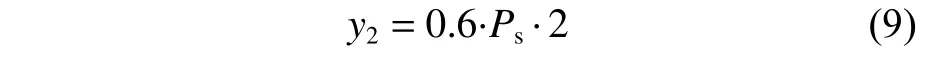
3.4 約束條件

根據船舶推進系統的運動學關系[12]（螺旋槳產生的推力與船舶阻力平衡）及能量守恒（螺旋槳負載與柴油機輸出功率平衡），可以得到3個約束條件：

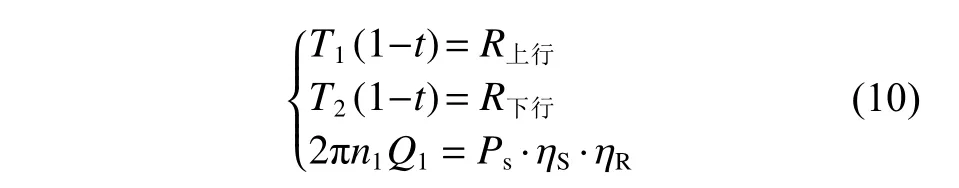
其中：

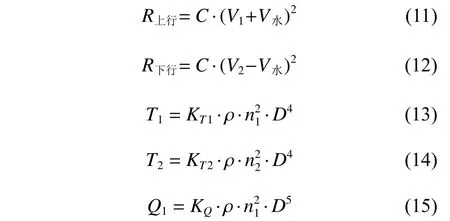
以上式中：T1，T2分別為船舶上行和下行時螺旋槳產生的推力；R上行，R下行分別為船舶上行和下行時的船舶阻力；Q1為船舶上行時螺旋槳產生的扭矩；C為船舶阻力系數。

因螺旋槳需要滿足空泡要求，因此還需要在算法中添加有關盤面比空泡校核的約束條件，從而保證所設計螺旋槳的盤面比滿足空泡校核要求，即螺旋槳盤面比大于不發生空泡所要求的最小盤面比。空泡校核的經驗公式采用keller公式[13]。則第4個約束條件如下所示：

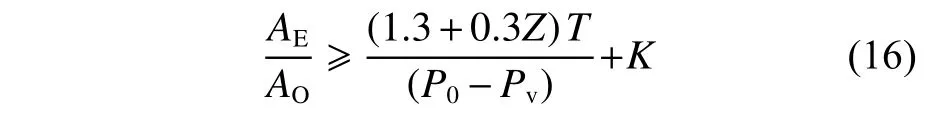
式中：P0為螺旋槳軸中心的靜壓力；Pv為水的汽化壓力；K為系數（單槳船為0.2，高速雙槳船為0，其他種類的雙槳船為0.1）。

3.5 多目標優化模型

考慮內河船舶的經濟性（一個周期的燃油消耗成本和船舶主機購置成本）和推進系統效率的多目標優化模型定義如下：

3.6 多目標優化算法

由于各個優化目標之間的相互競爭和沖突關系，多目標優化的解并不唯一的，而是一組均衡解，即最優非劣解或Pareto最優解集[14]。NSGAII算法是目前最流行的多目標遺傳算法之一，該算法能降低非劣排序遺傳算法的復雜性，具有運行速度快、解集的收斂性好等優點。因此，本文應用NSGA-Ⅱ算法求解式（18）中的多目標Pareto解。其流程如圖14所示。圖中，Gen為進化代數，Rt為父代、子代合并后的種群，Pt+1為新的父代種群，Np為種群中支配個體p的個體數。

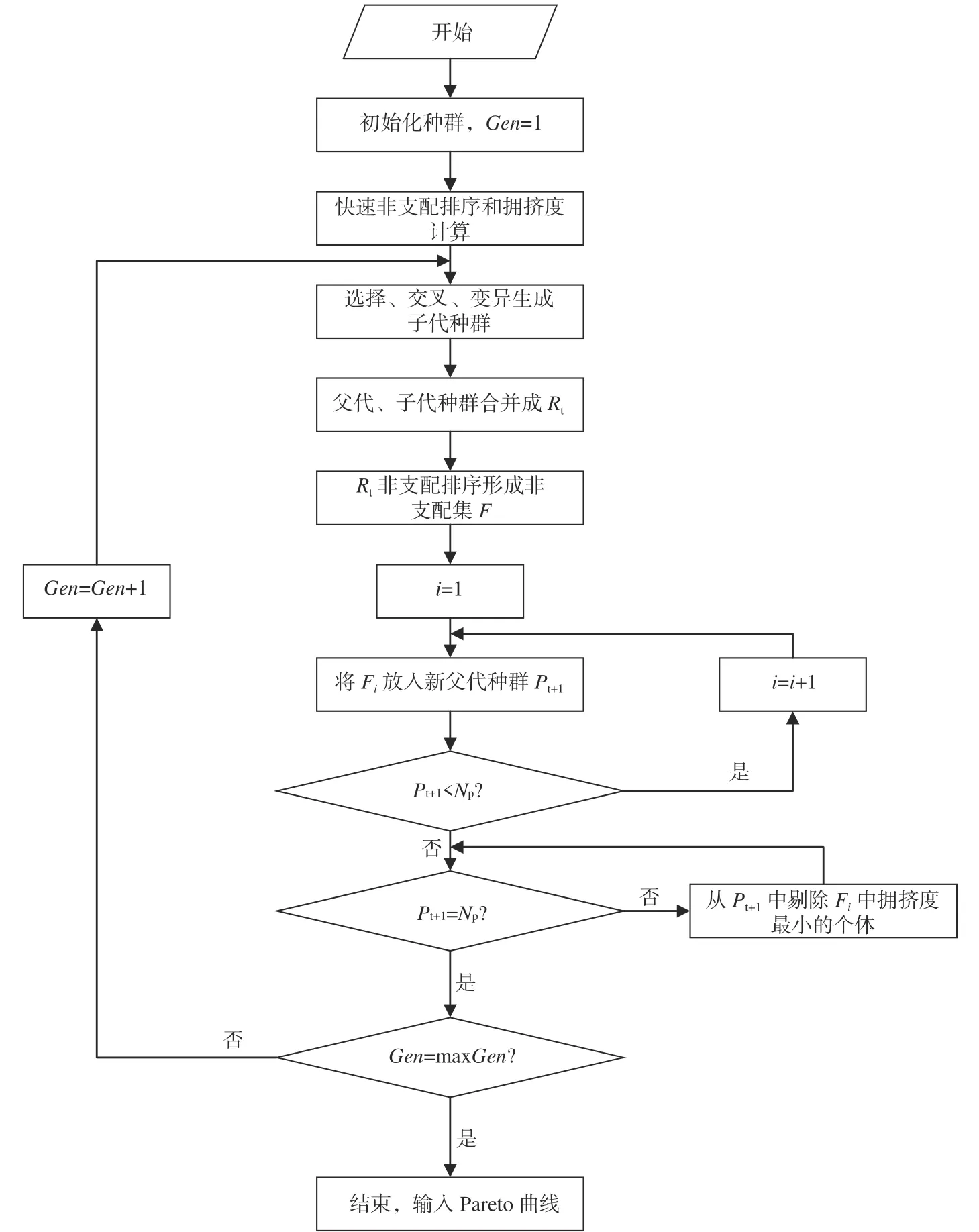
圖14 NSGA-Ⅱ算法流程圖Fig.14 NSGA -Ⅱ algorithm flow chart

4 算例分析

本文將以航行于武漢—上海之間的7 500 t散貨船為例，采用B系列五葉螺旋槳對其進行設計。NSGA-Ⅱ算法參數設置如表2所示。

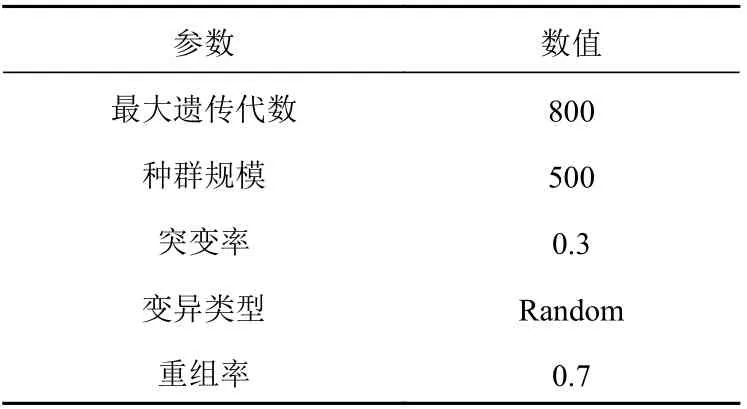
表2 NSGA-II算法參數Table 2 Parameters of NSGA-II algorithm

在通過python語言建立的內河多工況下船?機?槳匹配多目標優化模型中，調用Geatpy庫中的NSGA-II算法包，設置NSGA-II算法參數，進行多目標優化。共進行了5次實驗，優化結果如表3所示（表中，f2為柴油機購置成本，f1為燃油消耗成本）。由表可以看出，只有第5次實驗的優化效果不太理想，其中只推進系統的效率有明顯提高，經濟性目標函數中2個指標的優化效果均不明顯，其結果不符合多目標優化原則，應予以舍棄；第1，2，4次實驗的優化結果較為理想，2個目標函數（推進系統總效率和經濟性）相比原始值均有較大提高；第3次實驗結果中柴油主機購置費用f1的優化不太明顯，但其他目標函數，如推進系統效率和燃油消耗成本的優化效果均較好，尤其是燃油消耗成本，降低的幅度較大。因此，可以考慮采用第3次實驗結果。5次的優化結果表明，NSGA-Ⅱ算法是一種有效的解決多目標優化問題的方法，能夠快速找出Pareto前沿解。內河多工況下的船?機?槳匹配優化設計方法能夠較為穩定地解決內河船舶在多工況下的推進系統設計問題。

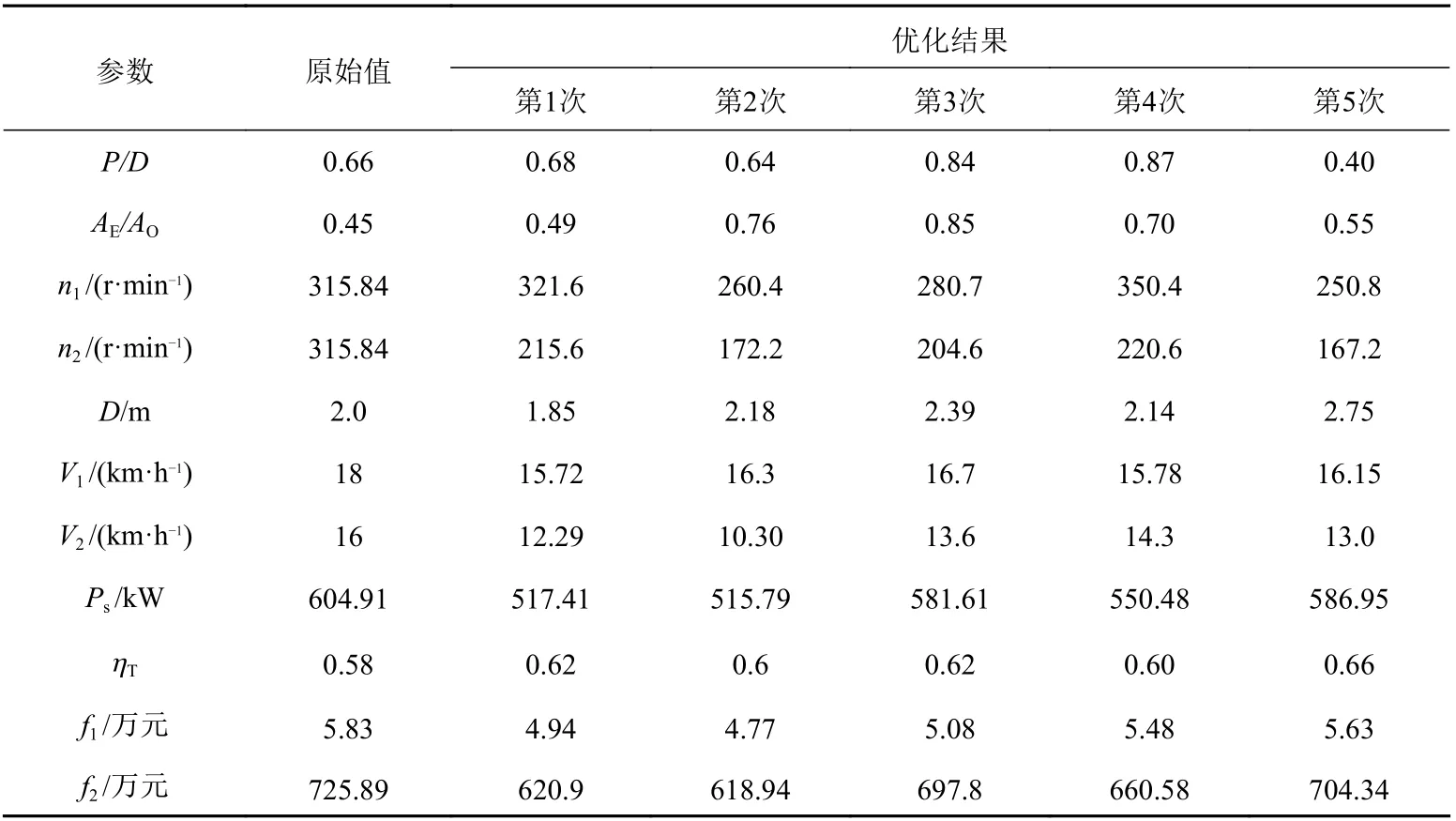
表3 原始值與優化結果的對比（Pareto前沿解）Table 3 Comparison of initial values and optimal solutions (Pareto front)

以第2次優化結果為例，在經濟性目標函數中，燃油消耗成本f1降低了18.1%，柴油機的購置成本f2降低了14.73%，船舶推進系統效率提高到了0.6。初始方案與優化方案的敞水特性曲線如圖15所示。

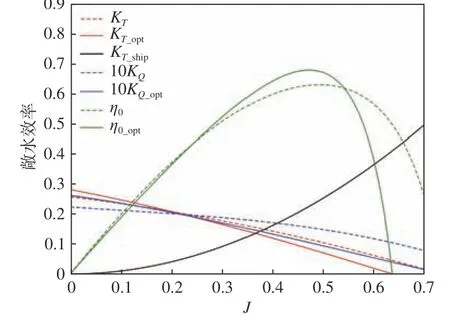
圖15 初始方案與優化方案的敞水特性曲線Fig.15 The open water performance curves of the initial and optimization scheme

5 結 語

本文提出了一種基于NSGA-Ⅱ算法、考慮內河多工況的船?機?槳匹配設計方法。優化的目標函數有2個：一個是船舶推進系統的總效率，另一個是經濟性（燃油消耗成本和主機購置成本）。文章首先對船?機?槳匹配設計理論進行分析，得出了船體、主機和螺旋槳各設計參數之間的相互影響關系；然后使用傳統的船?機?槳匹配設計方法，在不同工況下對內河船舶的推進系統進行了設計，隨后又對內河船的機?槳匹配問題進行建模，得到了需要求解的數學模型；最后，設置NSGA-Ⅱ算法參數，以內河7 500 t散貨船為例進行了多目標優化。基于多次優化結果，得到以下主要結論：

1） 本文研究的內河多工況船?機?槳匹配優化設計方法充分考慮了內河船上、下行工況對船?機?槳匹配的影響，其以推進系統的總效率和經濟性為目標函數，進行了多目標優化設計，結果顯示采用本文方法得到的優化設計參數（主機功率、螺旋槳螺距比、螺旋槳盤面比、螺旋槳直徑、船舶上下水航速）能夠更好地適配內河的通航環境，可提高船舶運營的經濟性。

2） 內河多工況船?機?槳匹配優化設計方法能適配內河船舶推進系統的多目標優化問題，可為內河船舶的船?機?槳選型、匹配優化設計和實際系統優化運行提供理論方法與技術支撐。