基于模糊自適應的固態變壓器逆變級改進LADRC控制

馬幼捷，張 彤，周雪松

（1.天津理工大學天津市復雜系統控制理論與應用重點實驗室，天津 300384；2.天津理工大學電氣電子工程學院，天津 300384）

隨著全球經濟的發展，全世界對能源的需求越來越高，傳統化石能源日益枯竭，新能源和可再生能源發電系統也因此在工業應用中得到了推廣和利用[1]。固態變壓器 SST（solid-state transformer）為各種直流或交流分布式電源、非線性設備等提供了進入電力系統的友好接口，它不僅可以實現可再生能源的即插即用，而且可以通過電力電子轉換技術實現電力系統中的電壓轉換和雙向能量傳輸[2-3]。改善了電能質量，提高了工業效率，增強了系統可靠性。

固態變壓器的逆變級直接與風力發電機、用戶側負載、電動機、燃氣輪機等連接，實現電能的雙向傳輸，其輸出波形質量直接決定著固態變壓器的運行品質[2-4]。固態變壓器逆變級的本質是非線性系統，同時又有大量分布式能源接入，現在常用的基于比例-積分PI（proportion-integral）調節器的電壓電流雙閉環控制策略已經越來越難達到滿意的效果，因此，構想一種抗擾性強的電壓控制方案是有意義的。

針對非線性、耦合強、時滯大等不確定因素，韓京清[5]結合傳統PID控制器和現代控制理論提出了非線性自抗擾控制ADRC（active disturbance rejection control），但傳統ADRC結構較為復雜，參數多且難以調整，不太利于工程應用[6]。基于此，高志強[7]簡化了結構，提出了線性自抗擾控制LADRC（linear active disturbance rejection control），大大減少了計算量，具有一定的工程實用價值。但LADRC在簡化參數的同時也降低了控制性能[8-11]。為解決上述問題，文獻[8]在傳統LADRC中加入超前校正環節，對里面的觀測帶寬進行了改善，提高了觀測精度但使參數設計變得復雜。

針對負載側三相交流電壓控制問題，本文提出了一種改進線性自抗擾控制，考慮了LESO對總擾動估計時的誤差并給予補償，后將改進LADRC與模糊自適應系統結合實現參數自整定，最終提出了FI-LADRC控制策略。第1節建立了固態變壓器逆變級數學模型，對非線性系統加入小擾動信號進行線性化處理；第2、3節對FI-LADRC進行了設計和分析；第4節通過仿真驗證了該策略的參考價值，在不同類型的負載擾動下，保證了輸出三相交流電壓的穩定且符合國家標準；最后進行了總結。

1 固態變壓器逆變級建模

固態變壓器逆變級電路拓撲如圖1所示。圖1中：Udc為逆變級輸入直流側電壓；Sij(i = a,b,c;j=p,n)為逆變級開關函數；ia、ib、ic為逆變級三相輸出電流；R、L、C分別為寄生電阻、濾波電感和濾波電容；uAB、uBC、uCA為負載側三相線電壓；iA、iB、iC為三相負載電流。

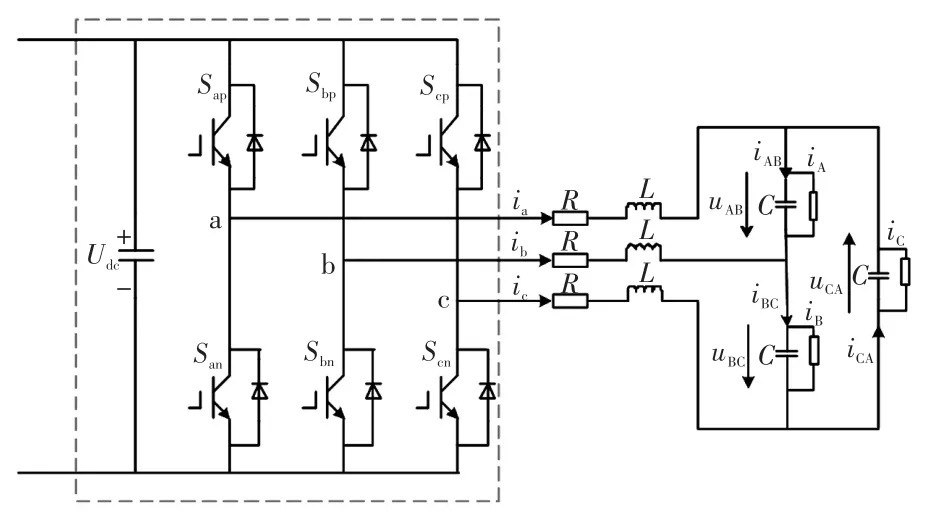
圖1 固態變壓器逆變級電路拓撲Fig.1 Circuit topology of inverter stage of SST

式中：dd、dq為占空比d-q軸分量；id、iq為逆變級輸出電流d-q軸分量；ud、uq為逆變級負載線電壓d-q軸分量；iLd、iLq為逆變級負載電流d-q軸分量；ω為電網角頻率。

對式（6）進行小擾動線性化處理，將其中的擾動參量分離得到d-q軸坐標系下的小信號模型為

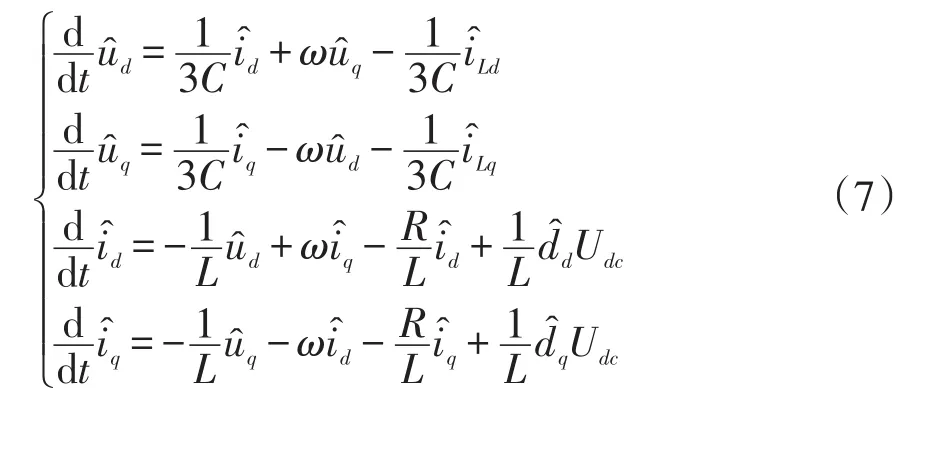
2 FI-LADRC的設計

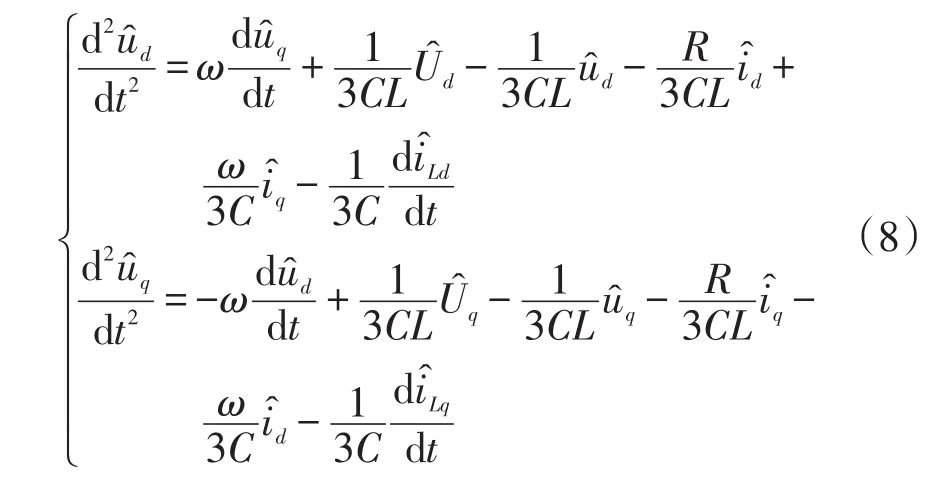
根據被控對象階數，在d-q軸分別設計一個二階LADRC代替傳統的雙閉環控制。d軸q軸之間的耦合被當成擾動看待時，兩軸LADRC結構相同，因此下文主要以d軸為例來進行設計和分析。系統的整體控制結構如圖2所示。

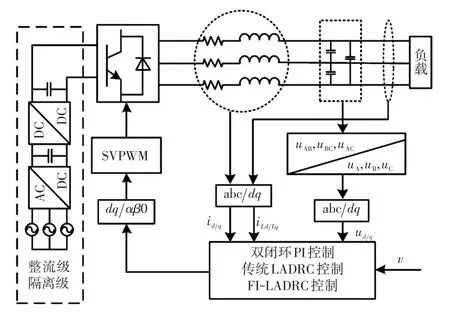
圖2 系統整體控制結構Fig.2 Overall control structure of system

2.1 LESO設計

由于LADRC不需要依賴受控對象的特定數學模型，所以受控對象的微分方程的通用形式為

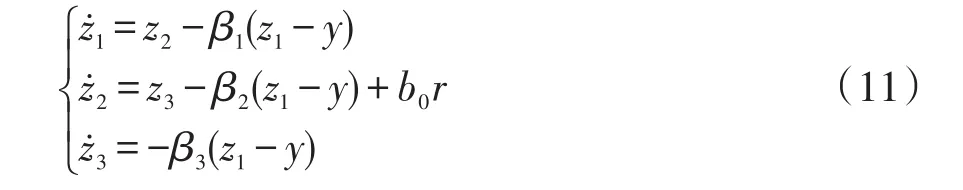
只要增益 β1、β2、β3的選擇適當，LESO就能實時跟蹤式（10）中的各變量，z1、z2、z3分別為狀態變量。

2.2 基于LESO估計誤差補償的改進控制率設計

結合式（10）和（11），定義LESO的估計誤差為e1=z1-y,e2=z2-x2,e3=z3-f（f為總擾動），將式（11）與（10）相減，得到估計誤差的狀態空間表達式為

圖3是改進LADRC的結構框圖，引入了給定參考信號的一階微分，減小了穩態誤差[9]；在控制率上做出改進，對總擾動的估計誤差進行補償，提高系統的抗擾動性能。

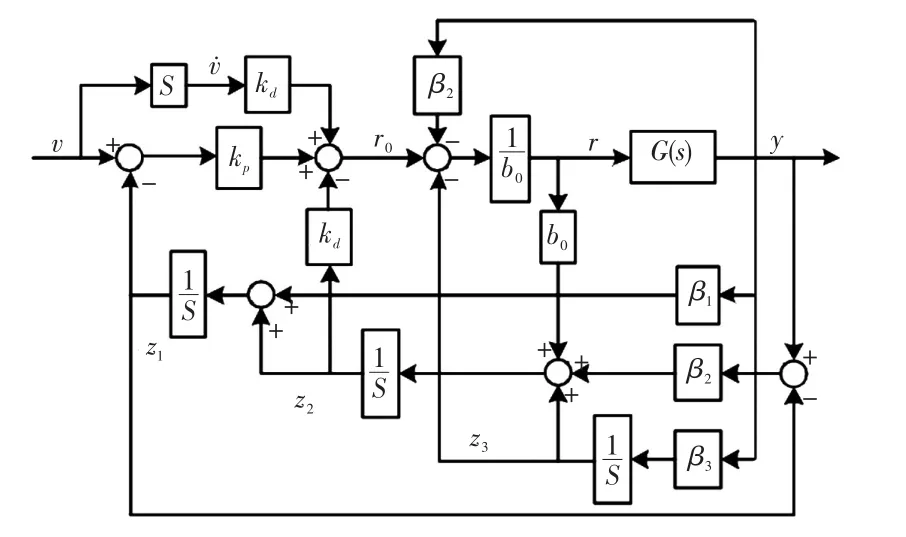
圖3 改進LADRC結構Fig.3 Improved LADRC structure

2.3 模糊自適應反饋控制率的設計

模糊自適應控制不需要建立被控系統的精確數學模型，利用模糊規則和隸屬函數來減少數據的不確定性，該方法先將多個隸屬度函數組成的模糊集在[0，1]的范圍內進行模糊化，在推理步驟中將輸入信號與模糊規則進行聚合，最后對推理結果進行反模糊化，并輸出一個清晰的值[12-15]。模糊自適應系統的一般結構如圖4所示。

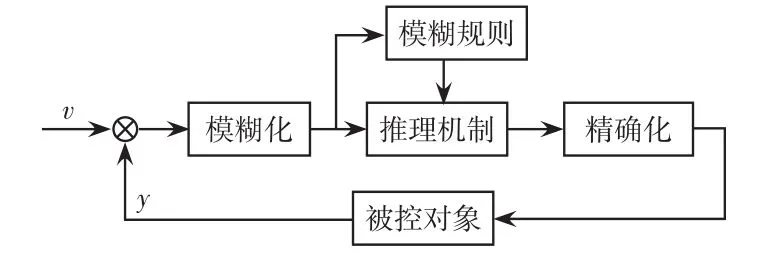
圖4 模糊自適應系統的一般結構Fig.4 General structure of fuzzy adaptive system

但是模糊自適應控制對采集到的信息進行模糊化處理的過程，會造成被控對象的控制精度下降，動態性能降低[13]。因此，將其與改進線性自抗擾結合，設計了新型控制策略FI-LADRC，充分利用兩種策略的優勢，實現系統的高性能控制。FILADRC控制原理結構如圖5所示。

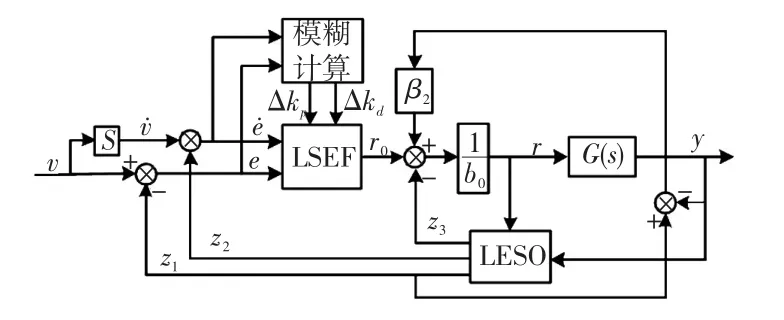
圖5 模糊改進線性自抗擾控制器結構Fig.5 structure of FI-LADRC controller

其模糊控制規則表如表1所示，輸出表面的隸屬函數如圖6所示。

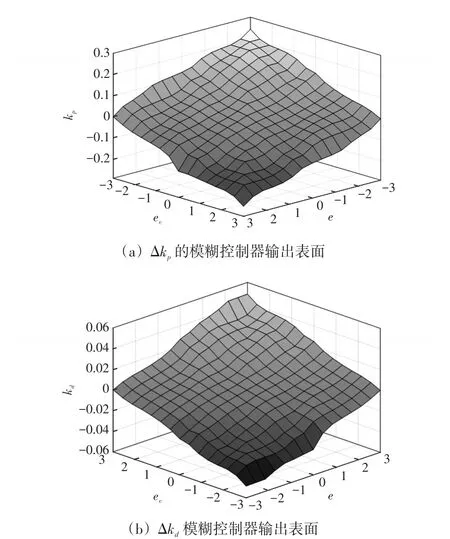
圖6 模糊控制器輸出表面Fig.6 Output surface of fuzzy controller

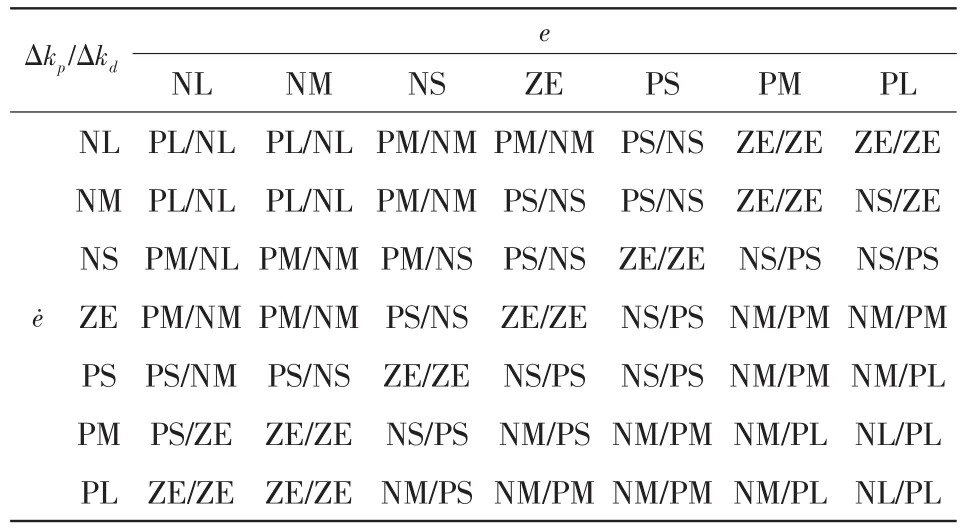
表1 Δkp和Δkd的模糊控制規則Tab.1 Fuzzy control rule for Δkpand Δkd

結合式（11）、（14）、（22）、（23）和（24），將模糊自適應系統與改進LADRC結合的控制器設計為

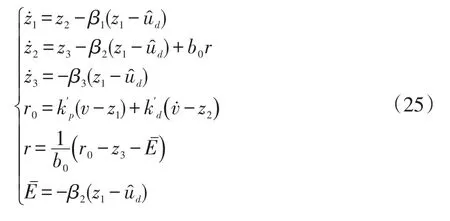
2.4 參數設計

用極點配置法對觀測器和控制器參數進行設計，求得LESO的特征方程為

選擇一個極點在左半平面，為了簡單，把所有極點都選在-ω0處，則有

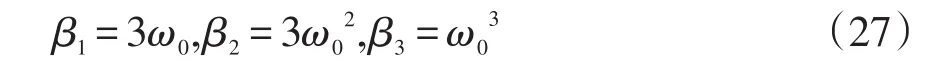
類似地，把閉環極點都放在ωc處，式（14）參數為

此時，二階LADRC只需要合理地調整控制器帶寬ωc、觀測器帶寬ω0就可以獲得良好的控制效果。對于常見的大部分工程對象，一般取ω0=(3 ～5) ωc。

3 FI-LADRC的性能分析

控制的三大要素是跟蹤性、抗擾性和穩定性，分別從這三方面對所提出的FI-LADRC控制策略進行分析。

將式（14）、（19）和（22）代入式（23），可得

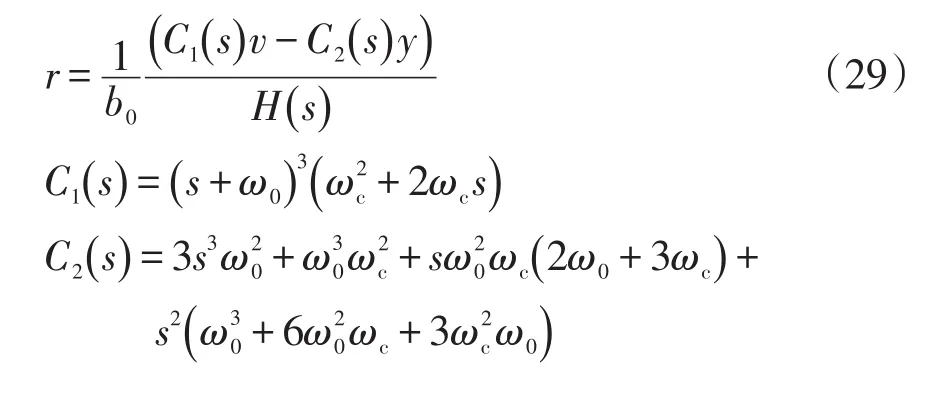
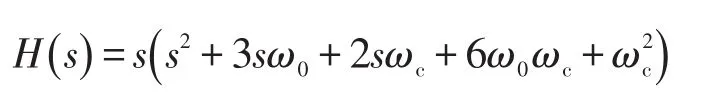
閉環系統的結構如圖7所示。

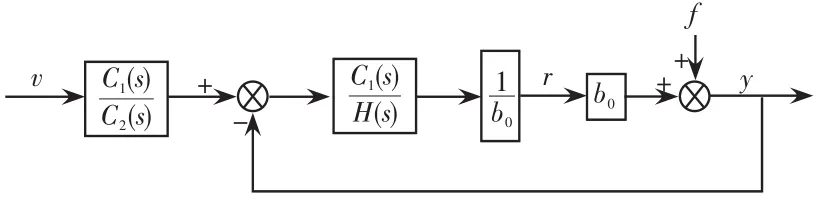
圖7 簡化系統結構Fig.7 Simplified system structure

被控對象模型記為

3.1 跟蹤性分析

從式（31）可以直觀地看出，系統輸出由跟蹤參考信號v的跟蹤項和擾動項組成，表示跟蹤項的傳遞函數為

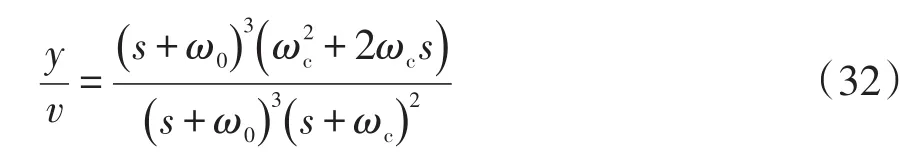
與傳統LADRC控制下的傳遞函數相比，系統跟蹤性能對比如圖8所示。

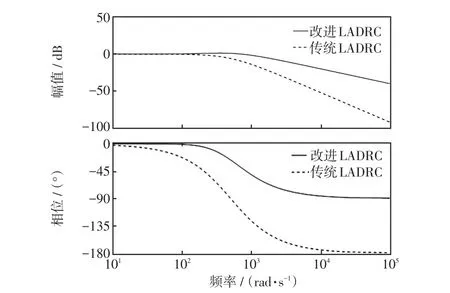
圖8 系統跟蹤性能對比Fig.8 Comparison of system tracking performance

由于系統復現輸入信號的能力取決于系統的幅頻特性和相頻特性，從Bode圖看出，改進LADRC控制對中高頻給定信號的通過性能更好，相位滯后變小；在同樣的帶寬下，改進LADRC比傳統LADRC有更大的剪切頻率，其響應速度更快。

3.2 抗擾性分析

由式（31）可知，擾動項的傳遞函數為

圖9是改進LADRC與傳統LADRC擾動項傳遞函數伯德圖，從圖9中可以看出，改進LADRC的帶寬增加，抗擾能力增強。

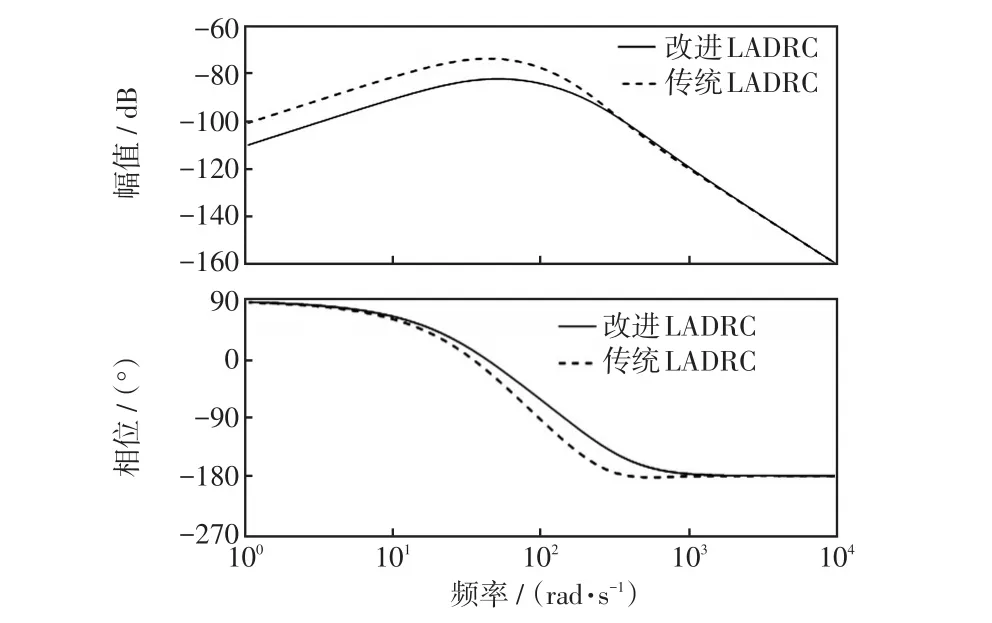
圖9 改進LADRC與傳統LADRC擾動項對比Fig.9 Comparison of disturbance term between improved and traditional LADRCs

同樣，從式（33）中看出，系統輸出的擾動項與ω0、ωc有關，選取ωc=10,ω0=10、20、30時的頻率特性如圖10（a）所示；取 ω0=10,ωc=10、20、30，可得其頻域特性曲線如圖10（b）所示。由圖10可知，增加ωc和ω0可使擾動增益減小，系統抗擾能力增強。

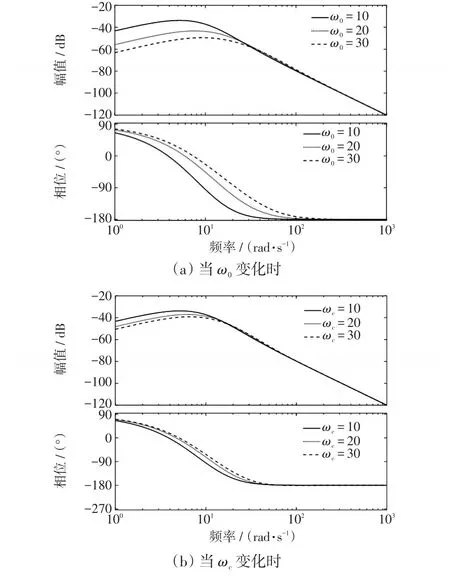
圖10 改進LADRC擾動項的幅相頻率特性Fig.10 Amplitude-and phase-frequency characteristics of disturbance term in improved LADRC

3.3 穩定性分析

結合式（10）、式（11）和式（27），將LESO寫為

根據李亞普諾夫漸近穩定性的定義，FILADRC是漸進穩定的。

4 仿真驗證

為了驗證模糊自適應系統與改進LADRC結合的正確性和有效性，應用Matlab/Simulink平臺建立了固態變壓器逆變級仿真模型，建模用到的主要參數如表2所示。

表2 仿真部分的參數Tab.2 Simulation parameters

分別采用傳統雙閉環PI控制、傳統LADRC控制和文中提出的改進控制對逆變級輸出波形進行比較。

（1）工況一：驗證抑制諧波的良好性能。

對于逆變級而言，輸出電壓波形是否平滑決定著電能質量的好壞。波形畸變會在電路運行過程中產生附加損耗，對負載有一定的影響，嚴重時會減少設備的使用壽命；往往高精密儀器、用電設備對電能質量要求更高，故需要更好的控制策略使輸出電壓波形諧波含量更少。

不同負載條件下，3種控制策略對諧波的抑制能力如圖11所示。在0.15～0.2 s為阻性負載，0.2～0.25 s切換為阻性和整流性相加的混合負載，0.25 s之后為整流性的非線性負載。以A相電流電壓為例，圖中標出了各種負載下的輸出電壓波形的總諧波畸變率THD（total harmonic distortion）。可以直觀地看出相較于傳統PI控制、傳統LADRC控制，提出的FI-LADRC控制策略抑制諧波能力更強。

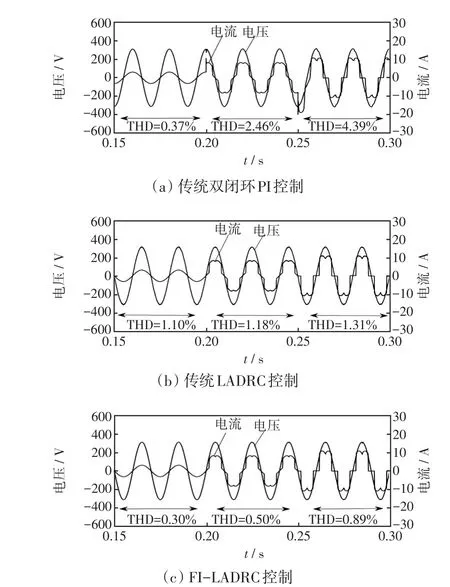
圖11 不同負載下的電壓電流波形Fig.11 Waveforms of voltage and current under different loads

通過觀察系統切換負載時的暫態特性，可以比較出控制策略的優劣。

（2）工況二：驗證線性負載突變時的瞬態性能。

在阻性負載的基礎上進行負荷突增和負荷突減試驗情況如圖12所示，為了方便觀察，選取了旋轉坐標系下的d軸圖。圖12（a）為負載突變的整體圖，在0.1 s時負荷突增50%，0.2 s時負荷突減50%。圖12（b）為加載時的放大圖，可以看出突增時PI控制下的電壓恢復時間為1.4 ms，峰谷差為15.3 V；傳統LADRC控制下恢復時間為0.8 ms，峰谷差10.7 V；但FI-LADRC控制下的電壓恢復時間只有0.2 ms，最大差值只有5.1 V。圖12（c）為減載時的放大圖，PI控制時電壓出現明顯波動，持續時間為0.3 ms，最大差值為5.6 V；傳統LADRC控制時存在上下2.5 V的小幅度波動；而FI-LADRC控制的在突減50%的擾動下波形幾乎不發生畸變。因此，驗證了所提出策略具有更好的魯棒性以抵抗外部干擾。

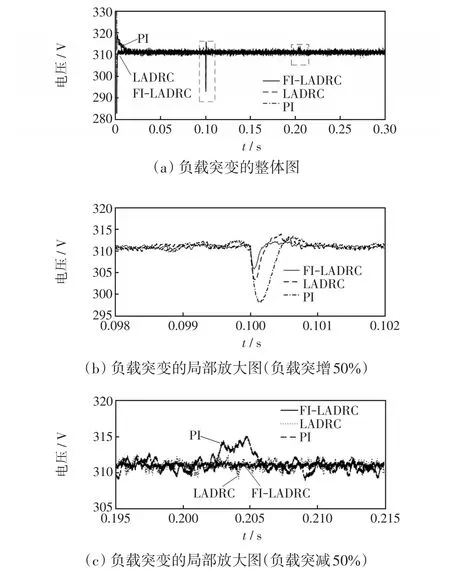
圖12 阻性負載突變時d軸電壓波形Fig.12 Waveforms of d-axis voltage under resistive load mutation

（3）工況三：驗證非線性負載突增時的動態響應。

為了驗證FI-LADRC具有更好的抗擾性，在系統帶整流性負載運行過程中突增負載作為擾動，3種控制策略下突變瞬間的電壓、電流波形如圖13所示。可以看出非線性負載在PI控制下的波形畸變嚴重，突變前后畸變率分別為2.47%和4.25%；傳統LADRC控制的波形相對有所好轉，但波形并不光滑，突變前后的畸變率有所下降，分別為1.08%和1.29%；FI-LADRC控制性能最好，波形較為光滑，突變前后畸變率為0.47%和0.89%。因此，文中提出的控制策略性能更好。

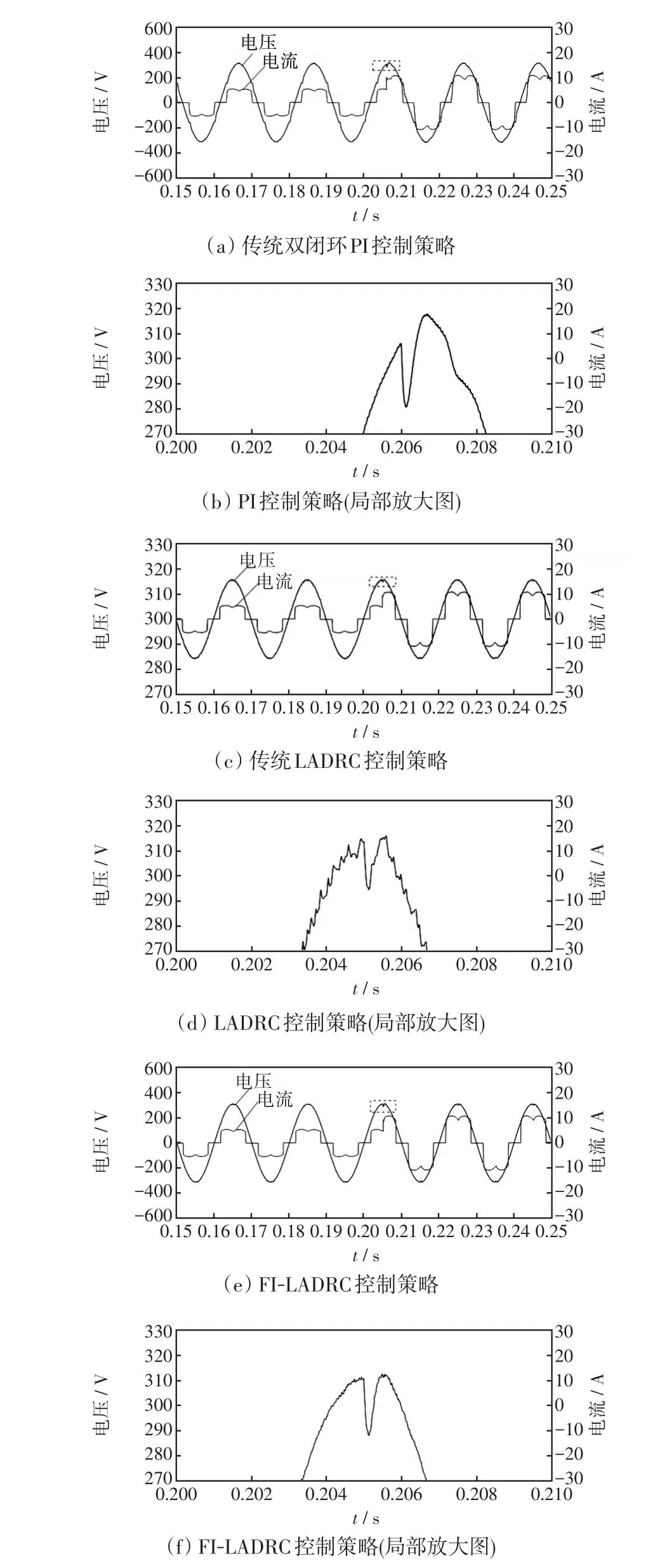
圖13 非線性負載突變電壓電流波形Fig.13 Waveforms of voltage and current under nonlinear load mutation

5 結語

為了提高固態變壓器逆變級在負載擾動時輸出電壓的穩定性，設計了一種改進LADRC單環控制策略；為了進一步減少控制器設計的計算量，實現系統自動尋優的需求，與模糊自適應系統結合，提出了FI-LADRC。文中設計的控制策略考慮了LESO的估計誤差，使閉環系統更貼近目標函數，采用模糊邏輯理論根據系統的偏差不斷調整帶寬參數，實現控制器參數的自整定，該策略融合了模糊控制自適應強和LADRC魯棒性強的優點。通過理論分析和多工況下的仿真驗證，表明所提出的電壓控制策略對系統動態干擾具有較強的魯棒性，且穩態和動態性能良好。