復雜電網下基于CSDFT-MAF-PLL的電壓同步方法

陳 偉 ，何 山 ，2

（1.新疆大學電氣工程學院，烏魯木齊 830049；2.可再生能源發電與并網控制教育部工程研究中心，烏魯木齊 830049）

以風電、光伏為代表的新能源發電并網運行，需準確獲取電網電壓的相角、頻率和幅值等信息，以提升系統故障恢復時間及并網能力[1-2]。鎖相環PLL（phase-locked loop）作為并網的關鍵環節，直接影響電力轉換系統的穩定性與可靠性[3]，其快速精準的鎖相能力對電力電子裝置并網具有十分重要的作用。

同步旋轉坐標系鎖相環SRF-PLL（synchronous reference frame PLL）在電力電子和電力系統中應用廣泛[4-5]，理想電網下，能快速準確地提取相位信息；復雜電網下，需降低鎖相環帶寬，以提高諧波抑制能力，但響應速度下降[6]。文獻[7]提出SRFPLL存在相位與頻率檢測緊密耦合問題，諧波或任何類型的故障失衡引起的誤差嚴重影響鎖相性能。文獻[8]提出附加前置解耦單元的準一階鎖相環，結合級聯延遲消去法，增強系統抗諧波能力，該前置濾波環節只適合頻率波動小的系統，復雜電網條件下效果不佳。

為克服SRF-PLL在抑制直流分量及諧波方面的不足，文獻[9]利用解耦雙同步參考坐標系鎖相環DDSRF-PLL（decoupled double SRF-PLL）提取三相電壓正、負序分量，利用解耦模塊消除擾動，但該方法結構復雜，給系統帶來一定延遲。

為克服DDSRF-PLL結構復雜和延遲問題，文獻[10]提出雙二階廣義積分器鎖相環DSOGI-PLL（double second-order generalized integrator PLL），電網畸變程度低時，能快速有效鎖定相位，但在含直流偏置及多次諧波等復雜電網下，提取的同步信號會出現較大波動。

為克服DSOGI正交信號發生器DSOGI-QSG（DSOGI-quadrature signals generator）在復雜電網下提取同步信號困難問題，文獻[11]提出結構簡便、濾波程度高的滑動平均濾波鎖相環MAF-PLL（moving average filter PLL），滑窗寬度的選取基準直接影響濾波效果及動態特性。為克服該弊端，文獻[12]提出雙滑動平均濾波鎖相環，并附加角頻率重構模塊以消除鎖相誤差，該滑窗寬度設置較大，提升了動態特性，但該鎖相環設計只針對單相系統。

滑動離散傅立葉算法SDFT（sliding discrete Fourier transform）是諧波測量中使用最廣泛的算法之一。電力系統的諧波成分通常是時變的，特別是在較長傳輸距離的弱配電網中，直接進行頻譜分析會由于泄漏和柵欄效應導致結果不準確。文獻[13]針對SDFT頻譜泄漏問題，提出建立泄漏狀態下的相角或幅值關系，間接計算電網頻率，但復雜系統對關系式本身會造成影響。

針對上述問題，文中設計思路如下：首先，為解決常規SDFT容易出現頻譜泄漏問題，提出固定滑窗-變滑窗結構的級聯型滑動離散傅立葉變換方法，后級SDFT滑窗寬度依據實時檢測的電網頻率調整，利用DFT相角特性，生成每一相虛擬正交信號，提取基波信號；其次，設計附加相位補償MAF正、負序分離模塊，既能準確濾除負序分量，又能避免因MAF階數過高造成的相位延遲；最后，仿真驗證方法有效性。

1 復雜電網多故障誤差分析

以SRF-PLL為例，分析系統在出現三相電壓不平衡、含直流偏移及多次諧波分量下的動態性能。假設：

（1）輸入信號為理想三相正弦波；

（2）在變量發生變化之前，系統已達到穩態；

（3）推導過程在時域下進行，系統視為零狀態系統。

式中：vd、vq為 d、q坐標下電壓分量；vd_dc、vq_dc為直流偏移分量在d、q坐標下產生的電壓分量；vd_U、vq_U為電壓相位不平衡在d、q坐標下產生的電壓分量；vd_h、vq_h為諧波分量在d、q坐標下產生的電壓分量；Vdc_α、Vdc_β為α、β坐標下直流偏移分量；θ為檢測的三相電壓相位角；ε為相位誤差。

由式（2）可知：由直流偏移引起的誤差具有與電網電壓相同的頻率分量；三相電壓不平衡誤差分量為2倍頻擾動分量；電網非3倍奇次諧波分量會產生6倍頻擾動誤差。理想電網下，三相電壓信號通過坐標變換轉換為dq坐標下的電壓分量，SRFPLL對信號進行處理，可快速精確地跟蹤相位，但其結構無法克服在三相電壓不平衡、含直流偏移及多次諧波污染下的擾動誤差。

2 CSDFT-QSG頻率自適應設計

2.1 CSDFT-QSG設計

DFT算法可提取電網輸入信號中的基波信號，消除鎖相外環中的諧波分量及直流分量，但需要計算完整一個周期才更新一次數據。基于樣本數據的相似性，由前一階段窗口函數的頻譜特性所生成的遞推關系，可推算出當前時刻的頻譜。SDFT算法依據固定窗口隨時間滑動提取樣本數據[14]。

由式（4）、（5）可知，輸入電網電壓信號，生成其虛擬正交信號，提取基波信號，具體結構如圖1所示。

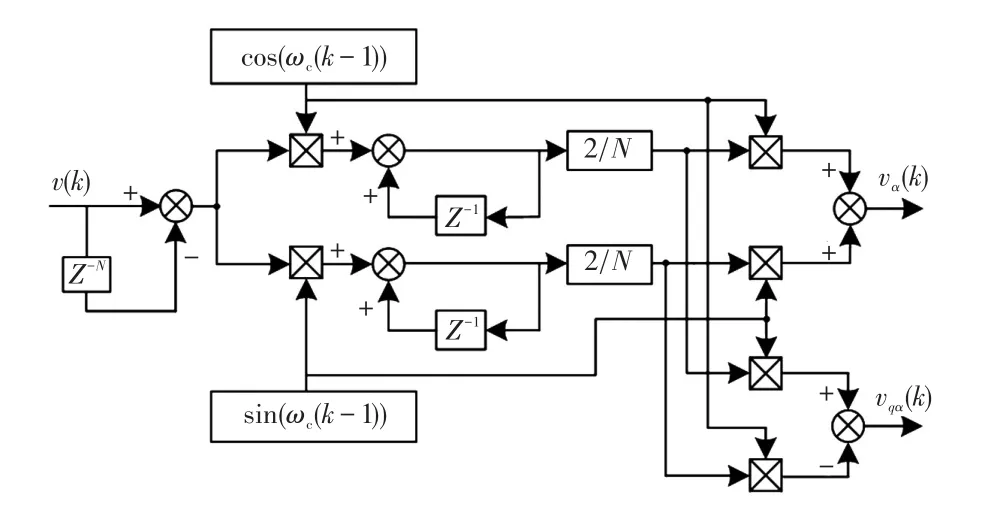
圖1 SDFT-QSG結構Fig.1 Structure of SDFT-QSG

圖1中，vα(k) 、vqα(k)為前級結構輸出的虛擬正交信號。

由式（3）～（5）得SDFT-QSG的z域傳遞函數為[16]

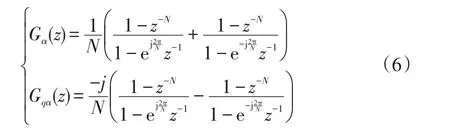
傳遞函數伯德圖如圖2所示。

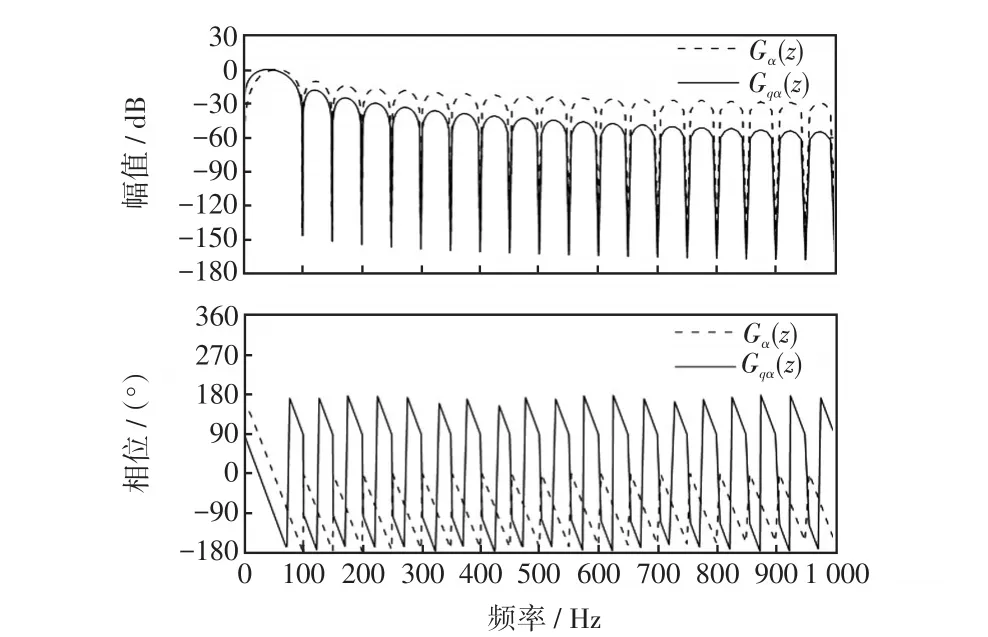
圖2 SDFT-QSG伯德圖Fig.2 Bode diagram of SDFT-QSG

由圖2可知：SDFT-QSG在指定頻率處，幅值增益衰減大，理論上可完全濾除畸變電網下多次諧波及直流偏移分量。

由文獻[15]可知，若SDFT采樣頻率非電網電壓基波頻率的N倍，系統將會發生頻譜泄漏，影響采樣精度，且SDFT-QSG提取的基波信號也會產生偏差，諧波與直流分量無法完全消除，系統會存在穩態誤差。

針對此問題，設計一種固定滑窗寬度-變滑窗寬度相結合機制的級聯型滑動窗離散傅立葉變換結構。

由圖2可知，vα(k)在基波頻率處與v(k)同相位，故以 vα(k)作為后級設計輸入端，其結構如圖3所示。

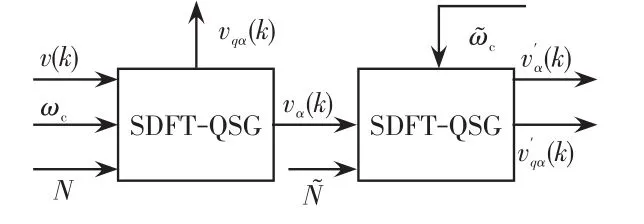
圖3 CSDFT-QSG結構Fig.3 Structure of CSDFT-QSG

2.2 后級頻率自適應設計

由式（3）可知，通過改變樣本周期點數N和系統的采樣周期Ts都可改變濾波器的窗口長度Tω，以達到后級SDFT-QSG頻率自適應。改變系統采樣周期，需每次周期迭代時，都依據電網電壓反饋的實時頻率更新采樣頻率 fs，數字處理器需要較大存儲空間，實現復雜。故此，采用更新樣本周期點數N，即

實際采集到的電網頻率通常不是整數，即使為整數，經式（7）運算，N也可能不為整數，需要進行取整運算，實現過程為

2.3 SDFT-QSG動態性能分析

經前文分析，前級SDFT采樣點數N取128，SDFT-QSG對諧波及直流偏移分量的抑制能力強。由文獻[15]可知，系統動態響應能力與樣本點數密切相關，樣本點數越大，系統動態響應速度越慢，這與鎖相環快速精準的鎖相能力相悖，故需要驗證SDFT結構動態性能。SOGI-QSG為常規正交信號發生器，具有較好的諧波抑制能力與動態響應能力，但對直流偏移分量抑制不佳。對SDFT與SOGI進行階躍響應對比，驗證SDFT的動態響應能力、抑制直流偏移能力。仿真結果如圖4所示。結果表明，SOGI-QSG的α與qα信號動態響應時間均優于SDFT，但SDFT也在一個基波周期20 ms達到穩態。SDFT-QSG的α與qα信號超調量較低，且穩態輸出為零，能夠較好地濾除直流偏移分量；而SOGIQSG的qα信號穩態輸出不為零，無法濾除直流偏移分量，其α與qα信號都存在穩態誤差。綜合考量，SDFT-QSG動態性能更優。

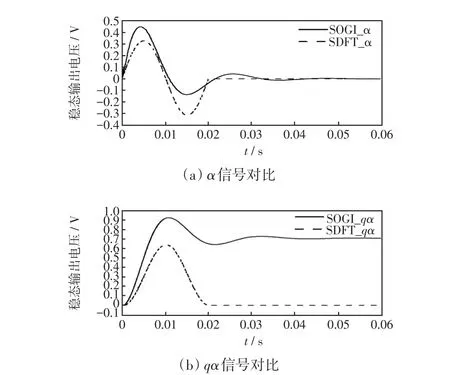
圖4 動態響應對比Fig.4 Comparison of dynamic response

3 MAF正、負序分量分離設計

不平衡電網電壓存在負序分量，將SDFT-QSG提取到的正交信號代入正、負序分量計算模塊PNSC（positive negative sequence calculator）原則上可消除負序分量，但電網畸變程度高將導致SDFT頻譜泄漏嚴重，PNSC交叉分解矩陣會導致相位檢測出現嚴重波動，影響頻率精度，故設計滑動平均濾波方法進行正、負序分離。

3.1 MAF原理分析

滑動平均濾波器MAF（moving average filter）的離散域傳遞函數為[11]

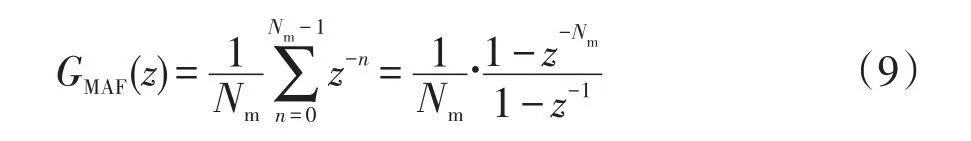
式中：Nm為MAF采樣點數（也稱濾波器階數），Nm=Tωmfsm，Tωm為MAF窗口寬度，其大小既影響濾波性能，又影響系統動態響應速度，Tωm越大，MAF濾波效果越好，但動態響應速度越慢；fsm為滑動平均濾波器采樣頻率。

取 Nm=100，fsm=10 kHz，則Tωm=0.01 s，相應的伯德圖如圖5所示。

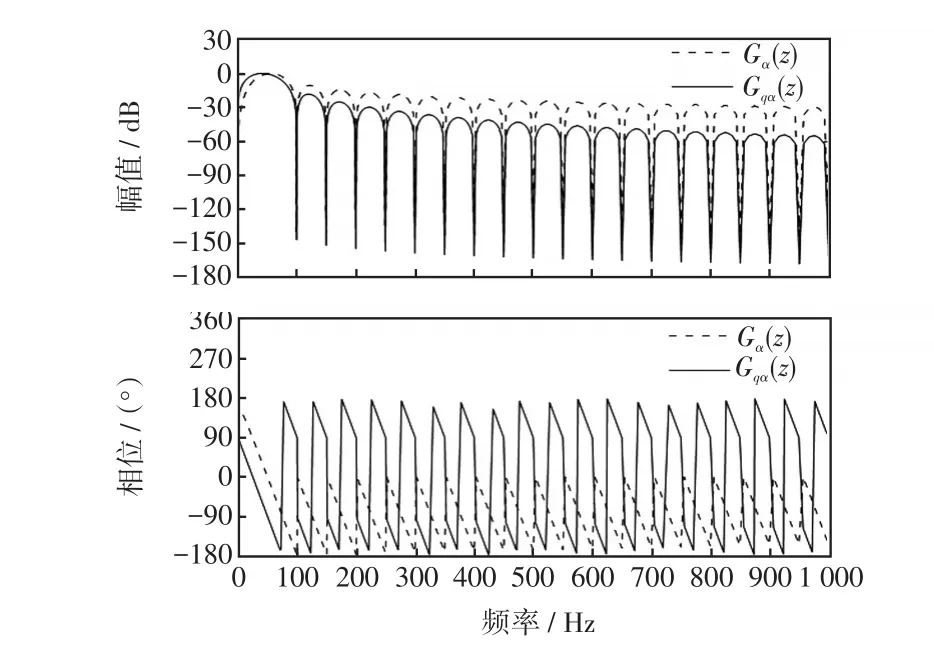
圖5 MAF伯德圖Fig.5 Bode diagram of MAF

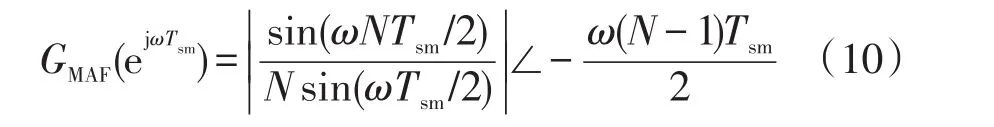
式中，Tsm為MAF采樣周期。

由式（10）及圖5可知，MAF可抑制特定頻次的諧波分量，但對直流分量無抑制作用。

3.2 電壓負序分量擾動分析

設αβ兩相靜止坐標系下的電壓表達式為

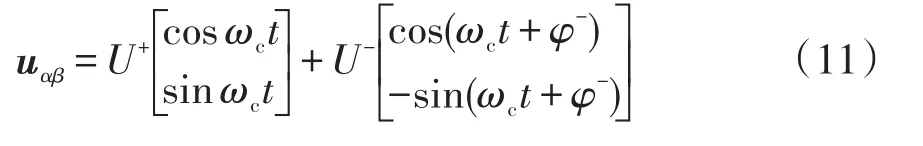
式中：U+、U-分別為正、負序基波電壓幅值；φ-為負序分量相對正序分量的初始相位角。

對式（11）進行Park變換，得dq兩相旋轉坐標系下的電壓表達式為

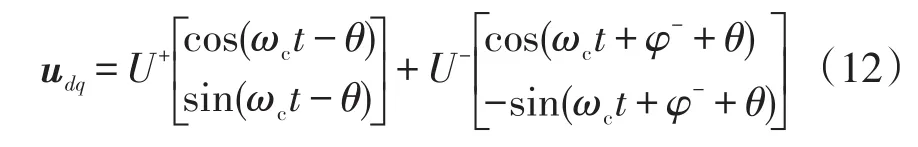
當鎖相環鎖定電網電壓正序分量旋轉位置時，即θ=ωct，式（12）改寫為

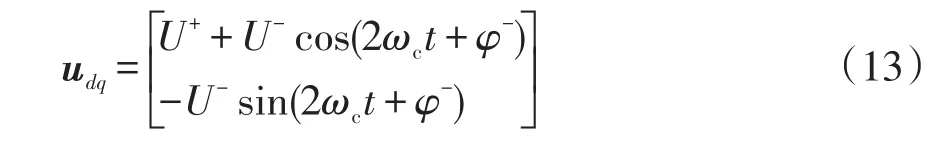
由式（13）可知：經坐標變換，正序分量轉化為直流分量，負序分量轉化為2倍頻分量。畸變電網下，負序分量對鎖相環產生較大擾動，使其無法準確檢測出正序分量相位信息。

3.3 負序分量消除設計

由上述分析，欲滿足精準鎖相的條件是：uq=0，而MAF對直流分量無抑制作用，故不會干擾系統判斷。負序分量通過坐標變換轉化為2倍頻分量，設計的核心是衰減100 Hz處頻率，由圖5可知，在100 Hz處，增益為-160 dB，滿足既定要求。

MAF負序分量消除原理如圖6所示。

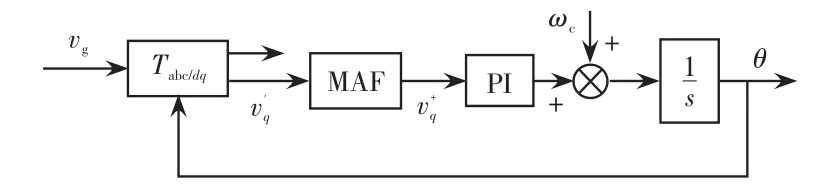
圖6 MAF負序分量消除結構Fig.6 Structure of MAF negative-sequence component elimination

圖6中，基于MAF負序分量消除具體步驟如下：

（1）通過坐標變換將abc三相靜止坐標轉換為dq兩相同步旋轉坐標；

（2）將輸出的q軸分量經過滑動平均濾波，濾除二倍頻分量；

（3）根據輸出的q軸信號進行SRF-PLL相位檢測控制，得到相角信息，并通過反饋環節為Park變換提供相位參考，通過PI控制調節，使直流分量為0，完成鎖相。

3.4 PI參數設計

建立電壓含擾動分量的小信號模型，如圖7所示。

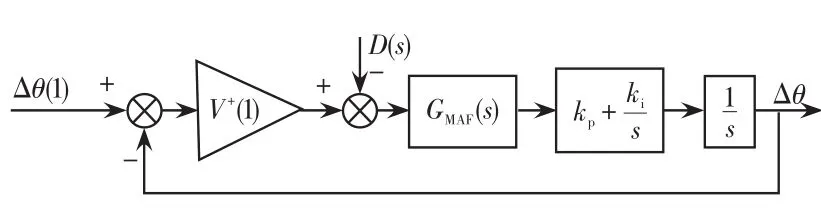
圖7 MAF-PLL小信號模型結構Fig.7 Structure of MAF-PLL small signal model

故 ξ＞1，根據參考文獻[17]，對鎖相環暫態過程與穩定性進行綜合考量，本文取ξ=2.4，kp=83.33，ki=2 893.5。

3.5 基于相位補償MAF動態性能設計

為提高MAF的動態性能，需對MAF引起的相位延遲進行補償。實現這一目標的簡單方法是在MAF控制回路中加入相位超前補償器[18]。

借鑒文獻[18]補償器的傳遞函數，設計MAF傳遞函數的逆函數，以有效補償MAF引起的相位延遲。傳遞函數為

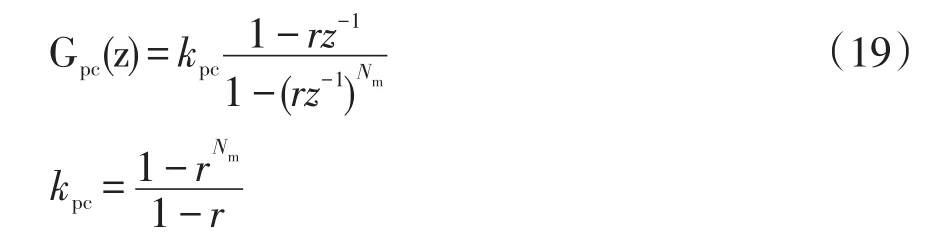
式中：kpc為傳遞函數幅值增益系數；r∈[0 1）為衰減因子。

帶有相位補償器的MAF，其衰減因子r取0.90、0.95、0.99的頻率響應如圖8所示。r為0時，系統傳遞函數不變，r為1時，相位補償控制器成為全通濾波器。結合MAF傳遞函數，權衡動態響應速度與濾除由負序分量引起的二倍頻振蕩，本文r取0.99，可有效補償由MAF引起的相位延遲。

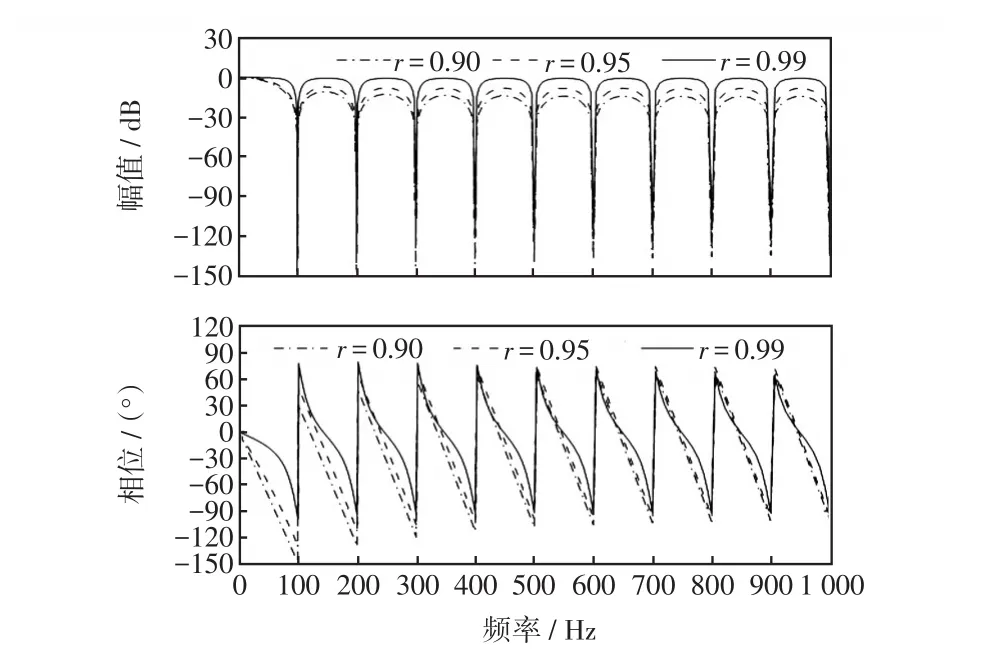
圖8 基于相位補償的MAF伯德圖Fig.8 Bode diagram of MAF based on phase compensation

由圖8可知，r=0.99系統動態特性更好。

綜上分析，設計的鎖相環結構如圖9所示。

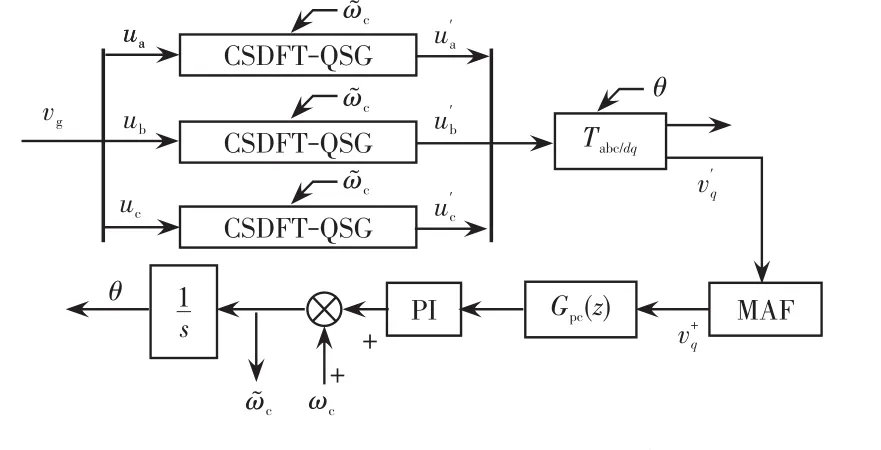
圖9 CSDFT-MAF-PLL結構Fig.9 Structure of CSDFT-MAF-PLL

4 仿真驗證與分析

為驗證所提方法正確性與可行性，在Matlab/Simulink中搭建仿真模型。將DSOGI-PLL、SDFTPLL和CSDFT-MAF-PLL進行對比分析驗證。為均衡DSOGI-PLL濾波性能和動態響應時間，阻尼系數設為0.707。CSDFT-QSG前級端N為128，采樣頻率fs為12.8 kHz。系統參數為：額定電壓有效值Vg為220 V，額定頻率為50 Hz，初始相位為0°。仿真工況設置為4種，如表1所示，具體故障類型設置為5種，如表2所示。

表1 仿真工況設計Tab.1 Design of simulation conditions

表2 故障類型設計Tab.2 Design of fault types

4.1 工況一

在1.4～1.6 s，進行工況一故障測試，仿真結果如圖10所示。

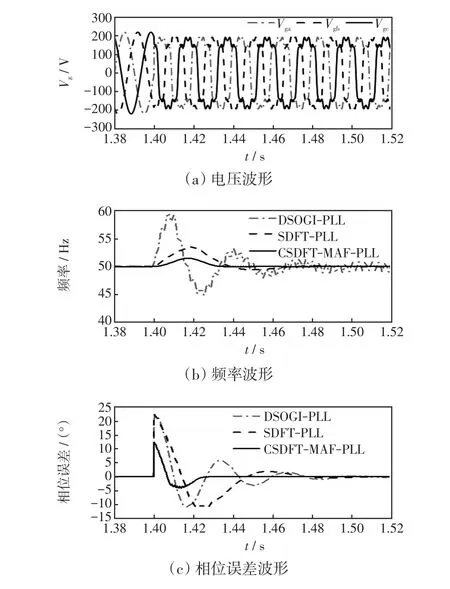
圖10 工況一仿真波形Fig.10 Simulation waveforms in Condition 1

由圖10可見：DSOGI-PLL頻率超調大，峰值為59.76 Hz，在既定時間內不能趨于穩定；SDFT-PLL超調了3.62 Hz；CSDFT-MAF-PLL超調量僅為1.5 Hz。SDFT-PLL相位誤差最大達22.5°，說明PNSC結構對SDFT有干擾。

4.2 工況二

在1.8～2.0 s，進行工況二故障測試，仿真結果如圖11所示。

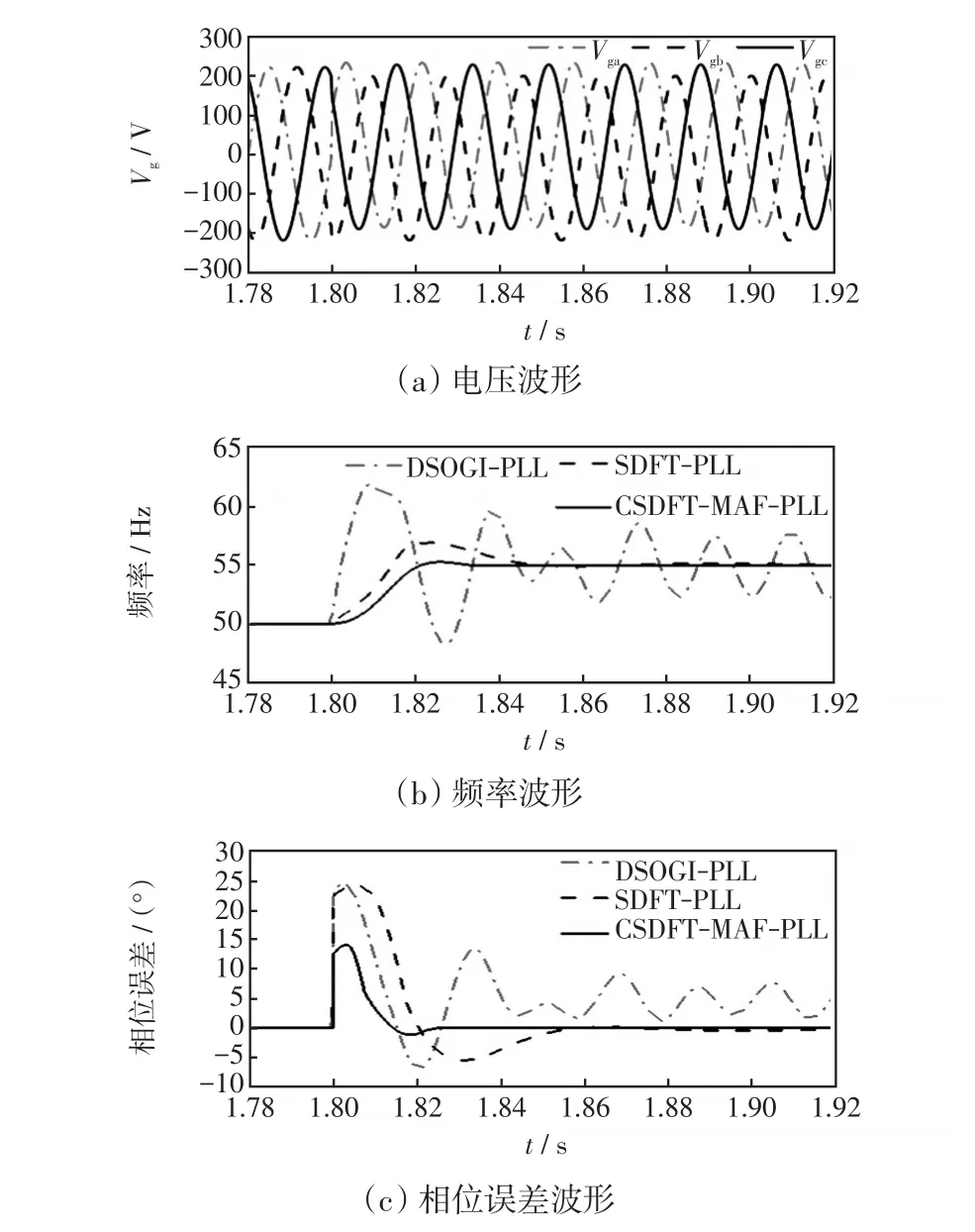
圖11 工況二仿真波形Fig.11 Simulation waveforms in Condition 2

由圖11可見：相較于工況一，DSOGI-PLL波動劇烈程度降低，但峰值增量提升，說明DSOGI結構對頻率跳變與直流偏移量敏感程度高；CSDFTMAF-PLL相位誤差最小達到-1°，比工況一提升約3.5°，故其對諧波注入較為敏感。

4.3 工況三

在2.2～2.4 s，進行工況三故障測試，仿真結果如圖12所示。

由圖12可見：DSOGI-PLL頻率動態峰值達到65 Hz，說明頻率跳變和多次諧波同時并存，對DSOGI模塊影響劇烈，而所設計的鎖相環超調量為0.27 Hz，并無明顯變化，說明所提策略魯棒性強。

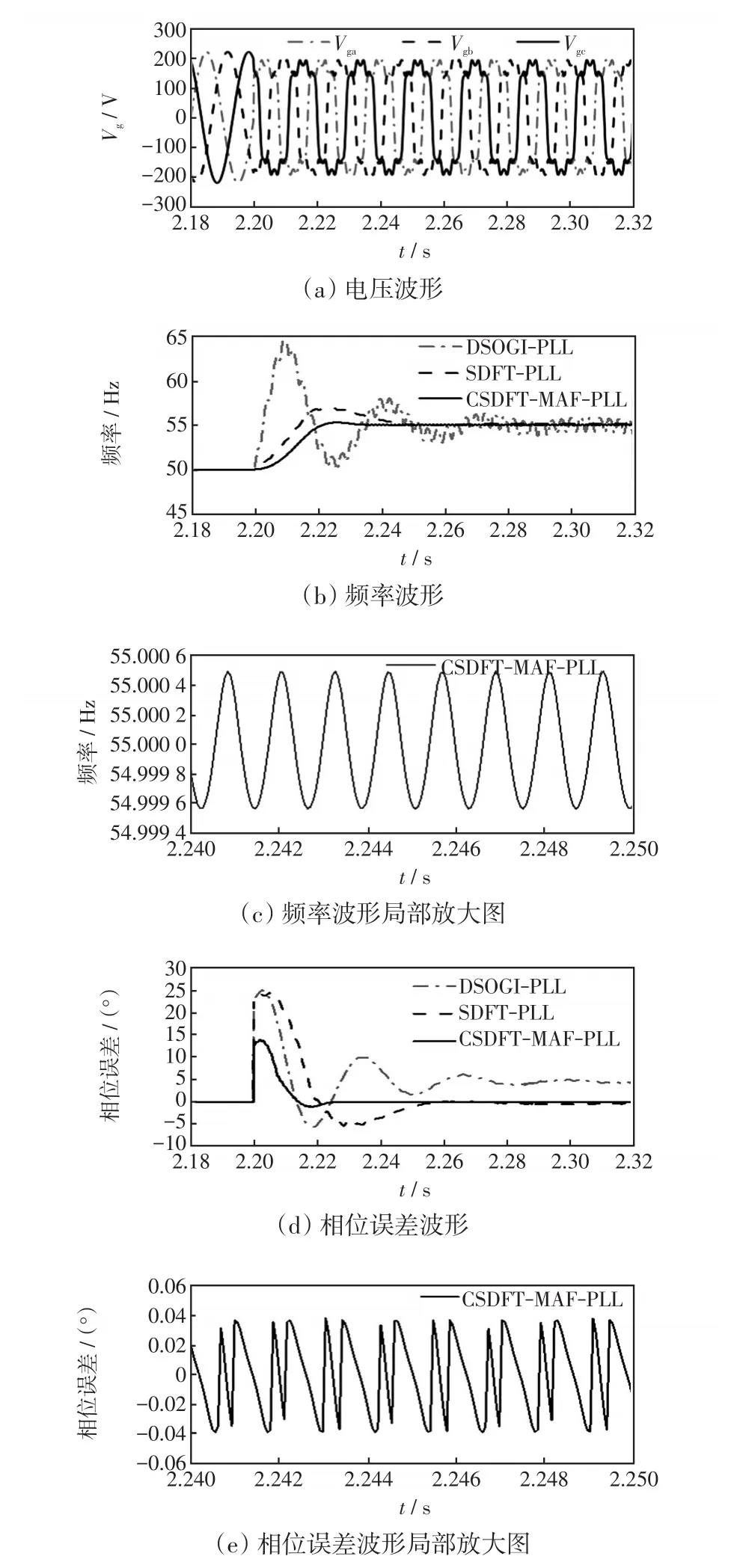
圖12 工況三仿真波形Fig.12 Simulation waveforms in Condition 3

4.4 工況四

在2.6～2.8 s，進行工況四故障測試，仿真結果如圖13所示。

由圖13可見，工況四最為復雜，相較于工況三，CSDFT-MAF-PLL穩態相位誤差約為0.059°，比工況三提高約0.02°，頻率變化不明顯。DSOGI-PLL頻率誤差大，且波動明顯。

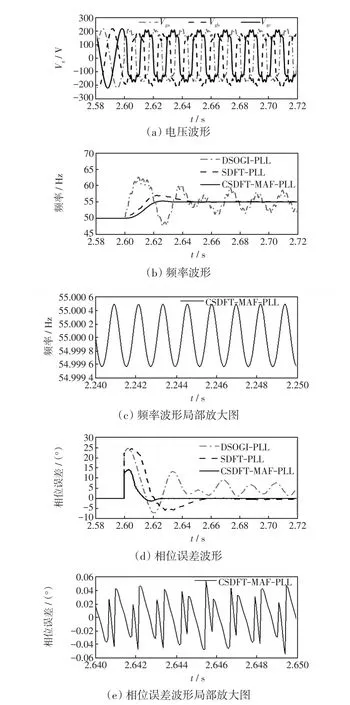
圖13 工況四仿真波形Fig.13 Simulation waveforms in Condition 4

綜上分析：數字濾波器采樣數據較大，SDFTPLL及CSDFT-MAF-PLL動態響應時間均滯后DSOGI-PLL，但在規定時限內；對比工況一、三，DSOGI-PLL相位穩態波動基本一致，但工況三下的相位誤差明顯高于工況一，可見DSOGI結構對頻率跳變很敏感，而設計的CSDFT結構降低了頻率跳變對頻譜泄漏的影響程度，相位誤差穩定在±0.04°；工況二、四與工況一、三對比，直流偏移使DSOGI-PLL頻率與相位誤差無法在額定百分比下達到穩態，而CSDFT結構波形光滑，穩態無誤差，諧波注入對其有一定影響，相位誤差增加，但在預期之內。綜合4種工況，都發生幅值與相位跳變，系統存在負序分量，而仿真結果表明所設計的MAF負序分量消除模塊效果顯著。CSDFT-MAF-PLL鎖相動態響應時間較快，并不因MAF的引入對系統造成很大延遲，說明所提相位補償控制器的有效性。相較于文獻[12]，穩態精度及動態響應速度均有明顯改善。

5 結論

針對SDFT-PLL在復雜電網條件下鎖相優勢與不足展開研究，結合MAF優良濾波性能，設計CSDFT-MAF-PLL。理論分析與仿真驗證得出以下結論：

（1）提出CSDFT-QSG結構，顯著提升系統諧波抑制與直流偏移消除能力，并對頻率、幅值、相位跳變不敏感，以電網實時頻率作為后級SDFT滑窗寬度選取依據，從而減小SDFT因頻譜泄漏導致的頻率穩態誤差；

（2）提出MAF負序分量消除設計，將三相電網電壓的正序分量送入SRF-PLL，負序分量轉化為二倍頻分量被抑制；

（3）提出相位補償控制器，克服MAF相位延遲的弊端，使所設計的鎖相環在各種工況下，達到穩態的時間均保持在1.5個基波周期左右。

本文建立單機無窮大電網系統，進行了4種工況下鎖相并網性能研究，模型結構相對單一。下一步研究可以結合雙饋風電系統，開展鎖相環動態特性對系統慣性響應及穩定性分析。