應用新型能量函數的PWM整流器無源性控制方法

袁 敞，戴篤猛，邱俊卿

（新能源電力系統國家重點實驗室（華北電力大學），北京 102206）

電力電子換流器在電力系統中的廣泛應用對電力系統的運行方式及動態特性造成了影響，并給電力系統的穩定性帶來了嚴峻的挑戰[1-4]。由于傳統的電力電子換流器線性控制需在系統的穩態工作點附近進行線性化，僅適用于系統參數變化和擾動較小的情況，因此，該類控制策略只能保證局部穩定性[5]。

1989年，Ortega等[6]首次提出了無源性控制的思想。無源性控制能夠實現系統的全局穩定性，無奇異點問題，對系統參數變化及外來擾動均具有較強的魯棒性，是一種本質上的非線性控制方法。自提出以來，無源性控制在機械系統、電機控制與電力系統中便得到了廣泛應用。1990年，Lozano等[7]首先將無源性控制應用于機械手的控制中，此后，該控制在機器人領域得到迅速發展[8-9]。1997年，Gokdere等[10]提出了一種感應電機的無源性控制方法，簡化了系統的控制結構，提高了系統的穩定性和魯棒性。2000年，Carrasco等[11]將無源性的思想應用在電力電子換流器領域，改善了直流-直流串聯諧振換流器的輸出電壓調節問題；2001年，Valderrama等[12]利用無源性控制策略解決了靜止同步補償器STATCOM（static synchronous compensator）中不平衡電流的調節問題；隨著無源性理論的不斷成熟，無源性控制迅速在電力電子換流器領域得到廣泛應用并取得不錯的控制效果[13-17]。

無源性控制作為一種本質穩定的控制方法，滿足了系統的穩定性要求，但其動態響應的快速性尚需優化。為提高無源性控制的快速性，文獻[18]改變了傳統無源控制中的固定阻尼注入方式，在起始階段注入大阻尼，接近穩態時注入小阻尼來實現狀態變量的快速跟蹤，文獻[19-20]通過注入虛擬阻尼與添加比例-積分調節器的方法，實現了對系統狀態的快速跟蹤。目前，絕大多數改善無源性控制的方法均為調節阻尼系數，較大的阻尼系數可以加快狀態變量收斂到穩態值的速度，但是會引起動態過程較為劇烈地振蕩，在快速性和穩定性之間仍存在一定的矛盾。

針對三相脈沖寬度調制PWM（pulse width modulation）整流器在直流側電壓參考值突變時無源性控制無法使直流側電壓快速跟蹤其參考值的現象，本文首先推導PWM整流器在旋轉坐標系下的數學模型，基于該模型對整流器進行歐拉-拉格朗日建模并構建相應的無源性控制器，從誤差能量存儲函數的角度分析產生該現象的原因，進而提出一種基于新型能量函數的PWM整流器的無源性控制方法。該方法在加快直流側電壓跟蹤速度的同時保持了穩態三相電流具有良好的波形質量。仿真驗證了所提控制方法的有效性。

1 基于新型能量函數的無源性控制方法

1.1 三相PWM整流器的數學模型

三相三線制PWM整流器的拓撲結構如圖1所示。

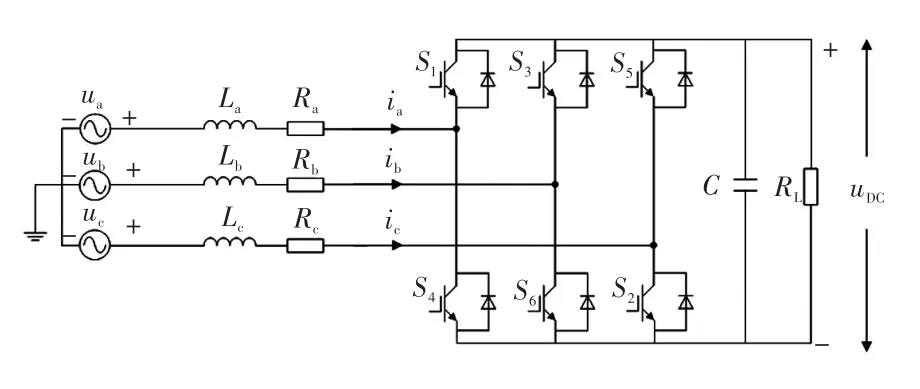
圖1 三相三線制PWM整流器的拓撲結構Fig.1 Topology of three-phase three-wire PWM rectifier

定義 Si（i=a，b，c）為絕緣柵雙極型晶體管IGBT（insulated gate bipolar transistor）的開關函數，Si為1表示上橋臂導通，下橋臂關斷；Si為0表示上橋臂關斷，下橋臂導通；令交流側三相電感均為L，電阻均為R，根據基爾霍夫定律，其等效數學模型為

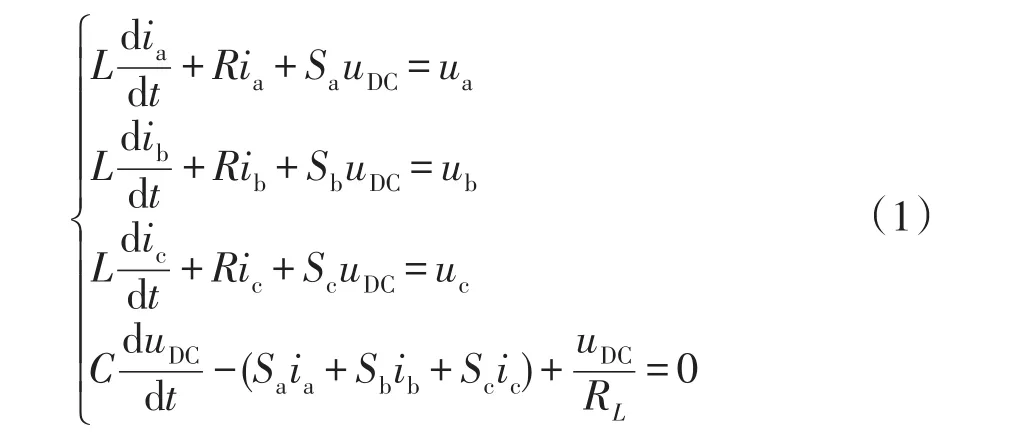
式中：ui(i=a,b,c)、ii(i=a,b,c)分別為交流側三相電源電壓及電流；C為直流側電容；L為每相橋臂的等效電感；R為每相橋臂的等效電阻；uDC、RL分別為直流側電壓及負載電阻。

利用派克變換，將三相靜止坐標系下的數學模型轉換為兩相旋轉坐標系下的數學模型：

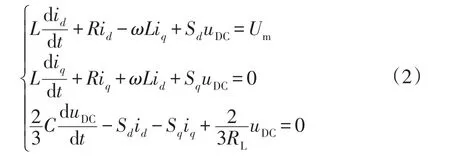
式中：Um為相電壓幅值，即交流側三相電源電壓在d軸的分量；ω為電角速度；id、iq分別為ii(i=a,b,c)在兩相旋轉坐標系下的對應值；Sd、Sq分別為開關函數Si(i=a,b,c)在兩相旋轉坐標系下的對應值。

1.2 無源性控制理論及EL系統

無源性控制理論的總出發點為系統的能量，其核心思想是只要一個系統的能量得到控制，其內部各參數也相應地得到控制[21]。它構造與被控物理量相關的能量存儲函數，基于此設計系統的無源性控制器，通過對能量進行控制來達到對目標物理量的控制。該控制可實現系統的全局穩定，無奇異點問題，是一種本質穩定的非線性控制方法。

歐拉-拉格朗日EL（Euler-Lagrange）系統是一類可以用歐拉-拉格朗日方程來描述的系統，歐拉-拉格朗日方程的一般數學表達形式如式（3）所示。式中：M為正定慣性矩陣，J為反對稱矩陣，R為正定耗散矩陣，r表示外界與系統之間的能量交換，x為選定的狀態變量。在實際工程中，有大量的系統可以用歐拉-拉格朗日方程來描述，且這些系統內部不含能量源，則可以利用歐拉-拉格朗日方程和系統的無源性來設計其非線性控制器。

若將阻尼的作用考慮在內，EL方程可改寫為

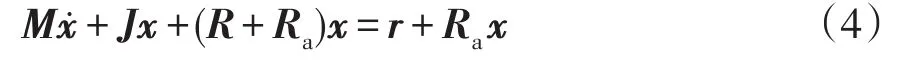
式中，Ra為注入的阻尼矩陣。

1.3 PWM整流器的傳統無源性控制器設計

三相PWM整流器在兩相旋轉坐標系的數學模型可用式（3）來描述，其中：

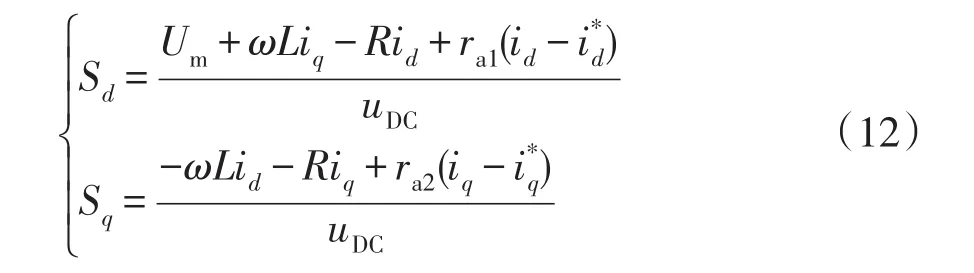
式中，ra1、ra2分別為d、q軸對應的阻尼系數。

1.4 新型能量函數

從誤差能量函數的導數表達式（11）可以看出，誤差能量函數的收斂速度與狀態變量和其穩態值之間的誤差xe有直接關系，隨著各狀態變量逐漸趨向于其穩態平衡點，xe也逐漸趨向于0，進而導致誤差能量函數的收斂速度H˙e(x)越來越小，系統趨向于其穩態平衡點的速度也越來越慢。對于能量函數H(x)的要求如下。

（1）?x,H(x)≥0恒成立。

（2）x=0為 H(x)的嚴格最小值點，即?x≠0,H(x)≥H(0)恒成立。

為消除誤差能量函數的收斂速度與狀態變量誤差xe之間的強相關關系，本文重新定義系統的能量函數為

恒成立，所以該系統嚴格無源。

1.5 應用新型能量函數的無源性控制器設計

為滿足誤差能量儲存函數的導數恒小于等于0，只需令

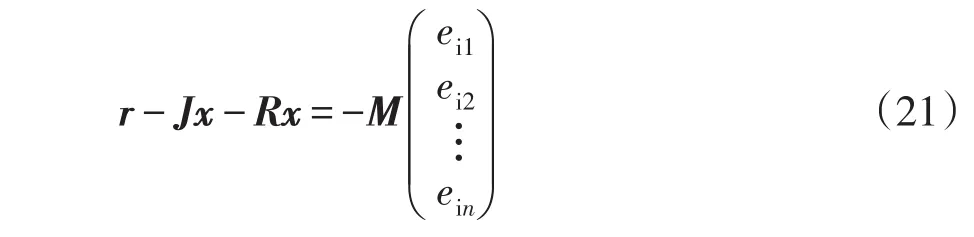
該式中，列向量中各項的正負號與式（18）中行向量各位置一致。

為加速誤差能量函數的收斂，考慮注入阻尼，即令

基于新型能量函數的無源性控制系統示意圖如圖2所示。

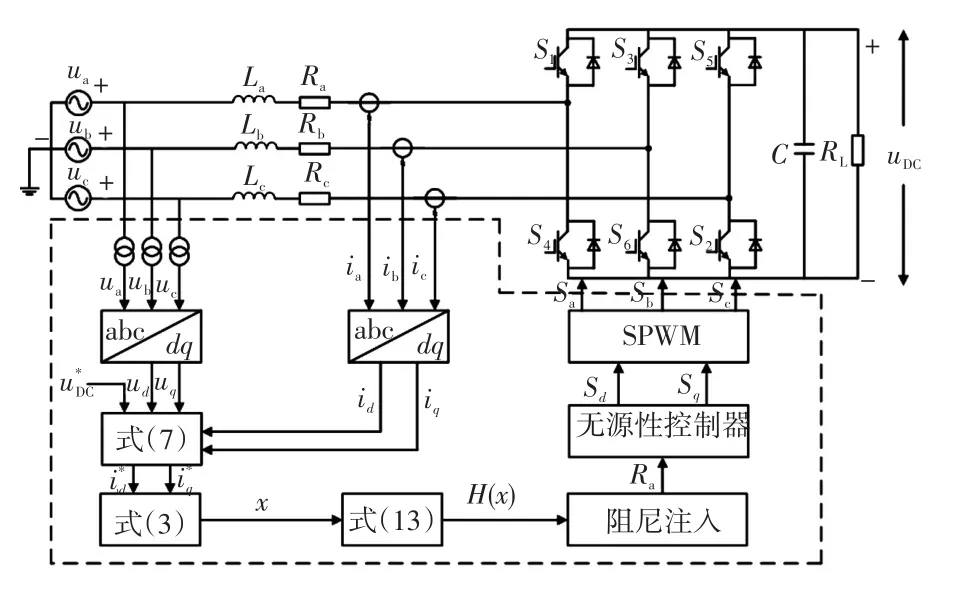
圖2 基于新型能量函數的無源性控制系統示意Fig.2 Schematic of passivity-based control system based on novel energy function

2 仿真驗證

仿真參數設計如表1所示[22]。

表1 仿真參數設置Tab.1 Setting of simulation parameters

仿真以直流側電壓參考值在0.1 s時由600 V突變至700 V為例，綜合對比了傳統無源性控制與應用新型能量函數的無源性控制兩種控制方法電壓的跟蹤情況，仿真結果如圖3所示。

圖3 直流側電壓對比Fig.3 Comparison of DC-side voltage

綜合對比2種不同的無源性控制的仿真結果可以發現，在0.1 s時從600 V階躍至700 V時，基于新型能量函數的無源性控制僅用時0.024 s就使得直流側電壓跟蹤上；傳統無源性控制需用時0.44 s才使直流側電壓跟蹤上，前者的速度為后者的18倍。

應用新型能量函數的無源性控制和傳統無源性控制的a相電流仿真結果對比如圖4所示。由圖4可以發現，0.1 s時直流側電壓參考值突變，傳統無源性控制的電流需要歷經一個較長的過程才能到達最后的穩定狀態，歷時為0.44 s；而應用新型能量函數的無源性控制僅用時0.024 s就可以使電流到達最后的穩定狀態；應用新型能量函數的電流在動態過程中的波動較傳統無源性控制大一些。到達穩定狀態之后，兩種控制方法的電流均具有良好的波形質量。

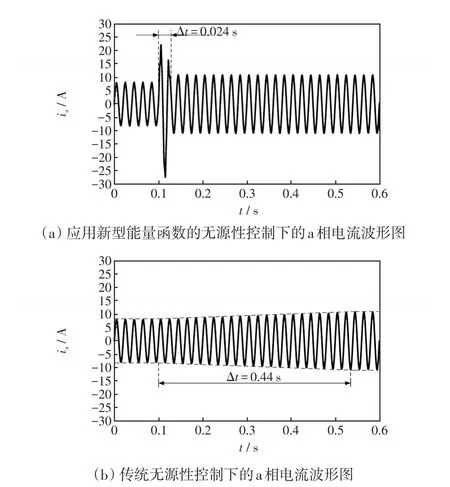
圖4 電流仿真結果對比Fig.4 Comparison of current simulation results

0.1 s時直流側負載RL由100 Ω突變至50 Ω，應用新型能量函數的無源性控制的直流側電壓和電流的仿真結果如圖5所示，從仿真結果中可以看到，0.1 s時負載突變至原來的50%，直流側電壓因此產生的穩態誤差不超過2 V，誤差量在0.3%之內，直流側電流也可迅速過渡到新的穩定狀態。

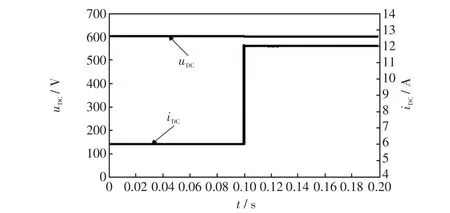
圖5 負載突變時的直流側電壓電流仿真Fig.5 Simulation of DC-side voltage and current when load changes suddenly

交流側三相電源電壓的有效值由380 V突變至300 V時直流側電壓電流的仿真結果如圖6所示，從仿真中可以看到，在0.1 s時電源電壓突變，直流側電壓因電壓突變產生的穩態誤差不超過0.3 V，誤差量在0.05%之內；直流測電流的穩態誤差不超過0.004 A，誤差量在0.067%之內。

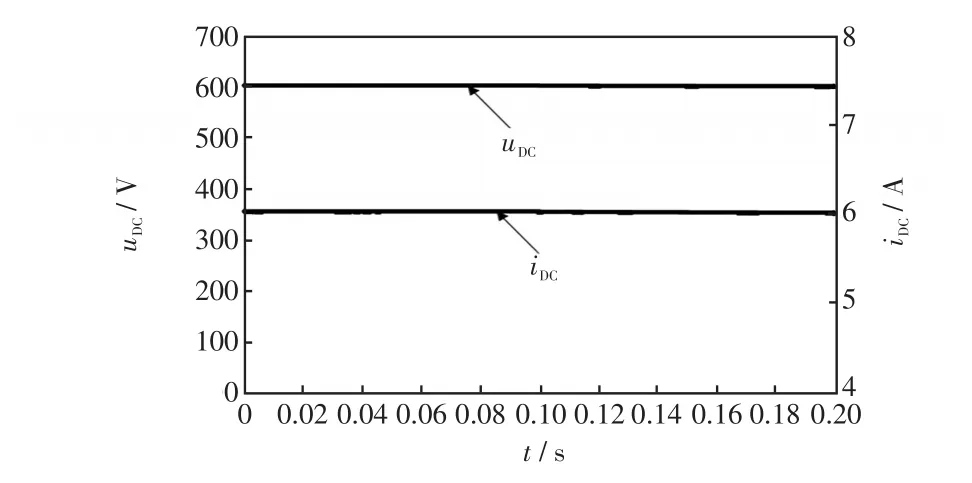
圖6 三相電源電壓突變時直流側電壓電流仿真Fig.6 Simulation of DC-side voltage and current when three-phase power supply voltage changes suddenly

綜合分析圖5和圖6可以發現，應用新型能量函數的無源性控制在外界條件發生突變時仍然可以將直流側的電壓和電流維持在參考值附近，波動量很小，這說明應用新型能量函數的無源性控制具有較強的抵抗外界參數擾動的能力。

3 結論

針對應用傳統無源性控制的PWM整流器在直流側電壓參考值突變時直流側電壓跟蹤速度較慢的問題，本文從能量函數的角度入手，分析了造成該現象的原因是狀態變量的誤差逐漸變小導致誤差能量函數的收斂速度越來越慢。為解決該問題，本文提出了一種應用新型能量函數的無源性控制方法，結論如下：

（1）在PWM整流器直流側參考電壓突變時，相比于傳統無源性控制，應用新型能量函數的無源性控制可以顯著提高直流側電壓的跟蹤速度；

（2）應用新型能量函數的無源性控制的三相電流具有良好的波形質量；

（3）應用新型能量函數的無源性控制具有較強的抗外界參數擾動的能力；

（4）仿真驗證了所提策略的有效性。