側滑打滑時的WMR抗飽和模糊超螺旋滑模控制

李振陽，董方明，佃松宜，趙 濤

(四川大學電氣工程學院，四川 成都 610065)

1 引言

輪式移動機器人(Wheeled Mobile Robot，WMR)廣泛應用于工業制造、航空航天以及服務業中，而軌跡跟蹤控制是WMR的核心控制問題，吸引了大量學者進行相關方法的研究。目前，針對WMR的軌跡跟蹤控制方法，主要有反演控制[1]、自適應控制[2]、模糊控制[3]、神經網絡控制[4]以及滑模控制[5]。上述文獻提出的方法，均假設WMR滿足理想的純滾動非完整約束。但在實際應用中，當WMR在濕滑地面運動或者急速轉彎時，可能出現側滑和縱向打滑現象，破壞理想非完整約束。

目前，針對理想非完整約束的WMR軌跡跟蹤問題已經有大量的研究成果，然而針對具有側滑、縱向打滑干擾下的WMR軌跡跟蹤問題的研究還較少。文獻[6]考慮WMR輪子的縱向打滑，設計了基于滑模觀測器的運動學軌跡跟蹤控制器，但其僅在運動學層面進行控制律設計，忽略了WMR的動力學屬性。文獻[7]提出一種基于廣義擴張狀態觀測器的魯棒控制方法，但其需要系統擾動的上界信息。文獻[8]設計一種模糊干擾觀測器，對WMR的側滑和打滑干擾進行觀測，但該方法對外界不確定擾動考慮不足。文獻[9]采用神經網絡對側滑和打滑干擾進行逼近，結合強化學習機制實現軌跡跟蹤控制，但該控制器設計復雜，難以用于實時控制。文獻[10-11]提出一種基于自抗擾思想的動力學控制器，通過線性擴張狀態觀測器對WMR系統總體不確定性進行估計，但其軌跡跟蹤初期具有較大的力矩跳變，對執行器的損害較大。

上述文獻在理想非完整約束的基礎上，進一步研究了WMR的側滑、打滑干擾，但均未考慮WMR執行器的飽和約束問題。而在實際控制過程中，執行器的飽和約束是不可忽略的。如果設計的控制器輸出量大于執行器能夠承受的上界值，則容易造成執行器的損壞，導致整個控制系統失效[12]。綜合上述分析，本文設計一種抗飽和模糊超螺旋滑模控制方法，相較于文獻[6]-[11]，所提出的控制方法不僅考慮了WMR軌跡跟蹤過程中未知上界的側滑打滑干擾和外界擾動，同時能夠處理WMR的執行器飽和約束問題。

本文的貢獻及創新點主要有：1)建立具有側滑打滑干擾以及執行器飽和約束的WMR模型，相較已有的研究，更貼近實際應用；2)設計具有飽和約束系統的WMR動力學控制器，實現WMR在執行器飽和約束條件下的抗飽和控制；3)設計超螺旋滑模控制律，減小系統控制力矩中的抖振現象，并設計模糊系統對超螺旋控制律中的參數進行在線自適應調整，增強控制器在WMR系統擾動上界未知時的抗擾能力。

2 模型分析

圖1為包含側滑、打滑干擾時的WMR示意圖。其中X-O-Y為全局坐標系，XC-C-YC為WMR的局部坐標系，b為輪子與質心之間的距離，r為輪子的半徑，C為WMR的質心，v和ω分別為線速度和角速度，vyc為側滑速度，ξr和ξl為輪子縱向打滑角速度擾動。

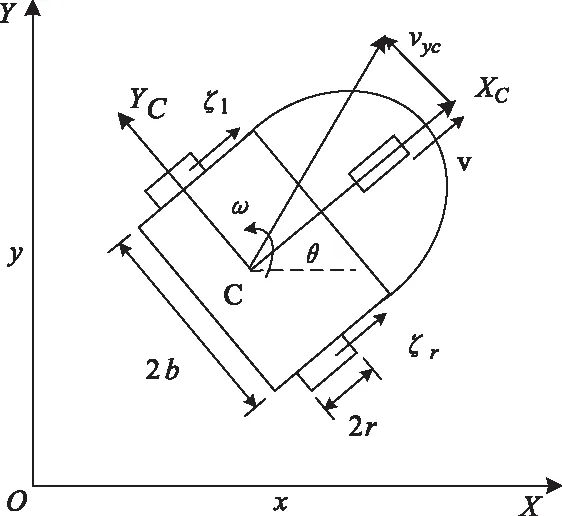
圖1 WMR示意圖

設WMR在坐標系X-O-Y中的位姿向量為q=[x，y，θ，θr，θl]T，存在側滑、縱向打滑時的非完整約束方程為

(1)

其中(x，y)為質心C在坐標系X-O-Y中的坐標，θ為轉向角，θr和θl為驅動輪轉動角度。

簡化式(1)，非完整約束方程可以表示為

(2)

其中

Λ=[vyc，-rξr，-rξl]T.

定義矩陣S(q)如下，其滿足A(q)S(q)=0。

(3)

由式(2)和(3)，得到側滑、縱向打滑時的WMR運動學方程

(4)

其中

z=[v，ω]T，ζ=[ζv，ζw]T

其中z=[v，ω]T為WMR的線速度和角速度，ζv和ζω為縱向打滑擾動，ψ(q，vyc)為側向滑動造成的干擾。由文獻[11]可知，干擾ζv，ζω，ψ(q，vyc)均有界，并且其一階導數也有界。

根據拉格朗日動力學方程，WMR動力學模型可以表示為

(5)

其中M(q)∈5×5為慣性矩陣，5×5為科氏矩陣，G(q)∈5×1為重力項，B(q)∈5×2為變換矩陣，τ∈2×1為力矩項，η為拉格朗日算子。

對式(3)求導，代入式(5)，左乘S(q)T，考慮模型不確定性和外界干擾，則動力學模型為

(6)

其中

m=mc+2mw，I=Ic+2Im+2mwb2

其中mc、mw、Ic、Im、Iw為WMR相關物理參數。D為系統總擾動，與側滑打滑干擾、外界擾動和模型不確定性有關，具體形式為：

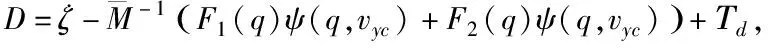
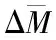
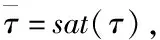
(7)

飽和約束函數為

(8)

則考慮執行器飽和約束條件時，式(6)所示的動力學模型可以改寫為

(9)

3 控制器設計

為降低整個WMR系統控制器的設計復雜度，本文采用反演法設計WMR軌跡跟蹤控制器，即把WMR分為運動學和動力學兩個子系統，分別設計運動學輔助控制器和動力學控制器。

3.1 運動學輔助控制器設計

根據WMR的運動學模型(4)可知，WMR可以通過線速度和角速度調整，實現軌跡調整，因此運動學控制器需輸出合適的速度控制律，使軌跡跟蹤誤差收斂于零。首先設WMR在坐標系X-O-Y中跟蹤的參考軌跡qr=[xr，yr，θr]T為

(10)

其中vr、ωr分別為參考線速度和角速度，且有vr>0.

結合WMR的實際軌跡q和參考軌跡qr，可以推導出軌跡跟蹤誤差qe為：

(11)

對式(11)求導可得qe的動態方程

(12)

根據qe的動態方程，設計WMR的運動學輔助控制器[1]

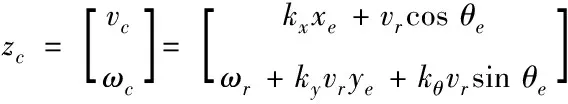
(13)

式(13)中，kx>0、ky>0、kθ>0為WMR運動學輔助控制器參數。vc和ωc分別為運動學輔助控制器得到的虛擬線速度和角速度。

3.2 動力學控制器設計

根據WMR的動力學模型式(9)，本文設計的WMR動力學控制器，以運動學控制器的輸出zc作為參考輸入，得到力矩控制輸出，實現WMR的速度跟蹤。動力學控制器的設計步驟為：1)抗飽和輔助系統設計；2)抗飽和超螺旋滑模動力學控制器設計；3)抗飽和模糊超螺旋滑模動力學控制器設計。

3.2.1 抗飽和輔助系統設計

根據式(7)-(9)可知，WMR的執行器存在飽和約束，執行器輸出不能超過最大輸出值τmax，因此需要設計抗飽和輔助系統，實現WMR的執行器飽和補償。抗飽和輔助系統設計如下

(14)

式(14)中，λ=[λ1，λ2]T為輔助系統的狀態變量，H為式(9)中的參數矩陣，Δτ為式(7)所示的飽和約束誤差，矩陣A為

為保證WMR的抗飽和輔助系統(14)穩定，矩陣A需滿足Hurwitz條件，即a1>0，a2>0[12].

3.2.2 抗飽和超螺旋滑模動力學控制器設計

根據WMR運動學輔助控制器輸出zc和抗飽和輔助系統狀態變量λ，定義WMR的速度跟蹤誤差ze

(15)

其中v和ω分別為WMR的實際線速度和角速度。根據WMR速度跟蹤誤差ze，構建積分滑模面

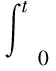
(16)

其中β>0為滑模面參數。為了設計WMR動力學控制器中的滑模控制律，需推導滑模面的導數，結合式(7)、式(9)、式(14)和式(15)，有

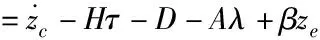
WMR的滑模動力學控制律分為等效控制律和切換控制律，設計如下

1)等效控制律

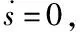
(18)

2)切換控制律

等效控制律τeq能在不考慮WMR系統總擾動的條件下，使系統狀態保持在滑模面上。但WMR系統的總擾動不可忽略，需要引入切換控制律，補償系統總擾動D.為了克服傳統滑模控制中廣泛存在的抖振現象，采用超螺旋滑模控制律[13]作為WMR的切換控制律

(19)

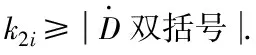
結合τeq和τsw，得到WMR的抗飽和超螺旋滑模動力學控制器

(20)

3.2.3 抗飽和模糊自適應超螺旋動力學控制器設計

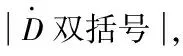
為解決控制器(20)在D未知時參數選擇困難的問題，設計模糊系統，估計WMR超螺旋滑模控制律的參數K1和K2.以用于1估計的模糊系統為例，具體設計步驟為：

1)WMR滑模面模糊化

以式(16)構建的WMR滑模面si作為模糊系統的輸入，通過如下的模糊規則進行模糊化處理

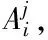
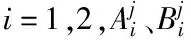
2)解模糊輸出控制器參數

采用權值平均法解模糊，得到模糊系統的清晰化輸出，即WMR超螺旋控制律的參數k1i：

(21)

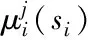
通過上述模糊系統對WMR超螺旋滑模控制律中的控制參數進行估計，設1和2分別為模糊系統對WMR超螺旋滑模動力學控制器參數的估計值，表達式如下

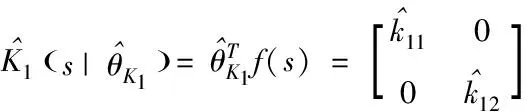
(22)

(23)

由此可在式(20)的基礎上，進一步得到WMR的抗飽和模糊超螺旋滑模動力學控制器

(24)

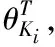
(25)

(26)

式中：αi>0和βi>0為學習率參數。結合WMR的運動學輔助控制器，整個控制框圖如圖2所示。

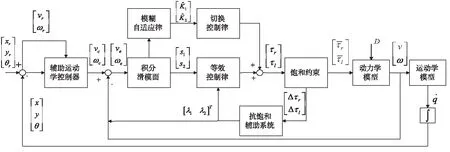
圖2 控制系統框圖

4 穩定性分析

本節基于Lyapunov穩定性理論，對設計的WMR軌跡跟蹤控制器進行穩定性分析。

定理：采用運動學輔助控制律式(13)、抗飽和模糊超螺旋滑模控制律式(24)和模糊超螺旋自適應律式(25)～(26)，可以保證WMR的軌跡跟蹤誤差qe和速度跟蹤誤差ze漸進穩定。

證明：設計Lyapunov函數為

V=V1+V2

(27)

其中V1用于分析WMR運動學控制器式(13)的穩定性，V2用于分析WMR動力學控制器式(24)的穩定性，具體表達式為

(28)

(29)

1)WMR運動學控制器穩定性分析

V1對時間求導，將式(12)～(13)代入，則

(30)

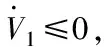
2)WMR動力學控制器穩定性分析

V2對時間求導，將式(22)～(24)代入，有

(31)

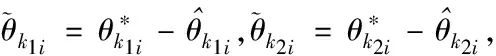
將式設計的模糊系統參數自適應律(25)、(26)代入式(31)中，可以得到

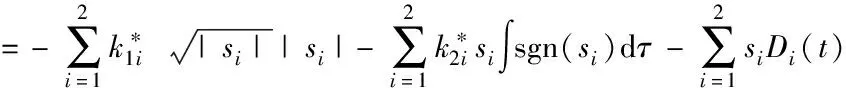
≤0.

(32)

綜上，設計的控制系統可以保證WMR的軌跡跟蹤誤差qe和速度跟蹤誤差ze漸進穩定。證畢。

5 仿真研究

為驗證本文所提出控制方法的有效性，通過Matlab進行仿真研究。WMR模型參數為

mc=2kg，mw=0.5kg，b=0.15m，r=0.05m，Ic=0.0675kg·m2，Im=0.0125kg·m2，Iw=0.01125kg·m2.

運動學輔助控制器參數為：kx=8，ky=10，kθ=10.模糊系統采用三個三角隸屬度函數，如圖3所示。滑模面參數為β=7，模糊自適應律學習率參數為：α1=15，α2=5，β1=80，β2=100.模糊系統的參數向量k1i、k2i初始值取0.01.抗飽和輔助系統的參數取a1=a2=10，λ1和λ2的初始值取0.01.執行器的飽和約束取τmax=8N·m.

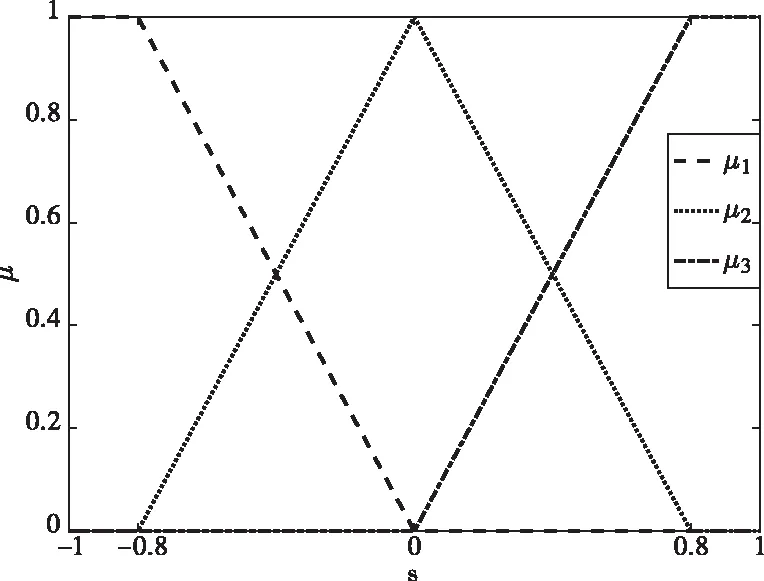
圖3 三角隸屬度函數

參考速度取vr=1m/s，ωr=0.5rad/s，初始位姿取qr=[1.2，0.8，0]T；實際初始位姿為取q=[0，0，0]T，初始速度取v=0m/s，ω=0rad/s.

為了驗證所提出的模糊超螺旋滑模控制方法不需要系統擾動的上界信息，在仿真中加入不同上界值的擾動：當t<15s時，不考慮側滑和打滑，僅取：Τd=[Td1，Td2]T=[2sin(t)，2sin(t)]T.

當t≥15s時，加入側滑和打滑，取橫向滑移速度為vyc=1m/s，縱向打滑角速度擾動取為：ξr=sin(t)、ξl=sin(2t)+0.5.并且取較大的擾動：Τd=[Td1，Td2]T=[12sin(t)，15sin(t)]T.

與固定增益的等速趨近律滑模控制器和超螺旋滑模控制器進行對比。固定增益等速滑模控制器參數選取Γ=diag{5，5}，固定增益超螺旋控制器參數選取為：K1=diag{5，5}，K2=diag{5，5}.

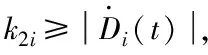
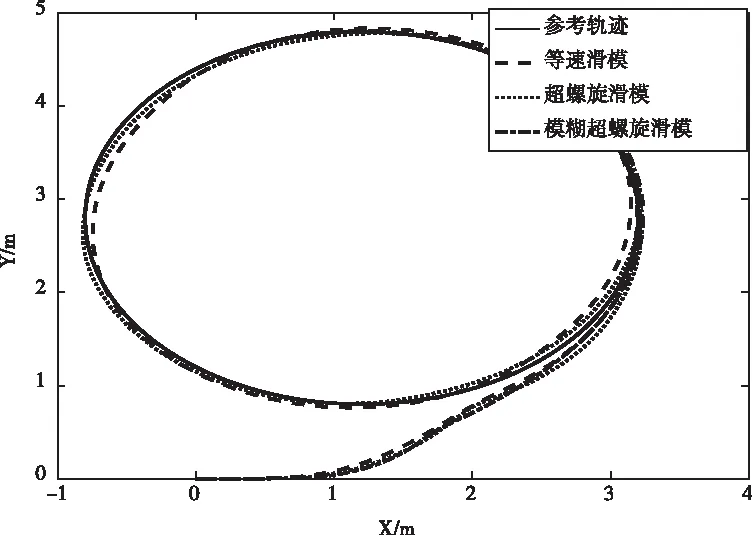
圖4 軌跡跟蹤曲線

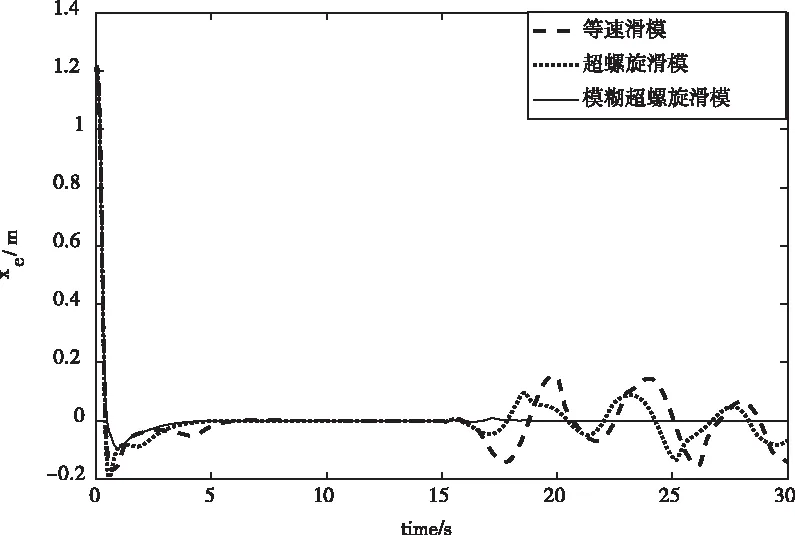
圖5 X軸誤差

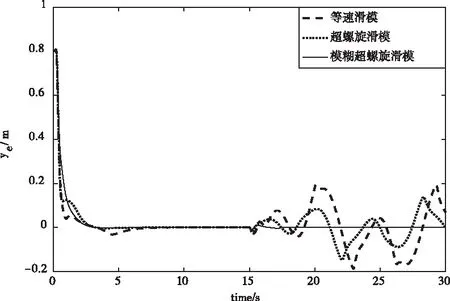
圖6 Y軸誤差

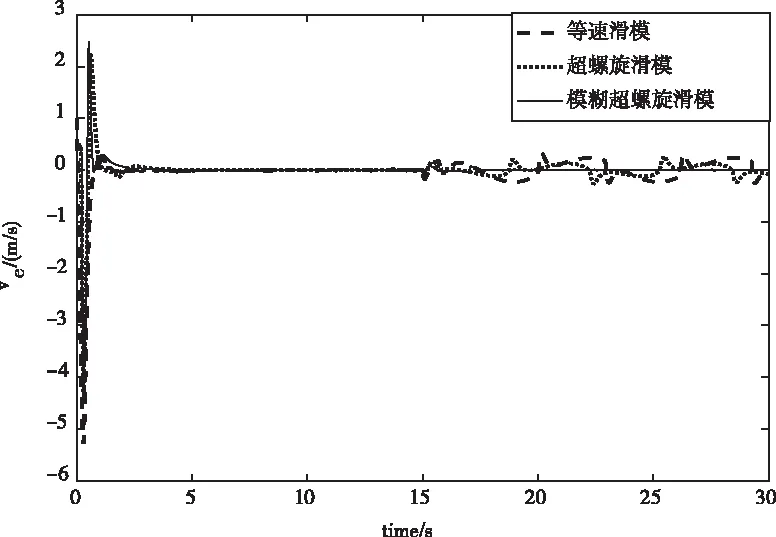
圖7 線速度誤差

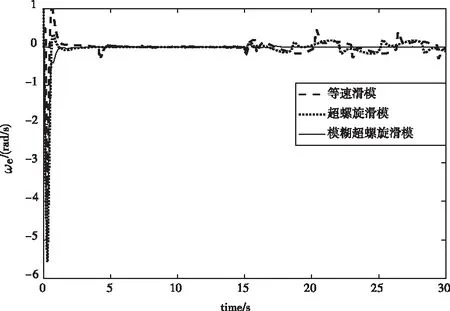
圖8 角速度誤差

圖9～圖10分別為WMR的左、右輪力矩曲線，可以看出，通過設計的抗飽和輔助系統，能夠將執行器的輸出力矩約束在[-τmax，τmax]以內。同時可以發現，超螺旋滑模控制律為正弦型連續控制量，相比于等速滑模，有效的削減了控制量中的抖振。

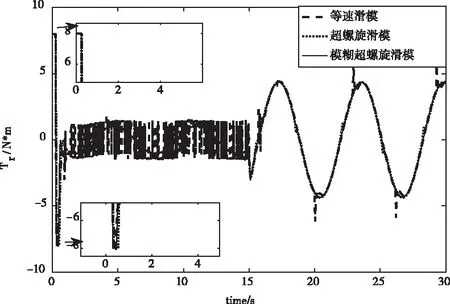
圖9 右輪驅動力矩

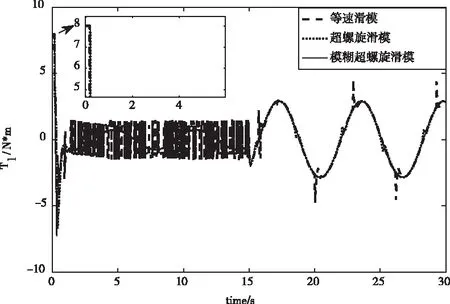
圖10 左輪驅動力矩

采用平方誤差積分(ISE)、絕對誤差積分(IAE)和時間乘絕對誤差積分(ITAE)對軌跡、速度跟蹤性能進行評價，表達式如下。表1～4分別給出了三種控制方法的指標對比，可看出，相較于其它兩種控制方法，本文提出的方法具有最優的性能指標，跟蹤性能更好。

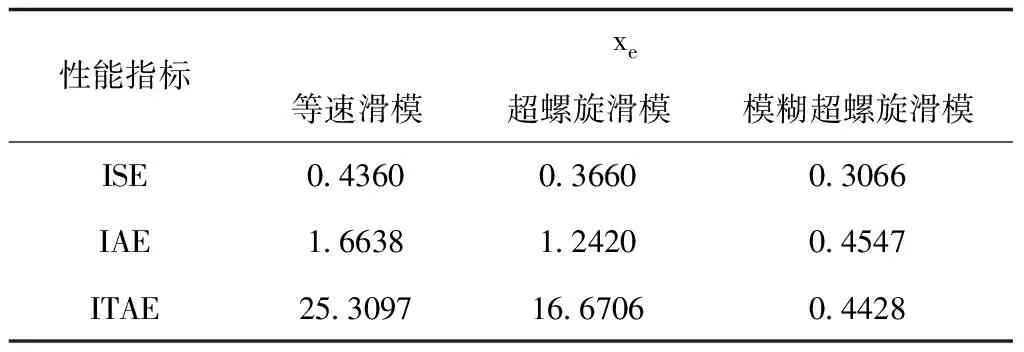
表1 X軸跟蹤性能指標

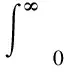
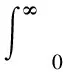
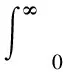
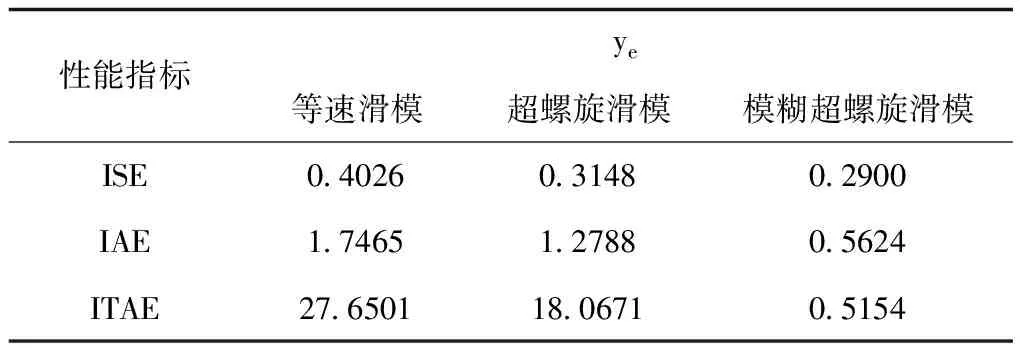
表2 Y軸跟蹤性能指標

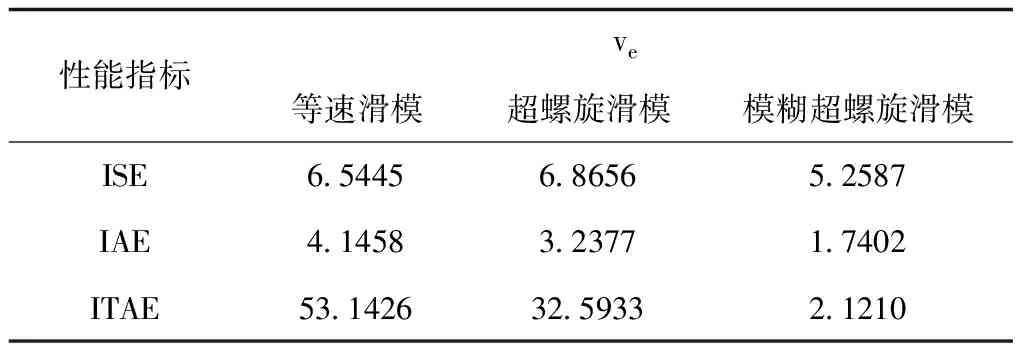
表3 線速度跟蹤性能指標

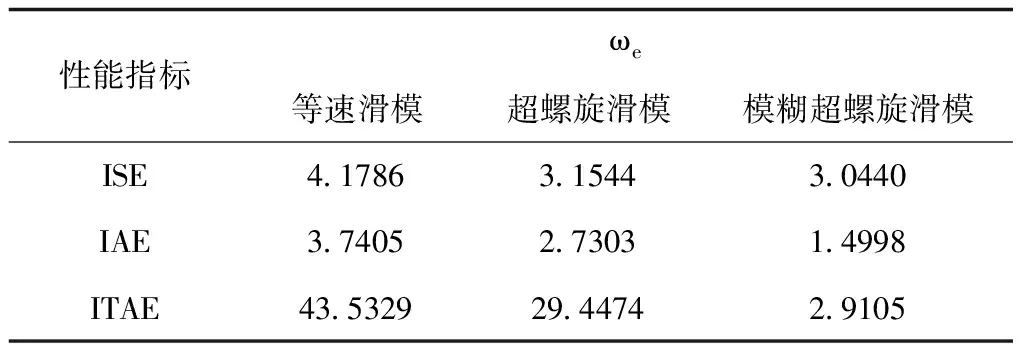
表4 角速度跟蹤性能指標

6 結論

本文針對WMR在側滑、打滑干擾和執行器飽和約束條件下的軌跡跟蹤問題，提出一種抗飽和模糊超螺旋控制策略，通過仿真研究與分析，主要有以下結論：

1)設計的飽和約束輔助系統，能將力矩控制量限制在執行器最大輸出值以內，避免WMR軌跡跟蹤初期出現較大的力矩跳變，實現WMR的抗飽和控制；

2)設計的模糊超螺旋滑模控制律，能克服上界未知的WMR系統擾動，當軌跡跟蹤過程中擾動發生突變、上界改變時，模糊參數自適應律能使軌跡跟蹤誤差和速度跟蹤誤差始終收斂；控制量連續且無抖振；

3)在對比仿真研究中，通過誤差性能指標定量分析三種不同控制策略的跟蹤控制性能，可以得出，所提出的控制策略具有更高的跟蹤精度。

后續工作的重點是結合實際的WMR和嵌入式控制平臺，對本文提出的控制策略進行實驗驗證。