結合融合函數的雙輪機器人二型模糊控制

黃澤瓊，謝小鵬

(華南理工大學機械與汽車工程學院，廣東 廣州 510641)

1 引言

隨著嵌入式以及智能控制的發展，雙輪自平衡機器人在許多領域已經廣泛開展研究和投入使用[1]。雙輪機器人的體積較小，轉彎半徑小使得其運動更加靈活。這類機器人在靜態下是個典型的不穩定結構，必須實時依靠雙輪移動來保持平衡[2]。也正是因為雙輪機器人的高度不確定性、耦合性和非線性等引起了諸多學者對其運動模型和控制策略的研究[3]。

目前，已有許多控制技術被應用于自平衡機器人，如傳統的PID控制、滑模(Sliding Mode)控制、狀態反饋極點配置控制器和模糊控制等[4-5]。

傳統的PID控制器在被控系統高度復雜且非線性的情況下通常是無效的。因此，許多研究者試圖將PID控制器與模糊邏輯控制器(FLC)相結合，以達到比傳統PID控制器更好的系統性能[6]。現有運用在雙輪機器人上的模糊控制大多集中于一型模糊集合(T1-FSs)，然而在實際工程應用中，一型模糊推理的前件和后件隸屬度函數本身具有很大不確定性，當隸屬函數不合適時，模糊系統也無法滿足控制要求。當系統參數或外界情況改變時，一型模糊系統直接處理數據不確定性的能力變得有限。Zadeh在1975年引入的二型模糊集(T2-FSs)能夠對這種不確定性進行建模，二型模糊將不確定性引入模糊集，使得模糊集隸屬函數具有“三維”特性和“寬帶”效應，提高了系統的抗噪聲能力和未知數據處理能力。因此，本文根據T2-FLS設計了二型模糊PID控制器，給與實際工程情況提供了額外的自由度，使得在無法準確確定隸屬度函數的情況下，控制系統的自適應性和魯棒性明顯增強。

另外，由于雙輪自平衡機器人系統的輸出變量較多的特點，若對每個輸出量直接使用模糊理論全部模糊化，會產生維度爆炸的現象[7]，使得系統復雜度大大增加。對此，本文設計了輸出控制量的融合函數，根據線性二次型最優理論并結合歸一化思想，將輸出信息進行融合，有效簡化了模糊控制系統。將上述方法在MATLAB/SIMULINK中實現并驗證了控制系統的可行性。

2 兩輪自平衡機器人運動建模

典型的兩輪自平衡機器人主要包括一對相同的車輪、底盤、驅動器、機身和運動控制單元等部分，結構示意見圖1。兩輪平衡機器人本質上是一種二維移動倒立擺，兩個車輪分別獨立驅動，對稱安裝在機體的左右兩端。在沒有外力驅動下，雙輪機器人是個不穩定的系統，會向一邊自然倒下。因此，機器人必須通過自身不斷的前后運動來控制動態下的平衡。

圖1 自平衡機器人受力分析

該機器人平衡控制的基本思想是：當測量機體傾角的加速度傳感器檢測到機體產生傾斜時，控制系統根據傾角產生一個相應的力矩，通過控制電機，驅動兩個車輪向機身要倒下的方向運動，以保持機器人自身的動態平衡。

圖1中：M表示機器人機體質量，D為兩輪之間的距離，L表示輪軸與機體重心之間的距離，θ為機身的俯仰角度，xl和xr分別為左輪右輪的位移，Hl和Hr表示機體與左輪和右輪之間相互作用力的x軸分量，Vl和Vr為機體與左輪和右輪之間相互作用力的y軸分量；Cl和Cr表示左輪電機和右輪電機的輸出轉矩；xp和yp表示機器人機體質心的位移。

可以得到基于運動學方程的兩輪機器人系統非線性數學模型[8]，具體方程式如下

(1)

Jp=MgLsinθ-ML2sin2θ-

(2)

R為左輪和右輪的半徑，m為左輪和右輪的質量，Jp為機體對z軸的轉動慣量，Jω為左、右輪對轉軸的轉動慣量，ω為y軸與機體的夾角角速度，x為左輪與右輪轉軸中心的位移。

(3)

為簡化表達，令

N=(2JpR2+2L2MR2)m+JpMR2+2JpJω+2L2MJω

(4)

那么(3)式中的參數可以表示為

(5)

將平衡機器人的位移和傾角作為控制系統的輸出，即y=[xθ]T，可以得到輸出方程為

(6)

3 整體控制系統設計

3.1 信息融合函數設計

平衡機器人是個典型的多輸入多輸出系統，本文設計的系統有位移、速度、傾斜角和角速度4個輸出變量。使用區間二型模糊控制，若每個變量僅采用5個模糊子集，就會有54=625個規則數；若要達到模糊系統更加平滑的控制要求，使用7個模糊子集，規則數更是達到74=2401個，顯然這樣復雜的系統難以設計，并且過于龐大不便于投入實際應用。

由于本文所研究的系統的四個內部變量具有很強的耦合性和內部相關性，同時系統的輸出信息也具有直接的耦合性，因此可以構造線性融合函數來實現降維和簡化模糊控制器的設計。將平衡機器人的四個狀態變量集成為誤差E和誤差變化EC，再輸入模糊系統進行設計模糊規則。

1)根據線性二次型最優理論，結合平衡機器人的狀態方程，給定性能指標

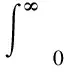
(7)

(8)

控制量為u=KXT，由最優控制理論，可求出增益矩陣K：

K=(BTPB+R)-1(BTPA)

(9)

其中P可以由下式的Ricatti方程得到

ATPA-ATPB(BTPB+R)-1BTPA+Q=P

(10)

根據機器人運動的控制要求，主要優先穩定傾角，使機器人保持直立；運動速度次之，使整體機器人保持勻速運動。選擇合適的加權矩陣Q和R，調整控制器參數后，反復試驗，取R=1，權矩陣Q為對角矩陣

Q=diag(1，5，8，1)

(11)

2)將上述所得的增益矩陣K進行歸一化，歸一化后再設計成狀態融合函數。首先選取矩陣K的歐幾里德范數(2-范數)作為歸一化的除數，2-范數計算如下

(12)

根據得到的范數構造融合函數F

(13)

3)將融合函數作為狀態反饋變量的乘積因子即可得到模糊系統的輸入

(14)

3.2 雙閉環二型模糊自適應PID控制

傳統平衡機器人的控制系統使用雙閉環PID控制，內環控制機體傾角平衡，外環控制機器人行走的運動速度或位移。本文設計使用區間二型模糊自適應PID控制對系統進行改進，對每一個閉環引入二型模糊控制來動態整定PID的比例、微分、積分增益。控制系統的整體設計如圖2所示。

圖2 雙輪平衡機器人控制系統

控制系統中，內環直接使用平衡機器人的傾角和傾角速度信息，通過一個雙輸入雙輸出二型模糊控制器，獲取PD控制器的比例增益和微分增益，對機體傾角進行反饋控制，使得機器人首先能保持平衡。外環使用平衡機器人的位移、速度、傾角和傾角速度信息，經過信息融合函數，得到二維模糊控制器的兩個輸入，設計一個雙輸入三輸出的區間二型模糊模糊控制系統，輸出比例增益增量Δkp、積分增益增量Δki和微分增益增量Δkd，對PID控制器進行參數整定，最后PID控制器對機器人的速度進行控制。

4 區間二型模糊控制算法

4.1 區間二型模糊集合的定義

二型模糊集合的概念是由一型模糊集合擴展而來[9]。一型模糊集合的隸屬度是精確的函數，但是現實環境總是存在高度模糊的信息無法準確定義隸屬值，而二型模糊則是將模糊集中隸屬度值再次模糊，使其可以直接處理模糊規則的不確定性，成為了解決現實環境中高不確定性問題的有效手段[10]。

(15)

(16)

(17)

FOU作為二型模糊中一個很重要的概念，體現了模糊集合的主隸屬函數存在的不確定性范圍，不確定域的選取也影響著模糊推理的準確性。

4.2 區間二型模糊控制系統設計

一型模糊邏輯系統(T1-FLS)和二型模糊推理系統(T2-FLS)都有相同的四個部分，即模糊器、規則庫、模糊推理機和輸出解模糊接口[11]。此外，與T1-FLS不同，T2-FLS要先將推理機的模糊集合輸出經過降型器(Type Reducer)再進入解模糊接口。控制系統結構如圖3所示。

圖3 二型模糊邏輯系統

根據本文的控制對象平衡機器人，設計兩個模糊控制器。第一個是在內環控制平衡傾角的二型模糊自適應PD控制器；第二個是在外環控制直行速度的區間二型模糊自適應PID控制器。

內環控制平衡的區間二型模糊控制器規則是

外環控制速度的區間二型模糊控制器規則是：

其中規則前件是函數融合后的E和EC兩個變量，E的范圍是[-0.6，0.6]，EC的范圍是[-0.9，0.9]。規則后件是PID控制器的3個參數增量：比例增益增量Δkp、積分增益增量Δki和微分增益增量Δkd。模糊系統的每個輸入和輸出變量分別模糊化為7個三角形模糊子集，分別用NB、NM、NS、Z、PS、PM和PB表示。輸入變量E和EC的上隸屬度函數、下隸屬度函數和不確定域(FOU)如圖4、圖5所示。

圖4 輸入變量E不確定域

圖5 輸入變量EC不確定域

一共建立7x7=49條變量融合后的E、EC與Δkp、Δki、Δkd之間的模糊推理規則，這些規則可以通過區間二型模糊系統的輸出曲面展現出來。Δkp、Δki、Δkd輸出控制的三維曲面如圖6、圖7、圖8所示。

圖6 Δkp輸出控制曲面

圖7 Δki輸出控制曲面

圖8 Δkd輸出控制曲面

設計的區間二型模糊控制器使用“karnikmendel”(KM)方法進行降型，解模糊方法使用面積重心法[12]。

5 仿真分析

針對兩輪平衡機器人的運動模型，使用本文提出的雙閉環區間二型模糊控制系統，結合信息融合函數對其進行平衡控制和速度控制。設計實驗考慮到機器人在不同的初始狀態、不同的運動速度目標、擾動作用以及參數不確定性下的控制效果，同時與雙閉環PID系統進行對比，驗證本文算法的可行性與優越性。

5.1 平衡控制

圖9 傾角變化曲線

圖10 速度變化曲線

從中可以看出本文提出的T2FLC控制算法使得機器人在1.7s左右恢復傾角為0，即機器人平衡直立狀態，同時速度為0，即保持靜止；而PID控制器需要2.5 s左右使機器人保持平衡。

5.2 速度控制

圖11 傾角變化曲線

圖12 速度變化曲線

從曲線中可以看出平衡機器人從靜止加速到0.7m/s并保持直立穩定狀態，使用二型模糊控制只需1.6秒，而使用傳統雙閉環PID需要3秒左右。在整體速度調整過程中，二型模糊控制表現的更加平穩，傾角超調量也較小。

5.3 增加干擾

考慮增加擾動的情況，仍然以零狀態變量為初始條件，設定目標速度為1m/s，當機器人達到目標速度且保持穩定之后，在t=5s時施加一個峰值為5的瞬時輸入擾動，比較PID和T2FLC的控制效果，傾角和速度響應曲線如下圖所示。

圖13 傾角變化曲線

圖14 速度變化曲線

在第5秒時，平衡機器人遇到干擾，此時傾角和速度都出現較大的波動，控制器對其進行調整，從曲線中可以看出二型模糊控制響應更快，在第6秒左右就重新恢復了機身平衡，同時也恢復速度到1m/s，而PID控制在第7秒左右才恢復原狀態。

5.4 參數不確定

圖15 傾角變化曲線

圖16 速度變化曲線

在參數改變后可以看到，傳統PID持續振蕩且振幅衰減較慢，不能快速反應使機器人保持平衡，直到10秒之后依然有輕微振蕩；而T2FLC控制下的平衡機器人在4秒之后就達到穩定，并且達到了1m/s的速度要求。

6 結論

本文對于雙輪自平衡機器人，設計了用于控制直立平衡和行走速度的區間二型模糊控制器(T2FLC)，并且考慮到模糊控制自身規則繁多的問題，使用函數融合的方法，簡化控制系統的復雜度。使得模糊控制器在減少規則數量、平滑控制輸出和優化控制響應性能等方面具有更大的優勢。仿真結果表明，二型模糊PID控制器比傳統的雙閉環PID控制具有更佳的性能效果。具體而言，在相同初始條件下，T2FLC使機器人更快達到穩定平衡狀態；在速度控制中，T2FLC可以迅速加速到預定速度并保持穩定。另外，本文還考慮了輸入擾動和機器人參數不確定下的控制效果，仿真結果表明，T2FLC在應對擾動時可以快速調整PID參數，使得機器人較快恢復平衡，具有較強抗干擾能力；當機器人自身參數存在不確定性時，傳統PID控制下機器人已經出現大幅抖動且衰減緩慢，而T2FLC仍可以快速反應并進行有效控制。未來將在機器人轉向控制和硬件實現的方向上繼續研究，以進一步驗證和發展本文提出的算法。