蓄電池式地下鏟運機動力電池的電磁輻射干擾研究

□趙云霄 楊忠炯

為了響應國家節能環保的號召，各種以電能為主要能源的工程機械車輛也如雨后春筍般紛紛問世。然而，就現階段而言致力于地下挖掘、運輸的地下鏟運機在新能源領域仍處于起步階段[1]。目前，新能源地下鏟運機一般為裝載有電纜的電纜式地下鏟運機，電纜式地下鏟運機雖然解決了排放和能源的問題，但是由于電纜長度的局限性，導致鏟運機的作業距離不能過于遠離配電站，從而限制了鏟運機的機動性能和活動范圍，也限制了運行速度，這無疑大大降低了電纜式鏟運機的經濟性。為此，提出一種以蓄電池為主要能源的新型純電動地下鏟運機，該電動鏟運機能解決傳統地下鏟運機尾氣排放嚴重造成井下環境惡劣的難題，也能解決電纜式電動鏟運機機動性受到限制的困擾。

然而，蓄電池式地下鏟運機的動力電池在工作時帶來的大電壓和大電流很有可能產生比較嚴重的電磁干擾；而且蓄電池本身體積較大，占用了很大一部分空間，勢必導致鏟運機內部的電磁環境復雜。以上所述因素很有可能對蓄電池式地下鏟運機車載的各類敏感電氣設備造成不良影響。本文以蓄電池式地下鏟運機的動力電池為電磁輻射干擾源，對其產生的電磁輻射干擾進行研究。目前國內對于蓄電池式地下鏟運機的研究還比較少，具有一定的創新意義。

一、電池模組

本文所研究的某型號蓄電池式地下鏟運機的動力電池分布情況的三維模型和二維俯視圖如圖1(a)和圖1(b)所示。圖1(a)中綠色和黃色模塊為提供電能的電池模組，紫紅色部分為敏感元件預定放置位置。其余部分為鏟運機后車架其他結構的簡化模型。

根據電池廠商提供的相關設計方案，該型號蓄電池式地下鏟運機需要裝載36塊電池模組以滿足實際工作所需的供電要求。36塊電池模組基于鏟運機實際結構要求考慮放置在鏟運機后車架處。

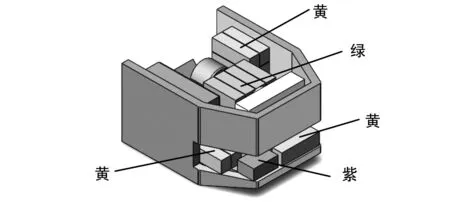
圖1(a) 電池分布情況三維模型

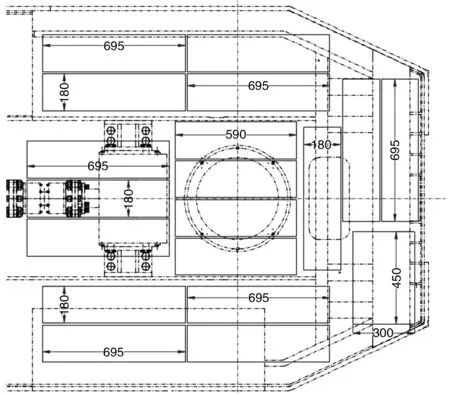
圖1(b) 電池分布情況二維圖

作為蓄電池式地下鏟運機電能動力來源的36塊電池模組由兩類電池模組組成，分別為I類電池模組和II類電池模組。其中I類電池模組有16個，I類電池模組的單元尺寸為590mm×180mm×220mm，在圖1中以綠色部分表示；II類電池模組有20個，II類電池模組的單元尺寸為695mm×180mm×220mm，在圖1中以黃色部分表示。I類電池模組和II電池模組的實物如圖2(a)、圖2(b)所示。

36塊電池模組組成一個整體作為鏟運機的動力電池，其總電量為205KWh，電壓582.4V，電芯類型為LFP(磷酸鐵鋰)。

圖2(a) I類電池模組

圖2(b) II類電池模組

基于圖1所示鏟運機后車架的三維模型可以明顯發現，動力電池組占用鏟運機后車架的空間較大，勢必導致此處空間電磁環境復雜，需要進行系統的仿真計算和研究。

二、電磁場算法和仿真

目前電磁場仿真分析常用的數值計算方法主要有：矩量法、有限元法、有限積分法、傳輸線法、時域有限差分法等。經過多方面綜合考慮，本文所采用的仿真計算的數值計算方法是矩量法。

采用矩量法解決電磁場問題的優點是該方法比較嚴謹地計算了多個系統之間的互相耦合并且保障了誤差系統整體最小從而不產生數值色散，比較適合應用在計算電大尺寸的電磁場問題，非常適合本文所要做的工作。

(一)矩量法的基本原理。矩量法事實上就是將積分方程、微分方程、差分方程轉化為矩陣方程，然后對該矩陣方程進行求解的方法[2]。因為求解積分方程、微分方程、差分方程等算子方程的過程中必須要計算矩量，所以該方法被稱作矩量法。下面是矩量法求解的具體步驟：

對于非齊次方程

L(f)=g

(1)

式(1)中L是線性的算子方程；g可以是類似于激勵源之類的已知函數，f可以是類似于表面電流之類的未知函數。

令f在算子方程L的定義域中展開為一組線性無關的基函數f1，f2，f3，…fn的組合，即：

(2)

式(2)中αn是系數，fn是展開函數或者是基函數。將式(2)代入式(1)，再用L算子的線性我們就可以將公式(1)變為：

(3)

于是，求解f的問題可以變成求解αn。

定義一個合適的內積〈f,g〉，在L的值域里定義一個權函數或者檢驗函數集合[ω1，ω2，…，ωn]，對每一個ωm在公式(3)取內積，可以得到：

(4)

式(4)中m=1，2，3…。該方程組可寫成以下矩陣形式

[lmn][αn]=[gm]

(5)

式(5)中

(6)

(7)

得到了[lmn]和[gm]后，對線性方程組求逆，就可以求出[αn]。

[αn]=[lmn]-1[gm]

(8)

將求出的系數[αn]代入式(2)就可以求出未知函數f。

對于任何一個求解的問題，選擇基函數fn和選擇權函數ωn都是非常重要的。

基函數fn需要保證其線性獨立性，而且基函數的線性組合必須良好地逼近未知函數f。而權函數ωn則需要保證其線性無關，并且已知函數g的相對獨立性能決定內積〈ωm,g〉。除此之外，對于基函數fn和權函數ωn的選擇也需要考察以下幾點：一是矩陣是否能求逆；二是矩陣元素是否容易計算；三是精度的要求；四是矩陣是否為良態。

基函數和權函數的選擇是十分關鍵的。就基函數來說，雖然在理論上可以選取所有保證線性獨立性的基函數，但是可以不錯地逼近未知函數f的基函數在實際應用中相對較少。

被選擇的基函數需要使得矩陣達到下列幾個要求：較少的階次、求逆簡單、收斂迅速等。基函數可以分成分域基函數和整域基函數兩大類[3]：

(1)分域基函數可以定義為值域存在于未知函數f的所有定義域中，但是有一部分值為0的基函數，比如：

脈沖函數(分段均勻)

分段正弦函數

分段線性函數

(2)整域基函數可以定義為在未知函數f的全部定義域中都存在，且都不為0的基函數，比如

冪級數 fn=x-xn+1

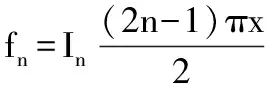
麥克勞林級數 fn=Inx2(n-1)

權函數的匹配方法主要有三種[4]：點匹配法、線匹配法和伽遼金法。

①點匹配法可以定義為匹配位置處于基函數定義域中點位置的方法，這種方法產生的匹配點少而且準確率相對較低。

②伽遼金法所選取的權函數和基函數一樣，這樣在計算的過程中能得到對稱的矩陣從而使得計算的相對誤差大大減少。

③線匹配法可以定義為匹配位置在基函數定義域的中線處的方法，這樣得到的結果計算精度較高而且計算相對較為簡單。

總結一下，矩量法的基本步驟如下：一是將待求的積分、微分、差分等算子方程轉為矩陣方程；二是選擇一組滿足前文所述要求的基函數，將基函數和待求函數線性組合，代入算子方程，從而獲得一組代數方程組；三是用適合的匹配方法得到一組權函數，計算所得代數方程組的廣義矩量[5]，并轉化成矩陣的形式；四是對得到的矩陣方程求逆，將求解得到的系數矩陣代入原方程組，即可得到矩量法的數值解。

(二)矩量法應用于電磁場計算。對于任意介質，麥克斯韋旋度方程為[6]

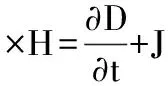
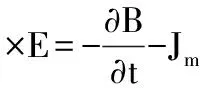
(9)

將理想導體邊界條件代入式(9)可以得到電場的表達式為：

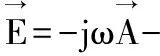
(10)

(11)

(12)

式(11)與式(12)中J是表面電流，σ是表面電流密度，J與σ滿足以下關系：

?S·J=-jωσ

(13)

因為在導體表面，電場的切向分量為0，所以可以得到以下式子：

(14)

現運用RWG基函數法求解電場，定義一個表面電流J的函數組合fn，fn滿足以下關系：

(15)

式(15)中In是與第n個基函數相關的電流展開系數。

選取檢驗函數，定義以下內積：

(16)

使用基函數對式(1～14)進行檢驗，可以得到以下式子：

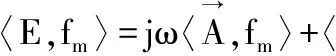
(17)

使用伽略金匹配法選取權函數，選擇的權函數與基函數一致，即ωn=fn。

按照上述矩量法的基本原理可以將電場積分方程轉化為矩陣方程，即：

[Zmn][In]=[Vm],m,n=1,2,...,N

(18)

矩陣[Zmn]與矩陣[Vm]確定后就可以解出式(18)中的[In]，得到電場的解。求解磁場的步驟類似故不再贅述。

(三)仿真計算電池的電磁輻射。目前市面上有各式各樣的電磁仿真軟件，這些仿真軟件各有優劣。本文在諸多電磁仿真軟件中所選用的軟件是FEKO軟件。FEKO軟件由南非EMSS公司開發，采用的主要數值算法有矩量法、多層快速多極子算法、有限元法、PO算法、并行UTD算法等，幫助從業者系統地進行電磁分析研究[7]。

FEKO軟件針對性較強，十分適合車輛的電磁環境建模和仿真，該軟件采用了本文所選取的數值計算方法，矩量法，而且還擁有快速多極子算法，極大地提高了計算效率，比其他仿真軟件更加適用于電大尺寸的電磁仿真分析，非常適用于本文所要做的工作。

選取好合適的電場仿真軟件之后則可以開始進一步的工作。利用SolidWorks建模軟件建立好的鏟運機后車架的三維模型并轉換成x_t格式的文件。將轉換好的x_t格式文件導入到FEKO系列軟件的CADFEKO軟件中，對鏟運機后車架各個結構的相對介電常數進行設置。在CADFEKO軟件中將導入的鏟運機后車架三維模型進行網格化處理。如果單純地考察計算精度這一層面，那么網格化程度越密，則計算造成的誤差越小，可如此一來計算的復雜程度將會變的很大，工作效率也會大大降低。但是，如果網格化的密度太疏又會導致計算不夠精確，從而影響仿真結果的準確性。

所以，在選擇網格化計算精度時需要同時考慮到計算精度要求和實際條件的計算限制。本文在綜合考慮之后選取到了一個合適的計算精度，使其既能滿足預期的計算精度要求又能避免多余冗雜的低效率計算，提高計算效率。

做完上述工作后，在電池分布的位置添加相應的輻射干擾源，將其參數調整到與動力電池工作時一致，電壓582.4V，電芯類型LFP(磷酸鐵鋰)，電量205kWh。仿真頻率范圍設置為1Hz～300kHz，步長為2kHz。利用FEKO仿真軟件計算距離后車架左側面550mm、距離后車架尾部197mm、距離后車架底部高345mm位置處的電場分布和磁場分布，該處為敏感元件初步設計的安裝位置，然后仿真計算觀測點處水平面整體的電場強度和磁場強度，考察敏感元件安裝位置的最優解。

觀測點處電場強度仿真結果如圖3所示。可以得到觀測點處電場強度峰值時頻率為38kHz，查看該頻率下觀測點所在水平面上整體的電場強度分布仿真計算結果，其具體仿真結果如圖4所示，圖4中黑色圓點為觀測點所在水平面中觀測點的位置。

觀測點處的磁場強度仿真結果如圖5所示。可以得到觀測點處磁場強度峰值時頻率為90kHZ，查看該頻率下觀測點所在水平面上整體的磁場強度分布仿真計算結果，其具體仿真結果如圖6所示，圖6中黑色圓點為觀測點所在水平面中觀測點的位置。

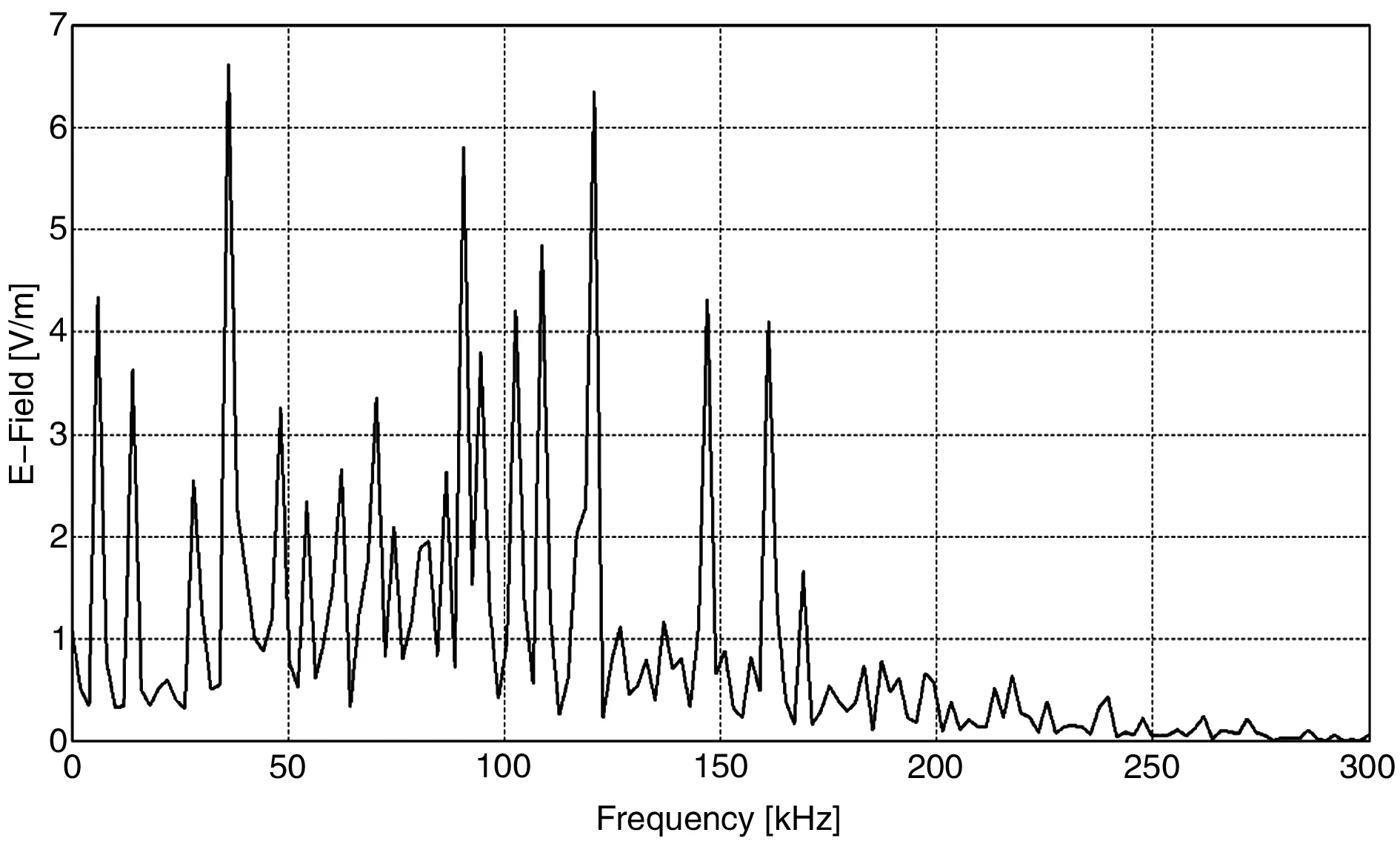
圖3 觀測點電場強度仿真結果

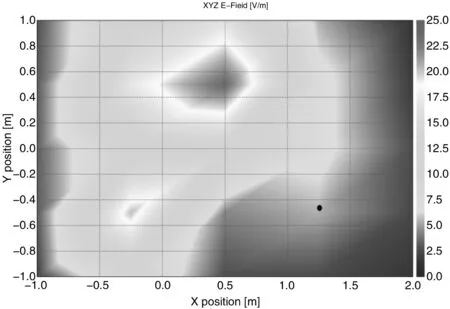
圖4 38kHz時整體電場強度分布仿真結果

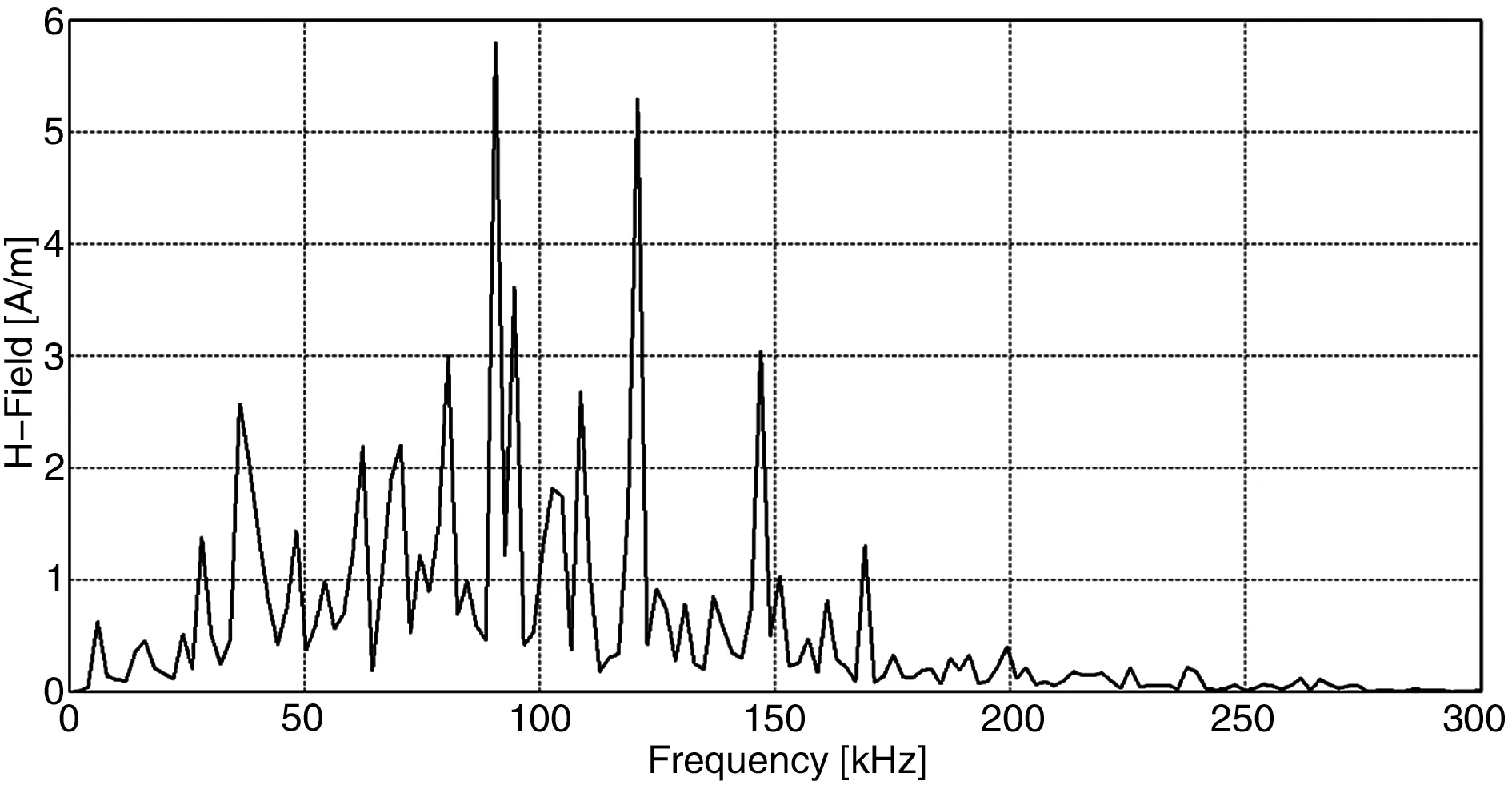
圖5 觀測點磁場強度仿真結果

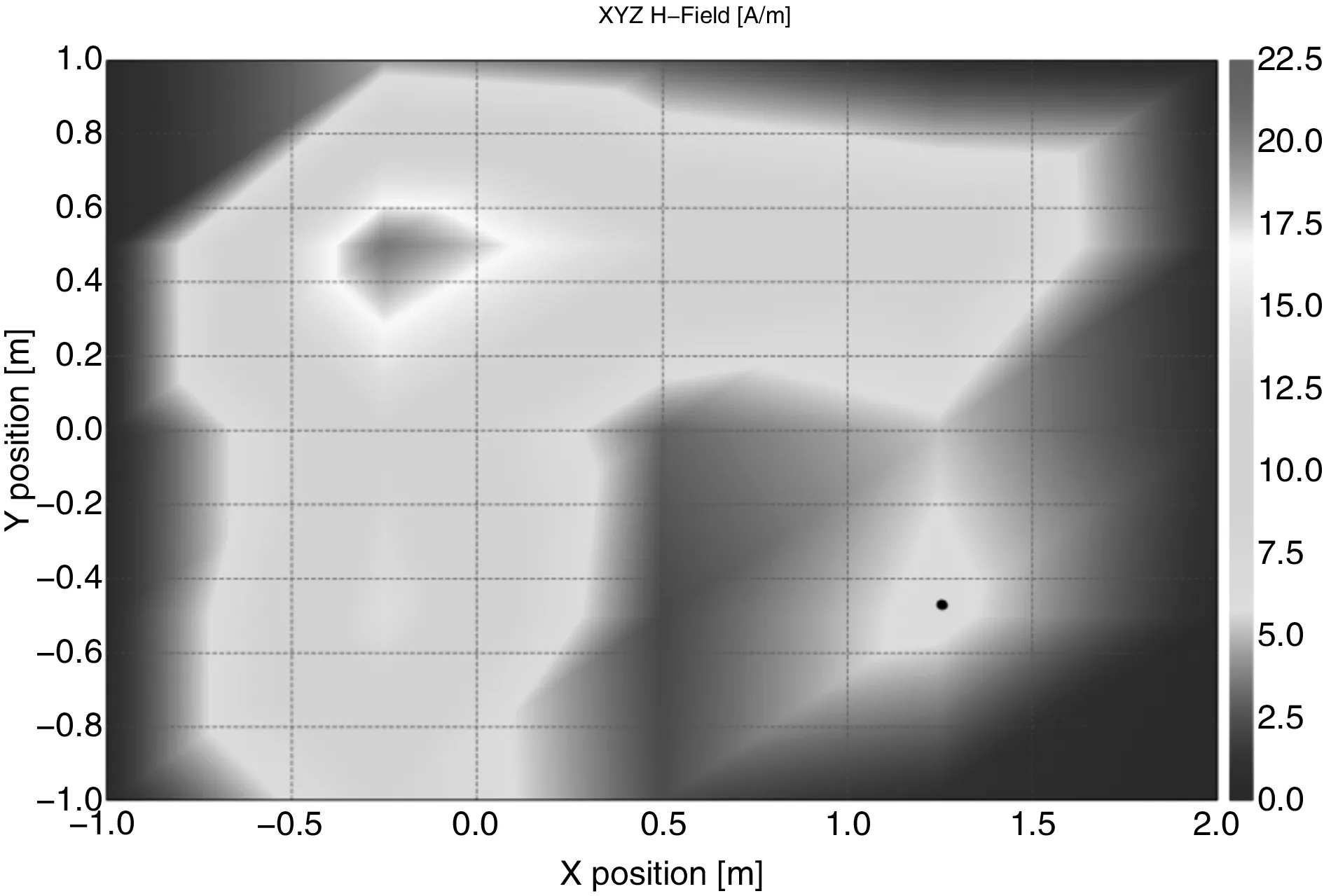
圖6 90kHz時整體磁場強度分布仿真結果

根據以上仿真結果可以得出：

(1)敏感元件處的電場輻射值的范圍是0～6.7V/m，磁場輻射值的范圍是0～5.8A/m，已經超出了該處敏感元件的抗干擾限值5V，可以初步認定需要對蓄電池鏟運機的動力電池工作時產生的電磁輻射進行有效的抑制處理。

(2)敏感元件所在安裝位置需要進行調整，定義后車架前后方向為X方向、左右方向為Y方向。根據電場、磁場整體分布仿真結果來看，將敏感元件安裝位置在X方向上左移400mm，在Y方向上下移150mm會更加理想。

三、結語

本文以某型號蓄電池式地下鏟運機為研究對象，研究其動力電池的工作時產生的電磁輻射干擾。經過分析、建模、選取仿真軟件、進行仿真計算、研究仿真結果等工作，最后初步認定動力電池工作時產生的電磁輻射需要得到抑制。電磁輻射的抑制措施初步可以主要考慮使用鋁或者銅制箱體屏蔽隔離干擾源、屏蔽保護敏感元件、對敏感元件的安裝位置進行調整讓敏感元件遠離輻射源等方法。