數學模型思想滲透的教學與思考

【摘 要】以蘇科版數學教材“用一元二次方程解決問題（1）”為例，從模型回顧、模型建構、模型應用、總結提升四個教學環節闡述教學意圖，分析教學效能。從對模型思想的再認識、對模型思想滲透的再思考、對培養建模能力的再理解三個維度闡釋在初中數學教學中滲透模型思想的策略。

【關鍵詞】初中數學；模型思想；一元二次方程；解決問題

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2022）59-0046-04

【作者簡介】孫凱，江蘇省蘇州市陽山實驗初級中學校（江蘇蘇州，215151）教師，高級教師。

模型思想是數學的基本思想之一，數學模型是數學應用的重要形式，數學建模是應用數學知識解決實際問題的基本手段。

在初中階段，滲透模型思想是培養初中生數學建模能力的主要路徑。但在實際教學中，教師對模型思想的認識和理解不夠深刻，對模型思想的發掘和滲透不到位，導致學生對數學模型認識模糊、建構模型能力不足。本文以蘇科版數學教材九年級上冊第一章“用一元二次方程解決問題（1）”為例，談談如何在數學教學中滲透建模思想，培養初中生的數學建模能力。

一、教材簡析

1.對教材的理解

“用一元二次方程解決問題”是蘇科版數學教材九年級上冊第一章“一元二次方程”第4節的教學內容，教材在此小節設置了3課時教學內容，每課時編排兩個典型問題。本課為第1課時，教材中設置的兩個問題分別為“面積問題”和“增長率問題”。兩個問題與現實生活緊密聯系，符合初中生的認知基礎和認知經驗，有利于初中生在最近發展區內運用數學知識解決實際問題，使學生在數學建模的過程中體會一元二次方程模型是刻畫現實世界的有效模型。

在教學時，教師不應過于側重實際問題的歸類教學，而應淡化對問題的歸類，將教學重點聚焦于“類屬問題”的本質上——數學模型的建構。這才符合教材編寫者的真實意圖，也是進行實際問題教學的應有之義。

2.教學目標與解析

【教學目標】經歷和體驗用一元二次方程解決“增長率問題”和“面積問題”的過程，進一步體會一元二次方程是刻畫現實世界數量關系的重要數學模型［1］，增強數學應用意識，培養數學建模能力；會根據具體問題中的數量關系列出一元二次方程并求解，能檢驗所得的結果是否符合實際意義；經歷引模、建模、解模、驗模的數學建模過程，進一步提高發現和提出問題、分析和解決實際問題的能力。

【解析】從學生的認知基礎看，在“面積問題”中，建立一元二次方程模型是沒有障礙的。而在“增長率問題”中，學生的認知經驗停留在“一次”增長上，往往對“二次”增長不太理解。因此，教學目標應指向學生經歷和體驗建構數學模型求解問題的過程，重點是滲透模型思想，幫助學生突破認知障礙，使學生在分析求解實際問題的過程中建構不同的數學模型，培養數學建模能力。

二、教學過程

（一）模型回顧

引問：母親節期間，鮮花店里的某種鮮花價格上浮了20%，小明花18元買了一束鮮花送給媽媽，求這束鮮花原來的價格。

【教學意圖】本環節對教材上的問題順序進行了調整，先呈現增長率問題，從學生熟悉的“一次”增長問題著手，為“二次”增長的學習奠定基礎，有利于學生回顧用方程求解實際問題的一般步驟，喚醒其建構方程模型求解實際問題的認知經驗。

【效能分析】學生能理解“引問”中的數量關系，并總結用一元一次方程解決問題的一般步驟——審題、設未知數、找等量關系、列方程、求解、檢驗、作答。本題使學生初步體會從“起始數”到“終端數”的變化規律，初步感悟一次增長的數學結構特征，為二次增長模型的學習奠定基礎。

（二）模型建構

【問題1】某商店6月份的利潤是2500元，要使8月份的利潤達到3600元，平均每月利潤增長的百分率是多少？

【教學意圖】問題1屬于“二次增長型”增長率問題。在引問的基礎上，促進學生遷移認知經驗，將“一次增長模型”拓展至“二次增長模型”，建立一元二次方程模型，使學生經歷引模、建模、解模、驗模的數學建模活動過程，對獲得的數學模型進一步抽象、概括，形成“增長率模型”a（1+x）2=b。

【效能分析】學生在“一次”增長的認知基礎上獲得一元二次方程模型2500（1+x）2=3600。在求解該方程模型時，教師應引導學生思考選用哪種解法比較合理，幫助學生完成求解模型的任務。在此環節，適時滲透模型思想，進一步引導學生將“起始數2500”和“終端數3600”符號化，使學生體會一類實際問題中穩定的數學結構，用數學模型的視角理解實際問題中蘊含的數學本質。

【問題2】在淘寶網上購買了60m的柵欄圍成矩形場地。（1）寫出圍成的矩形場地面積y（m2）與長x（m）之間的關系式；（2）能圍成面積為200m2的矩形場地嗎？（3）能圍成面積為240m2的矩形場地嗎？

追問：你能提出一個有關面積的問題嗎？

【教學意圖】問題2屬于“矩形面積”問題。教師可先安排學生畫圖，引導其從幾何直觀的視角體會面積問題，感悟數學模型的幾何意義。在60m柵欄的實際背景下，設置了3個問題。第一個問題驅動學生獲得函數模型y=x（30-x），感悟矩形面積會隨長度的變化而變化，為建構一元二次方程模型奠定基礎。后兩個問題涉及具體的矩形面積，即對面積y賦值，將函數模型轉化為方程模型，驅使學生自覺感悟函數（二次函數）與方程（一元二次方程）的內在聯系。追問環節預設學生會提出矩形場地面積最大的問題，引導學生運用“配方法”求最值，為后續研究二次函數的圖象和性質打下堅實基礎。

【效能分析】學生能畫出矩形輔助分析問題，寫出y=x（30-x）的函數模型，進一步將y更換為200或240，求解一元二次方程，獲得數學結果。在追問環節，學生能說出“圍成正方形時面積最大”，但面對“為什么圍成正方形時面積最大”這一問題，學生往往不能作出合理解釋。此時，教師應注重引導學生運用配方法解決最大值問題。

（三）模型應用

【習題】1.某服裝原價每件80元，經過兩次降價，現售價每件51.2元。求該種服裝平均每次降價的百分率。

2.某商品連續兩次降價10%后價格為a元，則該商品的原價為（? ）。

A. [a/1.21]元? ?B. 1.12a元

C. [a/0.81]元? ?D. 0.81a元

3.一塊長方形菜地的面積是150m2。如果它的長減少5m，那么它就成為正方形菜地。求這個長方形菜地的長和寬。

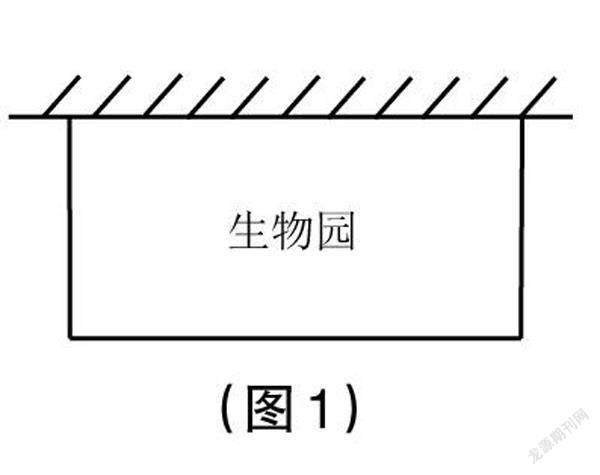
4.學校打算用長16m的籬笆圍成一個長方形的生物園飼養小兔，生物園的一面靠墻（如圖1），面積是30m2。求生物園的長和寬。

【教學意圖】本環節的4個問題分別對應了增長率模型和面積模型。其中題1、題2是對增長率模型的拓展，將“增長”拓展至“降低”，使學生在解決“新問題”的過程中體悟實際問題背后蘊含的數學本質，將數學模型進一步完善為a（1±x）2=b。題3、題4是對面積模型ab=c的實際應用，學生從問題中找到長、寬、周長、面積之間的關系是解決問題的關鍵。

【效能分析】學生從題1中能正確建立一元二次方程模型，但在求解模型時，部分學生出現求解錯誤甚至不會求解的現象。題2相對簡單，學生能正確建立模型并出示結果。題3教師可引導學生畫圖分析題意，完成設、列、解、驗等步驟。在題4中，學生在建立模型求解出結果后，有很多學生不知道或者不會檢驗，因而教學中應及時予以強化。

（四）總結提升

本環節教師安排學生總結學習情況，思考、討論、交流、提升。（板書見圖2）

【教學意圖】引導學生從數學建模的視角總結建立一元二次方程解決問題的過程，滲透模型思想，培養數學建模能力。

【效能分析】借助板書設計總結利用一元二次方程解決問題的數學建模過程，幫助學生體悟模型思想。

三、教學思考

1.對模型思想的再認識

史寧中教授指出數學發展所依賴的思想本質上有三個：抽象、推理、模型。其中模型是數學世界連接外部世界的橋梁。［2］

研究《義務教育數學課程標準（2022年版）》不難發現，課標注重在代數式、方程、不等式和函數等“數與代數”領域內容中滲透模型思想，從而幫助學生建立模型觀念。因此，在代數式、方程、不等式、函數等數學概念教學中，教師應注重引導學生從實際問題情境中抽象出數學對象，進一步建立數學模型，這是教學的關鍵環節。就本節課而言，教師設計適切的實際問題，引導學生建立一元二次方程模型，體會模型思想是教學的核心。因此，在初中學段數學教學尤其是解決實際問題的教學中，引導學生從實際問題情境中發現和提出問題，分析問題，建立數學模型并求解問題，在認知系統中逐步建立模型思想尤為重要。

2.對模型思想滲透的再思考

（1）為什么要滲透

滲透模型思想是義務教育階段的數學教育明確的目標要求［3］，應在發展學生的符號意識、幾何直觀、運算能力、推理能力、模型思想和應用意識等方面有所作為。因此，教師應注重在解決實際問題的過程中滲透模型思想，使學生體會一元二次方程是刻畫現實世界的有效模型。

（2）如何滲透

數學模型思想滲透教學一般分為模型回顧、模型建構、模型應用三個環節。模型回顧是指新模型學習前的認知基礎，通過問題喚醒學生的數學模型認知經驗，為建立新模型奠定基礎。模型建構是指在原有認知基礎上的同化或順應，建立新的數學模型。模型應用是指運用新的數學模型解決實際問題，使學生在建立數學模型解決實際問題的過程中體會模型思想。

本節課模型思想滲透的三個環節以此為基礎，具體為：（1）模型回顧，引導學生回顧曾經研究過的一元一次方程模型，喚醒經驗；（2）模型建構，以問題1、問題2為載體，驅動學生自主建構二次函數、一元二次方程、一元一次不等式（組）等數學模型，體會不同數學模型的特征及內在聯系；（3）模型應用，呈現四個拓展性的問題情境，促使學生運用習得的數學模型解決新的實際問題。

3.對培養建模能力的再理解

在初中階段，教師越來越重視在教學中滲透模型思想，但如何滲透模型思想、哪些教學內容適合滲透、滲透到什么程度等問題依然困擾著很多教師。事實上，滲透模型思想的教學價值指向培養學生的數學建模能力。需要說明的是，在初中數學教學中，滲透模型思想、開展綜合實踐活動是培養初中生數學建模能力的主要路徑，其中滲透模型思想是常規的、適切的、有效的培養路徑。

【參考文獻】

［1］孫凱.在數學建模中建立知識結構——《一元二次方程》單元復習課教學設計與思考［J］.教育研究與評論，2021（2）：45-47.

［2］史寧中.數學思想概論（第一輯）——數量與數量關系的抽象［M］.長春：東北師范大學出版社，2008：1.

［3］周立棟.數學模型思想及其滲透教學［J］.上海教育科研，2015（10）：64-66.

*本文系江蘇省教育科學“十三五”規劃2020年度課題“初中生數學建模能力培養與評價的實踐研究”（B-b/2020/02/104）的研究成果。