基于分布參數模型的高壓輸電線路雙端測距算法研究

戴小劍，田 波，李 愿，喬 華，周 璨，鐘建偉

（1.國網湖北省電力有限公司恩施供電公司，湖北恩施 445000；2.湖北民族大學 信息工程學院，湖北恩施 445000）

引言

單端故障測距算法可利用的已知量太少，從而制約了單端測距算法的發展。隨著信號傳輸技術的發展，采用雙端故障測距算法可以克服單端測距算法的不足，結果較單端測距算法更為準確。

雙端故障測距算法[1]按原理分類有兩種，即兩端數據同步和不同步的算法。兩端數據同步的算法原理相對簡單，但是需要設備來實現兩端數據的同步，初始投入資金較高，測距結果的準確性主要取決于同步裝置對數據同步的精確度，目前大多采用全球定位系統（GPS）的通信方式[2-4]。兩端數據不需要同步的算法減少了硬件設備的資金投入，在實際中更有使用價值，這種算法較復雜，在偽根辨別問題上需要改進。

1 雙端測距算法

1.1 兩端數據需要同步的算法

雙端電源系統的故障測距如圖1 所示，過渡電阻為純電阻性，對稱且線路完全換位。在故障線路中，分別以r、g、L、C代表線路中單位長度的電阻、電導、電感、電容值。故障線路的波傳播常數γ按式（1）計算，波阻抗Zc按式（2）計算。

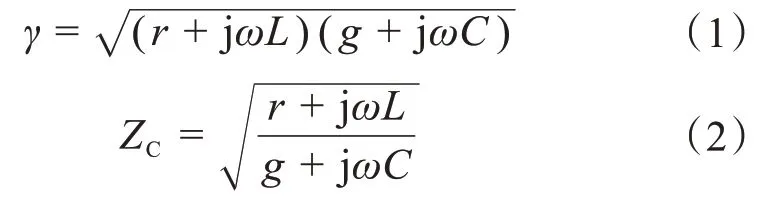
利用P 端電氣量代入均勻傳輸線方程，可以得到故障點電壓為：

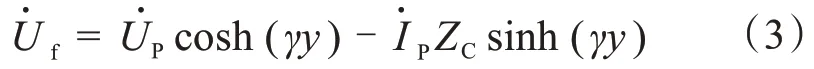
同理利用Q 端電氣量，可以得到故障點電壓為：

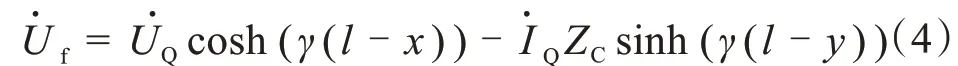
因為故障點電壓不會突變，所以利用兩側電氣量得到的故障點電壓相等，即：

其中，

設γ=α+jβ表，式3.17可以化簡為：

α為波傳播常數γ的實部，α為實數，則：

=A2+B2

所以，可以計算得到故障距離為：

同理，可以得到由β表示的故障距離：

實際的高壓輸電線路上的電抗遠遠小于電阻，電容遠遠大于電導，所以波傳播系數γ的實部遠小于虛部，所以上面分別由α、β表示故障距離。

采用分布參數模型的兩端數據需要同步的雙端測距算法解決了過渡電阻和對端系統阻抗帶來測距誤差的問題，避免了輸電線路分布電容帶來測距的誤差。

1.2 兩端數據不需要同步的算法

采用有不同步角和故障距離兩個未知量的方程求故障距離，可得故障距離為[5]：

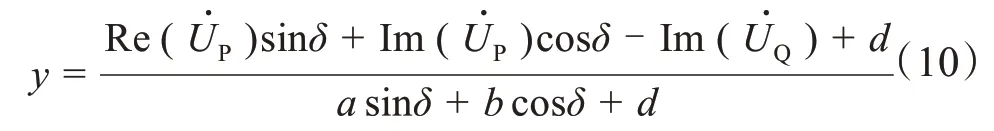
采用兩端電氣量表示的故障點電壓相量幅值相等求故障距離，可得故障距離為：

通過故障距離的公式可以清楚地知道它有兩個解，一真一偽。若其中一個根小于零或者大于L，則這個根是偽根；若大于零且小于L，則這個根為真根，也就是所求的故障距離。

2 雙端故障測距算法決定因素

雙端故障測距算法優于單端故障測距算法。在實際中雙端故障測距算法引入了通信通道，測距結果會產生誤差。

（1）兩端數據不同步

雙端故障測距算法需要保證線路兩側電氣量同步，如果存在不同步角差，無法實現準確測距，通信通道的引入就是為了解決這一問題。

基于通道的同步方法是在主從站間實現實時通信。但是在主從站間建立通信通道，技術要求較高，實現起來比較復雜，勢必造成投入的資金也較大，費用高。利用故障前信息同步的方法比較簡單，投資較小，但是適用范圍有局限性，因為在有些情況下無法獲得線路故障前的信息。基于GPS 的同步方法需依賴GPS來運行，同步誤差不超過1 μs，但是設備造價高，這種同步方法目前應用比較廣泛。

在工程實際中，電壓互感器、電流互感器等對采集的數據會存在一定的延時，即同步技術也是沒有辦法做到數據完全同步的。因此，兩端數據不需要同步的雙端故障測距算法在實際運用中更為廣泛。

（2）線路參數

在系統運行中，外界環境變化會導致輸電線路的參數發生變化，同樣，線路負荷的變化也會引起輸電線路參數的變化。所以，如果在計算中采用固定的線路參數所得到的故障距離必定存在誤差。

（3）線路不完全換位

在計算故障距離時，通常都將線路情況當做三相完全換位。在實際工程中，輸電線路三相完全換位是從線路任意一端看進去的等效換位。當輸電線路故障時，從故障點看，其兩端的線路是不對稱的。因此，在研究不同測距算法時對線路完全換位的假設，實際也對測距精度造成了一定影響。

（4）TA飽和

TA 飽和對故障測距的影響主要是使對端輸送來的電流出現了形變，從而對依據測量端工頻量的測距結果帶來很大的偏差。特別是在大容積特高壓的電力系統中，出現了金屬性短路或者故障出現的地點再經過小阻抗短路，或者在電源、變電站的線路出口附近出現短路，十分容易產生TA 飽和現象。這種現象主要是因為鐵芯的非線性特性造成電流互感器飽和。如果一個鐵芯飽和，它的磁導率會快速下降，而勵磁電流會急劇增大，大部分的一次電流會轉變為勵磁電流，將導致二次電流的嚴重缺損。

解決TA 飽和的辦法主要有兩種，一是補償電流互感器中的飽和電流，二是在測距過程中只使用兩端電壓量或者兩端電壓和對端電流量，以避免TA飽和對測距結果的影響。

（5）故障暫態過程

在實際中，線路故障后會存在一個暫態過程，這會導致故障后的電壓、電流中包含非周期分量、各次諧波分量，對測距結果帶來誤差。減小這一影響的主要方法是在故障測距前進行數字濾波。

3 算例仿真

為檢驗雙端測距算法的測距精度及影響雙端測距算法的因素造成的測距誤差，分別以兩側電壓電流法和兩端數據不同步的算法進行了測距仿真[6-11]。

兩側電壓電流算法解決了單端測距算法無法同時克服過渡電阻和對側系統阻抗影響測距精度的問題，算法簡單易懂，但需要保證兩側電氣量同步。

利用MATLAB/Simulink 構建220 kV 高壓輸電線路模型，仿真模型如圖2。對圖2 設置參數后，可獲得兩側電壓電流法的測距結果。利用兩端電氣量表示的故障點電壓相量幅值相等求故障距離的算法原理[12-15]，兩端數據不同步算法解決了兩側電氣量不同步對測距結果帶來的影響。

圖2 220 kV輸電線路故障仿真模型

4 仿真結果分析

4.1 帶有過渡電阻短路

當線路A 相發生接地短路時，過渡電阻對測距精度的影響如表1～表3所示。由仿真結果可知，兩端電壓電流法不受過渡電阻的影響，在不同過渡電阻下，測距精度基本不變。該算法需要知道兩側數據，兩側系統阻抗均為已知量，故測距精度不受對側系統阻抗影響。

表1 過渡電阻對雙端測距算法的影響

表3 過渡電阻對雙端測距算法的影響

4.2 不同步角差的影響

假設線路A 相經大小為50 Ω 的過渡電阻發生接地短路，不同步角差對測距精度的影響如表4～6所示。由仿真結果可知，不同步角差的存在，導致測距誤差變得很大。因此，兩側電壓電流法測距的準確性建立在兩端數據同步的基礎上，在兩端數據不同步的情況下，這種算法無法準確測距。

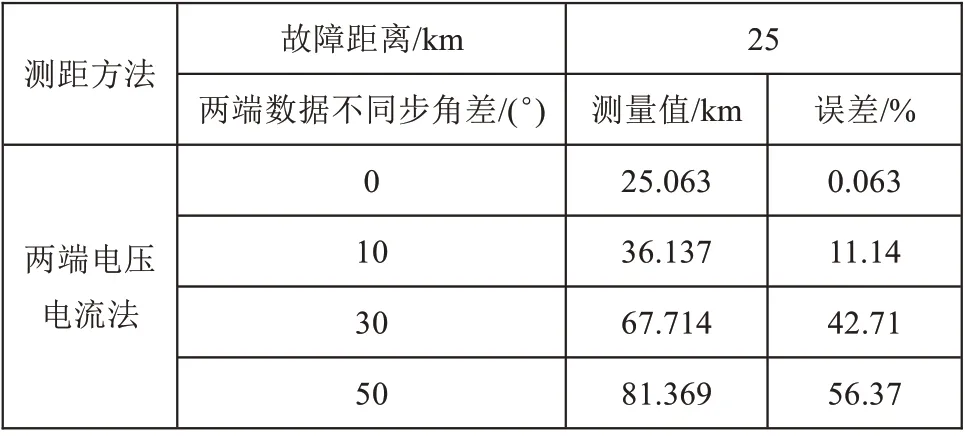
表4 不同步角差的影響

5 結論

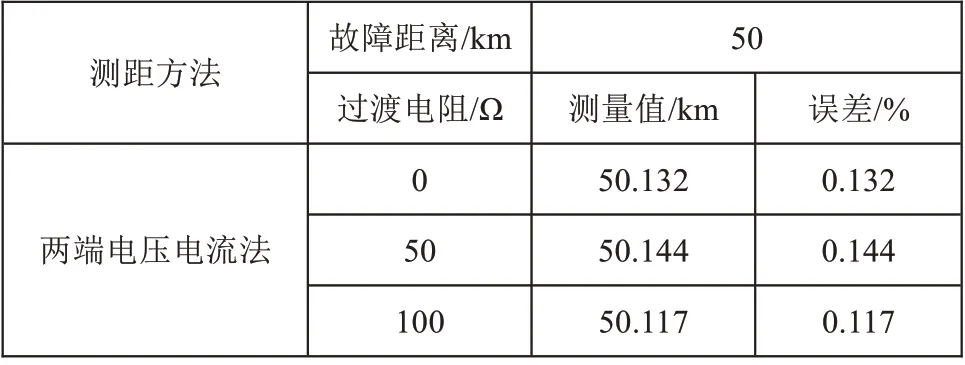
表2 過渡電阻對雙端測距算法的影響

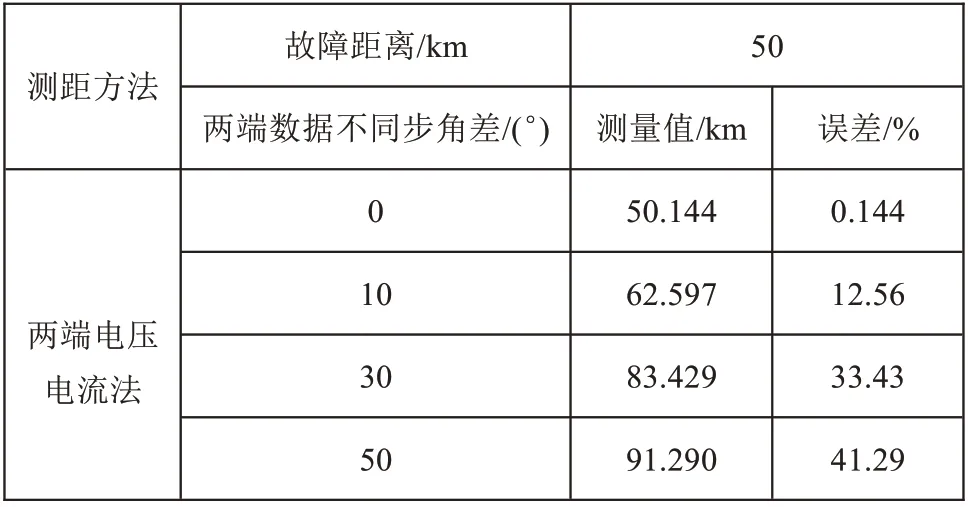
表5 不同步角差的影響

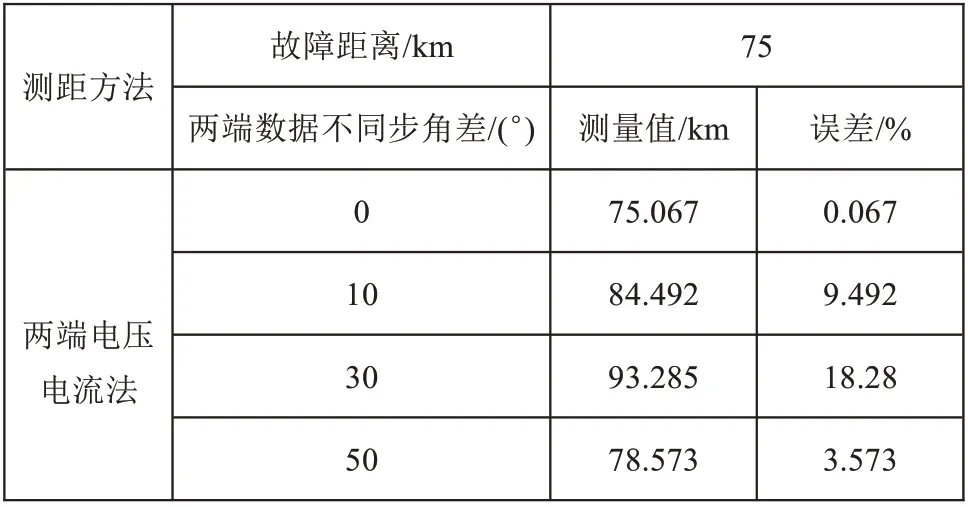
表6 不同步角差的影響

針對數據同步問題，詳細介紹了兩種不需要數據同步的雙端測距算法的基本原理以及優缺點，主要包括采用含有不同步角和故障距離兩個未知數的方程求故障距離的算法和利用兩端電氣量表示的故障點電壓相量幅值相等求故障距離的算法。

在MATLAB/simulink 平臺下，搭建高壓輸電線路仿真模型。仿真結果表明，兩端數據同步算法的測距精度不受過渡電阻的影響，同時兩側系統阻抗為已知量，測距精度也不受對側系統阻抗的影響，但受不同步角差的影響較大，在兩端數據不同步的情況下，無法準確測距。在對各種雙端測距算法分析的基礎上，結合仿真結果，得出各個因素對雙端測距算法的影響。本文提出的雙端測距算法其測距結果更為精確，但其算法原理和計算量較單端測距算法復雜，并且需要建立通信通道保證兩端數據的傳遞，增加了技術難度和投資，還有待于進一步的研究。