基于堆疊稀疏降噪自動編碼器的地區風電場群高精度超短期風電功率預測

吳 卓

（三峽大學 電氣與新能源學院，湖北宜昌 443002）

引言

風電作為可再生能源是電力系統的重要組成部分，但其自身存在間歇性和波動性，因此，風電大規模并網會對電網的穩定運行帶來巨大的安全隱患[1,2]。風電功率預測的精準度對提高風電接入容量和保證電網運行穩定性具有重要意義[3]。超短期預測是預測風電未來4 h 內的出力狀態，將風電未來出力情況由未知變為基本已知[4]。提高風電功率超短期預測精度對滿足電網調度要求具有重要作用。

深度學習網絡在特征提取方面存在很大的優勢，同時，其網絡結構對非線性擬合具有很強的能力，這讓它在電力系統各領域的研究中備受關注。當前，多風電場超短期預測面臨的困難在于風電場數量增加，風電場數據之間的時空關系變得復雜。針對上述研究所存在的問題，提出一種基于堆疊稀疏降噪自動編碼器(Stacked Sparse Denoising Autoencoder，SSDAE)的地區風電場群高精度超短期功率預測方法。該方法降低了對人工經驗的依賴，通過深層網絡提取特征，并對特征進行預測，進一步對預測特征解碼。對輸入的風電功率數據先要加入噪聲，再對加入噪聲后的功率數據進行稀疏性編碼，最終，通過SSDAE來去除加入的噪聲，使其提取輸入數據的本質特征，提高模型的泛化能力。以某地區15 座風電場的實際算例從預測精度驗證了所提方法的有效性。

1 堆疊稀疏降噪自動編碼器

1.1 自動編碼器

自動編碼器(AE)通過無監督學習，降維得到輸入數據的本質特征[5]，結構如圖1 所示，包括編碼器和解碼器兩部分。

圖1 自動編碼器結構圖

自動編碼器的期望輸出z與輸入x相同，在訓練中利用反向傳播算法，以均方誤差損失最小為目標訓練網絡結構的最佳參數θ*，其編碼、解碼和訓練過程可描述如下：

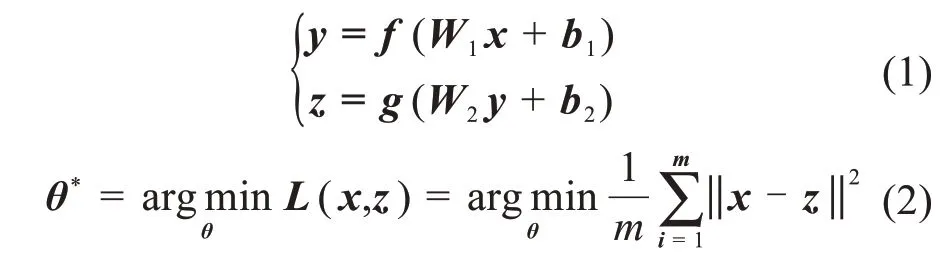
式中，F為隱含層輸出的特征向量，f與g分別為編碼與解碼的激活函數，網絡參數θ=[W1,W2,b1,b2]為編碼和解碼過程中的權重和偏置參數集合，m為訓練樣本個數，L為均方誤差損失函數。

1.2 稀疏自動編碼器

稀疏自動編碼器（Sparse Autoencoder，SAE）是在原有基礎上對自動編碼器的改進，通過對降維后的隱含層數據加入稀疏性約束而得到[6]。

本文神經元的激活函數采用sigmoid 函數。平均稀疏激活度表示為：

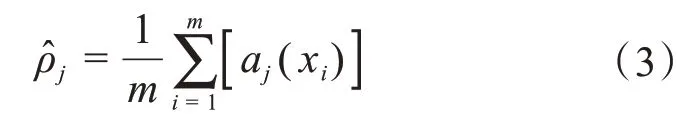
式中，aj為隱含層神經元j的激活值，aj(xi)為輸入xi時隱含層神經元j的激活值。

為了實現稀疏約束條件，通常在損失函數中加入懲罰因子，以達到對自動編碼器的稀疏性限制，使ρ?j的值一直逼近ρ，ρ為稀疏性參數。通常選取相對熵KL(ρ‖ρ?j)作為懲罰因子，其可表示為：

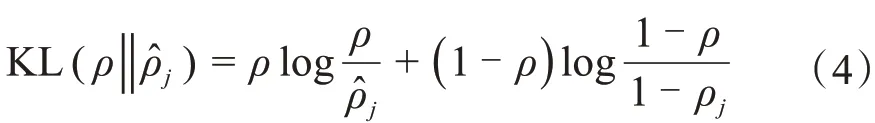
當ρ=ρ?j時，KL(ρ‖ρ?j) = 0，并且隨著ρ?j與ρ之間的差異增大而單調遞增。

稀疏自動編碼器的損失函數表示為：

式中，β為稀疏性限制條件的權重系數。

1.3 堆疊稀疏降噪自動編碼器

降噪自動編碼器（DAE）如圖2 所示，為實現編碼器提取的特征表達更加具有魯棒性，在原有自動編碼器的基礎上對輸入數據加入噪聲，同時防止過擬合問題的發生[7]。

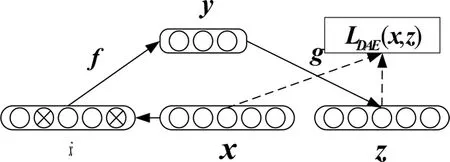
圖2 降噪自動編碼器結構圖

對原始輸入數據x加入噪聲得到干擾輸入x?，然后，利用激活函數f對輸入x?進行特征提取獲得隱含變量y，再利用激活函數g將隱含變量y解碼為輸出z，最后用損函數表示重構誤差，即：

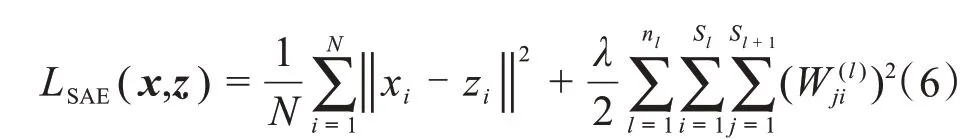
式中，λ為權重衰減系數，ni為神經網絡的層數，Sl為第l層的單元數目。

稀疏降噪自動編碼器（Sparse Denoising Autoencoder，SDAE）的損失函數表示為：

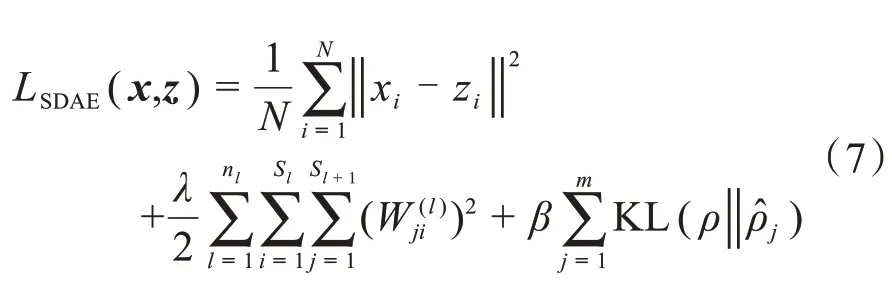
1.4 基于堆疊降噪稀疏自動編碼器的預測結構

顧名思義，堆疊降噪稀疏自動編碼器是通過將兩個稀疏降噪自動編碼器組合生成，前一層稀疏降噪自動編碼器的隱含層作為下層稀疏降噪自動編碼器的輸入，圖3 為基于堆疊降噪稀疏自編碼器的預測結構。它通過逐層的編碼，提取數據的深層特征，在處理具有復雜非線性相關性的高維數據時，能夠實現特征的逐步抽象，最終得到更加有用的特征[7]。

圖3 基于堆疊降噪稀疏自編碼器的預測結構

結構網絡的預訓練過程采用無監督逐層貪婪訓練算法，每次只訓練一個隱含層，此層自動編碼器優化后再開始訓練下一層，直至訓練完最后一個隱藏層，以此來獲取所有層在深度神經網絡中最佳的初始權重，再將最后一個隱藏層的特征輸入到Elman神經網絡采用梯度下降法進行有監督訓練。預訓練完成后，進入微調階段，利用有監督訓練的方式調整模型網絡的權重。堆疊稀疏降噪自動編碼器是運用無監督降維提取特征的方法，而Elman 神經網絡是一種有監督的學習算法，將兩者結合后的預測模型能夠有效預測風電功率數據。

3 算例分析

3.1 算例簡介

算例分析部分采用中國某地區的15 個風電場群，以各風電場全年8760 h 的實測功率樣本數據為分析對象進行未來1 h 的超短期功率預測。樣本分為兩部分：訓練集為對樣本隨機選擇80%，剩余20%樣本作為測試集。

為便于網絡學習與訓練，同時，能夠消除量綱引起的學習不收斂現象，先對輸入功率數據歸一化，過程為：

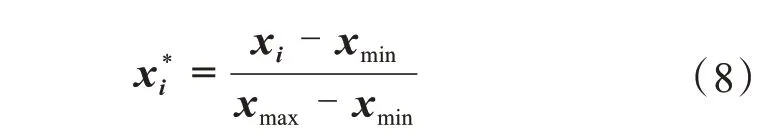
從預測精度來驗證所提方法的應用效果，將SSDAE 模型與AE、SAE 兩種常用降維方法和Elman網絡結合后的預測模型對比，并分析稀疏化、獨立性對降維特征獨立性和降維結果合理性的改善作用。所有程序用Matlab2019a 編寫，在Intel(R)Core(TM)i7CPU@2.30 GHz 計算機運行，預測結果取10次試驗的平均值。表1為網絡參數設置。

表1 網絡參數設置

3.2 評價指標

評價指標采用均方根誤差RMSE 和平均絕對百分誤差MAPE評價預測精度。

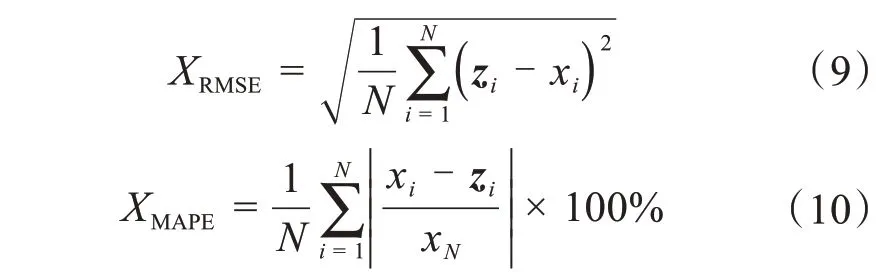
式中，xN為風電場的額定功率。

3.3 預測結果的對比及分析

表2分別給出了多風季與少風季五種模型對18座風電場功率預測結果的誤差統計值和預測時間。圖4為兩季各風電場預測結果的平均絕對百分比誤差XMAPE對比圖。

在預測精度方面，在圖4 和表2 所示信息中可以看出將本文SSDAE 模型與AE 和SAE 兩種模型對比，SSDAE 的平均MAPE 比AE 和SAE 分別降低了3.51%和2.18%。同時，平均RMSE 分別降低了32.8%和19.8%。與此同時，本文方法的MAPE 和RMSE 的最大最小值也都低于兩種對比模型。因此，本文方法能夠獲得更高的預測精度。

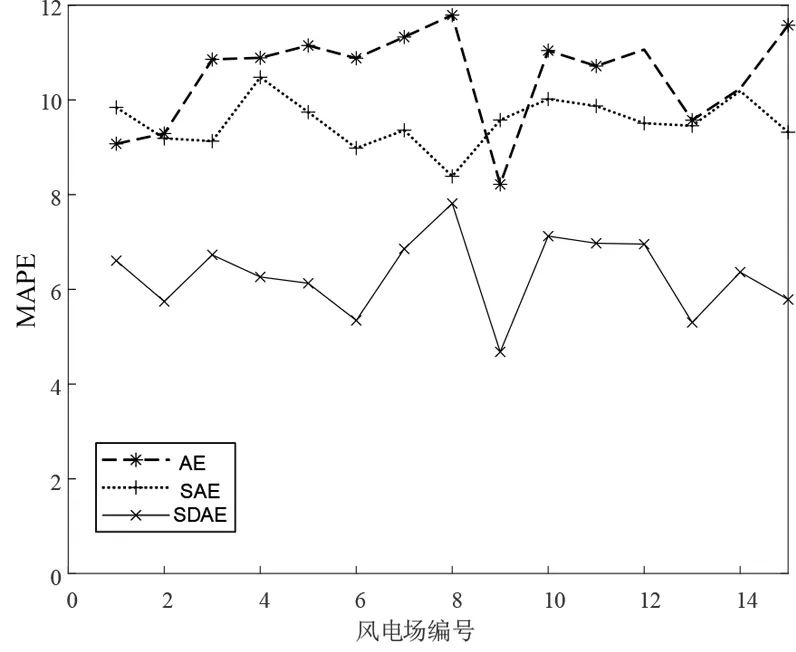
圖4 15座風電場的MAPE誤差對比

表2 15座風電場風電功率預測誤差對比

圖5 所示為在SSDAE 基礎上分別去除稀疏性、降噪性以及將稀疏和降噪性都去除之后的模型的MAPE誤差的對比。

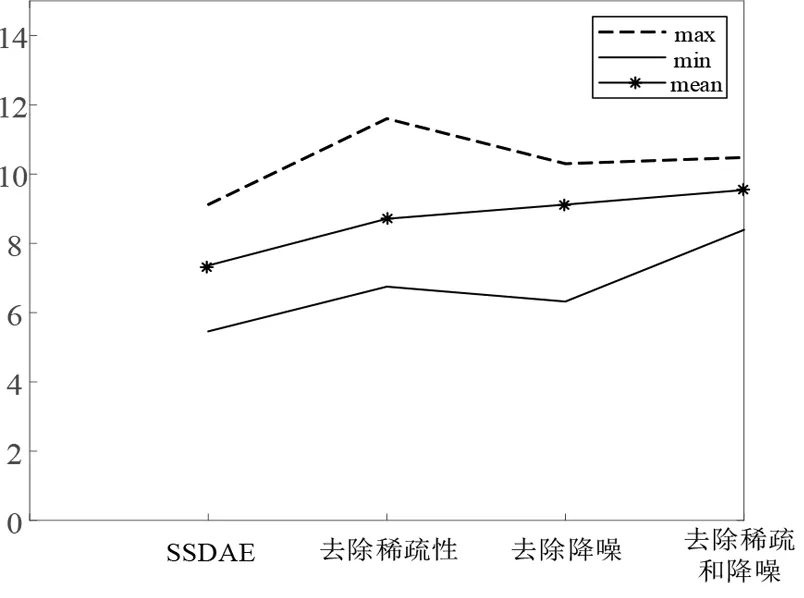
圖5 消融試驗MAPE誤差對比

從圖5 可以看出本文SSDAE 預測模型的平均MAPE 誤差相比于消融試驗的其他模型的平均MAPE誤差最低。并且可以看出稀疏性對模型的影響效果更大一些。在分別去除稀疏性、降噪性以及全部去除稀疏性和降噪性的三種情況下，預測模型的平均MAPE 分別降低了1.35%，1.76%和2.18%。綜上，在SAE 中引入稀疏性和降噪性，能夠有效提高多風電場功率預測精度。

4 結論

為提高提取特征的可靠性和魯棒性，以及進一步提高風電場功率超短期預測的準確性，提出一種基于堆疊稀疏降噪自動編碼器的風電場超短期預測方法。算例分析結果表明，本方法通過引入稀疏性約束和降噪技術改進自動編碼器，使編碼器能夠對風電功率數據進行深度特征提取，學習到的特征表達具備較強的魯棒性，同時，有效提高風電功率的預測精度。相比于其他兩種風功率預測模型，堆疊稀疏降噪自動編碼器的風電場超短期預測方法精確度更高。由于本文只利用風電數據，存在一定的局限性，后續研究可加入氣象信息等因素來進一步提高預測的精確度。