基于FPGA的格密碼關鍵運算模塊的設計與實現*

韓煉冰，房利國，王 松，劉鴻博，楊敏旭

（中國電子科技集團公司第三十研究所，四川 成都 610041）

0 引言

隨著量子計算技術的發展，量子計算機將能在人們可以接受的時間內破解許多目前計算機無法破解的密碼，其中就包括目前大部分公鑰密碼系統所依賴的大整數質數拆分問題和離散對數問題這兩大數學難題。

為應對量子計算機為傳統密碼系統帶來的挑戰，后量子密碼[1]已成為國內外眾多學者的重點研究對象。2016年，美國國家標準與技術研究院（Nation Institute of Standards and Technology，NIST）開始了一項針對抗量子密碼系統的征集計劃，旨在尋找、設計、開發和標準化抗量子密碼系統，以便于在未來取代現有的密碼系統標準。經過3輪的征集提交和篩選，2022年7月NIST發布了首批入圍標準的4個抗量子算法：Crystals-kyber、CRYSTALSDILITHIUM、FALCON和SPHINCS+。這4個算法中有3個基于格的數學難題，另一個使用了散列函數。由此可見，基于格的密碼方案是抗量子計算密碼學中的研究熱點。基于格的密碼算法中的運算大多為線性運算，因此較其他密碼系統，基于格的密碼系統具有計算速度快[2]、密鑰和密文較小等優勢[3]。本文對格密碼中的關鍵模塊——多項式乘法進行研究，給出了一種多項式乘法的運算方法和硬件實現架構，并在現場可編程門陣列（Field Program Gate Array，FPGA）中進行了實現和評估，為格密碼硬件實現提供參考。

1 相關數學基礎

1.1 格密碼數學基礎

線性獨立空間上有集合v1,v2,…,vn∈Rn，格就是這些向量的線性組合，這一過程的表達式為：

式中：系數a均在整數域Z中。任意一組可以生成格的線性無關向量都稱為格的基，格的維度等于格的基中的向量個數。

目前常用的兩個基于格的困難問題是短整數問題（Shortest Integer Problem，SIS）和錯誤學習問題（Learning With Error，LWE），但基于上述兩個問題的加密方案需要的密鑰量大、效率低、資源消耗高，無法在實際中運用。因此，Lyubashevsky等人[4]在LWE的基礎上提出了環上錯誤學習（Ring Learning With Errors，RLWE）問題。基于RLWE的加密方案在性能上有著顯著的優勢[5]，這是現在許多格密碼算法的理論基礎。RLWE在環Zq[x]=f上進行操作，其中f是n項的不可約多項式，通常f=xn+1，其中n是2的冪，q為素數。

1.2 環多項式乘法

對于RLWE密碼算法，其中最為耗時的是環多項式乘法。環多項式乘法有兩種實現方式[6-7]，分別為經典乘法和快速數論變換（Number Theoretic Transform，NTT）乘法。

1.2.1 經典乘法

經典乘法先把多項式a中的每一項與多項式b中的每一項相乘，再把每個多項式相加得到最終結果。如果多項式a和b的最高次項都為n-1，那么計算復雜度為O(n2)，需要n2個乘法和(n-1)2個加減法。

1.2.2 NTT乘法

NTT是基于快速傅里葉變換（Fast Fourier Transform，FFT）實現的，其將FFT中的旋轉因子由復數變成了整數。設正整數序列x(n)，其所有元素均小于模數M，有如下NTT變換[8]：

式（2）為NTT正變換，式（3）為逆NTT變換。其中，a為模M的N階本原單位根，滿足：

amn是a-mn在模M下的逆元，滿足以下性質：

NTT運算是一個遞推的過程，圖1給出了N=8點的NTT運算結構。如圖1中的橢圓標識所示，NTT變換后的結果順序與原輸入順序呈二進制的倒序關系，因此為避免在計算完成后進行順序變換，通常采用逆序的方式進行運算，運算結構如圖2所示。圖3為一次蝶形運算。N通常可以表示為2的冪的形式，N=2L，則N點NTT運算需要執行次蝶形運算，所以8點NTT需要執行12次蝶形運算。

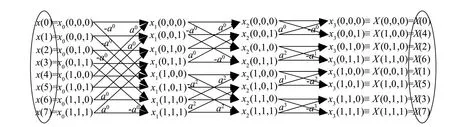
圖1 8點NTT運算結構

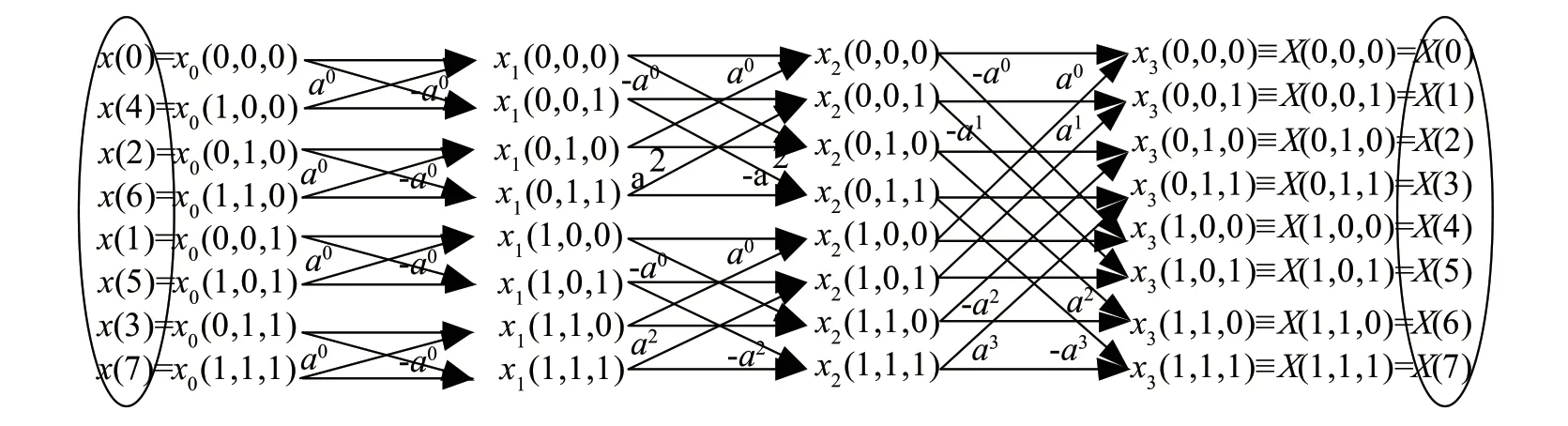
圖2 8點NTT逆序運算結構

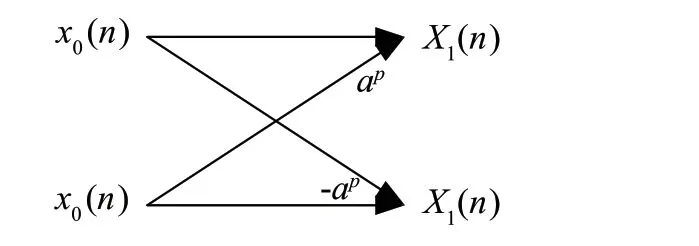
圖3 蝶形運算a

2 多項式乘法FPGA實現

2.1 多項式乘法算法

NTT中的每一次蝶形運算都需要做一次乘法和乘法結果取模運算，因此快速完成乘法和取模運算是提高NTT運算效率的關鍵。本文采用了Longa等人[9]提出的適用于模數M=k2p+1的高效取模算法，即LN取模算法，再結合FPGA內部的高效乘法器來實現NTT快速運算。

LN取模算法有K-RED和K-RED2x兩種形式[10]，如算法1和算法2所示。算法1適用于對加法結果取模，算法2適用于對乘法結果取模。

NTT變換和逆NTT變換算法如下：

算法3中M為模數，g為單位根，N為多項式的項數，如果N不滿足2的整數次冪需要補0。步驟6-9為一次蝶形運算。步驟11正變換查t1，逆變換查t2。

算法4中的步驟7每運算一次相當于在該項上乘以了k，步驟8每運算一次相當于在該項上乘以k2，如果對步驟8中每個gg都乘以k-1，經過步驟8運算后也相當于該項上乘以k。NTT每一項的運算次數為算法4中步驟2總的循環次數，即log2N次（N為多項式的項數）。所以每項都增加了klog2N倍，增加部分可以通過預計算的方式消除。

算法5中的步驟1是為了消除NNT運算時每項增加的klog2N倍而做的預處理。步驟6中的k-(4+log2N)N-1則是為了消除INNT運算后擴大的klog2N倍，并完成INNT運算后的除法運算。

2.2 多項式乘法FPGA實現

多項式乘法的FPGA實現如圖4所示。

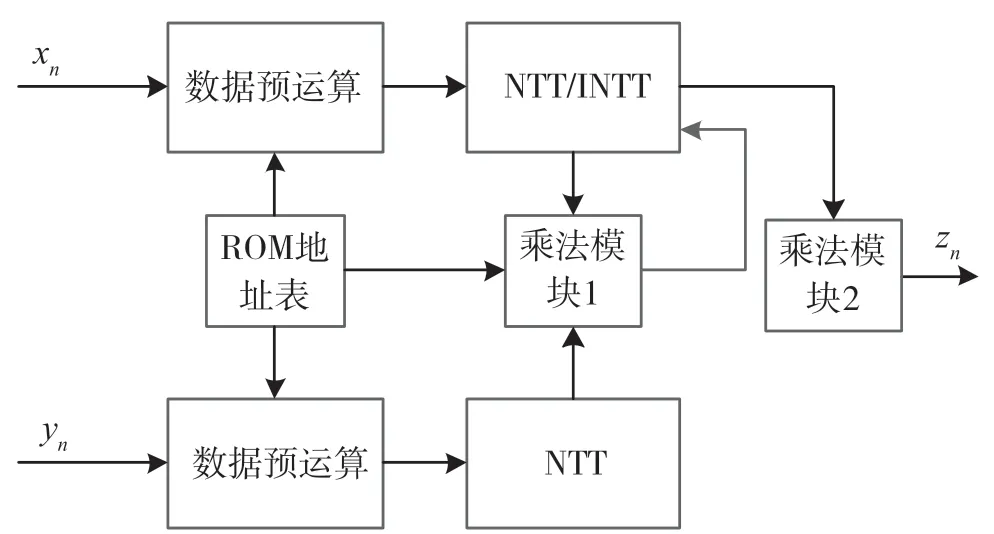
圖4 多項式乘法FPGA實現

2.2.1 數據預運算模塊

數據預運算模塊用于對多項式數據進行預處理，同時完成對多項式的倒位序。ROM地址表內存放預計算好的位序映射表。根據ROM讀出的地址讀取原始序列，預運算后寫入NTT模塊內的存儲器中。

2.2.2 NTT模塊

圖5為NTT模塊的實現。

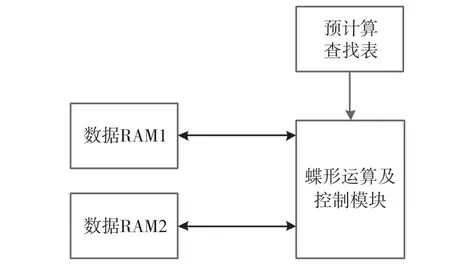
圖5 NTT實現

數據RAM1和數據RAM2為多項式系數存儲區，由于FPGA內部實現的RAM通常只有2路通道，不能滿足蝶形運算同時對RAM的2次讀和寫操作。為了解決這個問題，本文設計了RAM1和RAM2兩個數據存儲區。當RAM1作為數據讀取區時，蝶形運算的結果寫入RAM2區，當RAM2作為數據讀取區時，蝶形運算的結果寫入RAM1區，由內部控制模塊乒乓切換兩個數據區的讀寫模式。

預計算查找表用于存放蝶形運算所需的預計算數據，該數據可以預先計算好后固化在存儲區內部，不占用NTT的計算時間。預計算的數據包括k-1ai，k-1a-i，k-(2+log2N)和k-(4+log2N)N-1。

蝶形運算及控制模塊通過狀態機控制NTT的3層循環，以及每次蝶形數據和預計算數據的讀取，調用K-RED和K-RED2x完成運算。因蝶形運算下一次的輸入數據不會用到上一次的結果，所以蝶形運算可實現流水操作，從而提升運算性能。

2.2.3 乘法模塊

乘法模塊用于完成算法5的步驟4和步驟6。其中乘法模塊1用于完成兩個多項式轉換到NTT域后各項的相乘，并根據ROM地址表內存放的地址讀取多項式的值相乘，將結果存放在NNT的RAM內，用于逆NNT運算。乘法模塊2用于完成逆NTT運算結果除N運算和消除K-RED2x運算產生的k2縮放。由于k通常都不大，K-RED2x內部的k2x0和kx1可以轉換為由移位和加法實現，不需要乘法運算。

3 實現結果評估

為了便于結果評估，本文選用模數M=12 289，并設多項式的項數N=1 024，測試平臺采用Xilinx公司的XC7K325T型號FPGA。

Kuo等人[11]運用了適合于硬件實現的模約減方法，但使用了較多的加法器，編譯頻率不高。Oder等人[12]使用的模約減模塊包含延時較大的關鍵路徑，且存取效率不高，編譯頻率也較低。本文的蝶形運算模塊及LN模運算模塊均采用流水線實現，所以實現頻率較高，達到了320 MHz。由于采用流水實現，預算模塊和NTT運算可以并行執行，且NTT內部的蝶形運算模塊同樣為流水結構，從而大大提高了運算性能。表1為本文多項式乘法硬件實現與現有一些硬件實現的比較結果。其中，查找表（Look-Up-Table，LUT）、寄存器（REGister，REG）、塊存儲器（Block RAM，BRAM）和乘法器（Digital Signal Processing，DSP）分別為FPGA內硬件資源。

表1 多項式乘法硬件評估結果

4 結語

本文提出的多項式乘法硬件實現方法，采用不完全模約減的方式取模，大大減少了取模的時間。同時采用了乒乓切換、流水技術和雙NTT模塊架構，一方面提高了存儲器讀寫帶寬，另一方面減少了運算過程中的等待時間，從而提升了運算性能。此外，由于采用了流水設計，編譯主頻也較高，達到了320 MHz。因此，本設計無論是在資源占用方面還是在處理性能方面都具有一定的優勢，對基于格的后量子密碼的硬件實現具有一定的參考意義。