模袋混凝土干濕-凍融侵蝕孔結構的分形特征

孫浩然， 鄒春霞，*， 薛慧君， 趙 泉， 武 軍

（1.內蒙古農業大學 水利與土木建筑工程學院，內蒙古 呼和浩特 010018；2.內蒙古河套灌區烏拉特灌域管理局，內蒙古 巴彥淖爾 014400）

內蒙古河套灌區模袋混凝土襯砌常因季節性凍融和干濕交替而引起局部和大面積開裂、破壞等問題，嚴重影響其使用壽命和渠系建筑物的輸水效率.研究發現，干濕-凍融耦合作用所致混凝土表面開裂、破壞等情況比單純的凍融或干濕作用更為嚴重.當混凝土的相對動彈性模量達到相同的損傷度時，干濕-凍融耦合下損傷速率最快［1］.這種損傷關系不是兩者的簡單疊加，而是一種超疊加效應關系，與混凝土組成和結構特征、干濕-凍融循環制度等因素有關.混凝土材料是一種具有復雜結構的復合材料體系，孔隙結構對其耐久性有著重要影響.將掃描電鏡（SEM）和核磁共振（NMR）技術應用在混凝土工程中，有助于獲得混凝土微觀結構特征，為深入研究混凝土損傷情況提供了一種有效途徑.而如何定量描述干濕-凍融耦合作用下的孔隙狀態變化規律是研究模袋混凝土耐久性能亟待解決的問題.

分形理論作為研究物質不規則性和復雜現象的學科，與混凝土內部復雜的孔隙結構變化具有良好的契合性.近年來，許多學者嘗試應用分形理論來研究混凝土孔結構變化.余志龍等［2］應用SEM 研究發現分形維數能夠表征混凝土的微觀結構；樊水龍［3］研究了在干濕循環下蝕變花崗巖的損傷程度與分形維數之間的關系，通過分形理論將SEM 圖像從定性分析變為定量描述.張超謨等［4］進行了基于核磁共振T2譜分布的儲層巖石孔隙分形結構的研究.Jin 等［5］基于分形理論發現氣泡分布對混凝土抗凍性有重要影響.分形理論在混凝土工程中的應用顯示出分形維數具有表征混凝土孔隙結構變化的能力.

本文總結前人的研究成果，將分形維數作為固定參數構建模袋混凝土干濕-凍融損傷模型.以分形維數的方法表征其內部損傷，探究不同維度下分形維數間的關聯性.基于Coates 模型［6］，計算出混凝土孔隙度、滲透率與分形維數間的數學關系.結合小波變換的回歸估計，得到相對動彈性模量與滲透率的回歸方程，提出以相對動彈性模量和分形維數為損傷指標的干濕-凍融損傷模型.

1 試驗

1.1 試驗材料

水泥采用蒙西P·O 42.5R 硅酸鹽水泥；細骨料和粗骨料均取自巴彥淖爾市烏拉特前旗九公里料場；粉煤灰采用包頭電廠的Ⅱ級粉煤灰；硅粉采用巴彥淖爾市烏拉特前旗玉石加工廠的固體廢棄料，經研磨處理后滿足混凝土試驗要求；外加劑采用YE-NGX 萘系高效減水劑；拌和水采用普通自來水；干濕-凍融循環用水取自巴彥淖爾市烏拉特前旗的黃河水.模袋混凝土的配合比見表1.

表1 模袋混凝土的配合比Table 1 Mix proportion of mold-bag concrete kg/m3

1.2 試驗方法

干濕-凍融循環試驗試件為標準養護后的100 mm×100 mm×400 mm 棱柱體.根據內蒙古河套灌區氣候特征和農業灌溉規律，選擇干濕-凍融循環制度為5 次干濕循環、25 次凍融循環為1 次干濕-凍融循環.首先，將試件放入（55±5）℃烘箱中烘干11 h 后冷卻1 h，然后置于黃河水中浸泡12 h 為1個干濕循環.5 次干濕循環后，將試塊放入快速凍融機中進行25 次凍融循環，此為1 個干濕-凍融循環.重復做8 次干濕-凍融循環，每次干濕-凍融循環結束后測量試件的相對動彈性模量.分別在0、3、5、8 次干濕-凍融循環結束時，測定混凝土微觀結構形貌和孔隙特征.采用S-4800 型掃描電子顯微鏡觀測試件微觀結構形貌，不同干濕-凍融循環次數（n）的SEM樣品取自模袋混凝土內部的同一位置. 采用MesoMR23-60 型核磁共振儀分析混凝土孔隙特征，用金剛鉆取芯機鉆芯取樣，尺寸為φ48×50 mm，真空飽水后開展核磁共振試驗.

2 理論方法

2.1 SEM 分形維數計算方法

通過SEM 得到模袋混凝土干濕-凍融的微觀圖像，一方面可以直接觀察其表面的結構和形態特征，另一方面可以利用分形維數將定性描述轉為定量分析，以便揭示其損傷演變規律.計算圖像分形維數的方法較多，如差分盒維數法、灰度插值法、雙毯法等［7-8］.本研究選擇差分盒維數法對經歷不同干濕-凍融循環次數試件的SEM 圖像進行分形分析.運用Matlab軟件計算SEM圖像的分形維數，首先運用Otus法［9］計算出圖像的最佳閾值，然后對圖像進行二值化處理，將圖像轉化為只含有0和1的矩陣.SEM圖像的像素尺寸逐漸減小，其對應的盒子累積個數相應增加.當盒子邊長ε趨于0時，理論上盒子個數N（ε）趨于無窮.對ε和N（ε）分別取對數，求出lnN（ε）對lnε的斜率，其斜率的負值便是該分形圖像的計盒維數DS，計算式如下［10］：

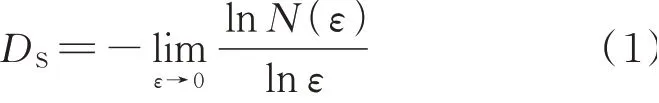
2.2 NMR 分形維數計算方法

通過NMR 得到模袋混凝土的微觀孔隙結構特征，針對其特征參數計算得到的分形維數可定量反映孔隙結構狀態.本研究根據NMR 的T2譜曲線特點推導出分形維數算法，并依據該算法分析不同孔隙結構的分形特征.混凝土中孔隙數目N滿足下式［11］：

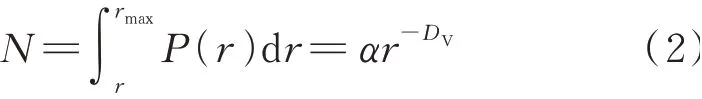
式中：r為孔隙半徑；rmax為孔隙半徑最大值；P（r）為孔隙分布密度函數；α為修正因子；DV為孔隙體積的分形維數.

此時核磁共振T2譜的分形算式為：

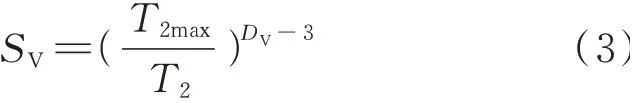
式中：T2為弛豫時間；T2max為最大弛豫時間；SV為橫向弛豫時間小于T2時孔隙累積體積占總孔隙體積的比值.

將式（3）兩邊取對數得到近似分形幾何算式：

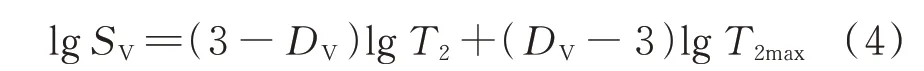
2.3 基于小波變換的回歸估計方法

回歸估計是在2組隨機變量中找出關聯，因此不存在理想的、均勻分布的變量空間.在大多數情況下需要對這種關聯形式進行假定，即建立回歸模型.小波變換能夠對時間（空間）頻率進行局部化，通過伸縮平移運算對信號逐步進行多尺度細化，最終達到高頻處時間細分、低頻處頻率細分的能自動適應時頻信號分析的要求.

3 結果與討論

3.1 SEM 微觀結構形貌的分形特性

模袋混凝土的SEM 圖見圖1.由圖1 可見：干濕-凍融循環前試件微觀結構呈鱗片狀，存在部分不均勻孔隙結構，但過渡較為均勻，此時有水化產物生成；隨著干濕-凍融循環次數n的增加，混凝土表面鱗片消失，團絮狀的粉煤灰受黃河水中硫酸根離子侵蝕也逐漸消失，混凝土發生纖維化，表面由平整變得不平整，裂隙增多；特別是在干濕-凍融循環8 次后，纖維狀產物變細，局部發生斷裂，表明干濕-凍融循環對模袋混凝土造成不可逆的損傷.纖維狀產物經能譜（EDS）分析（見圖2）發現含有Ca、Fe、Al和Si等元素，證明該產物是鈣礬石（AFt）［12］.進一步，通過X射線衍射（XRD）分析（見圖3）發現其主要成分為水化硅酸鈣（C-S-H）凝膠、SiO2和AFt.

圖1 模袋混凝土的SEM 圖Fig.1 SEM micrographs of mold-bag concrete

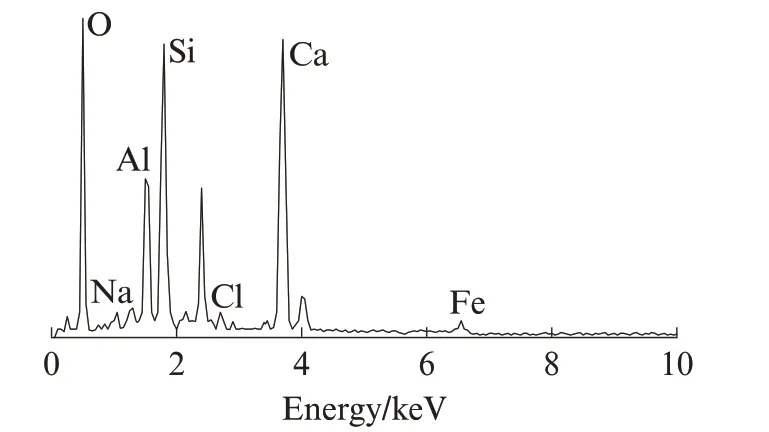
圖2 纖維狀產物的EDS 圖譜Fig.2 EDS spectrum of fibrous products

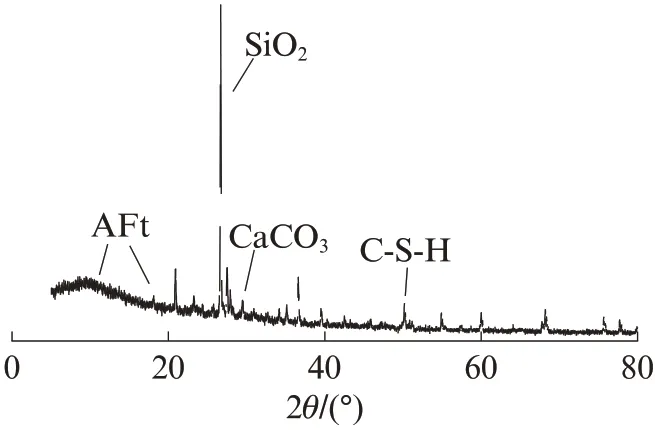
圖3 纖維狀產物的XRD 圖譜Fig.3 XRD pattern of fibrous products

模袋混凝土的SEM 二值化圖像見圖4.利用圖4得到二值化閾值及分形維數DS，結果見表2.由表2可見：SEM 圖像的分形維數精度R2較高，能夠較好地反映圖像的非線性程度.

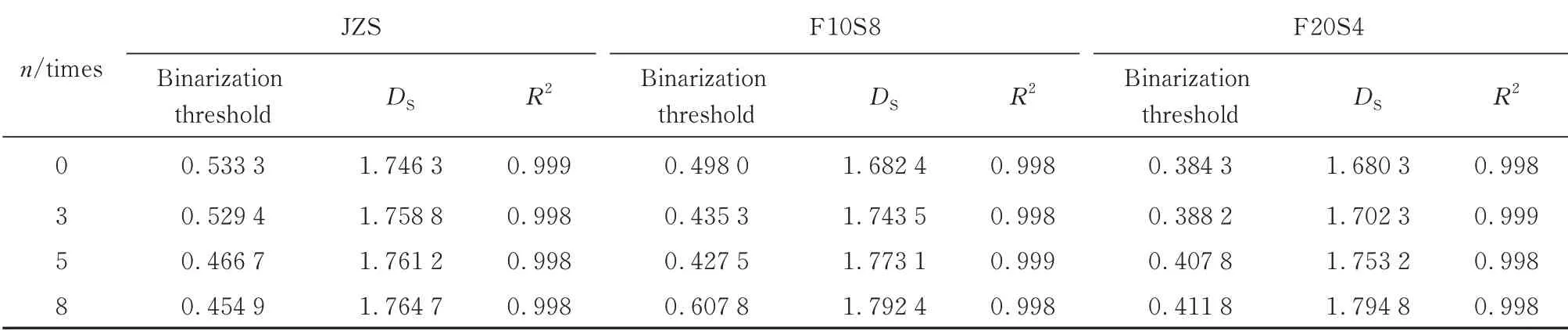
表2 SEM 二值化圖像的分形維數結果Table 2 Results of fractal dimension from SEM binary images

圖4 模袋混凝土的SEM 二值化圖像Fig.4 SEM binary images of mold-bag concrete

對SEM 圖中反映的損傷特征進一步定量分析，干濕-凍融循環8 次后部分纖維狀產物發生斷裂，分形維數隨之增大.干濕-凍融循環作用后模袋混凝土的微觀維數發生了變化，即分形維數隨著干濕-凍融循環次數的不斷增加而規律性增大.分形維數增大定量地表征了模袋混凝土內部裂隙、孔隙、構造層理等不規則性受干濕-凍融侵蝕作用趨于復雜化，混凝土損傷加重，耐久性能下降.同時，不同配合比模袋混凝土經歷干濕-凍融循環作用后，其分形維數增加幅度和速度與其組成成分和內部結構有關.

3.2 模袋混凝土的孔隙結構及其分形特征

3.2.1 核磁共振孔隙結構

核磁共振試驗可得到干濕-凍融循環作用下模袋混凝土的孔隙結構變化，T2譜圖像中的弛豫時間與孔隙半徑呈正相關，孔隙數量與峰面積相關.T2譜弛豫時間越長，則孔隙半徑越大，孔隙水自由度越大，束縛流體飽和度越小，反之相反［13］.弛豫時間和孔隙參數的關系可利用下式表示：

式中：ρ為與材料性質有關的弛豫強度；S為孔隙的表面積；V為孔隙體積.

根據核磁共振T2譜計算孔隙半徑，將模袋混凝土的孔徑劃分為＜0.1 μm、0.1～1 μm、1～10 μm、＞10 μm 這4 個部分，試件JZS、F10S8、F20S4 各區間的孔隙分布如圖5 所示.從圖5 可以看出：隨著干濕-凍融循環次數的增加，微孔呈增多趨勢；0.1～1 μm 孔隙逐漸增多；而1～10 μm 孔隙逐漸減少；試件F20S4干濕-凍融循環8 次后，在大孔區間（＞10 μm）內首次出現第3 個波峰.

3.2.2 基于NMR 技術的分形維數

將核磁共振T2譜對應的孔隙半徑作為試驗數據來計算孔隙體積的分形維數.在式（4）中，橫向弛豫時間T2譜雙曲線存在2 個不同的直線階段.因此可由式（4）的斜率求得小于臨界弛豫時間的分形維數DVmin和大于臨界弛豫時間的分形維數DVmax，結果如表3 所示.

孔隙結構分布決定核磁共振分形維數的大小［14］.混凝土中微孔大多與比表面積相關，而中孔、大孔更多與孔隙體積相關.從圖5 和表3 可以看出，與孔隙體積呈更多相關性的中孔、大孔分形維數逐漸增加.孔隙水結冰融化的過程，相當于對孔壁不斷地加荷卸荷.混凝土內部的微孔逐漸增多且部分孔隙轉變為大孔隙，大孔隙內部大多為重力水，凍結過程中率先結冰，使滲透壓力和靜水壓力的凍脹作用逐漸加大［15］.中孔、大孔分形維數的變化，反映了干濕-凍融循環作用下模袋混凝土內部的損傷過程.圖6 為歐式幾何變換后不同維度下的分形維數.由圖6 可見，經變換后SEM 圖像的分形維數與核磁共振的分形維數相差不大，最大相差1.2%，平均差距為0.8%.說明不同維度下的分形維數具有一定的關聯性.

圖5 試件JZS、F10S8、F20S4 各區間孔隙分布Fig.5 Pore distribution in different intervals of JZS，F10S8，F20S4 specimens

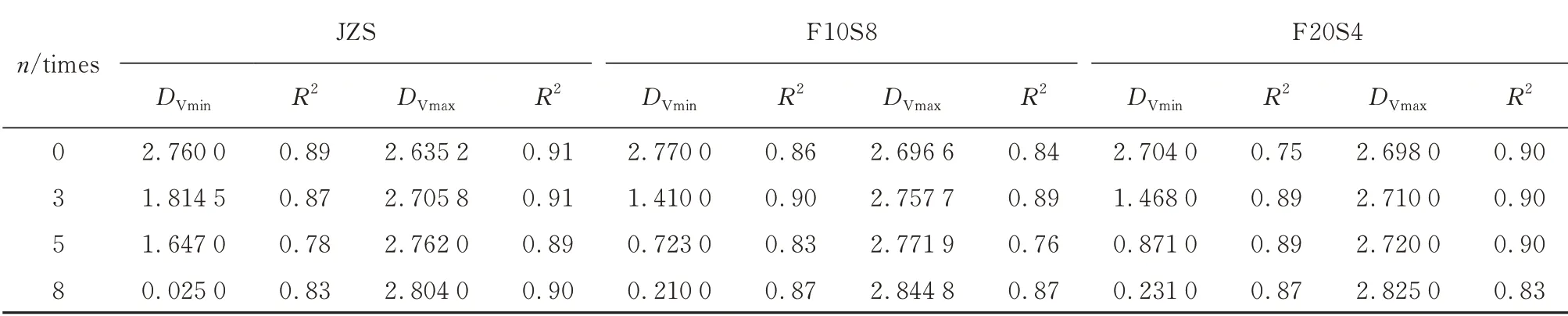
表3 基于核磁共振（NMR）計算的分形維數Table 3 Fractal dimension calculated based on nuclear magnetic resonance method

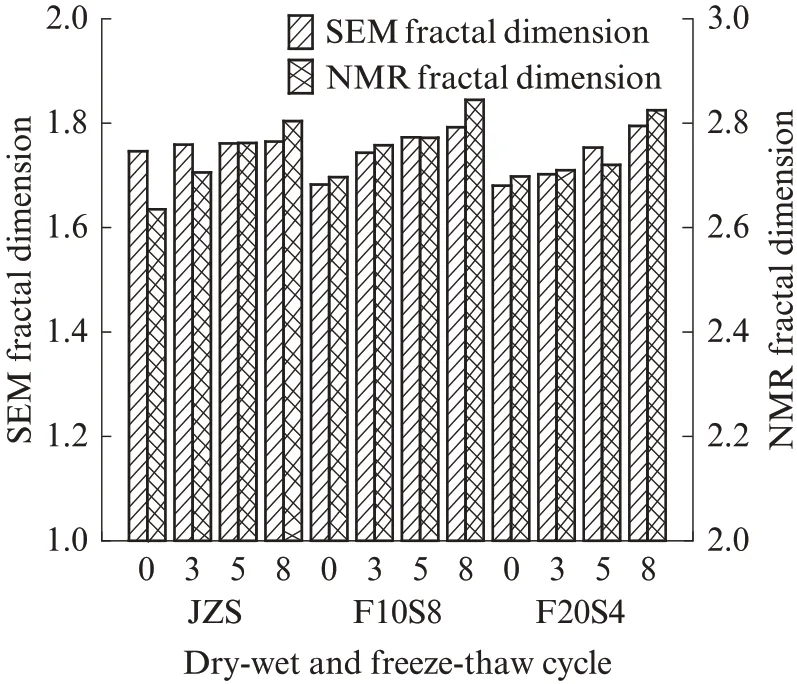
圖6 不同維度下的分形維數Fig.6 Fractal dimension in different dimensions

3.3 體積孔隙度、滲透率與分形維數間的關系

歐式幾何中n維物體在截面上相交為n-1 維，將歐式幾何應用到分形幾何中，分形體與截面相交，相交后分形體減小1 維.以DL、DS、DV分別從截線、平面、空間上表示分形體的維數，得到了分形維數表示的截線、平面、空間的數學關系［16］：

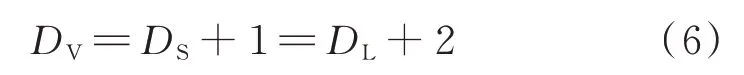
根據式（1）、（4）及面孔隙度、體積孔隙度的物理意義，得到分形維數與面孔隙度及體積孔隙度之間的關系：

式中：τ為體積孔隙度；R為差維因子，利用試驗數據回歸擬合后得到R=1.05；ω為面孔隙度，等于SEM圖像內孔隙面積與檢測平面面積的比值.

采用Coates 模型［6］計算與混凝土水飽和度、孔隙度相關的混凝土滲透率：

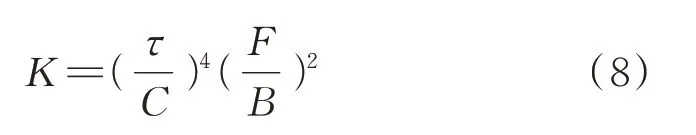
式中：K為滲透率；C為調整系數；F為自由水飽和度；B為束縛水飽和度.

將式（7）代入式（8），得到滲透率與分形維數、面孔隙度、水飽和度的關系：

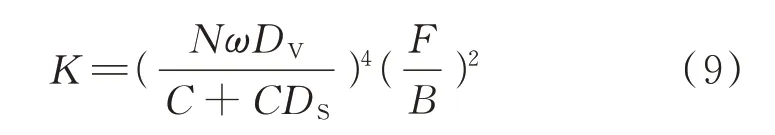
將試驗所得混凝土水飽和度、分形維數等數據分別代入式（7）、（9），計算出混凝土的體積孔隙度和滲透率，計算值與實測值的比較見表4、5.

表4、5 顯示，基于分形維數得到的體積孔隙度和滲透率計算值與實測值相差不大，誤差均在6%左右，說明所建立的分形維數與混凝土體積孔隙度和滲透率的數學模型是合理的.

表4 體積孔隙度計算值與實測值的比較Table 4 Comparison of calculated and measured volume porosity%

表5 滲透率計算值與實測值的比較Table 5 Comparison of calculated and measured permeability μm2

3.4 基于小波變換的回歸估計

本研究選擇干濕-凍融循環下模袋混凝土的相對動彈性模量和滲透率進行回歸估計.借助Matlab軟件的小波工具對相對動彈性模量所對應的滲透率進行小波分解，分解水平（level）為3，進行4 層分解，得到細節系數和近似函數.細節系數包含了試驗過程中由于噪聲或儀器本身引起的誤差.試驗測得的模袋混凝土相對動彈性模量見表6.

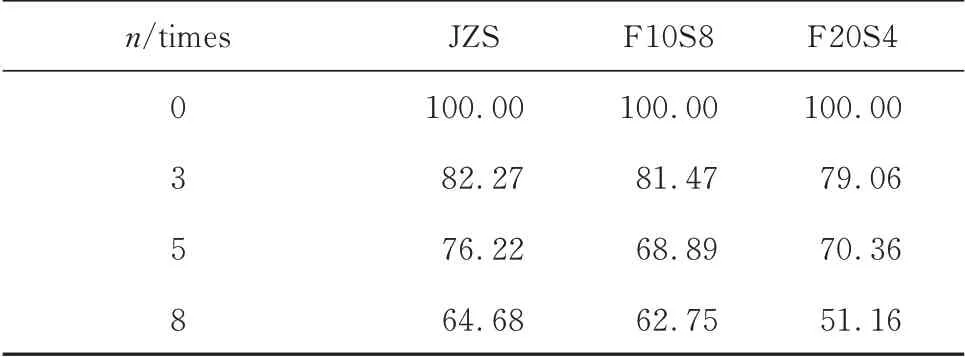
表6 模袋混凝土相對動彈性模量Table 6 Relative dynamic elastic modulus of mold-bag concrete%

依據近似函數，建立基于小波變換的回歸方程：

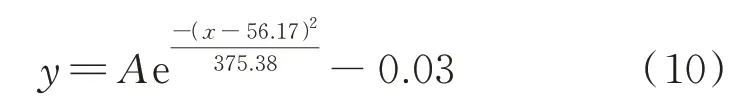
式中：y為滲透率；x為相對動彈性模量；A為相關系數.

將式（9）代入式（10），得到相對動彈性模量和分形維數、飽和度之間的關系：

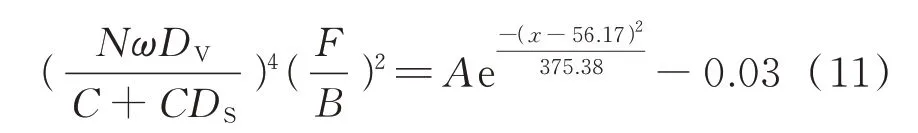
將基于小波變換回歸估計建立的相對動彈性模量與滲透率的回歸方程（式（11））和試驗結果進行比較，如圖7 所示.由圖7 可見，該回歸方程與試驗結果基本吻合，說明依據分形理論，以相對動彈性模量為損傷指標建立的干濕-凍融損傷模型是合理的.

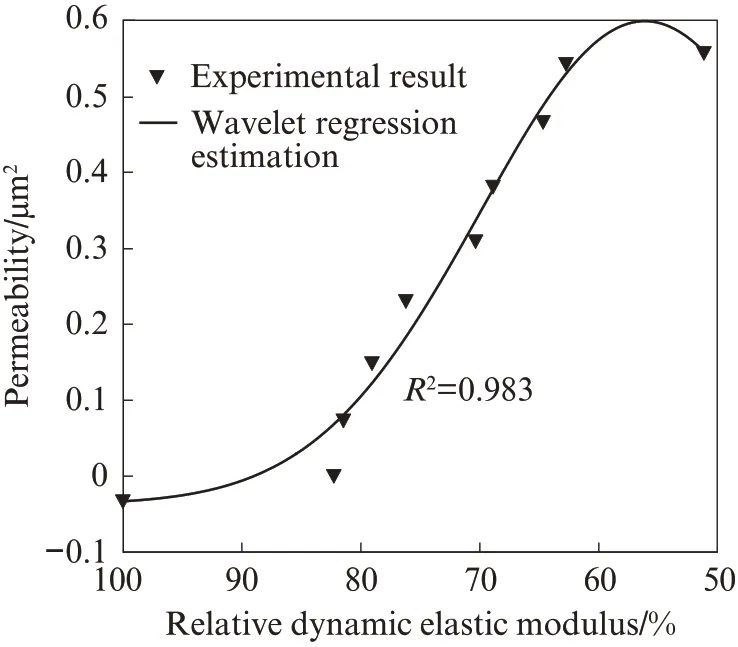
圖7 回歸方程與試驗結果對比Fig.7 Comparison between regression equation and experimental results

4 結論

（1）分形維數可以定量描述不同干濕-凍融循環次數下模袋混凝土的微觀損傷情況.結合掃描電鏡和核磁共振試驗結果，分形維數隨著模袋混凝土干濕-凍融循環次數的增加而增大，表明模袋混凝土的損傷程度體現為分形維數的增大.

（2）基于核磁共振T2譜，建立了橫向弛豫時間的分形公式，根據T2譜分布特征計算出的分形維數DV能夠表征干濕-凍融循環下模袋混凝土內部孔隙的演變規律.并將不同維度下的分形維數通過歐式幾何的概念建立聯系，發現掃描電鏡下二維圖像的分形維數與核磁共振下三維孔隙結構的分析維數具有很高的關聯性，其平均差距為0.8%.

（3）利用分形理論將不同試驗結果聯系起來，建立了模袋混凝土體積孔隙度、滲透率與分形維數的數學關系，計算值與試驗結果基本吻合，可以預測混凝土的孔隙度和滲透率.

（4）引入小波變換的回歸估計，建立了相對動彈性模量與滲透率的回歸方程，推導出以分形理論為基礎的損傷模型，為深入研究模袋混凝土干濕-凍融損傷機理奠定了基礎.