烴同分異構體的計數

馬騁遠，李啟翔

上海外國語大學附屬外國語學校，上海 200083

同分異構現象是有機化學中的重要現象，也是高中化學學習的重點。在高二學年的化學公開課“從‘烴’出發、走進科研——認識碳氫化合物的多樣性”當中，作者所在小組在老師的指導下對于青蒿素提取產物當中的同分異構現象進行了探究，并對同分異構現象的復雜產生了直觀的認識。本文作者在課外愛好數學與信息學，故在課后對于如何嚴謹系統地對于復雜有機物的同分異構體進行精確計數產生了興趣。本探究因此產生。

高中的化學教學中已經教授了對于較簡單有機物同分異構體較為系統的枚舉方法。例如，可以通過枚舉最長碳鏈的長度以及官能團的位置，結合對等價碳原子以及對稱性的討論較有條理地枚舉烴及其衍生物的同分異構體。然而，以上枚舉的工作量正比于同分異構體的數目，因此對于碳原子較多的烴(例如辛烷及以上)難以應用。然而其中的若干步驟，如“枚舉最長鏈”“討論對稱性”對于通用的計數算法仍然有相當的借鑒意義。

查閱文獻可知，對于化學結構同分異構體的枚舉計數有漫長的研究歷史。在1875年，Cayley便嘗試推導烷烴同分異構體的計數公式(不計立體異構)并正確計算了碳原子數為1至11時的答案[1]。Pólya于1937年提出了具有里程碑意義的Pólya計數定理并結合圖論推導了烷烴、烷基、一元醇等有機物的同分異構體數[2,3]。Rains與Sloane運用Pólya的成果修正拓展了Cayley的計數公式[4]。除此以外，Herrman、Henze、Blaire、Read等也對烷烴同分異構體的計數進行過研究[5–7]。Robinson等進一步研究了考慮手性異構的同分異構體計數[8]。

雖然有機物同分異構體的計數已有大量成果涌現，但其成果多為外語且閱讀所需的數學門檻高；國內雖也有相似的研究[9,10]，但其結果的形式復雜，推導的過程簡略，理解難度大。因此本探究的一個主要目標便是盡可能地在高中化學與數學知識的基礎上，采用盡可能簡潔可推廣的方法對于一部分烴類的同分異構體進行計數，從而達成更低的閱讀門檻與理解難度。對于與作者同齡的高中讀者，作者相信本探究能夠提供一個看待同分異構現象的特殊視角，對于加深課內所學的同分異構現象的理解應當是不無裨益的。

我們在節1介紹本文將要運用的數學工具，在節2中運用這些數學工具對烷烴、烷基、一烯烴、一炔烴、苯的衍生物、二取代烷烴以及二烯烴的同分異構體計數進行簡明的、系統化的推導。在節3中我們將稍作拓展，探索同分異構體計數的漸進特征與近似公式。在同分異構體的精確計數上，本文沿用Cayley，Rains與Sloane的思路[1,4]，但繞過對于圖論的依賴；然而，本文所使用的Pólya計數定理所依賴的部分抽象代數背景是無法避免的，為此，本文在補充材料中簡明地附上了所有相關定義、引理與證明，力求自洽。

本文的所有推導皆基于如下假設：

· 所有碳成四鍵、氫成一鍵的結構式對應的有機物都現實存在。

· 碳鏈相同的兩有機物結構相同，即只考慮碳鏈異構，不考慮立體異構。

· 如不特殊說明，則所有本文涉及到的所有烴無環(苯環除外)。

前兩假設在高中階段的化學學習當中往往都是默認成立的。對于假設3，我們在節4中設想了一類處理單環烷烴的方案，但因為和苯的衍生物的處理方式相似并未詳細展開，有興趣的讀者可以自行探究。

最后，需要指出的是，本文的科普性強于實用性。相對于部分參考文獻，本文推導的方式可能較為復雜，探討情形也較為簡單，然而這是符合筆者意圖的。筆者身為高中生，在初學同分異構體計數時就對精確計數的方法產生好奇，然而也曾在數次嘗試中因接觸大量的超綱的定理公式對此望而生畏，和其他同學一樣對這一問題的難度產生了過高的假設。在高三借課程機會認真梳理后，方才發覺這一問題實際上并非高中生力所不能及，而推導的過程也為理解化合物的結構提供了一種抽象的、遞歸的特殊視角，也應用了計算思維。筆者原先作本文的目的是記錄并與同學們分享交流，在李啟翔老師的建議與支持下才嘗試修改投稿，如有不合規范之處，還望讀者包涵。

1 數學工具

在開始正式推導之前，我們簡要介紹本文后文會經常用到的數學工具——生成函數以及Pólya計數定理[3]。

1.1 生成函數

定義1 (生成函數)：對于無窮數列{a0,a1,a2, …}，定義其生成函數為以該數列為系數的形式冪級數(多項式)：

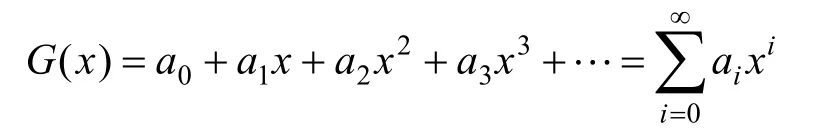
生成函數并不是真正意義上的函數，不用于帶入求值，而只是表示無窮數列的一種方式。例如，含0, 1, 2, 3, …個碳原子的烷烴的同分異構體的個數即構成一個無窮數列。在本文中，生成函數主要用來表達與前例類似的，以原子個數為下標的“結構數”或“方案數”。

以下舉例說明生成函數的若干性質：假設i個原子可以組成ai種結構A，對應生成函數為A(x)；j個原子可以組成bj種結構B，對應生成函數為B(x)，則：

1) 去掉2個原子，用剩下的原子組成結構A的方案數{0, 0,a0,a1,a2, …}對應的生成函數是x2A(x)。

2) 組成兩個相同的結構A的方案數{a0, 0,a1, 0,a2, 0…}對應的生成函數是A(x2)。

3) 要么組成結構A，要么組成結構B的方案數{an+bn}對應的生成函數是A(x) +B(x)。

4) 用一些原子組成結構A，另一些原子組成結構B的方案數對應的生成函數就是A(x)B(x)。

可以看到，生成函數的形式允許我們簡化數列的操作與表示。

1.2 Pólya計數定理

考查下列計數問題：假設若干原子可以組成某類結構。更具體地，n個原子可以組成fn種不同的結構(設生成函數f(x))。在此基礎上，如何計算共n個原子分組構成k個子結構的總方案數？

若組成的k個子結構是有序的，則由上一節關于生成函數的簡介，方法數的生成函數即為fk(x)。

但是若不計順序，則必須在fk(x)的基礎上進行類似排列數到組合數的“去序”過程。我們注意到兩個“有序方案”在無序的背景下“等價/本質相同”當且僅當兩個方案可以通過重新排列k個結構互相轉化，且這種等價關系是具有傳遞性的。假設F是所有有序方案的集合，所求答案就是這個集合中不同等價類的個數。引入抽象代數的語言：所求答案為F在置換群Sk(見補充材料定義9)作用(見補充材料定義10)下的軌道(見補充材料定義11)數。

依據Burnside引理(證明見補充材料定理3)，一個集合在一個置換群作用下的軌道數等于群內各置換不動點個數的平均值。考慮對于一個置換π如何計算不動點個數(的生成函數)。設置換π可以分解為若干個環，其中大小為i的有ci個。由不動點的定義，每個i元環內的i個元素必須相同。在我們的問題中，一個元素對應一個結構。注意到，將n個原子分組組合為i個相同結構的方案數可以用生成函數f(xi)表示。因此，由乘法原理，置換π下的不動點個數即可表示為如下生成函數：

結合Burnside引理，所有有序方案在Sk作用下的軌道數，即所求答案，可以用如下生成函數表示：

該結論被稱為Pólya計數定理。

以下給出k= 2, 3, 4時的Sk的表達式

2 同分異構體計數

在簡要介紹了本文所使用的數學工具后，我們在本節正式推導部分烴類同分異構體的計數方法。

2.1 烷基的同分異構體計數

在所有烴類中，烷基的同分異構體的計數是最為簡單的。主要原因有二：

1) 烷基中所有的碳都成四根單鍵。

2) 烷基當中成半鍵的碳原子有特殊性(下文不妨稱其為“根碳原子”)，使其可以成為計數的基準點。

結合特性，烷基的化學結構便具有遞歸性。更具體地說，若將-H視作0-烷基，那么所有至少有一個碳原子的烷基便拆分為根碳原子以及三個更小的烷基。圖1以乙基為例展示了這種遞歸性。

圖1 烷基結構的遞歸性

如果設烷基的同分異構體個數的生成函數為T(x)。那么由生成函數的性質以及Pólya計數定理，我們便可以寫出關于T(x)的方程：

方程(4)并不能讓我們顯式地求出T(x)的表達式。然而，方程(4)的形式啟發我們使用遞推的方式對T(x)進行逼近。

定義2 (烷基的高)：定義一個烷基的高為包括根碳原子在內，從根碳原子到最遠的氫原子所要經過的碳原子數。例如甲基的高為1，乙基和異丙基的高為2，正丙基的高為3。

基于此定義，設Th(x)是高至多為h的烷基同分異構體數目的生成函數。由圖1，高h+ 1的烷基會被“分解”為3個高至多為h的烷基。因此，仿照方程(4)，我們可以寫出Th(x)的遞推式：

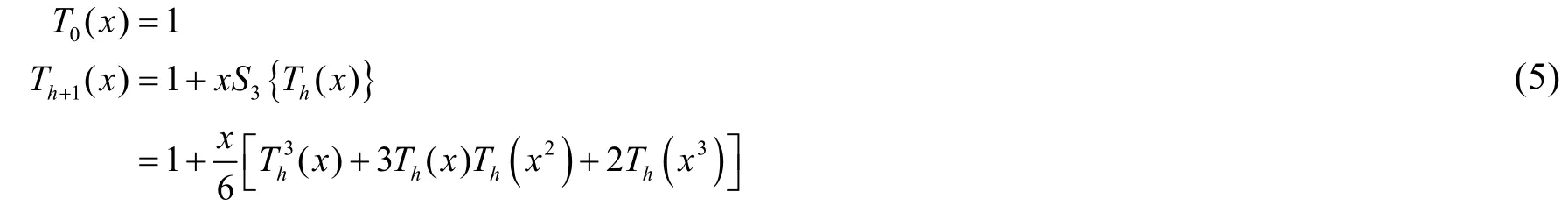
迭代若干次的結果如下：

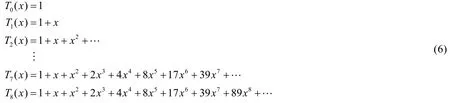
我們所求取的烷基同分異構體的個數便蘊含在Th(x)的系數中：―CH3有1種同分異構體、―C3H7有2種同分異構體、―C6H13有17種同分異構體、―C8H17有89種同分異構體……在只考慮碳鏈異構的情況下，我們的結果和常識是相符的。

在計算的過程中應當注意，由于方程(6)中包含立方項，因此每遞推一次，Th(x)的次數就增加到原來的3倍。為了避免指數增長給計算帶來的負擔，可以選擇在遞推時將Th(x)截斷至xh項。由于至多h個碳原子的烷基的高至多為h，因此截斷后的Th(x)的系數仍然正確表示了1至h個碳原子的烷基的同分異構體數目。

對于偏好非生成函數形式的讀者，我們根據方程(6)亦可給出烷基同分異構體數目的常規形式：設高至多為h的由n個碳原子組成的烷基的數目為th,n，則有：

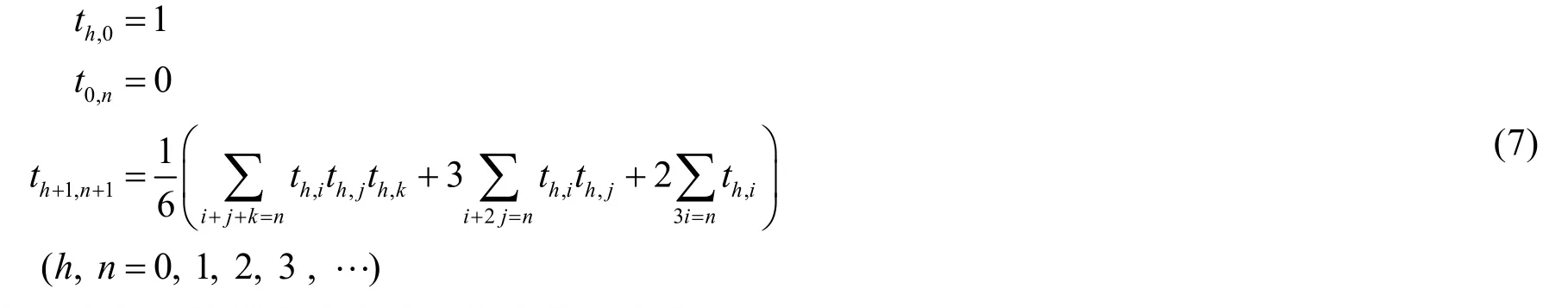
這個形式和文獻[10]中給出的遞推式是一致的。

我們同時注意到，由于烷烴的一鹵代物、一元醇、一元醛、一元羧酸等可以視為對應官能團和一個烷基組合而成，因此，本小節推導的烷基的同分異構體計數方法可直接應用于這些化合物的同分異構體計數。

2.2 烷烴的同分異構體計數

在成功推導烷基的同分異構體技術的基礎之上，我們考查烷烴的同分異構體計數。后者較前者更為復雜，因為烷烴當中并不自然存在類似烷基“根碳原子”的必然唯一存在且特殊的原子作為計數的基準點——而以上條件是在如此復雜結構的計數問題中避免重復計數的最重要途徑。

能否人工定義一個烷烴的“中心”為類似“根碳原子”的基準點？為了嚴謹化我們的洞見，我們作出如下定義：

定義3 (烷烴的直徑)：在烷烴中，任意兩氫原子被且僅被一條碳鏈連接。定義連接兩氫原子的最長碳鏈為烷烴的直徑，該碳鏈的長為烷烴的直徑長。

定義4 (烷烴的中心)：定義烷烴直徑中點處的碳原子(對)為烷烴的中心。

注：通過反證法易證，無論成單亦或成對，一個烷烴的中心可以被唯一確定。

為更直觀地說明定義，圖2展示了直徑長為偶數與奇數的復雜烷烴的直徑與中心。

圖2 復雜烷烴的直徑與中心

不妨設直徑長為d的烷烴數目的生成函數為Cd(x)。

由于烷烴中心的形態取決于其直徑長的奇偶性，其Cd(x)推導在兩種情況下自然有所不同，需要分類討論。

2.2.1 偶數直徑

觀察到，直徑長為2h的烷烴可以從其中心拆分為兩個分別以中心為根碳原子的，高為h的烷基，如圖3。

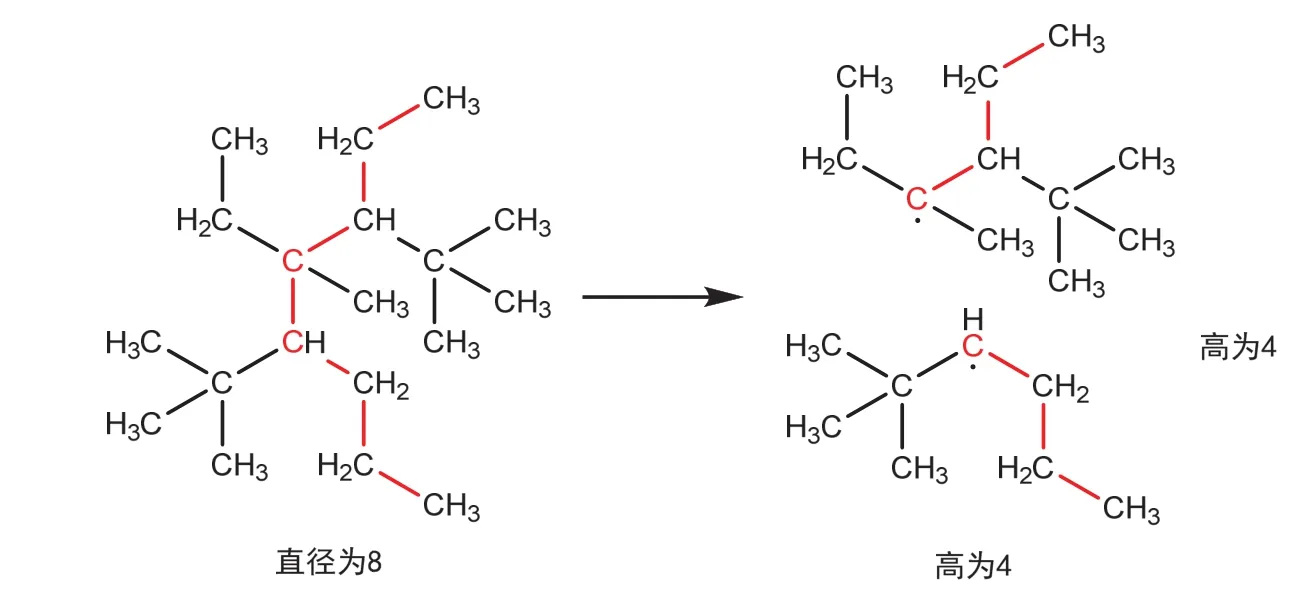
圖3 偶數直徑長烷烴的拆分

因為高恰為h的烷基的同分異構體數目的生成函數為因此便有：

2.2.2 奇數直徑

直徑長為2h+ 1的烷烴可以分拆為一個中心以及四個高至多為h的烷基，其中兩個高恰為h，如圖4所示。

圖4 奇數直徑長烷烴的拆分

我們使用排除法對于如此拆分的生成函數進行計算。四個高至多為h的烷基數目的生成函數是除去四個高至多為h? 1的情形對應的生成函數就是四個高至多為h，且至少有一個高恰好為h的烷基數目的生成函數。

在此基礎之上我們再減去恰有一個高恰為h的烷基的情形，即其余三個烷基的高度至多為h? 1，其對應的生成函數為最后，考慮到烷烴的中心也是一個碳原子，我們便得出了直徑長為奇數的烷烴同分異構體數目的生成函數：

最后，烷烴同分異構體數目的生成函數自然是不同直徑長對應的生成函數之和：

意義即為：甲、乙、丙烷的同分異構體有1種；丁烷2種；戊烷3種；己烷5種；庚烷9種；辛烷18種…這和手工枚舉的結果一致。

2.3 一烯烴的同分異構體計數

一烯烴雙鍵連接的兩個碳原子分別成兩根鍵，連接兩個烷基(包括氫原子)，在結構中具有特殊性，可以直接作為計數的突破口。一烯烴的拆分如圖5所示。

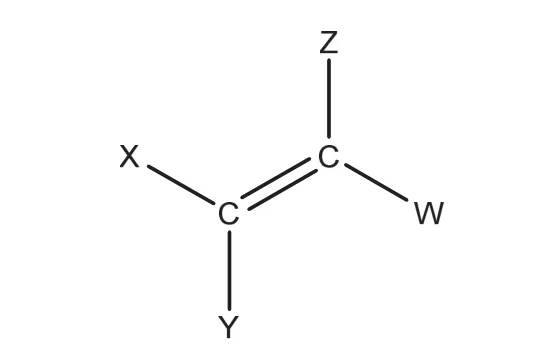
圖5 一烯烴的拆分(X，Y，Z，W為烷基)

在圖5中，不考慮順反異構，則X與Y對稱，Z與W對稱，兩側獨立且對稱。

通過前幾小節的經驗，我們可以自然推出一烯烴同分異構體計數的生成函數Calkene(x)：

其中T(x)是方程(4)中定義的烷基的計數生成函數。在實際計算時，可使用方程(5)中的遞推獲得任意范圍內的精確結果。

若額外考慮順反異構，則X, Y, Z, W之間的對稱關系可以用如下置換表示：

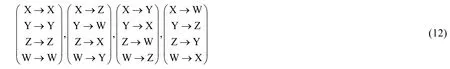
仿照節1.2中的推導，我們可以推出此時一烯烴同分異構體計數的生成函數C′alkene(x)：

快速驗證：通過手工枚舉可以得知：丁烯在不計順反異構時有3種同分異構體，考慮順反異構時有4種；戊烯在兩種情況下分別有5種和6種，這和我們的結果是相一致的。

2.4 一炔烴的同分異構體計數

一炔烴三鍵兩側的碳原子可以被視作是各連接了一個烷基，因此我們很容易地寫出一炔烴同分異構體數目的生成函數Calkyne(x)：

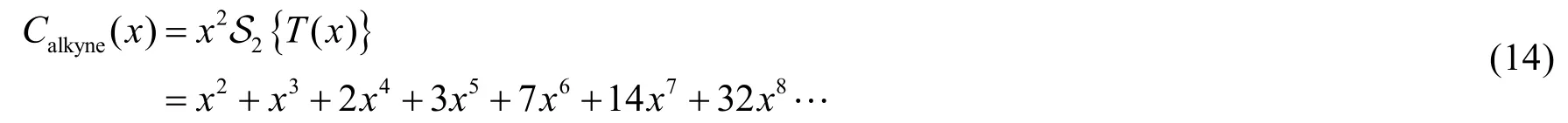
2.5 苯的衍生物的同分異構體計數

苯的衍生物可視作每一個苯環上的碳原子皆連接了一個烷基。這六個烷基的對稱關系同構于二面體群D2×6(即旋轉、翻折對稱)，因此仿照節1.2中的推導，我們可以推出對應的生成函數Cbenzene(x)：

2.6 烷烴二取代物的同分異構體計數

為了進一步說明本文方法的靈活性，我們考查烷烴二取代物的同分異構體計數。和前文單官能團的情形不同，二取代物中兩個官能團的異同會影響結構的對稱性，因此需要分類討論。

2.6.1 異官能團

仿照我們在節2.2中的思路，做出如下定義：

定義5 (二取代烷烴的主鏈)：定義連接官能團的碳鏈為二取代烷烴的主鏈，該碳鏈的長為二取代烷烴的主鏈長。

我們考查主鏈上的碳原子，并觀察到除了連接官能團和主鏈上的其他碳原子外，每個主鏈上的碳原子恰成兩鍵。兩鍵連接的子結構可以視為烷基并在結構上具有對稱性。同時，由于兩官能團不同，主鏈本身不具備對稱性。因此，對于給定的主鏈長h，我們得到對應二取代烷烴的同分異構體計數生成函數Bh(x)為：

其中x代表主鏈上的每一個碳原子， { }2T(x)S 代表該碳原子向主鏈外連接的分支。

只需要枚舉h，我們即可推出異官能團情形下烷烴二取代物的同分異構體計數生成函數B(x)：

以上假設主鏈長可以為0，對于官能團不含碳的情況(如鹵原子)，應選擇從1開始枚舉。依據官能團中碳原子的個數，對上式也可以進行一定程度的平移。

2.6.2 同官能團

同官能團的情況較異官能團更為復雜：主鏈兩端相同的官能團使得主鏈本身產生了對稱性。為避免由該對稱性導致的重數，我們需要從中心開始計數并按照主鏈長的奇偶性進行討論(這和節2.2中的處理方法是一致的)。

主鏈長為偶數：設主鏈長為2h，則主鏈長為h的兩半關于主鏈中心的碳碳鍵對稱。因此，對應二取代烷烴的同分異構體計數生成函數為：

主鏈長為奇數：設主鏈長為2h +1，則主鏈中長為h的兩半關于主鏈中心的碳原子對稱。這個需要單獨考慮的碳原子是和偶數長主鏈情況的唯一區別。因此，不難寫出的表達式：

將以上兩種情形匯總，則：

就得到了同官能團情況下二取代烷烴的同分異構體計數生成函數。

2.7 二烯烴的同分異構體計數

在完成推導二取代烷烴同分異構體計數的基礎之上，我們推導二烯烴的同分異構體計數。

我們將二烯烴的碳碳雙鍵以及連接出的三條分支視作一個“官能團”，如圖6所示：

圖6 從二烯烴到同官能團二取代烷烴的規約(X，Y，Z為烷基)

由圖6，顯然，該官能團自身同分異構體計數的生成函數可以寫為{x}2T(x)S2{T(x)}

在這個視角下，我們完成了二烯烴到同官能團二取代烷烴的規約。仿照節2.6.2的推導，二烯烴的同分異構體計數的生成函數可以寫為：

注意到由于我們規約的方式，我們在上式并沒有考慮累積二烯烴。累積二烯烴在結構上和烯烴是非常類似的，因而其計數就不多加贅述了。

至此，敏銳的讀者可以發現類似同分異構體計數的“套路”所在：識別子結構并試圖規約、考慮對稱、分部寫出生成函數、組合成為最終結果。本文希望通過以上若干例子展示生成函數結合Pólya計數定理的靈活性。

3 漸進性質探究

在上一節，我們展示了若干烴及其衍生物同分異構體計數的精確算法。在本節，我們將借用這些結果探究烴類同分異構體數目的漸進特征，即在碳原子數足夠大時，同分異構體數目的增長性質以及近似方法。這些漸進特征將有利于我們對于同分異構現象在數學上進行整體把握，也有助于估算。

需要指出的是，本節的得出的結論依賴于歸納，在嚴謹性上具有欠缺。然而嚴謹地基于生成函數分析其系數的漸進特性是解析組合學的范疇，后者的專業性使其不適宜出現在本文中，望讀者理解。

為了探究同分異構體數目隨碳原子數的增長規律，我們繪制相應的對數圖表，見圖7。

圖7 不同烴類同分異構體數目隨碳原子數的增長狀況

圖7中各烴類的同分異構體數目對應的突顯呈明顯的直線型，且斜率一致。這表明：

1) 烴類同分異構體數目的變化由指數增長的主導，與我們的直覺相符；

2) 同時，指數增長的底數不隨化合物的種類有明顯變化。看似復雜的烴類并不比簡單的烷基同分異構體數目增長快(單從指數增長的角度)，這是與我們直覺是相悖的。

為了探究共同的底數，我們對于每一種烴類同分異構體數目的數列進行鄰項作比，略去碳原子數較少時顯著的波動項，繪成圖8。

圖8 隨碳原子數增加相鄰碳原子數的同分異構體數之比的收斂狀況

從圖8我們觀察到隨著碳原子數的增加，相鄰碳原子數對應的同分異構體數目之比收斂于2.8左右，即指數增長的底數約為2.8。按照收斂的速度，圖8中的烴類又可分為三組：二取代烷烴以及二烯烴結構最為復雜，故收斂最快；烷基，一烯烴，一炔烴以及苯的衍生物次之；烷烴的結構最為簡單，因而收斂最慢。

能否在數學上刻畫這種收斂速度的差異？收斂速度的差異是由漸進式中除指數項外的因子造成的。查閱文獻可知，Flajolet和Sedgewick通過解析組合學的方法證明n-烷基同分異構體個數漸進正比于2.81546nn?3/2；n-烷烴同分異構體個數漸進正比于2.81546nn?5/2[11]。基于二人的成果，我們做出假設：

在漸進意義上，對于本文所列舉的所有烴類及衍生物，n個碳原子對應的同分異構體數目等于Cαnnk，其中α= 2.81546且C，k為常數。更激進地說，k為負半奇數。

為驗證我們的假設，對于每一種化合物，記n個碳原子的同分異構體數目為F(n)，我們繪制雙對數圖線(lnn, ln(F(n)/αn))。假說正確時，ln(F(n)/αn) =klnn+ lnC，即圖線應呈現為斜率為k，y-截距lnC的直線。

如圖9所示，所有圖線的皮爾遜相關系數都小于?0.999，展現出強線性，假說正確。

圖9 同分異構體數目除去指數項后的冪函數特征

對圖9中的每根圖線進行最小二乘擬合，得估計斜率k以及截距lnC并繪制成表1。

表1 部分烴類同分異構體計數漸進通式參數(擬合)

我們由表1觀察到所有的k都接近負半奇數，這進一步顯示了我們假設的正確性。我們將k取整到最近的負半奇數并在此之上擬合截距，得到表2。

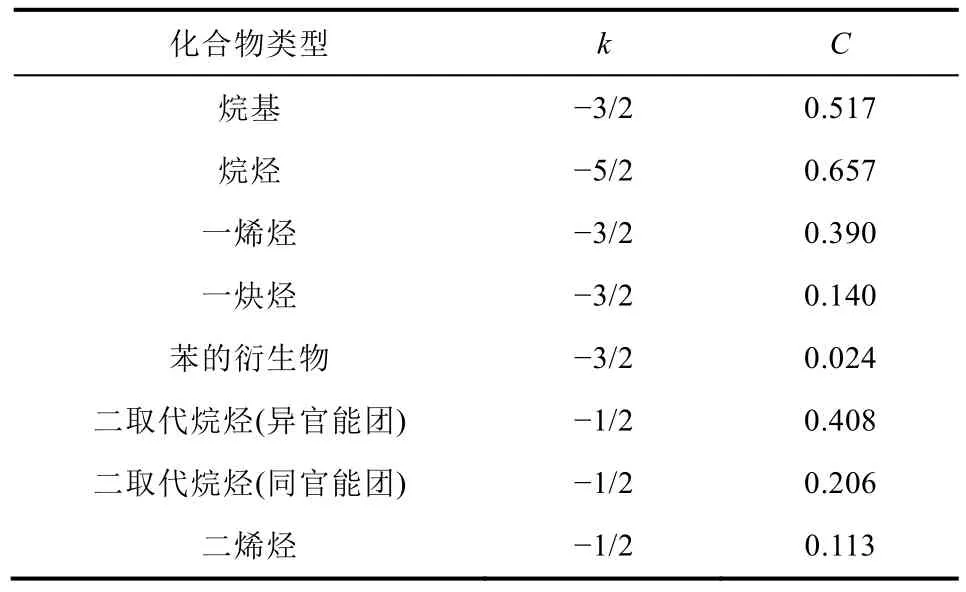
表2 部分烴類同分異構體計數漸進通式參數(修正)

按照表2中參數進行近似估算的相對誤差如圖10所示。

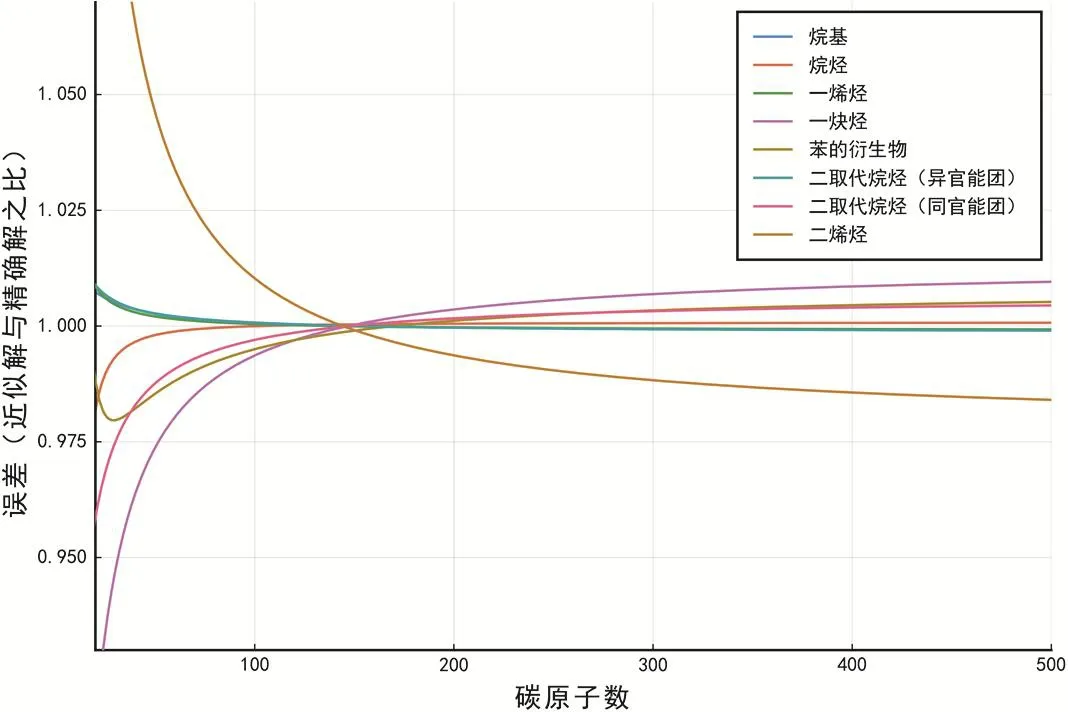
圖10 同分異構體計數漸進估算相對誤差

由圖10可知，相對誤差均呈現收斂。收斂極限與理論值1的偏差應當來源于數值計算產生的誤差與有限項擬合的局限性。為控制計算時長，本節只采用了碳原子數1至500的對應項進行擬合；我們合理地推斷：如果增加參與擬合的項數，應當能得到C的更優估計。

因此，我們的假設結合表2中參數可以得到較為優秀的近似估計。除了用于直接估算以外，我們假設的驗證成立，可以：1) 從代數角度解釋圖8鄰項比收斂的不同速率，以及更為重要地，2) 在碳原子數足夠大時，即使官能團不同，一些k相同的烴類的同分異構體個數之間存在常數比例關系。該關系使間接估算成為可能。

4 結論與展望

本文通過生成函數結合Pólya計數定理推導了烷基，烷烴，一烯烴，一炔烴，苯的衍生物，二取代烷烴以及二烯烴的同分異構體的計數公式，所得出的結果與手工枚舉的結果相符，初步印證了我們結果的正確性。我們推導的過程中展現了我們方法的簡潔性，系統性與靈活性。我們在推導的過程中同時加深了對于這些烴結構性質的理解。對于高中讀者，這也有助于在手工枚舉時更加嚴謹有序。我們隨后探究了同分異構體數目關于碳原子數的漸進特征，提出假設，并歸納性地給予一定的佐證，得到前文所述烴類同分異構體計數的簡單、優秀近似。

本文的一個主要寫作目的是向高中讀者介紹Pólya計數定理在同分異構體計數中的應用，因此拋磚引玉，所涉及到的烴類結構較為簡單，約束也較多。Pólya計數定理的能力遠不止于此。例如：單環烷烴同分異構體的計數可以通過枚舉環長，并結合二面體群的相關知識處理；含有三個乃至多個官能團的烴的同分異構體的計數可以也可以通過討論三個烷烴的位置關系進行處理；Robinson對于立體異構烷烴的計數本質上仍然是基于Pólya計數定理的[8]……鑒于上述方案需要的篇幅以及額外引入的數學背景知識，本文并未詳細展開。鑒于同樣的原因，本文關于漸進性質的假設也并未嚴謹證明。感興趣的讀者可從參考文獻出發自行探究。

補充材料：可通過鏈接http://www.dxhx.pku.edu.cn免費下載。