基于BP神經網絡的輸電線路電場屏蔽效果預測*

于利佳, 田 瑾, 吳 飛, 龔 利

(1.上海工程技術大學 電子電氣工程學院,上海201620； 2.華東師范大學 城市與區域科學學院,上海 200062)

0 引 言

如今,輸電線路產生的電磁環境對長期生活在線路周圍的居民產生了極大的影響。電磁環境影響參數主要包括工頻電場、工頻磁場、無線電干擾和可聽噪聲四個方面,其中工頻電場的影響成為公眾最為關注的問題之一。

目前,電磁場計算的方法主要有模擬電荷法[1,2]、矩量法[3]、有限元法[4]等,電磁場預測用到的模型主要有灰色預測[5]和人工神經網絡(artificial neural network，ANN)[6,7]等。作為計算超高壓輸電線路電場的主要方法,由于有限元法計算較模擬電荷準確,但此類方法通常需要建立模型后反復修改參數進行計算,可利用有限元法計算得到部分屏蔽線位置電場強度值作為訓練值。對于未知位置對應的屏蔽效果,利用反向傳播(back propagation,BP)神經網絡進行預測,因為其操作簡單、高度自學習和自適應特性,使其擁有較高預測非線性相關問題能力。

本文提出采用BP神經網絡的輸電線路電場屏蔽效果的預測模型,以500 kV同塔雙回輸電線路為例,借助有限元軟件Ansoft Maxwell搭建輸電線路模型,計算出從屏蔽線數量、架設高度以及水平位置不同角度優化屏蔽效果的電場強度值,在此基礎上,通過神經網絡將預測值與真實值進行對比驗證模型的可行性和準確性,結果可為超高壓輸電線路電場環境優化及建設提供參考依據。

1 神經網絡模型

1.1 人工神經網絡

人工神經網絡是由大量神經元廣泛相互聯結而成的非線性的、動態的復雜網絡信息處理系統。起源于現代神經學研究成果,能夠模擬人腦的基本功能。它能夠從累積的案例中學習知識,將各種定量或定性的因素盡可能地作為變量加以輸出,建立因素與結論間的非線性映射,采用自適應模式識別的方法來完成預測工作[8]。

神經元模型如圖1所示。

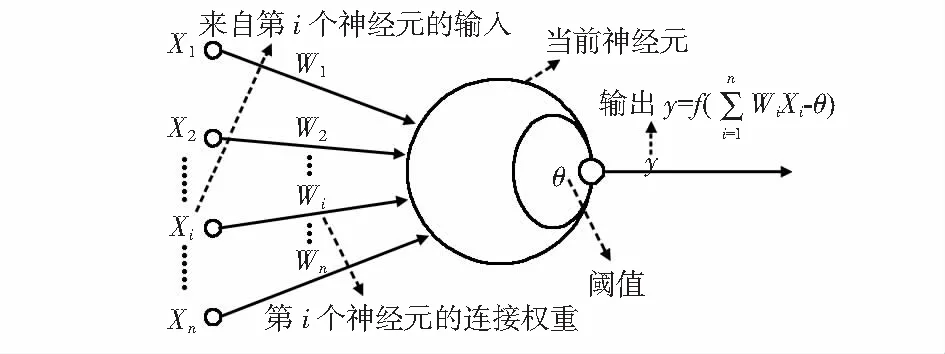
圖1 神經元模型

圖1中顯示,n個神經元通過連接權重將信息整合到神經元匯總,然后和閾值作比較,最終通過相關激活函數輸出預測值。常用的激活函數有Sigmoid函數

Sigmoid=1/(1+e-x)

(1)

1.2 BP神經網絡

在人工神經網絡中,前饋BP神經網絡使用的最多。通常BP神經網絡由三層結構組成,如圖2所示。

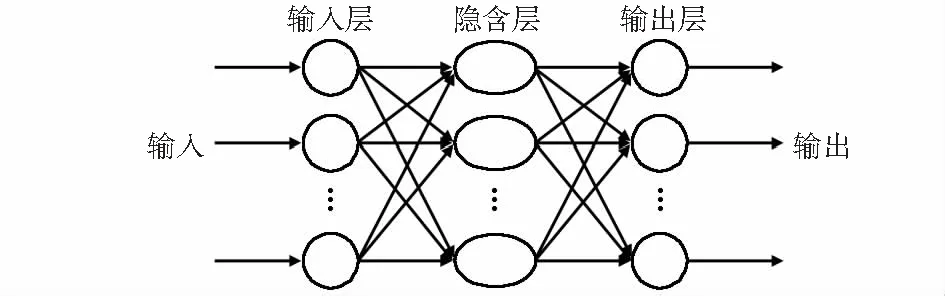
圖2 多層前饋神經網絡結構

左右各層神經元由連接權值連接,上下并無連接。BP神經網絡是有導師神經網絡,在初期會給一個學習模式,最終神經元學習該模式進行傳播,輸出預測結果。隱含層單元誤差和下降梯度是否需要計算且通過修改權重與閾值來重新學習,主要取決于實際輸出和期望輸出之間的誤差是否滿足精度要求,通過迭代操作可使輸出值結果更加準確[9]。具體BP神經網絡學習算法流程如圖3所示。

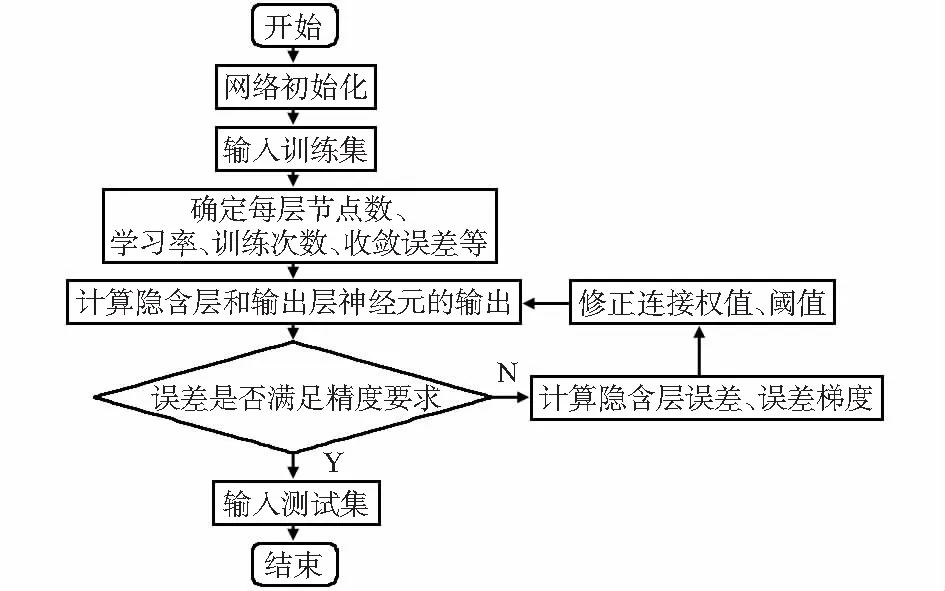
圖3 BP神經網絡模型算法流程

2 輸電線路屏蔽模型

國內外針對輸電線路電磁場研究表明[10],工頻電場強度除了隨導線架設位置、結構等參數變化外,還可以通過架設屏蔽線降低工頻電場強度。因此,為研究線下工頻電場屏蔽效果,本文以500 kV同塔雙回輸電線路為對象分析架設屏蔽線對線下1.5 m處電場的影響,其中屏蔽線型號為LGJ—240/30,如圖4所示,h為屏蔽線的對地高度,d為兩側屏蔽線到線路中心的水平距離。通過改變三根屏蔽線的位置,可以得到相應的工頻電場強度值。

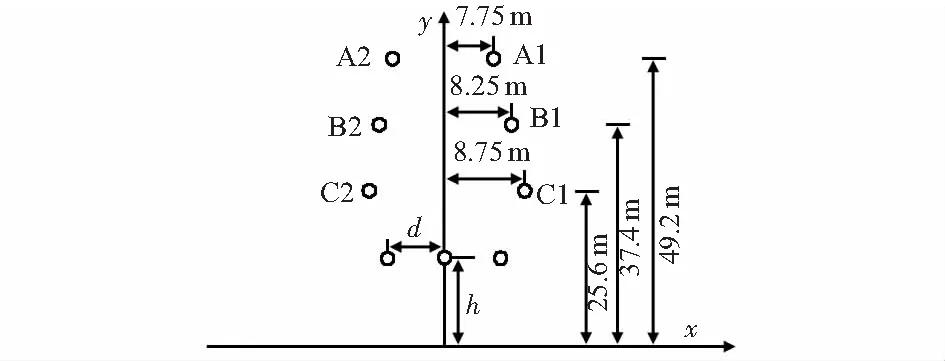
圖4 架設屏蔽線計算模型

3 基于BP神經網絡的電場強度預測模型

3.1 電場強度預測模型的構建

實際生活中,針對未建好的輸電線路,通常需要提前進行預測,而針對已建好的輸電線路,通常處于山區或鬧市區,不易測量或成本過高[11]。因此,本文提出建立合理準確的電場強度屏蔽線優化預測模型。

由文獻[12,13]可知,輸電線路線下電場強度與屏蔽線架設高度和水平位置均有關,但這種關系是非線性的,不易通過數學公式直接計算得到。因此,本文將部分已知的輸電線路屏蔽線對地高度、水平位置和相對應的電場強度數據作為訓練集,將其他已知的屏蔽線對地高度、水平位置作為測試集數據,通過將預測結果和電場強度真實值進行對比建立BP神經網絡模型進行驗證。

基于BP神經網絡電場強度預測模型具體步驟如下：

1)建立訓練集：本文對500 kV同塔雙回輸電線路屏蔽線數據進行整理,取屏蔽線參數不同的44組數據(包括：屏蔽線對地高度、水平距離和相對應的電場強度)作為訓練集輸入。

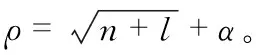
3)建立測試集：將500 kV同塔雙回輸電線路屏蔽線數據進行整理,取屏蔽線參數不同的12組數據(包括：屏蔽線對地高度、水平距離和相對應的電場強度)作為測試集輸入。

3.2 電場強度預測結果分析

通過改變500 kV同塔雙回輸電線路架設屏蔽線對地高度、水平距離,得到44組不同數據工頻電場強度值。

通過MATLAB對表中數據采用BP神經網絡訓練,仿真過程如圖5所示。

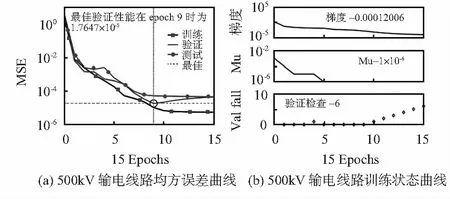
圖5 500 kV輸電線路均方誤差與訓練狀態曲線

神經網絡在訓練數據中,會將數據按照一定比例分為訓練集(training set)、驗證集(validation set)和測試集(testing set),以便模型的預測準確性。其中訓練集主要是對數據樣本進行模擬擬合,驗證集負責尋找最優的網絡深度,測試集負責最終模型的泛化能力,即預測準確性。

本文訓練算法選取的是萊文貝格—馬夸特法(Levenberg-Marquardt algorithm),該算法可結合高斯—牛頓算法以及梯度下降法的優點,并對不足之處進行改善。如圖6所示,Train,Validation和Test曲線分別表示訓練樣本、驗證樣本和測試樣本。模型迭代次數為9時,驗證樣本的均方誤差(mean squared error,MSE),即均方誤差最低為0.000 017 6,性能最好,經過更多訓練階段后,隨著網絡過度擬合訓練數據,驗證誤差連續迭代6代不減反增,因此模型在第15次迭代后結束。 經過分析可知,該模型訓練樣本相關系數R=0.999 94,驗證樣本相關系數R=0.999 92,測試樣本相關系數為R=0.999 51,樣本總的相關系數為R=0.999 88,整體模型訓練效果較好。

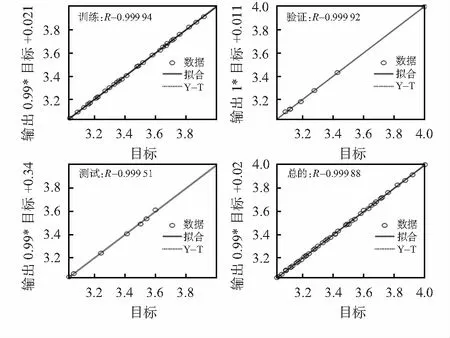
圖6 500 kV輸電線路回歸

本文將12組500 kV同塔雙回輸電線路架設屏蔽線對地高度、水平距離數據作為預測模型的輸入集建立神經網絡預測模型,并將預測結果和真實值進行對比。

將工頻電場真實值和模型預測值作出對比圖,如圖7所示,基于BP神經網絡建立得訓練模型對輸電線路屏蔽效果進行預測,預測值與真實值最大誤差為0.6 %,具有較好的預測效果。

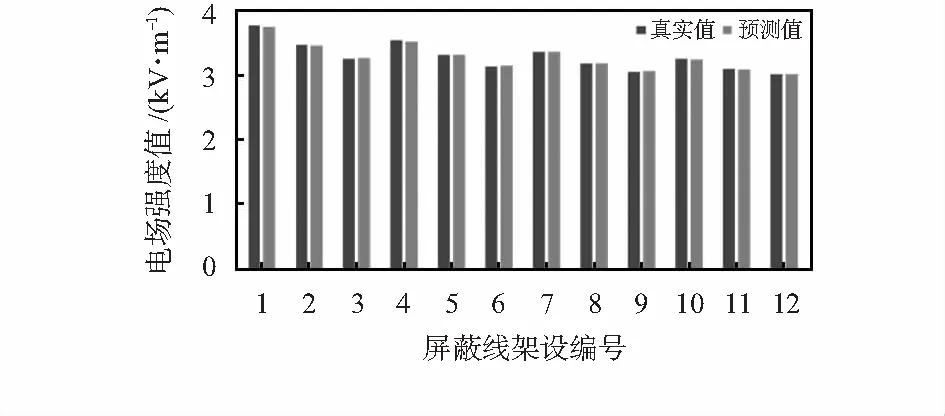
圖7 500 kV輸電線路電場強度對比

4 結 論

本文首先建立輸電線路屏蔽線模型,從屏蔽線數量、架設高度以及水平位置不同角度研究優化屏蔽效果,得到部分不同位置下電場強度值,并利用BP神經網絡預測未知位置下電場強度值,經對比結果表明,預測值與真實值誤差很小,具有較好的預測效果。