基于PVDF的仿生側線傳感器設計與標定

丁 峰, 肖如慧, 魏新民, 王淑杰, 孫文彩, 談世哲

(中國海洋大學 信息科學與工程學院 電子工程系,山東 青島 266100)

0 引 言

傳統的海流測量方法包括機械旋漿式、電磁式、聲學式和光學式[1]。這些方法既有各自的優點,也存在著一定的不足。機械式海流計的工作深度受限較小且功耗低,但對低速測量存在較大誤差；電磁式海流計體積小使用靈活,但易受海水介質導電率和地球磁場影響；聲學式海流計會受到海水溫度、鹽度、懸浮顆粒、聲學散射以及多徑傳播的影響,造成測量精度下降；光學式海流計精度會受到海水渾濁度的影響,導致測量失效。因此,新型海流測量傳感器的設計與研制具有重要意義。

研究發現,魚類的側線系統可感知水流,為新型海流測量傳感器的設計提供了新思路。Chen N的團隊提出了另一種高靈敏度的壓阻式流速傳感器,使用SU—8環氧樹脂制造高長寬比的感知纖毛,其在振蕩流下的測量閾值為0.7 mm/s[2]。佐治亞理工學院的Peleshanko S等人,采用精密滴落涂布法制造出水凝膠包覆的仿生纖毛感知系統,測量閾值達到了2.5 μm/s[3]。中國海洋大學的Yang Y等人設計了一種微壓力傳感器組成的仿生側線傳感器陣列實現湍流速度估計及障礙物躲避[4]。Abdulsadda A T和Tan X提出了基于IPMC的仿生側線傳感器原型[5]。

然而上述研究在仿生側線傳感器的設計方面,材料的運用仍處于探索階段,其結構設計還只是對魚類神經丘結構的簡單模仿,缺乏對傳感器結構參數的優化；傳感器的理論模型也只是處于理論論證階段。因此,可運用于工程的仿生側線傳感器較少、傳感器結構參數優化方法相對匱乏、傳感器對應模型理論體系不夠完備是當前研究所面臨的主要問題。

針對上述仿生側線傳感器研究目前所面臨的主要問題,本文參考魚類體表神經丘的形態結構與傳感機理,采用壓電特性突出的聚偏二氟乙烯(polyvinylidene fluoride,PVDF)壓電薄膜作為感知單元設計仿生側線傳感器,采用計算流體動力學(computational fluid dynamics,CFD)技術優化傳感器結構參數,并通過理論分析建立傳感器的理論模型,通過水箱標定實驗完成傳感器的標定、精度分析,制作出可運用于工程的仿生側線傳感器。

1 魚類側線感知機理

魚類體表神經丘位于魚類的表皮上,是由纖毛細胞及其感知纖毛束組成的小型受體器官。單個纖毛細胞中有多個纖毛束,纖毛束由一根動纖毛和幾根較短且長短不一的靜纖毛組成[6],單個神經丘中所有纖毛細胞的纖毛束都處在一個大的透明殼斗中,其形態結構如圖1所示。

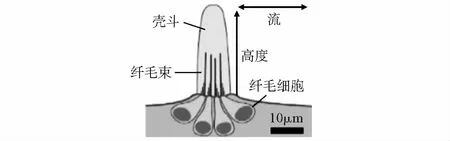
圖1 魚類體表神經丘的形態結構

體表神經丘的傳感原理在于其末端的靜纖毛偏轉會通過離子通道引起刺激或抑制反應。當魚類體表周圍的水發生流動時,體表神經丘的殼斗狀結構會傳遞水動力,該力使感知纖毛束發生傾斜,引起其下方的神經元產生神經沖動[7]。神經沖動由神經末梢傳遞給神經中樞,從而感知水流的強度和方向。

2 傳感器設計與制作

2.1 傳感器設計

根據魚類體表神經丘的形態結構和傳感原理,仿生側線傳感器的結構設計如圖2 所示。傳感器主要由探頭、懸臂梁和感知單元三個部分組成。

圖2 仿生側線傳感器設計

探頭部分參考神經丘殼斗的形態結構,被設計為殼斗形狀。探頭與外界水環境直接接觸,用以感知水動力,然后將該力傳遞給懸臂梁。懸臂梁部分則參考丘腦運動會引起纖毛束偏移的特性,被設計為長圓柱體。懸臂梁在受到探頭傳遞的力后發生偏轉,并通過杠桿結構將力進一步傳遞至感知單元。感知單元與魚類纖毛束下方的神經元作用類似,受到懸臂梁傳遞來的力之后發生形變,并進行水流信息的最終感知。

考慮到整個傳感器的尺寸、傳感器載體的局限性以及對流場的影響,仿生側線傳感器的最終結構參數如表1所示。其優化過程將在第3章中詳細介紹。

表1 仿生側線傳感器結構參數 mm

2.2 傳感器制作

考慮到傳感器的工作環境,探頭和懸臂梁的材料應具有較強的耐腐蝕性和耐水性。目前,3D打印技術[8]已非常成熟,所用樹脂材料具有重量輕、耐水性好等特點,很好地滿足了上述材料的要求。因此本文采用3D打印技術,使用樹脂材料制作探頭和懸臂梁。

目前,常見的壓電材料有PVDF、壓電陶瓷、鈦酸鋇等。而PVDF具有一些明顯的優勢：其電壓常數比壓電換能器(piezo-electric transducer,PZT)高一個量級,是聚合物壓電材料中壓電性能最好的[9]；頻率響應范圍大；生物兼容性好[10，11]。考慮到仿生側線傳感器對微小水流的感知能力,本文選擇PVDF壓電薄膜作為感知單元材料。

將質量塊固定在PVDF壓電薄膜前端,一方面可以改變傳感器的諧振頻率和靈敏度,以適應不同的應用場合；另一方面可以更好地組裝PVDF壓電薄膜與懸臂梁。電極位于壓電薄膜尾端,通過導線與放大電路相連。組裝后的傳感器如圖3(a)所示,隨后對傳感器進行硫化水密處理,其實物圖如圖3(b)所示。

圖3 仿生側線傳感器實物

3 結構參數優化

3.1 探頭結構參數優化

本文設計了翼型、拋物線形、半橢圓形、半圓形四種形狀探頭。使用Fluent模塊對四種探頭進行仿真分析,比較不同探頭在相同流速沖擊下的表面壓力分布和速度場,選出性能最優的探頭形狀。

建立四種形狀探頭模型,探頭底部寬度為6 mm,翼型、拋物線和半橢圓高度為5 mm,流體流速為0.3 m/s。將流體仿真后的探頭表面靜壓分布數據提取并整合,結果如圖4所示。從圖4中可以看出四種形狀探頭沿軸向的靜壓分布,拋物線形和翼型探頭表面的靜壓分布下降趨勢稍緩,說明流體經過拋物線形和翼型時的附著性能更好,可以更好地感知流體作用力。再對這兩種形狀探頭的速度場進行分析。如圖5所示,翼型探頭上、下方流場的流速變化明顯小于拋物線形,說明翼型對流場的擾動更小,測量值會更加接近真實值。因此翼型探頭具有最優的水動力特性。

圖4 四種形狀探頭沿軸向的靜壓分布

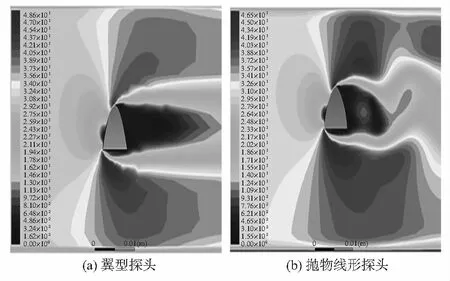
圖5 探頭速度場分布

3.2 懸臂梁和感知單元結構參數優化

本文對40,50,60,70 mm 4種長度的懸臂梁進行了流體仿真和壓電分析。首先,使用Fluent軟件計算不同流速下流體對感知單元自由端的作用力；然后，根據PVDF壓電薄膜的參數,采用機械APDL軟件對傳感器進行壓電分析；最后，得到不同懸臂梁長度下傳感器輸出電壓與流速的關系圖。由圖6可知,當流速固定時,傳感器輸出電壓隨懸臂梁長度的增加而增大。

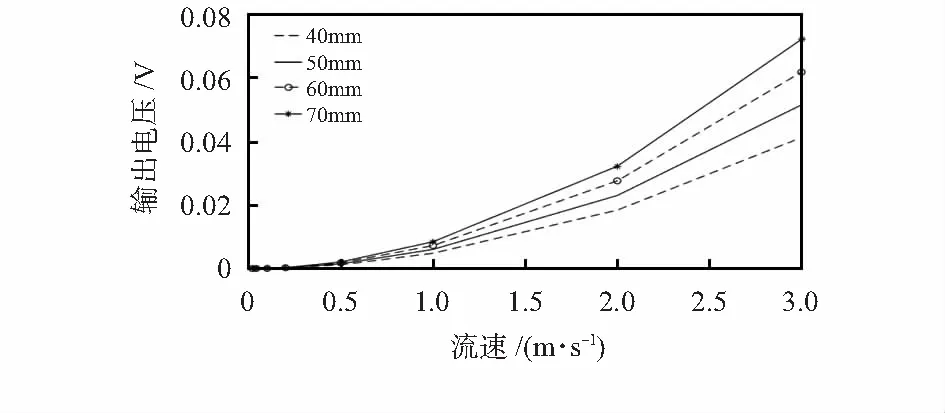
圖6 不同懸臂梁長度的傳感器速度—電壓關系

為了選擇最合適的懸臂梁長度,有必要參考測量系統的總噪聲。本文所使用的測量系統總噪聲約為6mV,因此，傳感器的最小輸出電壓不能低于6 mV。結合圖6,同時考慮一定的余量,傳感器最小感知流速被設定為1.5 cm/s,因此，懸臂梁的長度至少應為60 mm。此外,考慮到傳感器對外部流場的干擾應盡可能減小,故應選擇較短的懸臂梁。因此,懸臂梁的長度最終設定為60 mm。

采用相同的分析方法對PVDF仿生側線傳感器的其他結構參數進行優化,可得到它們的最優參數值：懸臂梁的直徑、感知單元的長、寬、厚度分別為2,25,11,0.1 mm。

4 理論建模

流體對探頭迎流面的壓力效應非常復雜,在分析探頭受力與流體間的關系時,需要考慮多種流動條件。但如果流動條件簡單且定義明確,則可通過受力分析得出兩者之間的關系。根據流體力學基本理論,PVDF仿生側線傳感器探頭所受壓力可表示為

(1)

式中Cd為粘性系數；A為探頭迎流面面積；ρ為流體密度；v為流體速度。

懸臂梁采用杠桿結構,可以放大作用在探頭上的力,根據杠桿原理

FD=Pd

(2)

式中P為傳感器探頭所受壓力；d為傳感器的總長度；D為PVDF壓電薄膜的長度；F為作用于PVDF壓電薄膜自由端的力。

PVDF壓電薄膜形狀為長條形,一端固定,另一端可自由彎曲,其可簡化為自由端集中荷載的懸臂梁結構。根據懸臂梁基本理論,其應力T1可表示為

(3)

式中M為力矩；w和h別為PDVF壓電薄膜寬度、厚度。

因此懸臂梁的力矩公式可表示為

M(x)=F(l-x)

(4)

式中F為PVDF壓電薄膜自由端受力；l為PVDF壓電薄膜的長度。

則PVDF壓電薄膜的表面電荷量可以表示為

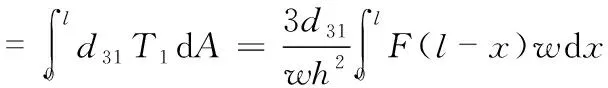
(5)

式中d31為X軸方向上的壓電常數。

PVDF壓電薄膜輸出的電荷信號一般為PC級,因此,采用電荷放大電路作為傳感器的一級放大電路。為了靈活地調節電荷放大電路轉換后的電壓信號幅值,二級放大電路為負反饋網絡電壓放大電路。因此,傳感器輸出電荷信號Q與放大電路輸出電壓Uout之間的關系可以表示為

(6)

式中Cf為放大電路的電容；K為放大電路的放大系數。

結合以上分析,傳感器理論模型可表示為

(7)

5 水箱實驗

5.1 標定實驗

首先,將PVDF仿生側線傳感器與多普勒流速儀固定在一起,保證其速度的一致性,并將流速儀固定在水箱實驗平臺的導軌上,帶動其移動。然后,通過放大電路對傳感器輸出信號進行放大,并由數據采集器采集至個人電腦(PC)。最后,將流速儀測得的流速作為實際流速導入PC機,結合傳感器理論模型,進行數據曲線擬合。水箱實驗平臺如圖7所示。

圖7 水箱實驗平臺

步進電機的速度區間為0.02～0.50 m/s,間隔為0.04 m/s。每個速度重復采樣5次,以流速儀測得的平均值作為實際流速,以傳感器輸出電壓平均值作為相應流速下的實際輸出電壓。根據傳感器理論模型,輸出電壓與流速的平方成正比,因此,對數據進行二次曲線擬合,結果如圖8所示。擬合后的和方差為0.000 252 3,決定系數為0.994 2,擬合效果良好。因此,PVDF仿生側線傳感器的輸入輸出關系可校準為

Uout=0.552 4 ×v2

(8)

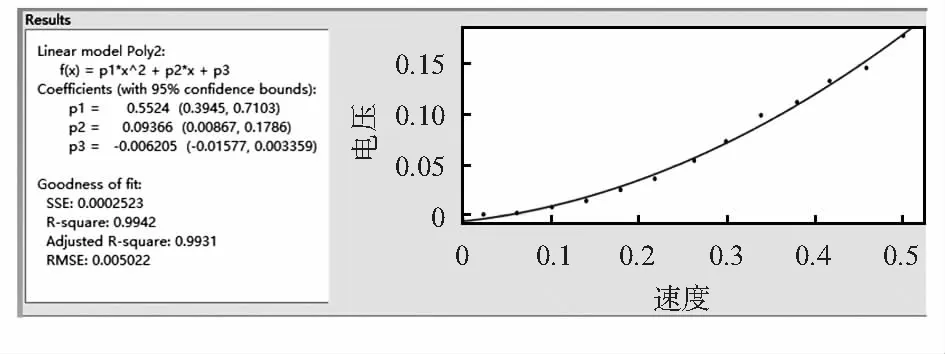
圖8 曲線擬合結果

5.2 精度分析

傳感器精度可以用測量范圍內最大基本誤差的絕對值與傳感器滿標度輸出之比的百分比表示。再次進行水箱標定實驗,將傳感器輸出電壓代入標定后的傳感器輸入輸出關系,得到PVDF仿生側線傳感器測量的流速,進而計算基本誤差。計算結果見表2。

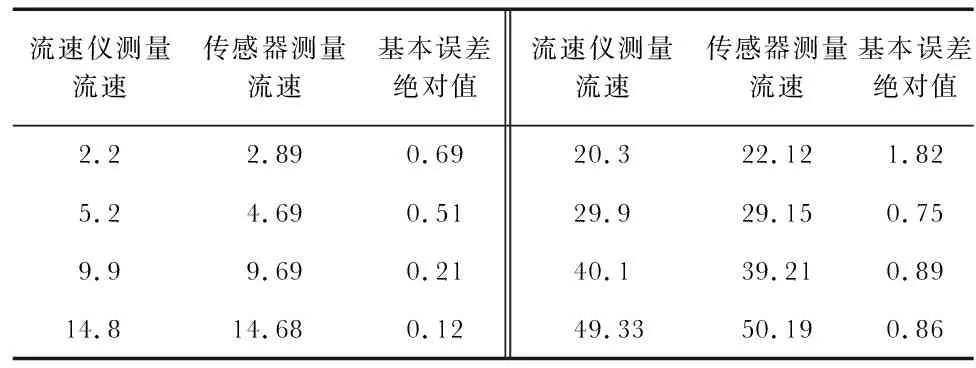
表2 水箱實驗基本誤差 cm·s-1

由表2可知,基本誤差最大值為1.82 cm/s,由于水箱長度和電機控制調速的限制,本次水箱標定的流速范圍為0.02～0.5 m/s。以PVDF仿生側線傳感器的全量程為50 cm/s,可計算出PVDF仿生側線傳感器的精度為3.64 %。

6 結 論

本文根據魚類體表神經丘的形態結構和傳感機理,設計了傳感器結構；利用Ansys仿真軟件對傳感器各部分的結構參數進行優化；通過理論分析,建立了傳感器理論模型,并通過實驗對傳感器的輸入輸出關系和精度進行了標定。結果表明：本文研制的PVDF仿生側線傳感器實際測量值與理論模型擬合良好,流速測量范圍為0.02～0.5 m/s,流速測量的精度小于4 %。能較好地進行了水下流速的測量。