基于5次NURBS的六足機器人足端軌跡規劃

周敬東，汪 宇，高偉周，楊 磊

(湖北工業大學湖北省農業機械工程研究設計院，湖北 武漢 430068)

軌跡規劃是六足機器人實現行走功能的重要環節。軌跡規劃方法有兩種：一是在操作空間內，機器人足端行走過的路徑比較直觀，容易觀察，但是該方法未考慮運動的奇異性，運動需要經常計算逆解；二是在關節空間中，通過運動學逆解方程，將笛卡爾空間中腿部所處的位置時間序列與其關節空間中的位置時間序列相對應，該方法對關節的角速度和角加速度有一定程度上的約束，還避免了運動奇異性[1]。

在實際研究中，軌跡規劃有多種方法，例如梯形法、正弦法[2]、多項式以及B樣條[3-4]等。其中，NURBS(非均勻有理B樣條)曲線插值法能保證軌跡規劃時角度、角速度和角加速度不發生突變且穩定性良好，軌跡曲線在控制頂點形成的凸狀包之內，便于軌跡的控制與關節的約束[5]。

綜上所述，已知六足機器人腿部足端首末兩端位置，通過機器人逆運動學得到腿部各關節的角度和角速度，再基于5次NURBS曲線插值法進行擬合，得到各關節的角度、角速度以及角加速度曲線，從而實現對六足機器人的足端軌跡規劃[6-7]。

1 機器人腿部位姿描述

1.1 機器人腿部正運動學分析

機器人腿部由基節、股節和脛節三部分組成，機器人機體和這三部分肢節分別通過基關節、股關節和脛關節進行連接[8]。對機器人腿部進行正運動學分析，即根據機器人機體的位置和三個關節的角度，計算出腿部足端末點的位置坐標的過程[9]。使用D-H方法在機器人的某條腿上建立坐標系(圖1)。機器人腿部的D-H的相關參數如表1所示。

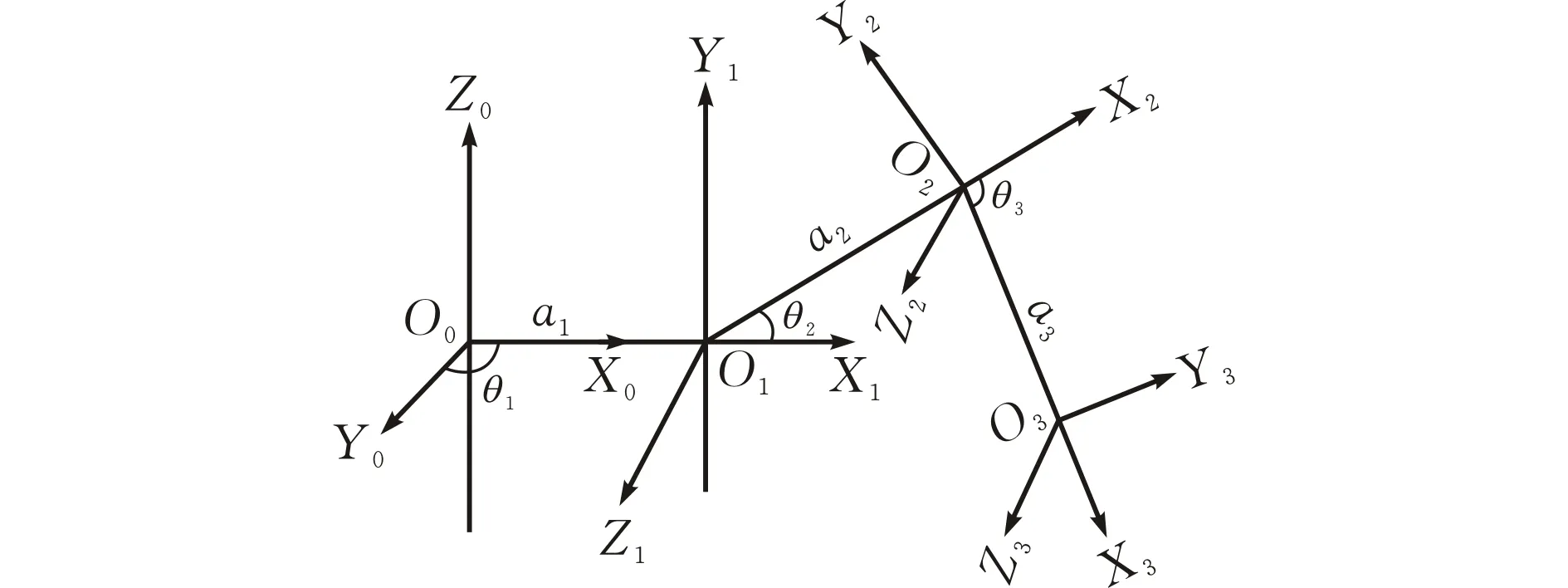
圖 1 機器人腿部坐標系

表1 D-H參數

通過代入D-H參數，機器人腿部各關節之間的變換矩

(1)

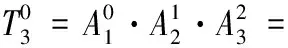
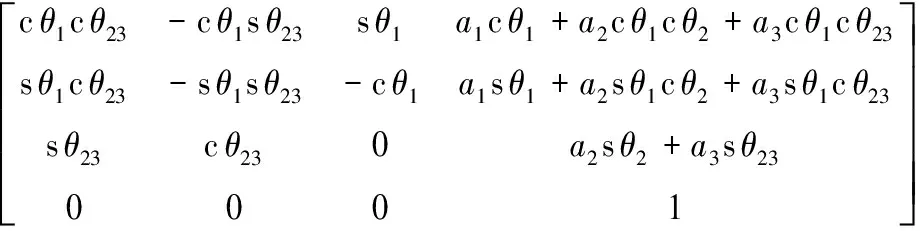
(2)

式中：cθ1=cosθ1，sθ1=sinθ1，sθ23=sin(θ2+θ3)，cθ23=cos(θ2+θ3)。

機器人腿部足端點各坐標為：

(3)

1.2 機器人腿部逆運動學分析

對機器人腿部進行逆運動學分析，根據機器人某條腿足端末點的位置，利用左乘逆變換矩陣，計算出這條腿上各個關節角度的大小：

(4)

(5)

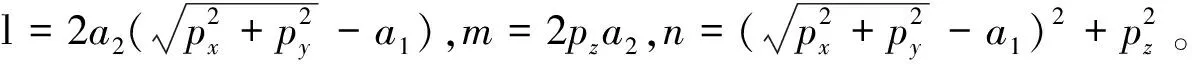
六足機器人的腿部雅克比矩陣和各關節角度的關系為：

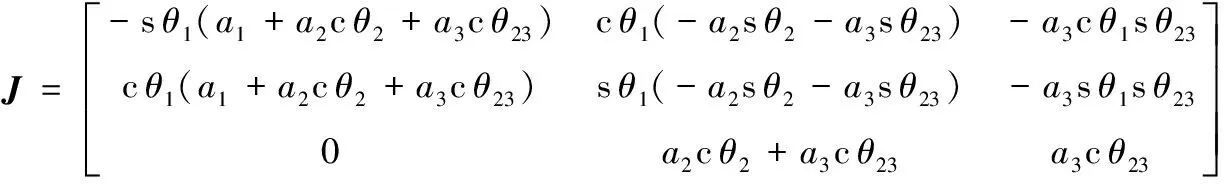
(6)

在求出機器人腿部的雅克比矩陣后，可以通過足端點的線速度來得到腿部各關節的角速度，兩者之間的關系為：

(7)

式中，vx，vy，vz分別為腿部足端點在x軸、y軸、z軸的線速度。

2 基于5次NURBS的軌跡規劃

六足機器人的足端軌跡規劃包含的內容有：根據機器人的運動過程與軌跡，確定相應的軌跡參數，利用MATLAB軟件進行模擬和描述；進行相應的計算，求解出機器人足端對應的各關節的角度、角速度和角加速度[10]。本文研究的六足機器人選擇在笛卡爾空間中進行軌跡規劃，通過機器人逆運動學求解關節空間中的各關節角度，再結合5次NURBS曲線插值法得到關節運動軌跡曲線。

NURBS又稱為非均勻有理B樣條，它能對曲線進行精確的解析，可快速穩定地計算出相應的結果，所以本文將NURBS曲線設置成機器人腿部關節空間軌跡曲線的插補方法。NURBS曲線可以設置起終點的角速度和角加速度,除此之外，還能進行特定點的優化配置，使其保持連續。表達式為[11]：

(8)

式中：di(i=0,1,...,n)是對應曲線的控制頂點；Ni,k(u)(i=1,2,…,n)是k次規范B樣條基函數，基函數可定義為：

(9)

式中：k為NURBS的次數；i為NURBS的序號。u=[u0,u1,…,un+2k]，是k次NURBS軌跡曲線定義域的節點矢量。須對時間節點進行歸一化處理：

(10)

式中，Δti=ti+1-ti。將[uk,un+k]區域內的節點應用于插值的n+1個數據點pi的k次B樣條曲線方程，得到符合插值條件的相應方程[11]：

(11)

k次B樣條需要增加k-1個邊界條件。設兩端節點重復度為k，B樣條曲線的首端和末端的控制點等同于首端和末端的數據點，相應的邊界條件為：

(12)

對式(12)的n+k個方程進行聯立，就可以解出控制頂點di(i=0,1,…,n)[11],再利用前面的公式進行推演，就可以解出k次B樣條基函Ni,k(u)(i=1,2,…,n)，進而解出機器人腿部運動軌跡上每一個點對應的關節位置p(u)，再對得到的NURBS曲線進行求導，最終求解出機器人腿部各關節在運動過程中的角速度和角加速度。

3 仿真及分析

本文所研究的機器人腿部基節、股節和脛節的長度分別為a1=50 mm，a2=70 mm，a3=140 mm。對機器人腿部在關節空間中以點到點的方式來控制軌跡，所經過的機器人腿部足端位置坐標依次為(0，130，-30)、(4，140，-15)、(8，150，10)、(12，160，20)、(16，170，10)、(20，180，-15)、(24，190，-30)。代入六足機器人的運動學模型進行逆解，得到各關節在不同位置時的角度θ1、θ2、θ3。

將整個運動行程機器人腿部足端初始端點、末端點以及求解出來的相應位置的各關節角度通過5次NURBS曲線插值法進行軌跡規劃，規定機器人腿部運動的時間為2 s，各關節初始和終止角速度為0。通過MATLAB對機器人腿部進行足端軌跡規劃仿真，得到機器人腿部足端在關節空間里的運動軌跡曲線(圖2)。腿部各關節的角度、角速度和角加速度隨足端在關節空間里位置的變化而發生改變。圖3—5為各關節在關節空間內的角度、角速度和角加速度變化曲線[12]。

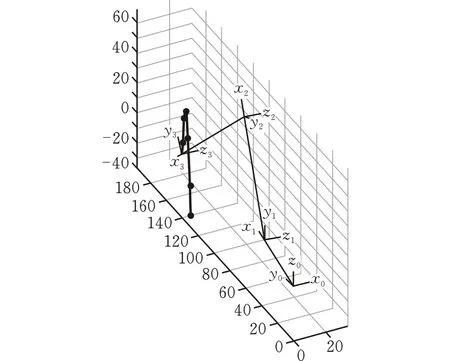
圖 2 腿部足端關節空間軌跡

從圖2可以看出，機器人足端經過的點的位置與規劃的點的位置一致，且軌跡曲線光滑連續，表明5次NURBS曲線插值法能成功應用于足端軌跡規劃。由圖3—5可知，機器人腿部各關節角度、角速度以及角加速度的軌跡曲線平滑而且連續，在加減速過程中沒有產生突變的情況，能使機器人足端穩定著陸，減少了角度變化對腿部產生的沖擊，從而有利于實現機器人腿部的平穩以及快速運動。

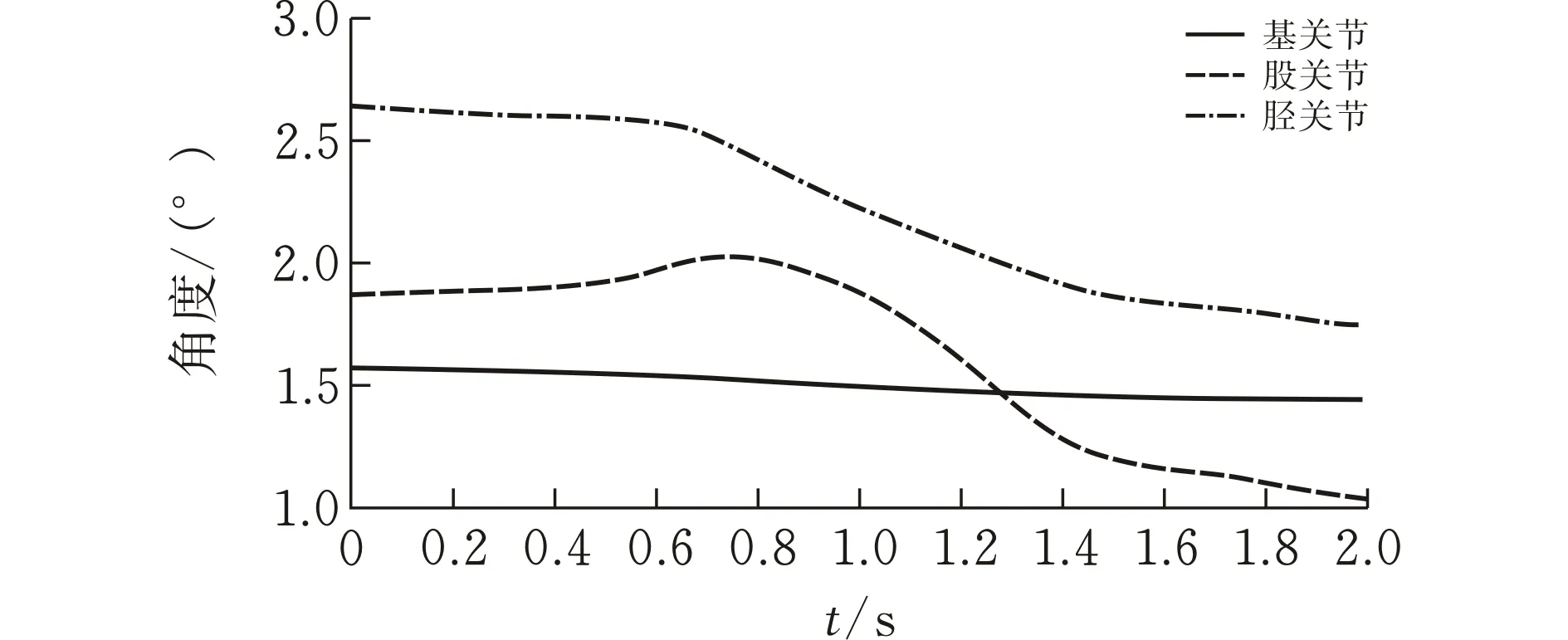
圖 3 腿部各關節角度軌跡

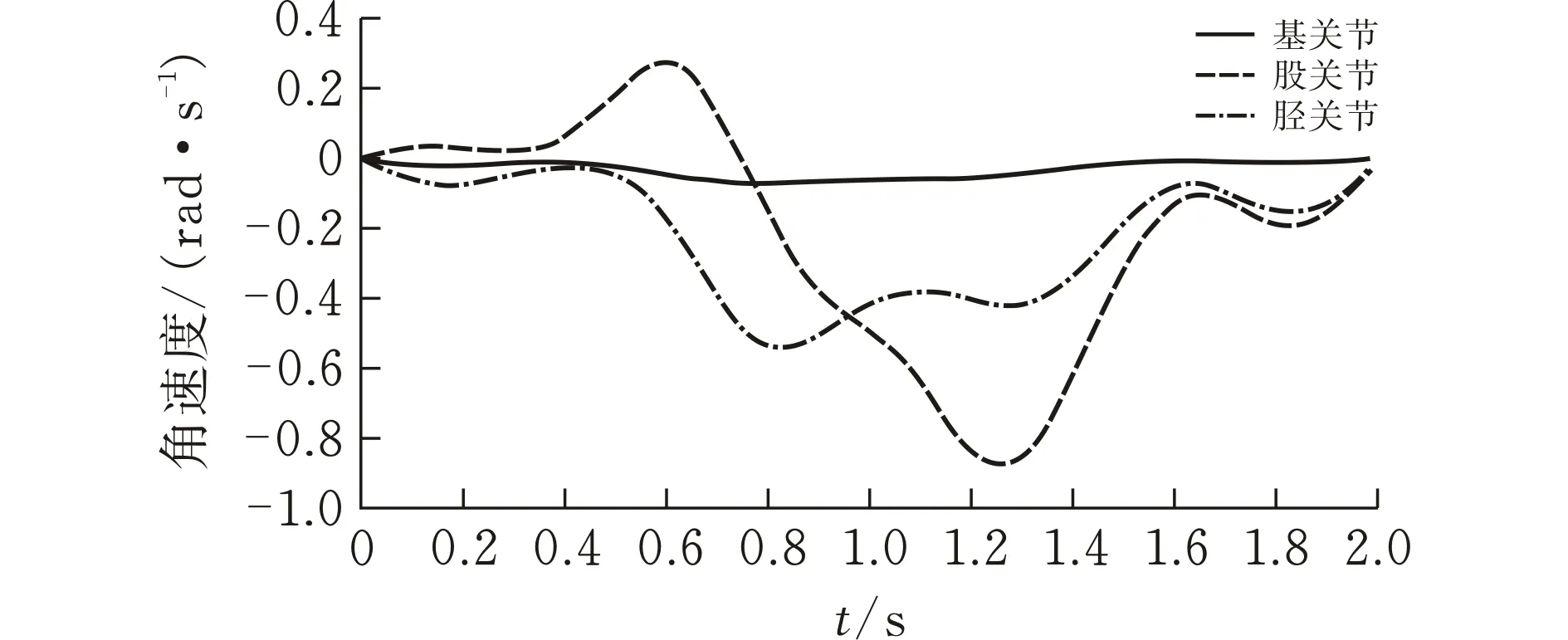
圖 4 腿部各關節角速度軌跡

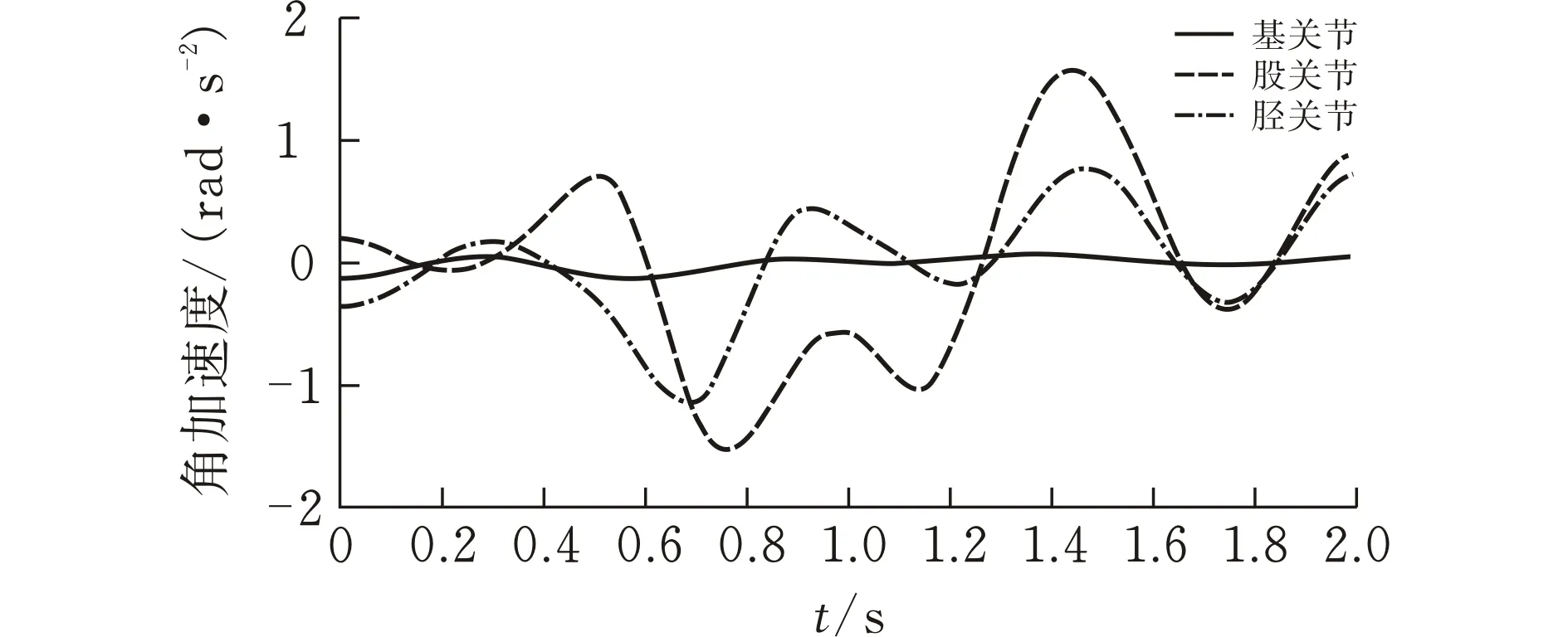
圖 5 腿部各關節角加速度軌跡

4 試驗

針對基于5次NURBS插值法的軌跡規劃，以六足機器人為研究對象，機器人和試驗環境如圖6所示。設置機器人腿部足端起點為(0，130，-30)，終點為(24，190，-30)，運行時間為2 s.在腿部運動過程中，將規劃形成的腿部足端位置信息和時間點輸入到機器人控制系統當中，通過上位機導入相應程序代碼以控制機器人腿部足端進行軌跡規劃，得到機器人腿部在x、y、z方向上的位移曲線。圖6為未引入5次NURBS插值法的機器人足端坐標軸方向位移曲線圖，圖7為引入5次NURBS插值法后的機器人足端坐標軸方向位移曲線圖。

圖 6 六足機器人

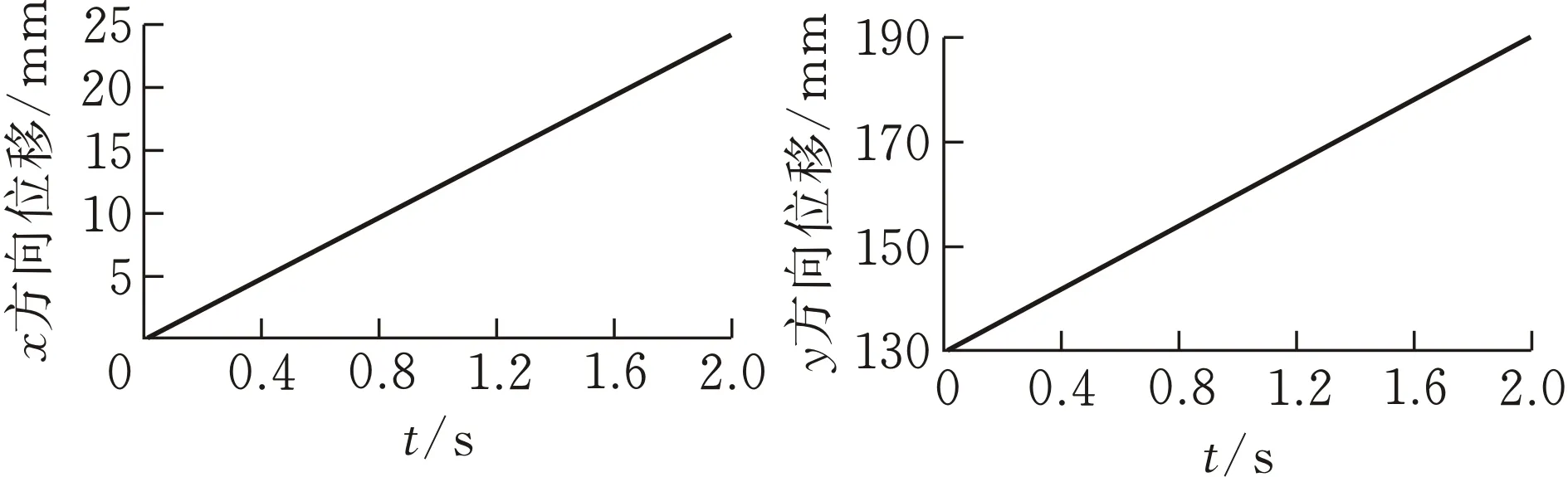
(a)x方向位移 (b)y方向位移

(a)x方向位移 (b)y方向位移

試驗結果表明：未引入5次NURBS插值法時機器人腿部運動加減速過程不明顯，易產生沖擊；引入5次NURBS插值法后，機器人腿部足端在實際運動過程中運動軌跡光滑連續，加速和減速過程明顯，使得機器人腿部運動更加平穩，試驗結果與仿真結果一致，證明采用5次NURBS插值法進行軌跡規劃的可行性。

5 結論

在對六足機器人運動軌跡優化的過程中，為提高機器人腿部運動的穩定性和準確性，本文基于機器人正逆運動學，采用5次NURBS曲線插值法對六足機器人的足端軌跡進行規劃。根據機器人腿部足端所處的位置，通過機器人正逆運動學計算，得出機器人抬腿過程中所經過位置的各關節角度以及角速度，再用5次NURBS曲線插值法進行仿真擬合，得到腿部各關節角度、角速度和角加速度變化，再通過試驗得到機器人腿部在x、y、z方向上的位移曲線。仿真和試驗結果表明：基于5次NURBS的足端軌跡規劃的關節角度、角速度和角加速度的軌跡較為光滑，沒有出現突變的情況，避免了機器人運動過程中腿部產生振動沖擊的情況，試驗結果驗證了仿真結果的合理性與可行性，達到預期的效果。采用5次NURBS曲線插值法構造的足端軌跡能夠使六足機器人腿部運動平穩、動作快速。