例談直角四面體性質的探究和證明

李小蛟 楊世卿 張 強

(四川省成都市樹德中學 610091)

定義如圖1，四面體O-ABC滿足：OA，OB，OC兩兩垂直，則稱此四面體為直角四面體.

直角四面體有很多性質，而更有意義的是探討性質的過程.

為探究方便，不妨設OA=a,OB=b,OC=c.

探究1由其定義可以直接得到下面性質.

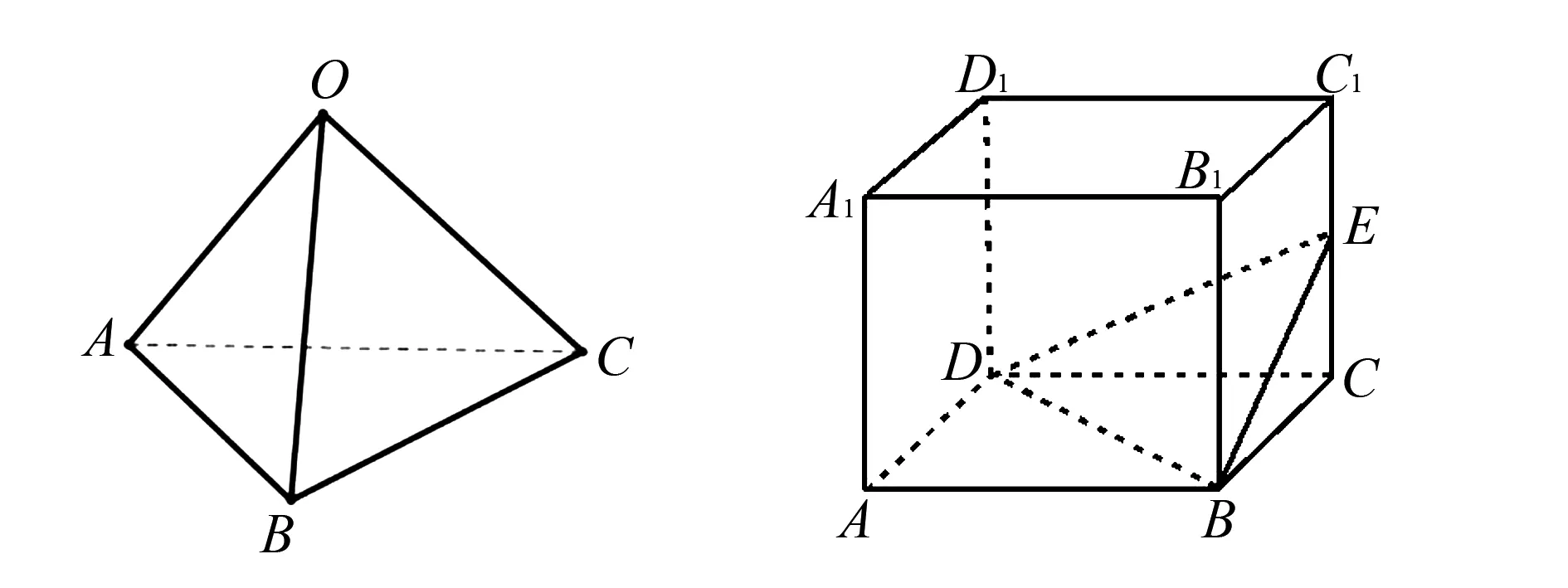
圖1 圖2

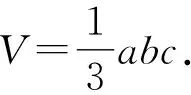
例1(2019年江蘇9)如圖2，長方體ABCD-A1B1C1D1的體積是120，E為CC1的中點，則三棱錐E-BCD的體積是____.

解析由性質1可知

性質2△ABC一定為銳角三角形.

證明因為

所以∠ABC為銳角.

所以∠BCA,∠CAB為銳角.

所以△ABC為銳角三角形.

例2已知直角四面體O-ABC中，O為直角頂點，α,β,λ分別為△ABC的三個內角，求證：cosα·cosβ·cosλ>0.

圖3

解析由上述性質2顯然成立.

探究2將其補成長方體(如圖3)，我們可以得到如下性質.

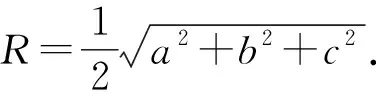
證明補成的長方體和三棱錐有相同的外接球，其外接球直徑為長方體的對角線，

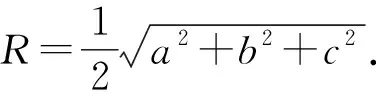
例3已知一直角四面體O-ABC的外接球半徑為定值R，試求其體積的最大值.

即4R2=a2+b2+c2為定值.

由均值不等式,得

探究3過頂點O向平面ACB作垂線，垂足為點H，并過點H作HE⊥AB，垂足為點E，我們可以得到如下性質.

性質4 點H是△ABC的垂心.

證明因為OA⊥OB,OA⊥OC,所以OA⊥平面OBC.所以OA⊥BC.又因為OH⊥平面ABC，所以HA是OA在平面ABC內的射影.

所以由三垂線定理的逆定理知HA⊥BC.

同理可證HB⊥AC,HC⊥AB.

所以點H是△ABC的垂心.

證明因為OC⊥OA,OC⊥OB,所以OC⊥平面OAB，所以OC⊥OE.

如圖4，在Rt△OEC中，OE2=EH·EC.

圖4

從而有

此性質可以由二維空間中的射影定理類比推廣得到，這種由二維空間到三維空間類比的思想是立體幾何中的重要思想，我們再看下面性質.

證明因為

例4已知直角四面體O-ABC的三條直角棱的長分別為OA=a,OB=b,OC=c，求直角面OAB在斜面ABC上的射影面積.

解析由性質5，圖4知

證明因為此直角四面體的體積

又由性質6知

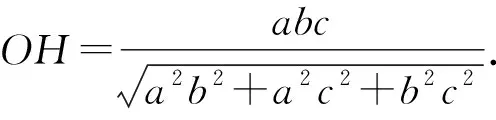
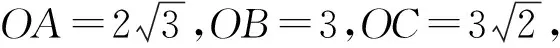
解析由圖4知，點H為△ABC的垂心，所以AB⊥面OEC.

又在Rt△OEC中，

探究4利用上面的等體積法，我們還可以求得此直角四面體的內切球半徑.

證明設內切球球心為I，則

V=VI-OAB+VI-OBC+VI-OCA+VI-ABC

性質9此直角四面體的內切球半徑

證明因為

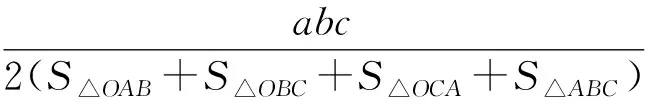
即證

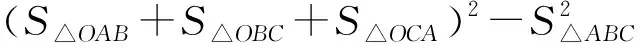
由性質6，上式

=2S△OAB·S△OBC+2S△OBC·S△OCA+2S△OAB·S△OCA

從而得證.

例6 (天津預賽題)已知正三棱錐的側面是面積為1的直角三角形，求它內切球的體積.

解析由性質9知，內切球半徑

性質10直角四面體O-ABC中,設面OBC與面ABC所成的角為α，面OCA與面ABC所成的角為β，面OAB與面ABC所成的角為γ，則cos2α+cos2β+cos2γ=1.

證明如圖4,顯然γ=∠OEC，

所以cos2α+cos2β+cos2γ

即cos2α+cos2β+cos2γ=1.

例7三棱錐O-ABC中，OA,OB,OC三條側棱兩兩互相垂直，其中面OAB、面OBC與面ABC所成的二面角分別為45°和60°，求側面OAC與底面ABC所成的二面角大小.

解析由性質10知，

cos2α+cos245°+cos260°=1，

解得α=60°.

性質11直角四面體O-ABC中,P是面ABC內任意一點，設∠OAP=α,∠OBP=β，∠OCP=γ，則cos2α+cos2β+cos2γ=1.

證明回到探究2補長方體的方法：將直角四面體O-ABC補成一個以OA,OB,OC邊所在直線為長、寬、高所在直線，且OP所在直線為體對角線所在直線的長方體即可得證.

例8 (湖南競賽)O-ABC是三條棱兩兩互相垂直的三棱錐，P為底面ABC內一點，若∠OAP=α，∠OBP=β，∠OCP=γ，求tan2α·tan2β·tan2γ的取值范圍.

解析由性質11知，

sin2α=1-cos2α=cos2β+cos2γ≥2cosβ·cosγ.

同理可得

sin2β=1-cos2β=cos2α+cos2γ≥2cosα·cosγ.

sin2λ=1-cos2λ=cos2α+cos2β≥2cosα·cosβ.

上述三個式子相乘,得

tan2α·tan2β·tan2γ≥8.

從以上直角四面體性質的探究過程中我們發現，基本元素分析和作圖是解決立體問題的基礎(探究1和3)，而長方體是三維空間中標準的模型，構造長方體模型是解決立體幾何問題的有力方法(探究2)，二維到三維空間的類比會助我們在探究立體幾何問題中插上騰飛的翅膀(性質5到性質11).