單擺球在橫向有心力作用下的穩定條件分析
——兼談2021年上海市高考選擇性考試物理卷第17題成立的條件

張懷華

（焦作市第十一中學，河南 焦作 454000）

1 引言

共點力作用下物體的平衡條件、萬有引力定律、單擺振動規律、數學近似運算和物理學史均為高中物理教學的重要內容，亦是高考命題的熱點.2021年上海市高考選擇性考試物理卷第17題就是一道將上述知識點相互滲透、有機融合的創新型試題.

例題.（2021年上海市高考選擇性考試物理卷第17題）測量引力常量G的實驗裝置如圖1所示，小球（可視為質點）處于靜止狀態，擺線偏離豎直方向一個小角度θ0，兩球心之間的距離為r.當質量為M的均勻圓球突然快速移開后，小球的運動________（填寫“可以”或“不可以”）視為簡諧運動.若測出兩球心距r0、圓球質量M、小球偏離豎直方向的水平距離d和小球擺動的周期T，則引力常量G可以表示為________.（當θ0很小時，sinθ0≈tanθ0）

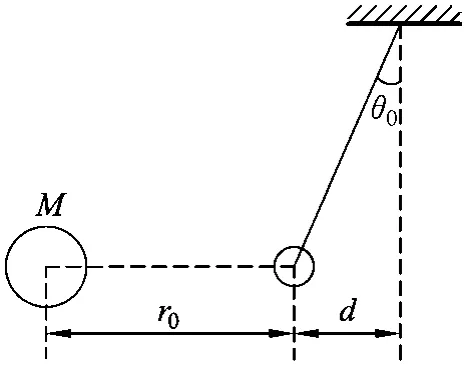
圖1

該題的物理情景十分新穎，考查的范圍也比較全面，側重于對學生模型建構和推理分析等高階思維品質的考查，綜合性較強，難度偏大.

筆者帶領學生們對該題進行深入分析和研究后發現，單擺球在如圖1所示的位置有可能處于不穩平衡狀態，從而在微擾作用下失去穩定.為了確保試題命制的科學性，必須附加r0＞2d的限制條件.

2 單擺球在橫向有心力作用下的穩定條件分析

大量的文獻資料顯示，物體在遵循平方反比規律的有心引力和線性彈簧的共同作用下，物體處于穩定平衡狀態的條件十分苛刻，稍有不慎，物體就會失去平衡.［1-6］因此，很多相似的實際問題都是建立在單擺球在橫向有心斥力作用下保持穩定的情形下的.［7-8］

鑒于2021年上海高考選擇性考試物理卷第17題的物理情景是單擺球在橫向萬有引力作用下的平衡，而單擺球在小擺角條件下的擺線拉力的水平分力與偏移量成正比，則單擺球在橫向有心引力作用下處于穩定平衡狀態的條件十分苛刻，極易在微擾作用下失去平衡.

2.1 單擺球在橫向引力作用下的穩定條件分析

如圖2所示，如果單擺球在大質量球M的引力作用下向左偏θ0角后保持靜止狀態，則由能量最低原理可知，單擺球在左偏角θ0位置的總勢能Ep必須具有極小值.［10，11］

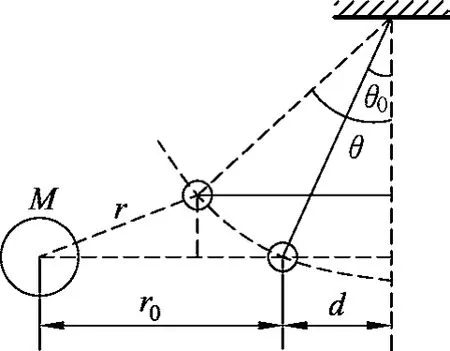
圖2

為了確保單擺球在左偏角θ0位置處的總勢能具有最小值，就必須尋找總勢能Ep與左偏角θ的函數關系.

2.1.1 單擺球總勢能與左偏角的關系式

由力的平衡條件可得

由三角知識可知，單擺球的擺線長度為

若設單擺球向左偏離豎直方向的角度為θ，則單擺球與大質量球M的距離為

由萬有引力勢能公式可知［12，13］

這里以無窮遠處為引力勢能零點.

由（1）-（4）式可得

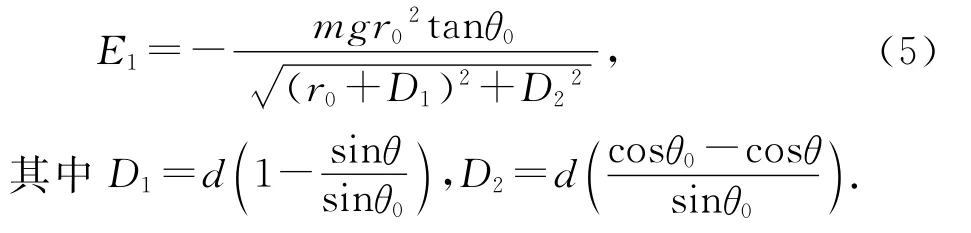
單擺球具有的引力勢能為

以擺球最低點為重力勢能零點.

由（2）、（6）式可得

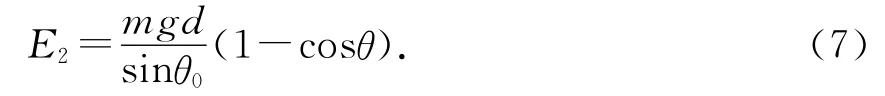
由（5）、（7）式可得，單擺球具有的總勢能為

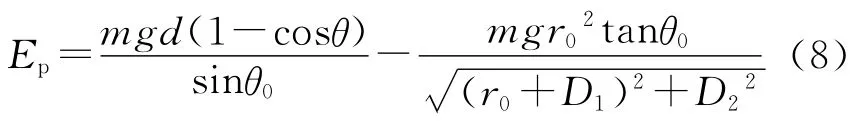
2.1.2 單擺球在左偏角θ0位置處的平衡類型分析

若單擺球在左偏角θ0位置處于穩定平衡狀態，其總勢能Ep對左偏角θ在左偏角θ0位置的一階導數必須等于0，同時二階導數必須大于0.

對（8）式在左偏角θ0位置求一階導數，可得

對（8）式在左偏角θ0位置求二階導數，可得

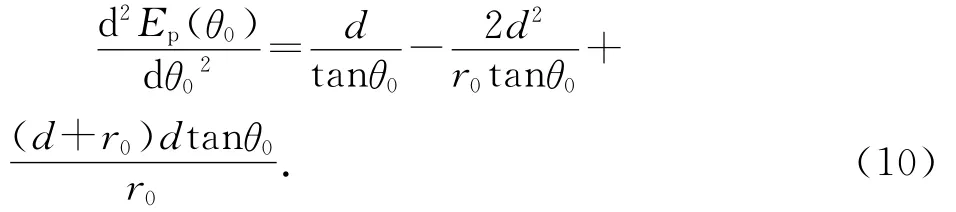
令（10）式大于0，可得單擺球在左偏角θ0位置處于穩定平衡狀態的條件為

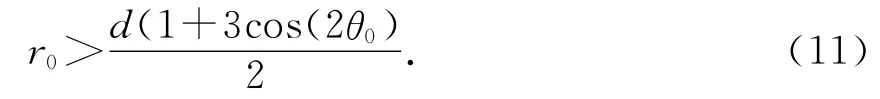
若令左偏角θ0→0，則（11）式可簡化為

在幾何畫板軟件中分別繪制（8）式在r0＞2d和r0＜2d條件下的函數圖像如圖3和圖4所示.

圖3 r0＞2d

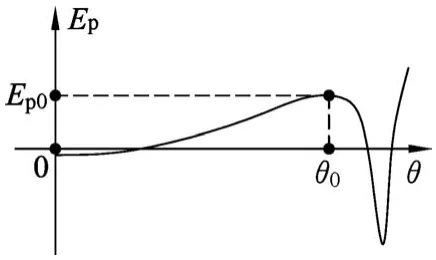
圖4 r0＜2d

對比圖3和（9）、（11）、（12）式可以發現，當單擺球與大質量球之間的距離r0＞2d時，單擺球在θ0位置的總勢能存在如圖3所示的極小值，可以在如圖1所示的左偏角θ0位置處于穩定平衡狀態.

對比圖4和（9）、（11）、（12）式可以發現，當單擺球與大質量球之間的距離r0＜2d時，單擺球在θ0位置的總勢能存在如圖4所示的極大值，無法在如圖1所示的左偏角θ0位置處于穩定平衡狀態.

2.2 單擺球在橫向引力作用下的穩定條件分析

既然單擺球在如圖1所示的有心引力作用下在左偏角θ0處可能失穩，那么單擺球能否在如圖5所示的有心斥力作用下在右偏角θ0處保持穩定呢？

圖5

為了分析單擺球在右偏角θ0處的平衡類型，不妨設單擺球向右偏離最低點的角度為θ，則由勾股定理可得，單擺球與點電荷M的距離為

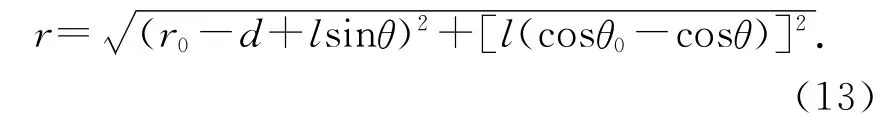
由同種電荷的電勢能公式可知［12，13］

由于單擺球在右偏角θ0處合力為0，則有

由（7）、（13）-（15）式可得，單擺球在斥力作用下右偏θ角時的總勢能為

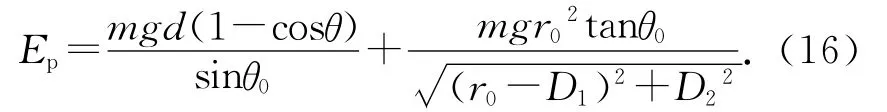
若單擺球在右偏角θ0位置處于穩定平衡狀態，單擺球的總勢能Ep在θ0位置的一階導數必須等于0，同時二階導數必須大于0.

對（16）式在右偏角θ0位置求一階導數，可得

對（16）式在右偏角θ0位置求二階導數，可得

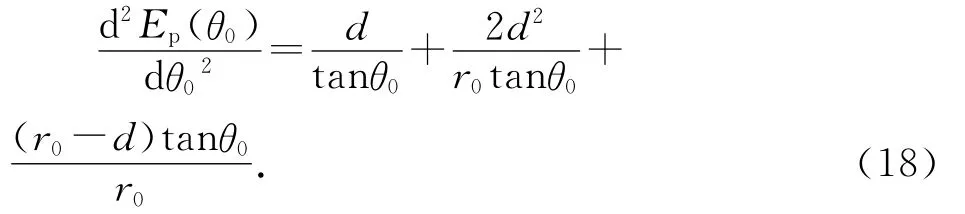
由圖5可知，r0＞d，則由（18）式可知

由（17）、（19）式可知，單擺球在右偏角θ0位置處于穩定平衡狀態.

在幾何畫板軟件中繪制（16）式的函數圖像如圖6所示.由圖6可知，在點電荷的靜電斥力作用下，單擺球的總勢能Ep在右偏角θ0處存在極小值，也說明單擺球在右偏角θ0位置處的平衡類型屬于穩定平衡.

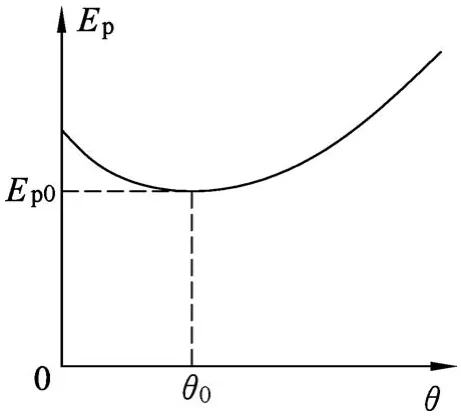
圖6

3 結論

綜上所述，豎直懸掛的單擺球在大質量球的萬有引力作用下偏離平衡位置時，只有當單擺球與大質量球的距離大于單擺球偏離豎直線的距離的2倍時，單擺球才能在與大質量球的引力作用下保持穩定；當單擺球與大質量球的距離不大于單擺球偏離豎直線的距離的2倍時，單擺球無法在大質量球的引力作用下保持穩定.

在以橫向庫侖力（或萬有引力）作用下的單擺球為背景命制創新型試題時，建議選擇斥力類型；若要選擇引力類型，則應該添加“單擺球與引力源的距離大于單擺球偏離豎直線的距離的2倍”的限制條件，保證單擺球能處于穩定平衡狀態.

由上述分析可知，2021年上海市高考選擇性考試物理卷第17題應該追加r0＞2d的限制條件.