二項分布與超幾何分布模型識別問題

陳澤剛 杜海洋

(四川省成都經濟技術開發區實驗中學校)

在教材和考題中常涉及二項分布與超幾何分布，有時，學生不能很好地理解這兩種模型的定義，一遇到“取”或“摸”的題型，就認為是超幾何分布，不加分析，濫用公式，運算對象不明晰.事實上，超幾何分布和二項分布確實有著密切的聯系，但也有明顯的區別，下面筆者通過對兩種分布進行分析并舉例加以說明.

1 基本概念

1.1 超幾何分布

一般地，在含有M件次品的N件產品中，任取n件，其中恰有X件次品，則事件{X＝k}發生的概率為

其中，m＝min{M，n}且n≤N，M≤N.n，M，N∈N*為超幾何分布，如果一個變量X的分布列為超幾何分布列，則稱隨機變量X服從超幾何分布，且

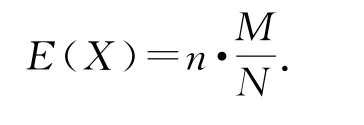
1.2 二項分布

在n次獨立重復試驗中，設事件A發生的次數為X，在每次試驗中，事件A發生的概率為P，那么在n次獨立重復試驗中，事件A恰好發生k次的概率為

此時稱隨機變量X服從二項分布.記作:

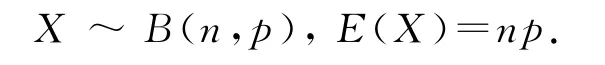
1.3 “二項分布”與“超幾何分布”的聯系與區別

1)“二項分布”所滿足的條件:在每次試驗中，事件發生的概率是相同的;是一種有放回抽樣，各次試驗中的事件是相互獨立的;每次試驗只有兩種結果，事件要么發生，要么不發生;隨機變量是這n次獨立重復試驗中事件發生的次數.

2)“超幾何分布”的本質:在每次試驗中某一事件發生的概率不相同，是不放回抽樣.當樣本容量很大時，超幾何分布近似于二項分布.

3)“二項分布”和“超幾何分布”是兩種不同的分布，但其期望是相等的，即把一個分布看成是“二項分布”或“超幾何分布”時，它們的期望是相同的.事實上，對于“超幾何分布”，若則

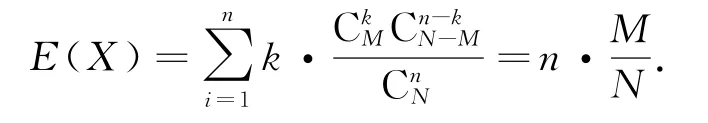
“超幾何分布”和“二項分布”的這種“巧合”，使得“超幾何分布”期望的計算大大簡化.

共同點:每次試驗只有兩種可能的結果:事件發生或事件不發生.

不同點:a)超幾何分布是不放回抽樣，二項分布是有放回抽樣.b)超幾何分布需要知道總體的容量，二項分布不需要知道總體容量，但需要知道“成功率”.

聯系:當總體的容量很大時，超幾何分布近似于二項分布.

2 典型例題

例1袋中有8個白球和2個黑球，從中隨機連續抽取3次，每次取1個球.求:

(1)有放回抽樣時，取到黑球的個數X的分布列;

(2)不放回抽樣時，取到黑球的個數Y的分布列.

解析

(1)有放回抽樣時，取到的黑球個數X可能的取值為0，1，2，3.又由于每次取到黑球的概率均為次取球可以看成3次獨立重復試驗，則所以

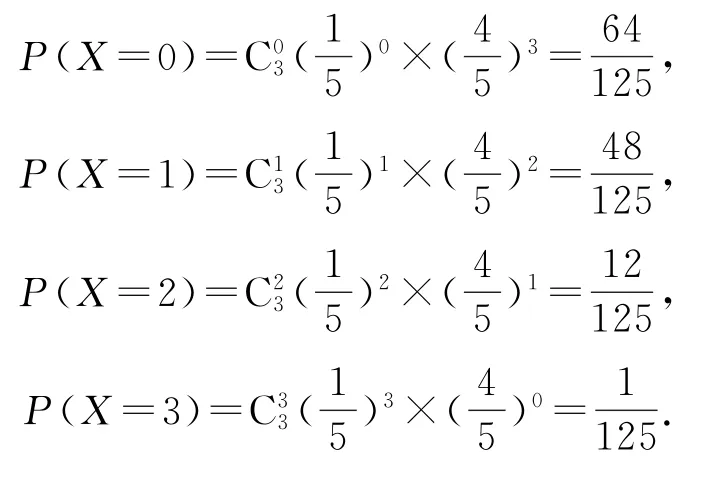
因此，X的分布列如表1所示.

表1

(2)不放回抽樣時，取到的黑球個數Y可能的取值為0，1，2，且有

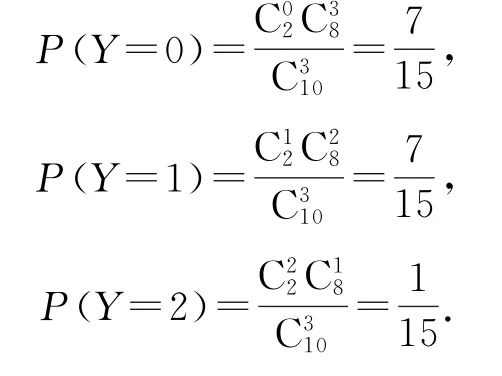
因此，Y的分布列如表2所示.

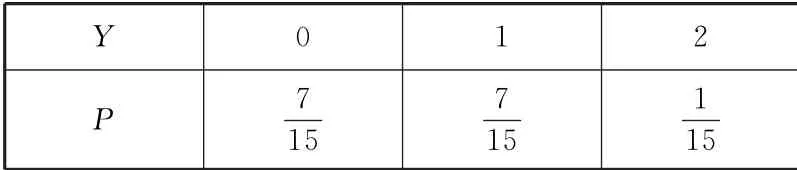
表2

點評

利用兩種分布的不同點，即超幾何分布是不放回抽取，二項分布是有放回抽取，容易使問題獲解.

例2在10件產品中，有3件一等品，4件二等品，3件三等品，從這10件產品中任取3件，求:

(1)取出的3件產品中一等品件數多于二等品件數的概率;

(2)記X表示“取出的3件產品中一等品件數多于二等品件數的數量”，求X的分布列并求E(X).

解析

由題可知:從10件產品中分別任取兩次得到一等品或二等品的概率是不相等的，這是一種不放回抽樣，隨機變量X服從超幾何分布.

(1)設取出的3件產品中一等品件數多于二等品件數為事件A，記事件A1:取出3件一等品;事件A2:取出2件一等品和1件三等品;事件A3:取出1件一等品和2件三等品.由于A1，A2，A3互斥，且A＝A1∪A2∪A3，即

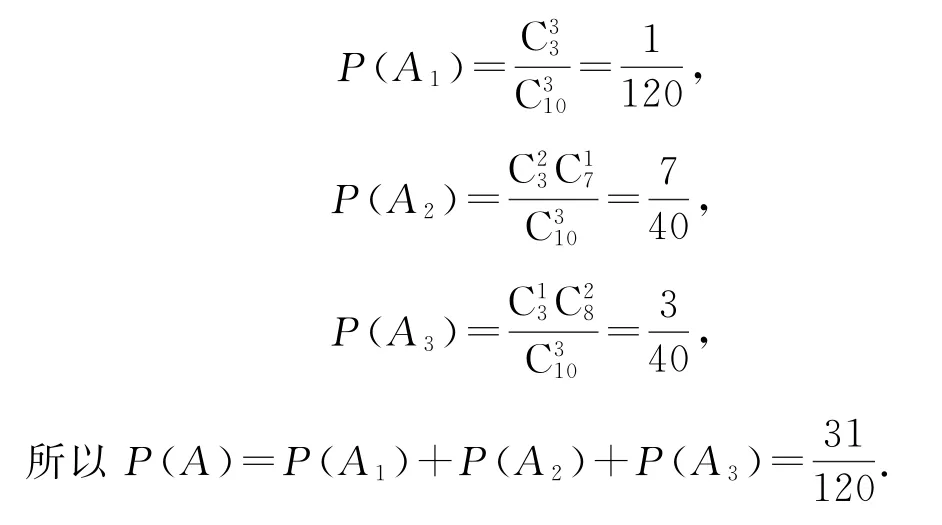
(2)X＝0，1，2，3;X服 從 超 幾 何 分 布，所 以P(X＝0)＝P(1件 一 等 品，1件 二 等 品，1件 三等品)(2件一等品，1件二等品)(3件一等品，1件二等品)(3件一等品，0件二等品)

因此，X的分布列如表3所示.

表3

點評

謹防錯誤地認為隨機變量X服從二項分布，即

例3從某高中學校隨機抽取16名學生，經校醫檢查得到每位學生的視力，其中“好視力”4人，用這16人的樣本數據來估計整個學校的整體數據，若從該校(人數很多)任選3人，記X表示抽到“好視力”學生的人數，求X的分布列及數學期望.

解析

本題就是從“該校(人數很多)任選3人”，由此得到“好視力”人數X，若每次從該校任取一名學生為“好視力”這一事件的概率顯然是相等的，因為該校“人數很多”相當于“有放回抽樣”，因此，隨機變量X服從二項分布而不是超幾何分布.

由題可知X＝0，1，2，3，由樣本估計總體，每次任取一人為“好視力”的概率為則X～B(3，所以

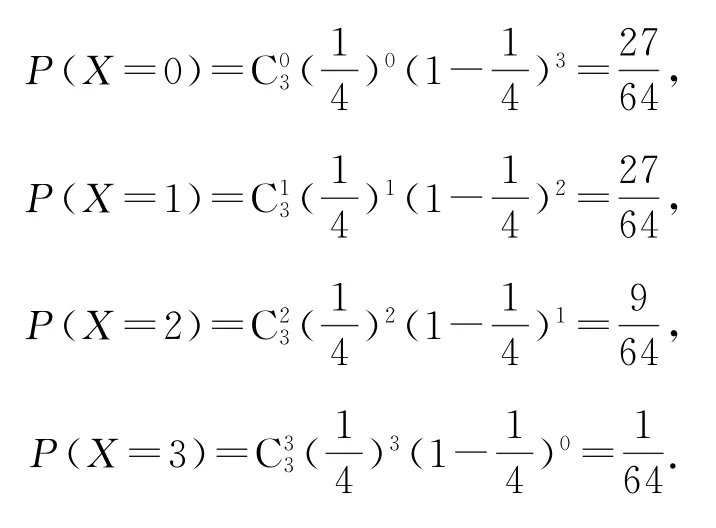
因此，X的分布列如表4所示.

表4

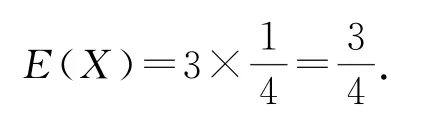
點評

假設問題變為:“從16名學生中任取3名，記X表示抽到‘好視力’學生的人數，求X的分布列及數學期望.”那么X服從超幾何分布，即(X＝0，1，2，3)，其中，數學期望值不變，即

例4寫出下列離散型隨機變量的分布列，并指出其中服從二項分布的是哪些?服從超幾何分布的是哪些?

(1)X1表示n次重復拋擲1枚骰子出現點數是3的倍數的次數;

(2)有一批產品共有N件，其中M件為次品，采用不放回抽取方法抽n件，出現次品的件數為X2(N－M＞n＞0).

解析

(1)X1的分布列如表5所示.

表5

(2)X2的分布列如表6所示.

表6

因此，即X2服從超幾何分布.

點評超幾何分布的抽樣是不放回抽取，各次抽取不獨立，二項分布的抽樣是有放回抽取，各次抽取相互獨立.當超幾何分布所對應的總體數量很大時可以近似地看作二項分布.

通過以上幾例得出，二項分布模型和超幾何分布模型最主要的區別在于是有放回抽樣還是不放回抽樣.因此，在解有關二項分布和超幾何分布問題時，仔細閱讀、辨析題目條件是非常重要的.