抓基礎 理題型 保5分

胡全勇

(西北師大育才學校)

二項式定理在2020年人教A版新教材中，被排在《選擇性必修第三冊》.它在整個高中數學中占比較低，不是高中數學重點教學內容，在高考命題中有時出現，有時不出現.2021年高考四套全國卷(全國甲、乙卷理科，全國新高考Ⅰ，Ⅱ卷)都沒有命題出現，但北京卷、天津卷、浙江卷、上海卷(夏季高考)都有命題出現，因此在2022年高考中應該引起大家足夠重視，雖然屬于簡單題，但是千萬不能“大意失荊州”，做到穩拿5分.

(a＋b)n＝＋b＋…＋＋…＋(n∈N*)是二項式定理，右邊的多項式是二項展開式，其中(k＝0，1，2，…，n)是二項式系數(特別需要強調的是，有關二項式運算時，要厘清二項式系數與所求系數的區別與聯系，不能混為一談)，將二項展開式中的第k＋1項，即n，k∈N*)稱為二項展開式的通項(或通項公式).學好二項式定理，必須做到如下幾點.

1 熟練運用通項公式求特定項

在運用通項公式求二項展開式的特定項(一般指展開式的常數項、x的幾次方項、有理項)時，為了運算方便，常常將未知數是根式的項寫成分數指數冪，未知數是分式的項寫成負整數指數冪，二項式中間為減號時，將減號與第二項結合，這類試題是高考命題中二項式定理部分考查頻率最高的內容.

1.1 求常數項

求常數項是與二項式有關的試題出現頻率最高的一個知識點，基本方法一般為運用通項公式將展開式中的第k＋1項整理為系數與未知數兩部分乘積的形式，然后令未知數的指數為零，得到相應的k值，從而寫出該項，這即為所求常數項.

例1(2021年北京卷11)的展開式中常數項是________.

解析

(x3－展開式的通項公式為

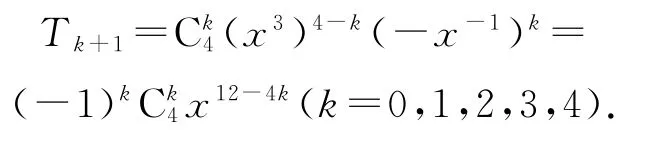
令12－4k＝0，則k＝3，故所求常數項為

例2(2018年浙江卷理14)二項式的展開式的常數項是________.

解析

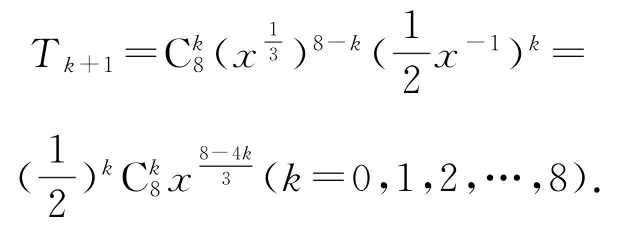
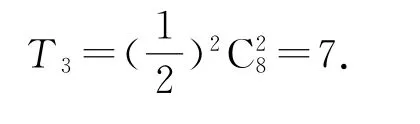
點評

這兩道求常數項的題目，屬于非常基礎的題，也是高考的常見題型，求解要點是運用通項公式時按照要求運算.

1.2 求x的幾次方項

求x的幾次方項是與二項式有關的命題中比較常現的一個知識點，基本方法一般為運用通項公式將展開式中的第k＋1項整理為系數與未知數兩部分的乘積，然后令未知數的指數為所求的未知數x的指數(如求x3項，就可以令未知數的指數等于3)，得到相應的k值，從而寫出所求項(注意:有時求的是該項的系數).

例3(2021年上海卷6)(x＋a)5的展開式中，x2的系數為80，則a＝________.

解析

(x＋a)5的 通 項 公 式 為Tk＋1＝(k＝0，1，…，5).令5－k＝2，則k＝3，所以a3＝80，解得a＝2.

例4(2018年全國Ⅲ卷理5)的展開式中x4的系數為( ).

A.10 B.20 C.40 D.80

解析

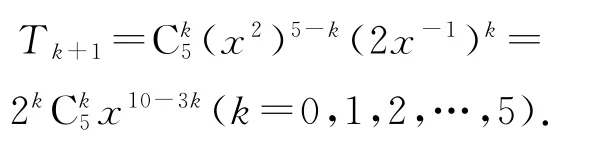
令10－3k＝4，則k＝2，所以展開式中x4的項為即x4的系數為40.故選C.

點評

這兩道題均是通項公式的基本運用，屬于基礎題，要避免失分.

1.3 有理項問題

求有理項是與二項式有關的問題出現頻率較低的一個知識點，求解的基本方法一般為運用通項公式將展開式中的第k＋1項整理為系數與未知數兩部分的乘積，然后令未知數的指數為整數(這樣的項，一般不只一項，需要分類討論)，得到相應的k值，從而寫出對應的項.

例5已知的展開式中，前三項系數的絕對值依次構成等差數列.

(1)證明:展開式中沒有常數項;

(2)求展開式中的所有有理項.

解析

依題意可得n≥2，又因為前三項系數的絕對值依次構成等差數列，即

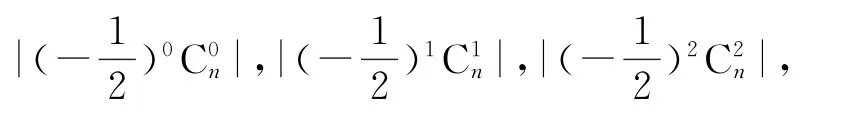
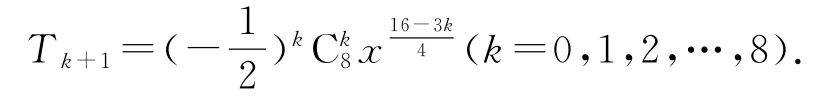
假設展開式中的第k＋1項為常數項，則0，解得，所以假設不成立，故這個展開式中沒有常數項.

(2)由(1)可得求通項公式為則展開式中三項有理項，分別為

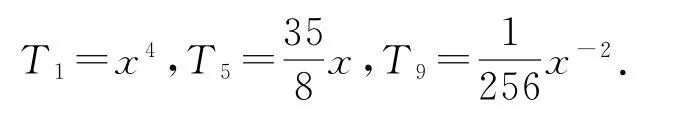
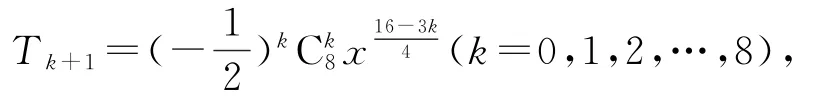
點評

展開式中的有理項是指未知數x的指數為整數的項，這個展開式中由于x的指數為所以求有理項時，k必須取4的倍數.

2 掌握三項式或兩項乘積問題的運算技巧

2.1 三項式問題

1)底數為完全平方式

求底數為三項，并且底數為完全平方式的基本方法:將底數整理成一個完全平方式的形式，運用(an)m＝amn的運算法則，將底數整理成為兩項，再運用二項式定理求解.

例6的展開式中x2項為_____.

解析

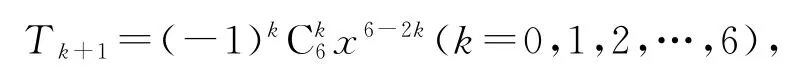
令6－2k＝2，則k＝2，故展開式中x2的項為

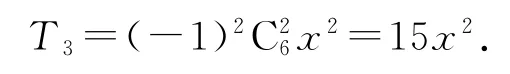
點評

解答這道題時注意兩點:其一，底數是一個完全平方式;其二，求的是含有x2的項，而不是系數.

2)底數可以分解成兩個因式乘積的形式

求底數為三項，并且底數可以分解成兩個因式乘積的形式的基本方法:將底數分解因式后運用(ab)n＝anbn寫成兩個二項式的積，如果兩項的指數不太高，可以直接將兩個二項式展開，根據多項式乘法完成;如果兩項的指數比較高，再分別根據二項式展開式的通項公式進行討論，這樣比較復雜.

例7(x2＋3x＋2)3的展開式中x4的系數為________.

解析

因為

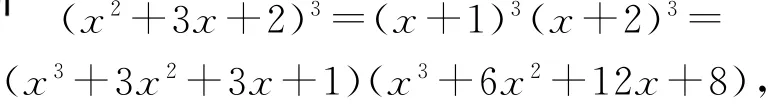
所以展開式中含有x4的項為12x4，18x4，3x4，故展開式中x4的項系數為33.

點評

這道題底數可以分解成兩個因式乘積的形式，所以問題可以轉化為兩個冪式乘積問題，又由于展開式次數較低，所以可以直接展開，然后運用多項式乘法;如果冪指數較大，則分別運用通項公式，再結合多項式乘法.

3)把其中的兩項看成一項，連續用通項公式

求底數為三項，并且底數不能分解成兩個因式乘積的形式的基本方法:將其中的某兩項看成一項(一般都是含有兩個未知數，這樣將兩個未知數分開看成兩項)，然后運用二項式展開式展開，按照題目要求，確定相應的常數，再進行討論.

例8(2015年全國Ⅰ卷理10)(x2＋x＋y)5的展開式中，x5y2的系數為( ).

A.10 B.20 C.30 D.60

解析

(x2＋x＋y)5＝[(x2＋x)＋y]5的通項公式為Tk＋1＝Ck5(x2＋x)5－kyk(k＝0，1，2，…，5)，在展開式中令k＝2，則C25(x2＋x)3＝C25[(x2)3＋3(x2)2x＋3x2x2＋x3]，故x5y2的系數3C25＝30.故選C.

點評

底數既不是完全平方式又不能因式分解，解題時只能把某兩項看成一項，到底將哪兩項看成一項，要視題設而定，本題把含有x的看成一個整體運算比較方便.

2.2 兩項乘積問題

求兩個二項式乘積問題的一般方法為，如果兩項中一項指數較低(一般為一次或二次)，另一項指數較高，將指數較低的項不動(二次就直接展開)，寫出指數較高項的通項公式，運用多項式乘法討論;若兩項的指數都較高，則可以將兩項都展開根據多項式乘法討論，或都寫出通項分類討論.

例9(2019年全國Ⅲ卷理4)(1＋2x2)(1＋x)4的展開式中x3的系數為( ).

A.12 B.16 C.20 D.24

解析

方法1(1＋2x2)(1＋x)4＝(1＋2x2)(1＋4x＋6x2＋4x3＋x4)，所以展開式中x3的系數為1×4＋2×4＝12.故選A.

方法2因為(1＋x)4的通項公式為

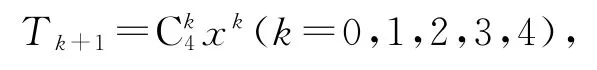
所以展開式中x3的項為

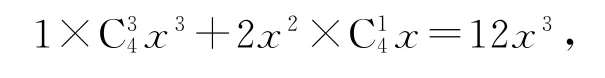
所以x3的系數為12.故選A.

3 會用二項式定理解決整除問題

運用二項式定理解決整除問題在近幾年高考中出現的次數很少，但是教材習題中有出現，作為二項式定理的一個知識點，還是有必要掌握這類問題的求解方法，解決這類問題的基本思路是將底數湊成除數的和或差的形式，然后運用二項展開式展開.

例10若是11的倍數，則自然數n為( ).

A.被3除余1的數 B.偶數

C.3的倍數 D.奇數

解析

是11的倍數，所以n＋1為偶數，n為奇數.故選D.

例11若n是正整數，則7n＋7n－1Cn1＋7n－2·Cn2＋…＋7除以9的余數是_________.

解析

因為n是正整數，7n＋7n－1＋…＋＝(7＋1)n－＝8n－1＝(9－1)n－1＝(－1)0＋(－1)1＋…＋·(－1)n－1＋(－1)n－1，則除以9時，若n為偶數，余數為0;若n為奇數，余數為7.

點評

根據這個式子不能直接將底數湊為9，必須分兩步完成，將底數中的一個湊為9后展開.

4 應用賦值法解決與二項式有關的問題

在關于二項式定理的運算中，有時要求一些項系數的和或差，解決這類問題的基本方法是直接賦值，有時需要根據式子特征先求導，再賦值.

例12設

解析

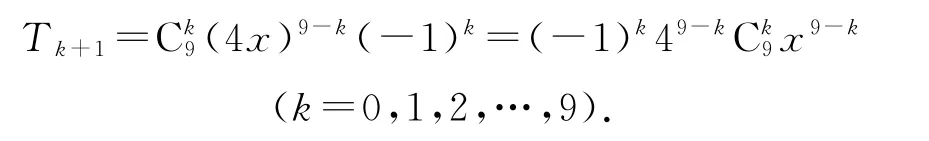
令9－k＝－2，可得k＝11(舍);令9－k＝0，可得k＝9.所以的展開式中的系數為－1，即b＝－1，故

點評

例13若(3－2x)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5，則a0＋a1＋2a2＋3a3＋4a4＋5a5的值為_____.

解析

因為

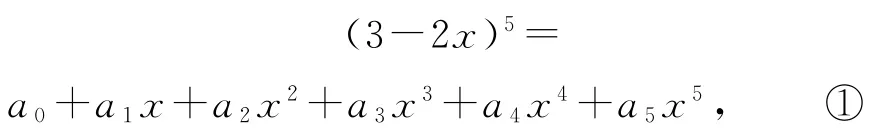
對式①兩端求導數，可得

在①中，令x＝0，可得a0＝35;

在②中，令x＝1，可得a1＋2a2＋3a3＋4a4＋5a5＝－10，所以

點評

求解這道題時先直接賦值求出a0，再對式子兩端求導，最后賦值求出其他剩余的項.

5 關注楊輝三角在數學文化中的應用

解決與楊輝三角有關問題的基本思路:根據楊輝三角每一橫行數的特征、斜列數的特征以及每個數與它肩頭兩個數的關系處理.

例14我國南宋數學家楊輝在所著的《詳解九章算法》一書中用如圖1所示的三角形解釋二項展開式的系數規律，去掉所有為1的項，依次構成2，3，3，4，6，4，5，10，10，5，6，…，則此數列的前50項的和為( ).

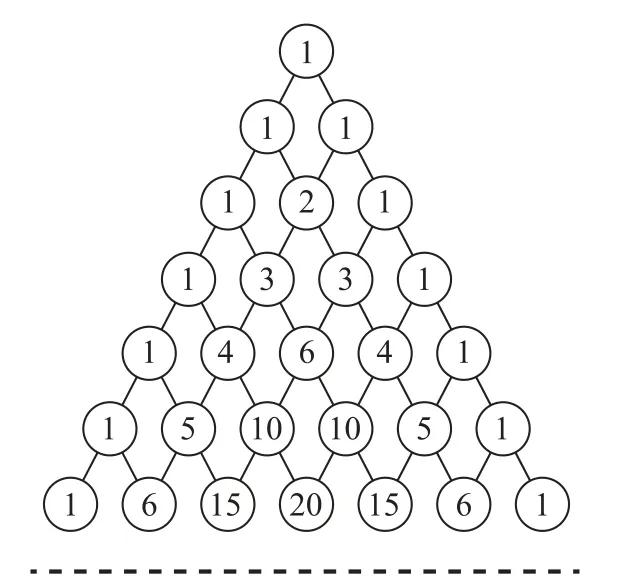
圖1

A.2025 B.3052 C.3053 D.3049

解析

由圖1可知，去除所有為1的項后，前n行共個數，當n＝10時，55，即前10行共有55個數，去除1的項后，第n－1行的和為C1n＋C2n＋…＋Cn－1n＝2n－2，所以前10行的和為212－24＝4072.

點評

解答這道題巧妙地運用了楊輝三角形的性質，即第n行(a＋b)n的展開式的各項的二項式系數依次為

總之，解決二項式定理問題要熟練掌握基本公式，善于發現和總結規律，從而找到解決問題的最佳途徑.

鏈接練習

1.(2021年上海卷春季7)已知(1＋x)n的展開式中，唯有x3的系數最大，則(1＋x)n的系數和為_________.

2.(2021年上海卷夏季6)已知二項式(x＋a)5的展開式中，x2的系數為80，則a＝_________.

3.(2021年浙江卷13)已知多項式(x－1)3＋(x＋1)4＝x4＋a1x3＋a2x2＋a3x＋a4，則a1＝_________；a2＋a3＋a4＝_________.

A.5 B.10 C.15 D.20

鏈接練習參考答案

1.64.2.2.3.5；10.4.C.