二項式定理相關問題常見題型與處理策略

郭興甫

(云南省會澤縣東陸高級中學 云南萬人計劃教學名師張國坤研修工作坊)

二項式定理是高中數學新舊教材中的重要內容.在高中數學課程中，二項式定理安排在計數原理、排列組合知識之后，隨機變量及其分布列之前，它既是計數原理和組合知識的應用，又是探究相關概率公式的基礎，是培養數學運算素養的重要載體，也是高考命題的熱點內容.幾乎每年的高考試題都有涉及，一般以選擇題、填空題的形式出現，難度中等偏下，是高考容易得分的試題.為了幫助廣大師生更好地復習這部分內容，本文以近年全國各地的高考題及模擬試題為例說明二項式定理常見題型及處理策略.

1 求解形如(a+b)n(n∈N*)的展開式中與特定項相關的問題

例1(1)(2019年天津卷理的展開式中的常數項為_________.

A.－210 B.－960 C.960 D.210

解析

(2)依題意得2n＝1024，解得n＝10.又易知展開式的通項為

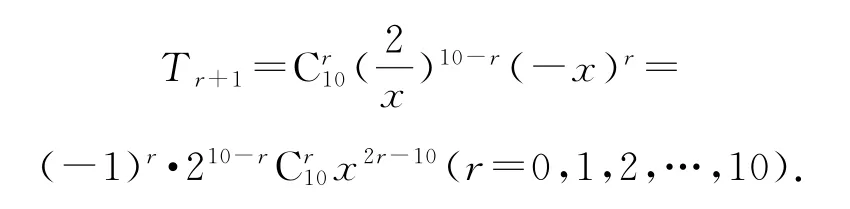
由2r－10＝4，得r＝7，從而有－960，所以x4的系數是－960.故選B.

點評

求解形如(a＋b)n(n∈N*)的展開式中與特定項相關的量的處理策略:先將展開式的通項公式化為只含有一個字母的形式.求展開式中的特定項可依據條件寫出第r＋1項，再根據特定項的特點建立方程求出r的值即可.已知展開式的某項，求特定項的系數，可由某項得出參數項，再由通項寫出第r＋1項，由特定項得出r的值，進而求出參數.

2 求解形如(a+b)m(c+d)n(m，n∈N*)的展開式中與特定項相關的問題

例2(1)已知的展開式中各項系數之和為0，則該展開式的常數項是( ).

A.－10 B.－7 C.10 D.9

A.72 B.60 C.48 D.36

(3)(x＋y)2(x－2y)4的展開式中x2y4的系數為( ).

A.88 B.－24 C.－40 D.104

解析

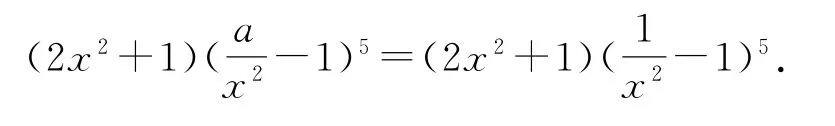
令3－r＝1，得r＝2;令(舍);令3－r＝2，得r＝1.故的展開式中x2的系數為(－2)2C26＋(－2)1×＝60－12＝48.故選C.

(3)由題設，(x＋y)2展開式的通項為Tm＋1＝x2－m·ym，(x－2y)4展 開 式 的 通 項 為Tn＋1＝x4－n(－2y)n，所以原多項式的展開式通項可寫為

點評

求一個多項式與一個二項展開式積的展開式的相關問題，可以先求二項展開式的通項公式，再結合條件確定通項公式中的項使之滿足條件，進而解決問題.求兩個二項展開式積的相關問題，可以先分別用不同的指數表示出兩個二項式的通項公式，再把兩個通項公式的積化為只含一個未知數的通項公式的形式，利用通項公式結合條件建立方程組求出指數值，進而代入通項公式求出相應結果.求幾個二項式積的展開式中的特定項(系數)問題的處理方法，利用二項式展開式計算指定項的系數時，注意利用二項式展開式的通項公式和多項式的乘法判斷出指定項的系數是由哪些項的系數相乘所得到的，進而利用分類加法計數原理求解.

3 求解形如(a+b+c)n(n∈N*)的展開式中與特定項相關的問題

例3(1)(x2＋3x＋2)5的展開式中x2的系數為( ).

A.625 B.800 C.750 D.600

(2)在(x2＋2x＋y)5的展開式中，x5y2的系數為( ).

A.60 B.30 C.15 D.12

A.32 B.－32 C.33 D.－33

解析

(1)方法1(x2＋3x＋2)5＝[(1＋x)(2＋x)]5＝(1＋x)5(2＋x)5，(1＋x)5展開式的通項 為展 開 式 的 通 項 為所以(x2＋3x＋2)5展開式的通項為，其中0≤r≤5，0≤k≤5，且r，k∈N.

令r＋k＝2，可得

因此，(x2＋3x＋2)5的展開式中x2的系數為C05C2523＋C15C1524＋C25C0525＝800，故選B.

方法2因為(x2＋3x＋2)5表示5個因式(x2＋3x＋2)的乘積，它展開式中含x2的項需滿足1個因式取x2，其余因式都取2，或2個因式取3x，其余因式都取2，故(x2＋3x＋2)5的展開式中x2的系數為C1524＋C2532×23＝800，故選B.

(2)方法1(x2＋2x＋y)5＝[(x2＋2x)＋y]5，由通項公式可得Tr＋1＝Cr5(x2＋2x)5－ryr，要求x5y2的系數，故r＝2，此時(x2＋2x)3＝x3·(x＋2)3，其對應x5的系數為C23·x2·21＝6，所以x5y2的系數為C25×6＝60，故選A.

方法2因(x2＋2x＋y)5表示5個因式(x2＋2x＋y)的乘積，故它的展開式中含x5y2的項需滿足2個因式取y，2個因式取x2，1個取2x，故x5y2的系數為C25×C23×2＝60，故選A.

(3)方法1在的展開式中，令x＝1，可得展開式中各項系數和為(1＋2－1)4＝24＝16，展開式的通項為展開式的通項為展開式的通項為且r，k∈N).

令r－2k＝0，可得所以展開式中常數項為因此，展開式中除常數項外，其余各項系數的和為－33，故選D.

方法2表 示4個 因式的乘積，故展開式中的常數項滿足1個因式取x，1個取個取－1，或2個取x，2個 取或4個因式都取－1，即展開式中的常數項為

又各項系數和為(1＋2－1)4＝24＝16，所以展開式中除常數項外，其余各項系數的和為－33，故選D.

(4)根據多項式乘法法則，要得到x8，則在10個因式中需要8個選x，其余兩個選a，或9個選x，1個 選即由題意得(－1)＝170，又a＞0，解得a＝2，故選C.

點評

對于多項式(三項或以上)的n次方的展開式，求特定項的相關問題的處理策略:一是將三項式或多項式轉化為二項式積的形式，然后利用多項式積的展開式中的特定項(系數)問題的處理方法求解;二是將其中某兩項看成一個整體，直接利用二項式定理展開，然后分類考慮產生特定項的所有可能情形，再逐一求出每種情形對應的項，最后合并即可;三是利用二項式定理的推導過程，通過排列組合的兩個原理解決問題，即在多項式的n次方的展開中，可把式子看作n個多項式相乘，乘積的項是由每個多項式中選取一項相乘所得到的.

4 求解二項式展開式各項系數和的問題

例4(1)(x2＋2ax－a)5的展開式中各項的系數和為1024，則a的值為( ).

A.1 B.2 C.3 D.4

(2)已知(x＋2)(2x－1)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5＋a6x6，則a0＋a2＋a4＝( ).

A.123 B.91 C.－120 D.－152

(3)(1＋ax)10(a≠0)的展開式的常數項與其各項系數之和相等，則其展開式中x2的系數為( ).

A.－45 B.45 C.－180 D.180

解析

(1)賦值法:令x＝1，可知展開式中各項系數和(a＋1)5＝1024，解得a＝3，故選C.

(2)方法1令x＝1，得

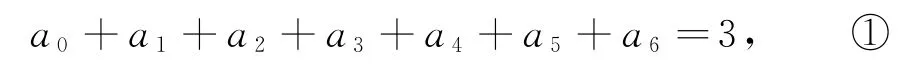
令x＝－1，得

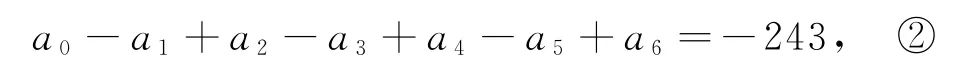
①＋②，得a0＋a2＋a4＋a6＝－120.

又a6為(2x－1)5中25項的系數，所以a6＝C0525＝32，所以a0＋a2＋a4＝－152，故選D.

方法2因為(2x－1)5展開式的通項為Tr＋1＝Cr5(2x)5－r(－1)r(r＝0，1，2，3，4，5)，所以

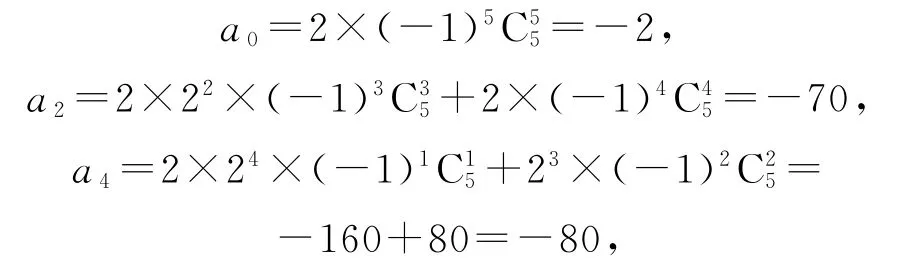
所以a0＋a2＋a4＝－152，故選D.

(3)因(1＋ax)10(a≠0)展開式的通項為

令r＝0，得常數項為1.

令x＝1，得各項系數之和為(1＋a)10，由題意知(1＋a)10＝1，又a≠0，所以a＝－2，所以Tr＋1＝(－2)rCr10xr(r＝0，1，2，…，10)，所以其展開式中x2的系數為故選D.

點評

本題主要考查利用賦值法解決二項展開式中系數和的相關問題，同時考查方程思想和數學運算素養.利用賦值法求展開式各項系數和，對形如(ax＋b)n，(ax2＋bx＋c)n(a，b，c∈R)的式子，只需令x＝1;對形如(ax＋by)n(a，b∈R)的式子，只需令x＝y＝1.若f(x)＝(ax＋b)n＝a0＋a1x＋…＋anxn展開式中的各項系數的和為f(1)，則奇數項的系數和為偶數項的系數和為

5 求解幾個二項式和(或差)的相關問題

例5(1)在(x＋1)3＋(x＋1)4＋(x＋1)5＋(x＋1)6＋(x＋1)7的展開式中x2的系數是( ).

A.45 B.53 C.54 D.55

(2)已 知 多 項 式(x－1)3＋(x＋1)4＝x4＋a1x3＋a2x2＋a3x＋a4，則a1＝_________，a2＋a3＋a4＝_____.

(3)已知(1＋x)m＋(1＋3x)n(m，n∈N*)展開式中x的系數為11，當x2的系數取得最小值時，x4的系數是________.

解析

(1)顯然x≠0，在(x＋1)3＋(x＋1)4＋(x＋1)5＋(x＋1)6＋(x＋1)7＝的展開式中，x2的系數是C38－1＝55，故選D.

(2)(x－1)3＝x3－3x2＋3x－1，(x＋1)4＝x4＋4x3＋6x2＋4x＋1，所以a1＝1＋4＝5，a2＝－3＋6＝3，a3＝3＋4＝7，a4＝－1＋1＝0，則a2＋a3＋a4＝10.

(3)由已知得C1m＋3C1n＝11，即m＋3n＝11，所以m＝11－3n，x2的系數為

當n＝2時，x2系數取得最小值19，則m＝11－3×2＝5，即(1＋x)5＋(1＋3x)2中x4的系數為C45＝5.

點評

幾個二項式和的展開式中的特定項(系數)問題的處理方法:先分別求出每一個多項式中的特定項，再合并.計算時注意利用組合數公式或組合數性質進行簡化.

6 求解二項式系數或項的系數的最值問題

例6(1)設(1＋x)n＝a0＋a1x＋a2x2＋…＋anxn(n∈N*)，若a1＋a2＋…＋an＝255，則展開式中二項式系數最大的項是( ).

A.240x4B.160x3

C.70x4D.20x3

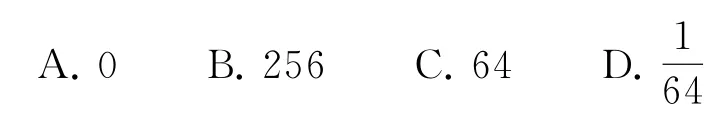
(3)已知(1＋2x)8展開式的二項式系數的最大值為a，系數的最大值為b，則的值為( ).

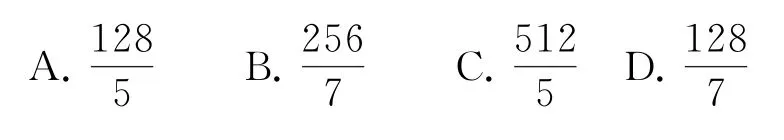
解析

(1)已知(1＋x)n＝a0＋a1x＋a2x2＋…＋anxn，當x＝1時，a0＋a1＋a2＋…＋an＝2n，當x＝0時，a0＝1.所以

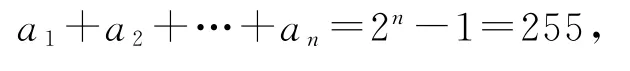
解得n＝8，則(1＋x)8展開式中二項式系數最大為C48，二項式系數最大的項為C48·x4＝70x4，故選C.

(2)因為展開式中只有第4項的二項式系數最大，所以n＝6.令x＝1，則展開式中所有項的系數和是故選D.

(3)由題意可得a＝C48＝70，又(1＋2x)8展開式的通項公式為Tr＋1＝Cr82rxr，設第r＋1項的系數最大，則

點評

解答本題的關鍵在于求解n的值以及確定二項式系數的最大值.求展開式中系數的最大項與求二項式系數最大項是不同的，需要根據各項系數的正、負變化情況進行分析.二項式系數最大項的確定方法:如果n是偶數，則中間一項(第項)的二項式系數最大;如果n是奇數，則中間兩項(第項與第項)的二項式系數相等并最大.求解形如(ax＋by)n(a＞0，b＞0)展開式中系數的最大項，一般采用待定系數法:設展開式中的第r＋1項是系數最大項，其系數記為Ar，則由可求出r的值，從而求出展開式中系數最大的項.

7 利用二項式定理解決整除性問題

例7(1)5555除以8，所得余數是( ).

A.7 B.1 C.0 D.－1

(2)已知742020＋a能夠被15整除，則a的最小正數為_________.

(3)記X＝1－90Cn1＋902Cn2－903Cn3＋…＋(－90)kCkn＋…－90nCnn(n為正奇數)，則X除以88的余數為_________.

解析

(1)5555＝(56－1)55，其展開式的通項為Cr555655－r(－1)r，不能被8整除，即r＝55時，余數為(－1)55＝－1，由于余數要為正數，故加8，得－1＋8＝7.故選A.

(2)由題可知，742020＋a＝(75－1)2020＋a＝，而75能被15整除，要使742020＋a能夠被15整除，只需1＋a能被15整除即可，所以a的最小正數為14.

(3)由組合數的性質知

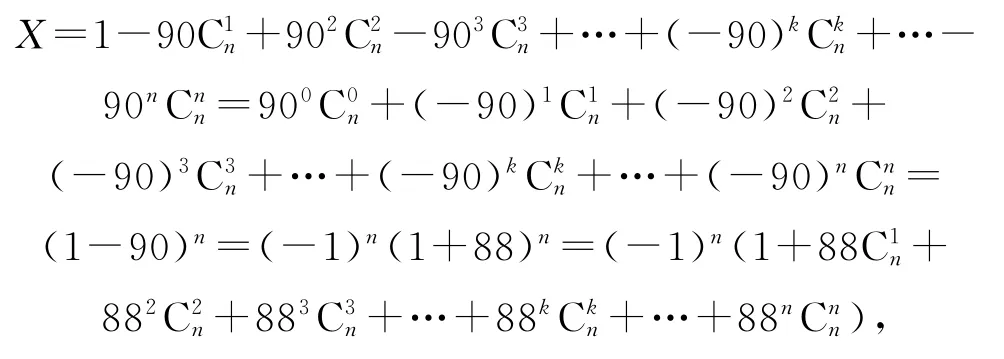
則X除以88的余數為－1＋88＝87.

點評

本題主要考查利用二項式定理解有關整除問題，關鍵在于將原式轉化為除數的倍數再進行展開，即通常先把底數寫成除數(或和除數有密切關系的數)與某數的和或差的形式，利用二項式定理展開，再考慮后面或者前面一、二項進行判斷.解決求余數問題，必須構造一個與題目條件有關的二項式.要注意余數的范圍，對形如m＝pr＋n，其中r是除數(r是正整數)，n是余數，0≤n＜r，利用二項式定理對展開式進行變形后，若剩余部分是負數，則需要轉化為非負數.特別地，余數可以為0，余數為0表示整除.

《普通高中數學課程標準(2017年2020年修訂)》指出“數學運算是指在明晰運算對象的基礎上，依據運算法則解決數學問題的素養”.主要包括:理解運算對象，掌握運算法則，探究運算思路，選擇運算方法，設計運算程序，求得運算結果等.無論是在高中數學解題教學的學習過程中，還是在高考數學復習的教學中，要把發展學生的數學運算能力作為課堂教學的重要任務.高中數學解題教學不但要科學合理地滲透解題策略，還要讓學生掌握知識方法的來龍去脈，感悟其本質，歸納總結解題思路及適用范圍，拓展學生知識視野，以不變應萬變，從而提高解題能力，揭開解題的神秘感.

鏈接練習

A.20 B.－120 C.60 D.－60

2.(x2＋2y)(1＋y－x)5展開式中x3y4的系數是( ).

A.10 B.－5 C.5 D.－10

3.已知(x＋1)6(ax－1)2的展開式中，x3系數為56，則實數a的值為( ).

A.6或－1 B.－1或4

C.6或5 D.4或5

4.設(3x－1)5＝a0＋a1(x－1)＋a2(x－1)2＋a3(x－1)3＋a4(x－1)4＋a5(x－1)5，則a1＋a2＋a4＋a5＝( ).

A.2010 B.2011

C.2012 D.2013

5.(1－2x)5(1＋3x)的展開式中按x的升冪排列的第3項為_________.

6.已知(ax＋1)6的展開式中x3的系數為A，(x－1)(x＋a)6的展開式中x3的系數為B，A＋B＝15，則非零常數a的值為________.

9.已知(1＋2x)n的展開式中，第6項和第7項的二項式系數最大.

(1)求n的值；

(2)求展開式中系數最大的項.

鏈接練習參考答案

1.C.2.B.3.A.4.D.

5.10x2.6.±1.7.481.8.60.

9.(1)n＝11.

(2)展開式中系數最大的項有兩項，即第8項42240x7和第9項42240x8.