基于數學思想引領與素養導向的“概率與統計”復習

巨小鵬

(陜西省漢中市龍崗學校)

自《普通高中數學新課程標準(2017版2020年修訂)》(以下簡稱:新課標)實施以來，對概率與統計這一部分內容的考查變化很大，增刪調整了很多內容，這也標志著對概率與統計這一部分內容的要求更加完善和明確.數學教學中的深度學習就是學生以主動積極的情感，將思維特別是高階思維貫穿到數學學習過程的始終，他們不僅要關注知識技能“是什么”“怎樣用”，還要探究知識技能的來龍去脈.數學思想就是從高階思維角度闡述數學知識的規律和思維邏輯的本質，將數學復習提升到思想方法的層面，以達到深度復習的效果.

1 精準領會新課標要求

1.1 新、舊課標區別分析

對于概率這一部分內容，新課標增加了“理解樣本點和有限樣本空間的含義”“理解概率的性質，掌握隨機事件的運算法則”，強調“了解隨機事件的并、交與互斥的含義，能結合實例進行隨機事件的并、交計算”，增加了“結合有限樣本空間，了解兩個隨機事件獨立性的含義，結合古典概型，利用獨立性計算概率”.

對于統計這一部分內容，新課標增加了“普查和抽查、互聯網獲取數據的途徑”“了解總體、樣本、樣本量的概念，了解數據的隨機性”“會計算樣本均值和樣本方差，了解樣本與總體的關系”，新課標對分層抽樣提出更加細致的要求，要求掌握各層樣本量比例分配的方法和分層隨機抽樣的樣本均值和樣本方差，比舊課標提高了要求.新課標刪除了系統抽樣的方法，增加了“能根據實際問題的特點，設計恰當的抽樣方法解決問題”，進一步凸顯數學知識在解決問題中的作用.新課標強調“能根據實際問題的特點，選擇恰當的統計圖表”，強調了平均數、中位數、眾數均體現數據的集中趨勢，提高了對眾數和中位數的要求，并要求學生理解集中趨勢參數的統計含義，強調了標準差、方差和極差體現數據離散趨勢，提高了對方差和極差的要求，并要求學生理解離散程度參數的統計含義，刪除了對“初步體會樣本頻率分布和數字特征的隨機性”的要求，刪除了對“形成對數據處理過程進行初步評價的意識”的要求，增加了對“能用樣本估計百分位數，理解百分位的統計含義”，對樣本數據的分析提出了新的要求.

1.2 七了解、八理解、三會和五掌握

七了解:隨機事件的并、交與互斥的含義;兩個隨機事件獨立的含義;總體、樣本、樣本量的概念;數據的隨機性;簡單隨機抽樣的含義及其解決問題的過程;樣本與總體的關系;分層隨機抽樣的特點和適用范圍，分層隨機抽樣的必要性.

八理解:古典概型;概率的性質;集中趨勢參數的統計含義;離散程度參數的統計含義;百分位數的統計含義;樣本點、有限樣本空間、隨機事件;樣本點和有限樣本空間的含義;隨機事件與樣本點的關系.

三會:用頻率估計概率;計算樣本均值和樣本方差;計算古典概型中簡單隨機事件的概率.

五掌握:分層隨機抽樣的樣本均值和樣本方差;隨機事件概率的運算法則;抽簽法;隨機數法;各層樣本量比例分配的方法.

重點提升數據分析、數學建模、邏輯推理和數學運算素養.

2 數學思想方法引領下的復習

2.1 數形結合，厘清基本概念

借助樹狀圖、表格或者坐標系等工具進行直觀表達，厘清基本概念和基本問題，有利于分析、解決問題.

例1(北師大版《必修3》)小明家的晚報在下午5:30～6:30之間的任何一個時間隨機地被送到，小明一家人在下午6:00～7:00之間的任何一個時間隨機地開始晚餐，那么晚報在晚餐開始之前被送到的概率是多少?

解析

設晚報被送到的時間為x時，晚餐開始的時間為y時，則

如圖1所示，表示區域是邊長為1的正方形，面積S＝1;事件:“晚報在晚餐之前被送到”即為x≤y，設事件A:“晚報在晚餐之前被送到”，表示區域為陰影部分，面積

圖1

點評

解答本題的關鍵是能通過所給的條件準確作出可行域.在利用幾何概型的概率公式求概率時，幾何“測度”可以是長度、面積、體積、角度等，其中幾何度量為長度、面積、體積時的等可能性主要體現在點落在區域Ω上的任何位置都是等可能的.

2.2 分類討論，凸顯概率模型

例2(2021年全國甲卷理10)將4個1和2個0隨機排成一行，則2個0不相鄰的概率為( ).

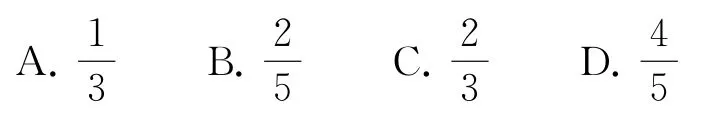
解析

方法1將4個1和2個0隨機排成一行，可利用插空法，4個1產生5個空，若2個0相鄰，有＝5種排法，若2個0不相鄰，有＝10種排法，故2個0不相鄰的概率為故選C.

方法24個1和2個0隨機排成一行，共有種排法.2個0不相鄰，先將4個1全排列，再用插空法將2個0放入，共有＝10種排法，故2個0不相鄰的概率為.故選C.點評

計數原理問題能體現分類討論的思想，隨機事件中樣本點的計算和隨機變量取值下的概率計算也會用到分類討論.

2.3 函數與方程，強化基礎

例3(2017年全國Ⅱ卷理13)一批產品的二等品率為0.02，從這批產品中每次隨機取一件，有放回地抽取100次，X表示抽到的二等品件數，則D(X)＝_________.

解析

由于是有放回的抽樣，所以X服從二項分布，即X～B(100，0.02)，則

點評

本題考查離散型隨機變量方差的求法、二項分布的性質等基礎知識，考查運算求解能力、函數與方程思想，比較基礎.

2.4 化歸轉化，以舊攻新

例4(2017年全國Ⅰ卷文19)為了監控某種零件的一條生產線的生產過程，檢驗員每隔30 min從該生產線上隨機抽取一個零件，并測量其尺寸(單位:cm).表1是檢驗員在一天內依次抽取的16個零件的尺寸.

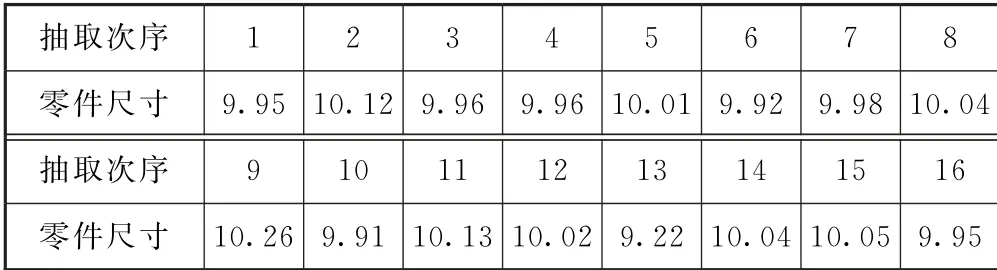
表1

其中xi為抽取的第i個零件的尺寸，i＝1，2，…，16.

(1)求(xi，i)(i＝1，2，…，16)的相關系數r，并回答是否可以認為這一天生產的零件尺寸不隨生產過程的進行而系統地變大或變小(若|r|＜0.25，則可以認為零件的尺寸不隨生產過程的進行而系統地變大或變小).

(ⅰ)從這一天抽檢的結果看，是否需對當天的生產過程進行檢查?

附:樣本(xi，yi)(i＝1，2，…，n)的相關系數

解析

(1)(xi，i)(i＝1，2，…，16)的相關系數為r＝

因為|r|＜0.25，因此可以認為這一天生產的零件尺寸不隨生產過程的進行而系統地變大或變小.

(2)(ⅰ)由于ˉx＝9.97，s≈0.212，由樣本數據可以看出抽取的第13個零件的尺寸在(ˉx－3s，ˉx＋3s)以外，因此需對當天的生產過程進行檢查.

剔除第13個數據，剩下數據的樣本方差為

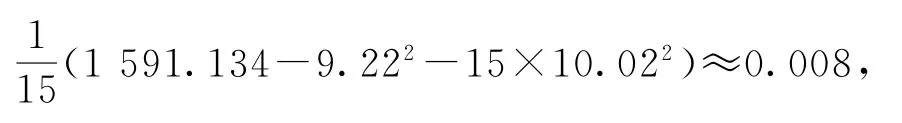
這條生產線當天生產的零件尺寸的標準差的估計值為0.09.

點評

解答創新題時，一要通過轉化，化“新”為“舊”;二要通過深入分析，多方聯想，以“舊”攻“新”;三要創造性地運用數學思想方法，以“新”克“新”，應特別關注創新題型的切入點.

2.5 函數思想，攻堅克難

例5(2021年新高考Ⅱ卷21)一種微生物群體可以經過自身繁殖不斷生存下來，設一個這種微生物為第0代，經過一次繁殖后為第1代，再經過一次繁殖后為第2代……該微生物每代繁殖的個數是相互獨立的且有相同的分布列，設X表示1個微生物個體繁殖下一代的個數，P(X＝i)＝pi(i＝0，1，2，3).

(1)已知p0＝0.4，p1＝0.3，p2＝0.2，p3＝0.1，求E(X);

(2)設p表示該種微生物經過多代繁殖后臨近滅絕的概 率，p是 關 于x的 方 程p0＋p1x＋p2x2＋p3x3＝x的一個最小正實根，求證:當E(X)≤1時，p＝1，當E(X)＞1時，p＜1;

(3)根據你的理解說明(2)問結論的實際含義.

解析

(1)E(X)＝0×0.4＋1×0.3＋2×0.2＋3×0.1＝1.

(2)證法1(函數零點法)

設f(x)＝p0＋p1x＋p2x2＋p3x3－x(x∈[0，1])，則f′(x)＝p1＋2p2x＋3p3x2－1.

當μ＝E(X)≤1時，對于任意的x∈[0，1]都有f′(x)≤f′(1)＝μ－1≤0，則f(x)在[0，1]上單調遞減，又因為f(1)＝p0＋p1＋p2＋p3－1＝0，所以f(x)在[0，1]上有且只有一個零點，故p＝1.

當μ＝E(X)＞1時，對于任意的x∈[0，1]都有f″(x)＝2p2＋6p3x≥2p2≥0，則f′(x)在[0，1]上單調遞增.因為f′(0)＝p1－1＜0，且f′(1)＝μ－1＞0，所以f′(x)在[0，1]上有唯一零點λ∈[0，1)，當x∈[0，λ]時，f′(x)≤0，則f(x)在[0，λ]上單調遞減，當x∈(λ，1]時，f′(x)＞0，則f(x)在[λ，1]上單調遞增，又因為f(0)＝p0≥0，f(λ)＜f(1)＝0，所以f(x)在[0，1)上有且只有一個零點p∈[0，λ]，故p＜1.

綜上所述，當E(X)≤1時，p＝1;當E(X)＞1時，p＜1.

證法2(因 式 分 解 法)p0＋p1x＋p2x2＋p3x3＝x，由p0＋p1＋p2＋p3＝1，得

設f(x)＝p3x2＋(p2＋p3)x－p0，則f(x)的對稱軸又f(0)＝－p0＜0，f(1)＝p1＋2p2＋3p3－1＝E(X)－1，所以當E(X)≤1時，f(1)≤0，故f(x)的正實根大于或等于1，故原方程的最小正實根p＝1;當E(X)＞1時，f(1)＞0，故f(x)的正實根小于1，故原方程的最小正實根p＜1.

(3)意義:每一個該種微生物繁殖后代的平均數不超過1，則若干代必然滅絕，若繁殖后代的平均數超過1，則若干代后被滅絕的概率小于1，該微生物會多代繁殖下去.

點評

表面看這屬于滅絕概率問題，但經過分析發現是三次函數問題，不管是零點分析法，還是因式分解法，都是用函數思想進行研究，應用導數求得其最小值點.

2.6 偶然與必然，呈現問題規律

概率統計研究過程是在偶然中尋找必然，再用必然規律解決偶然問題.主要是收集數據、整理數據和分析數據等處理數據的能力，從數據中提取信息，用信息說明問題、下結論或者分析結論，從而用數據說話.

例6(2021年新高考Ⅰ卷18)某學校組織“一帶一路”知識競賽，有A，B兩類問題.每位參加比賽的同學先在兩類問題中選擇一類并從中隨機抽取一個問題回答，若回答錯誤則該同學比賽結束;若回答正確則從另一類問題中再隨機抽取一個問題回答，無論回答正確與否，該同學比賽結束.A類問題中的每個問題回答正確得20分，否則得0分;B類問題中的每個問題回答正確得80分，否則得0分.

己知小明能正確回答A類問題的概率為0.8，能正確回答B類問題的概率為0.6，且能正確回答問題的概率與回答次序無關.

(1)若小明先回答A類問題，記X為小明的累計得分，求X的分布列;

(2)為使累計得分的期望最大，小明應選擇先回答哪類問題?請說明理由.

解析

(1)由題可知，X的所有可能取值為0，20，100，則

因此，X的分布列如表2所示.

表2

(2)由(1)知，E(X)＝0×0.2＋20×0.32＋100×0.48＝54.4.若小明先回答B類問題，記Y為小明的累計得分，則Y的所有可能取值為0，80，100，有

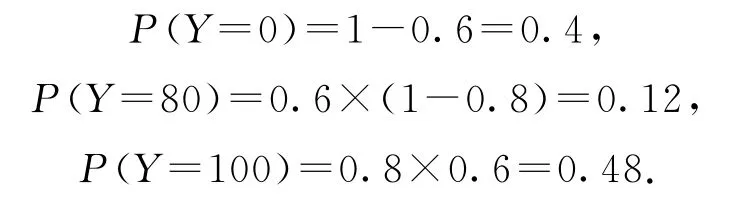
所以E(Y)＝0×0.4＋80×0.12＋100×0.48＝57.6.因為54.4＜57.6，所以小明應選擇先回答B類問題.

點評

通過“分布”與“期望”兩個方面獲取隨機變量的規律，在偶然中尋找必然，在尋找規律的過程中，還要求樣本均值、樣本方差、相關系數等，比如，2021年全國甲卷理科第17題考查了2×2列聯表，要求根據數據求K2，以判斷甲、乙機床的質量差異.