基于MEEMD與相關分析的行星齒輪箱測點優化*

魏秀業 程海吉 賀 妍 史大正 范星宇

(①中北大學機械工程學院，山西 太原 030051; ②先進制造技術山西省重點實驗室，山西 太原 030051;③國能榆次熱電有限公司，山西 晉中 030600; ④黃河萬家寨水利樞紐有限公司，山西 太原 030009)

機械傳動設備的故障問題一直困擾著機械工程的技術人員。在故障診斷過程中，傳感器的數量會極大地增加故障診斷的成本。王子涵等人對局部線性嵌入的行星變速箱測點進行優化[1]，張林等人提出基于模糊聚類與灰色理論的機床主軸溫度測點優化方法[2]。本文以行星齒輪箱為研究對象，提出了一種基于改進的集成經驗模態分解(MEEMD)[3]信息熵與相關分析的行星齒輪箱測點優化方法。

1 MEEMD分解算法

經驗模態分解(EMD)與小波包分解信號等時頻分析方法相比，更能反映信號的物理意義，但無法克服模態混疊現象。EEMD算法即使是對EMD分解得到的IMF分量求均值，以消除隨機白噪聲的影響，但還是會發現噪聲消除不完全，使得部分IMF有失真且信號重構誤差大。因此，本文采用了改進的集成經驗模態分解(MEEMD)方法，有效地消除模態混疊現象，減少了重構誤差。具體分解步驟如下：

(1)將原始信號x(t)，添加2組振幅和標準差相等且方向相反的正負白噪聲mi(t)，得到：

(1)

式中：ai為幅值;Me為白噪聲的對數。

(2)

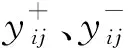
(3)分解信號得到每階IMF分量：

(3)

(4)因為yj(t)存在模態分裂的問題，在此需對yj(t)進行EMD分解，有

(4)

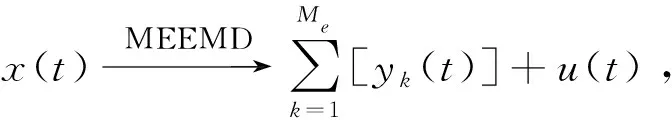
2 信息熵

信息熵是一種反映信息不確定性的指標，計算過程簡單高效。信息的不確定性程度越高，信息熵的值就越大，反之越小。高信息度的信息熵是非常低的,低信息度的信息熵則相當高。信息熵具有單調性，非負性和累加性的性質。本文利用信息熵的特性，使用信息熵作為振動測試信號的特征值。信息熵表示為：

(5)

3 測點的相關性分析[4-6]

相關系數r是研究變量之間線性相關程度的物理量，是反映2個變量之間相關程度的指標，它最早由著名統計學家卡爾·皮爾遜設計。相關系數較為常用的是皮爾遜相關系數。絕對值數值大小在0～1變化。其表達式為：

(6)

若直接對行星齒輪箱振動的原始信號提取特征值進行相關性分析，由于存在強烈的噪聲信號干擾，導致分析出各測點之間的相關性不夠準確。因此，本文提出了一種基于改進的集成經驗模態分解(MEEMD)信息熵與相關分析的行星齒輪箱測點優化方法。基本步驟如下：

(1)信號數據采集:布置試驗臺，人為設置包含單一工況與復合工況的5種工況，采集各工況的振動加速度信號。分別依次對各工況各測點數據進行采集，組成各信號樣本。

(2)特征提取:分別對不同測點的各類工況樣本依次截取時間為0.2 s數據進行MEEMD分解，分解出多個IMF分量。計算各分量與原始數據的相關性。篩選相關性大的P個分量作為有效分量，并進行信息熵計算，將其作為特征向量。構造成特征向量矩陣。

(3)控制同一工況不變，分別對不同測點的特征向量矩陣X和Y進行相關分析。依次將5種工況各測點的相關性進行求解。列表對比篩選出每種工況相關性最低與相關性最高的一組測點。

(4)利用信息熵的累加性原則，控制同一測點不變，對復合工況和復合工況中包含工況的熵值和組成的特征向量矩陣X和Y進行相關性分析。依次對各測點的數據進行求解。列表對比篩選出相關性較低的測點。對各測點的相關性大小進行排序。

(5)優化結論:對于控制同一工況不同測點篩選出的相關性最高的5組測點，對比分析出相對冗雜多余測點。對于相關性最低的5組測點，分析對比出與最優測點相關性較低的測點定義為相對無效測點。控制測點不變，分析復合工況和復合工況包含工況的熵值和進行相關性計算，算出的各測點的相關性大小進行排序。兩類分析方法進行綜合分析，從而達到測點優化的目的。

4 行星齒輪箱測點優化試驗分析[7]

4.1 測點布置

本次試驗使用如圖2所示的試驗臺進行。

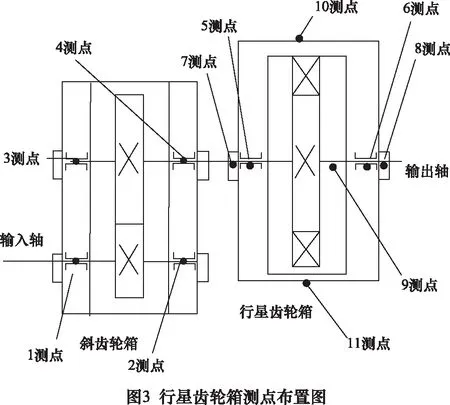
試驗采樣時將電機的轉速調整到1 500 r/min，采樣頻率設置為10.24 kHz。設置負載為0.3 Α。檢查測點信號是否正常。

本次試驗設置5種工況11個測點進行振動信號采集，其中通過人為設置4種故障工況模擬行星齒輪箱微弱故障，5種工況分別為：正常工況、行星輪單齒裂紋、太陽輪軸承外圈裂紋、復合工況一(太陽輪齒面磨損+行星輪2個齒磨損)、復合工況二(太陽輪齒面磨損+行星輪2個齒磨損+行星輪單齒裂紋)，依次定義為工況一～工況五。依次更換齒輪，對5種故障工況的振動信號，依次進行采集。各測點名稱如表1所示。

4.2 選取故障特征值

運用MEEMD信息熵對行星齒輪箱振動信號進行特征提取。對由上節采集到的5種工況下的行星齒輪振動信號分別進行MEEMD分解，截取時間為0.2 s，采樣點數為2 048，分解得到多個IMF分量，其中以正常工況1測點數據MEEMD分解圖為例如圖4與圖5所示。

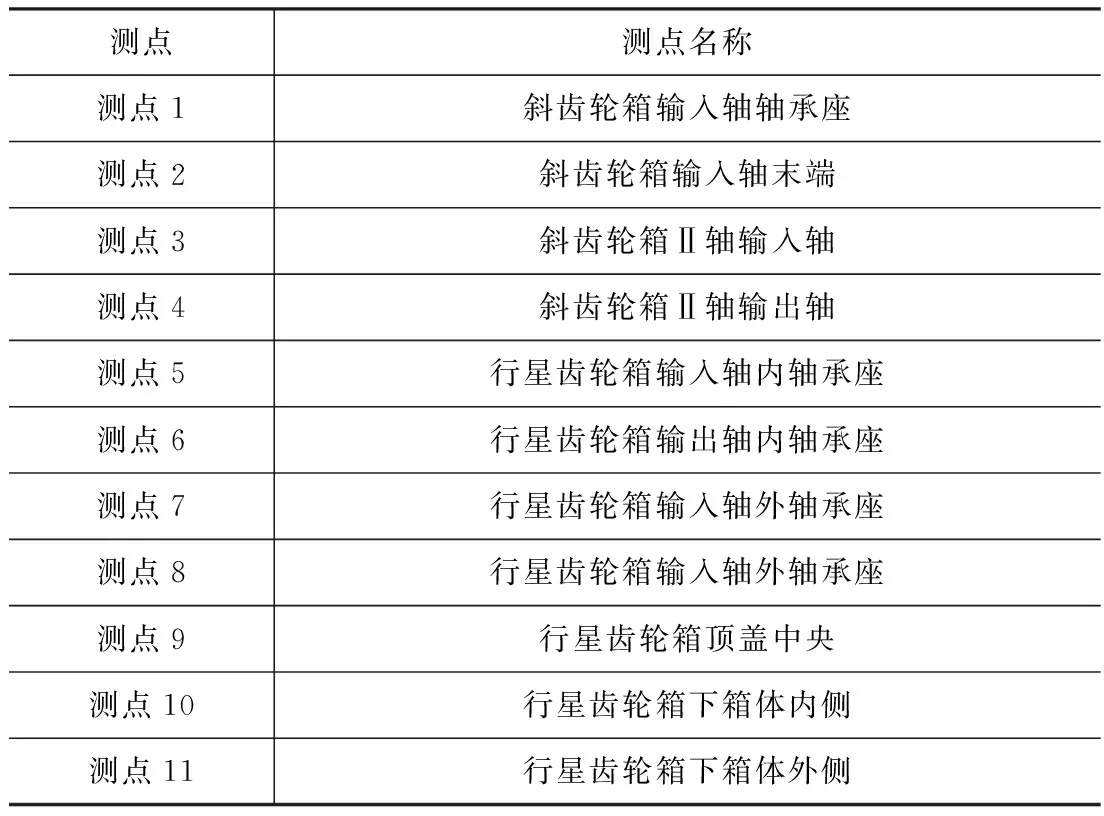
表1 行星齒輪箱測點名稱表

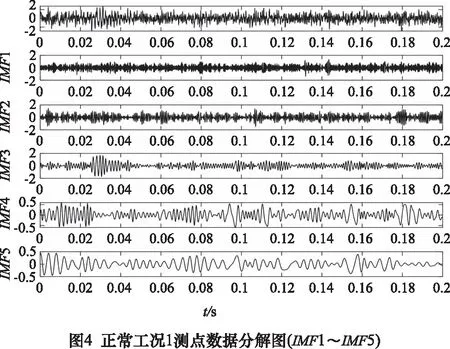
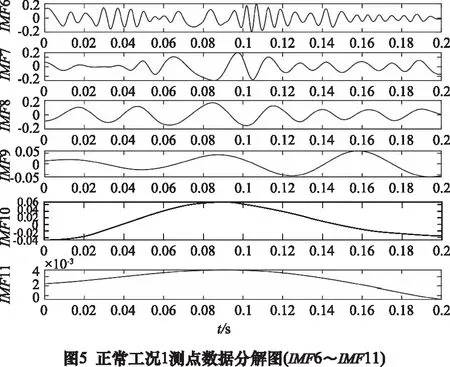
分解得到的IMF分量，采用相關系數進行篩選包含主要故障的分量。原始信號與非真實分量的相關系數較小。以各工況下測點1～測點3原始信號與各IMF分量的相關系數為例如表2所示，通過分析研究各分量與原始信號數據相關系數的大小，發現各工況下原始信號與IMF5以前分量的相關系數均大于0.1，由此認為前5個IMF分量為真實分量。

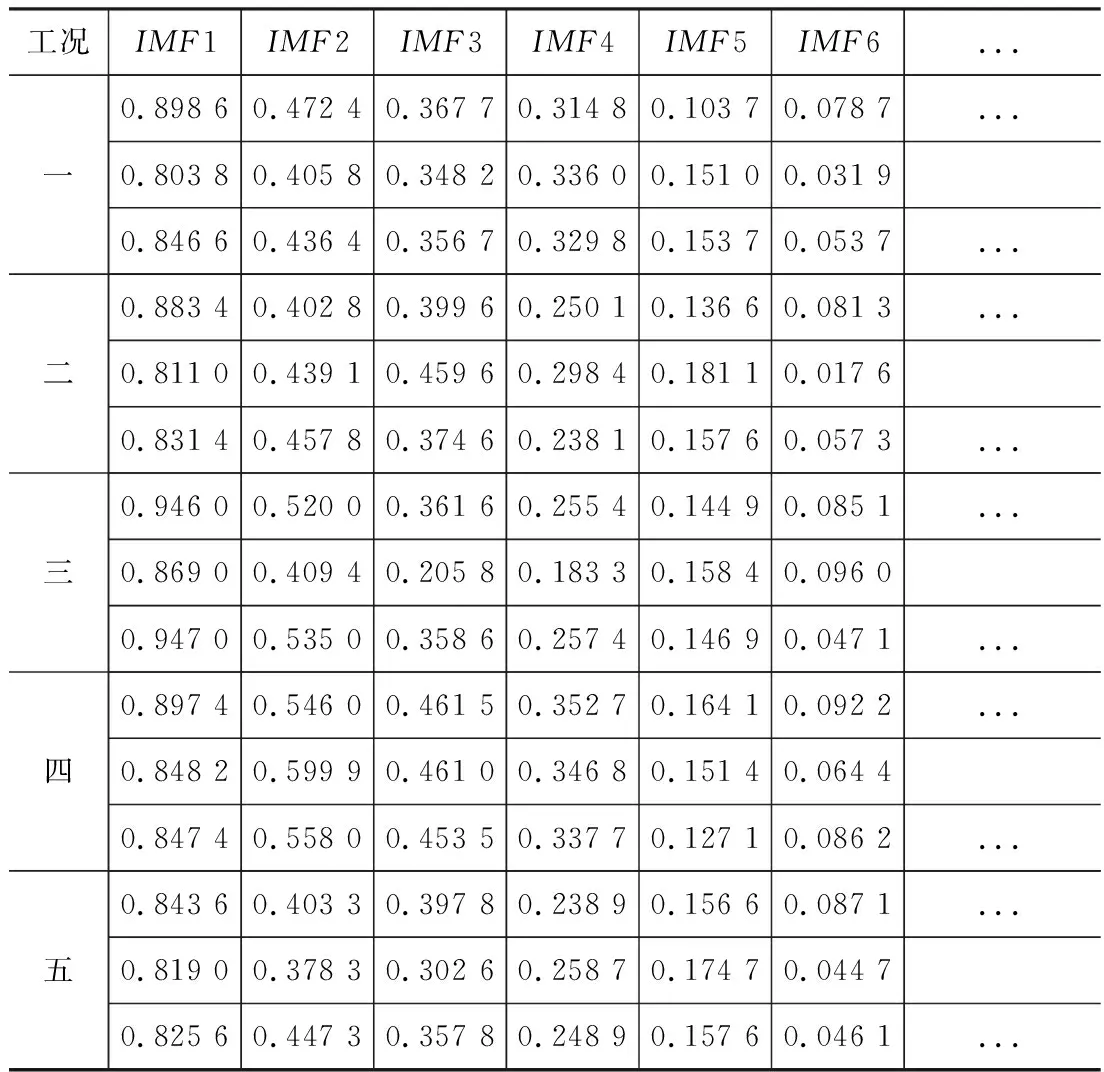
表2 各工況測點1～3相關系數表

對各工況各測點信號MEEMD分解得到的前5個IMF分量進行信息熵的計算，構成特征向量，組成樣本特征矩陣。以工況二(行星輪單齒裂紋)的特征向量矩陣為例如表3所示。

表3 工況二各測點的特征向量

4.3 相關性分析

控制同一工況，對不同測點的特征向量矩陣進行相關性分析。依次對5種不同工況的數據進行計算，篩選出相關性最高和相關性最低的測點組數。以工況三(太陽輪軸承外圈裂紋)不同測點的相關性為例如表4所示。

表4 太陽輪軸承外圈裂紋各測點的相關性

控制同一測點，對復合工況和復合工況所包含的工況的熵值和進行相關性分析。本文復合工況二為：太陽輪齒面磨損+行星輪兩個齒磨損+行星輪單齒裂紋。復合工況一為：太陽輪齒面磨損+行星輪兩個齒磨損。工況二為：行星輪單齒裂紋。依次對各測點復合工況二與復合工況一加工況二的熵值數據進行相關性計算。計算結果如表5所示。

4.4 結果與分析

通過數據結果表明。在控制同一工況，不同測點的相關性分析時。統計數據如圖6所示。研究結果顯示工況一、工況三、工況四均為測點6與測點8的相關性最高。工況二、工況五均為測點5與測點7的相關性最高。所以測點6與測點8優選其一，測點5與測點7優選其一。

研究數據結果顯示工況一、工況四均為測點5與測點10的相關性最低。工況二、工況三均為測點3與測點5的相關性最低。工況五為測點2與測點7相關性最低。若測點5為較優測點，則測點3與測點10為相對較差測點，不然則相反。測點2與測點7亦然。

在控制同一測點，不同工況的相關性分析時。對復合工況和所包含的工況的熵值和進行相關性分析結果統計如圖7所示。

表5 各測點相關性數據統計

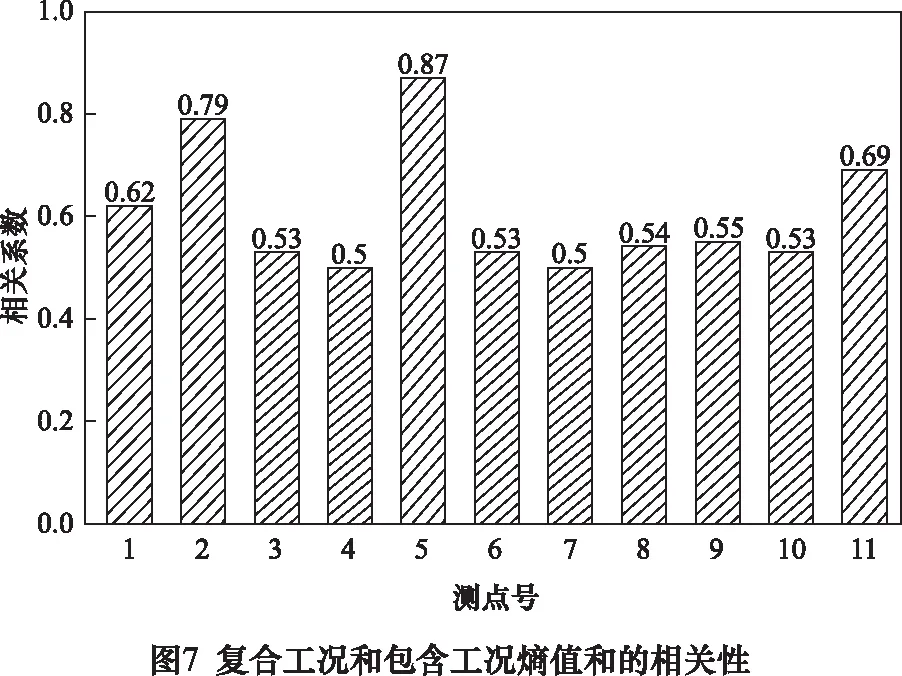
分析數據結果顯示測點5的相關性最大為0.872 7。測點4與測點7的最小，分別為0.502 9和0.500 7。根據統計圖結果可分析。測點6與測點8優選測點8，測點5與測點7優選測點5。測點3與測點10為相對較差測點。

綜上所述，用兩種相關分析法綜合表明，優化剔除的測點為：測點3、測點4、測點6、測點7、測點10。最終保留的優選測點為：測點1、測點2、測點5、測點8、測點9、測點11。

5 結語

分析結果表明，該方法能夠有效優選出最優測點，減少在機械傳動設備行星齒輪箱的故障診斷中傳感器的數量，從而有效地降低了檢測成本。

針對行星齒輪箱振動信號故障診斷中傳感器布置數量的問題，本文提出的一種基于改進的集成經驗模態分解(MEEMD)信息熵與相關分析相結合的行星齒輪箱測點優化方法。對于機械傳動部件行星齒輪箱極易發生故障的問題，本文提到的方法對行星齒輪箱的故障檢測中測點的布置，提供了很好的思路。針對傳感器的冗雜問題有了很好的解決，極大地降低了經濟成本。使得使用少量的傳感器，檢測出真實的故障信息。

本文具體創新點如下：

(1)本文采用MEEMD分解方法，將原始信號自適應地分解出11個IMF分量，將噪聲干擾信號有效的區分，抑制了模態混疊現象。

(2)使用了信息熵疊加性的特性，用信息熵來表達樣本數據的特征值，能夠很好的表達故障特征。

(3)結合相關分析方法，采用控制變量的方法，從數據定量角度進行分析問題。