基于改進蝗蟲優化算法的移動機器人路徑規劃*

徐亞杰 王海星

(①鄭州升達經貿管理學院信息工程學院，河南 鄭州 451191;②河南理工大學電氣工程與自動化學院，河南 焦作 454003)

路徑規劃能力是移動機器人完成自主移動必須具備的能力之一，一直以來都備受國內外學者的青睞，開展了大量的研究工作，許多移動機器人路徑規劃方法相繼被提出并應有。從目前國內外相關文獻來看，這些方法大致可分為傳統方法和智能方法兩類。傳統方法主要包括人工勢場法[1-2]、A*算法[3-4]等，它們的運算速度相對較慢，而智能算法在總體運算效率、路徑規劃效果等方面普遍要比傳統算法更優。因此，基于智能算法的機器人路徑規劃的應用也越來越多。如變步長蟻群算法[5]、自適應遺傳算法[6]、改進人工魚群算法[7]、混合灰狼算法[8]、混合粒子群算法[9]和鯨魚優化算法[10]等多種智能算法都被應用到了機器人的路徑規劃中，并且均得到了較為理想的路徑規劃效果。

2017年提出的蝗蟲優化算法(grasshopper optimization algorithm, GOA)同前文提及的智能算法一樣，也是一種智能優化算法，目前已得到廣泛應用[11-13]。但GOA同前文所述的智能算法相似，算法本身存在有易陷入局部最優、后期收斂精度不足等問題[14-15]，如果直接將其用于機器人的路徑規劃中，算法本身存在的缺陷勢必會對路徑規劃效果造成影響。因此，有必要對其缺陷進行改進設計，以達到提升機器人路徑規劃效果的目的。

本文以GOA為移動機器人路徑規劃方法，同時針對GOA存在的缺陷，對其進行改進設計，提出改進蝗蟲優化算法(improved grasshopper optimization algorithm, IGOA)，以提升機器人路徑規劃效果。機器人2種不同行駛環境的路徑規劃實例驗證了IGOA算法的有效性。

1 柵格法中的蝗蟲優化算法

通過智能算法進行移動機器人的路徑規劃包含兩部分內容，一是進行環境建模，二是通過智能算法反復迭代得到最優路徑。進行環境建模的方法有很多種，如可視圖法、單元分解法、幾何法和柵格法等，其中柵格法最簡單且應用最為廣泛。

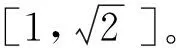
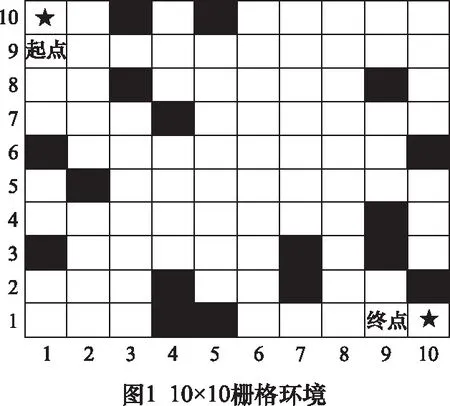
根據柵格法的原理，建立1個如圖1所示的10×10柵格的機器人行駛區域。圖1中，黑色柵格表示障礙物，將其賦值為1，即機器人不能觸碰或翻越該柵格；白色柵格表示可行區域，將其賦值為0，即機器人可在其上自由移動。路徑規劃從左上角的起點至右下角的終點，每步移動的長度在1×1正方形柵格內，最長距離為斜對角。

2 蝗蟲優化算法

眾所周知，GOA是模仿自然界蝗蟲的覓食行為而提出的一種智能仿生算法。在GOA中，蝗蟲個體所在的位置表示所求優化問題的一個候選解，它主要受蝗蟲種群間的相互作用力、風力和重力等3個因素的影響，可用式(1)所示的數學模型進行表示。

Xi=Si+Gi+Ai

(1)

式中:Xi為第i只蝗蟲所處的位置；Si為第i只蝗蟲所受種群間相互作用力的影響；Gi為第i只蝗蟲所受外界重力的影響；Ai為第i只蝗蟲所受外界風力的影響。在進行數學優化問題求解時，為了對數學模型進行優化，式(1)中的外界重力影響Gi和風力影響Ai需要被替換為目標食物的位置Td。這樣，式(1)就可以改寫成式(2)。

Xi=Si+Td

(2)

其中：Si主要通過式(3)計算。

(3)

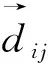
(4)

式(3)中的s函數為計算蝗蟲種群間相互作用力的函數，其表達式如式(5)所示。

(5)

其中：f為吸引強度參數、r為吸引尺度參數。

在整個搜索迭代的過程中，蝗蟲每個位置優劣的評價指標為適應度函數(目標函數)。對于移動機器人路徑規劃而言，適應度函數通常采用得最多的是滿足移動路徑最短。在進行優化問題的求解過程中，式(2)被不斷用來循環迭代以得到最優解，每完成一次迭代后得到的最優適應度值即被記錄為當前得到的最優解，最優解所在位置即被視為目標食物的位置Td，直至達到最大迭代次數。

3 改進蝗蟲優化算法

從蝗蟲優化算法的基本原理可知，在其整個計算過程中，蝗蟲種群幾乎沒有變化，缺乏隨機因素，且沒有跳出局部最優的機制，這就使得算法比較容易陷入局部最優后無法跳出，最終影響優化性能。文獻[14]提出了一種混合變異蝗蟲優化算法(MMGOA)，通過柯西變異對蝗蟲位置進行擾動，從而保證蝗蟲個體具有一定概率跳出局部最優。而柯西分布概率密度函數可知，生成短步長的概率遠高于長步長，這就使得對蝗蟲位置的擾動以小擾動為主，并不能保證蝗蟲真正能夠跳出局部最優；文獻[15]提出了一種多目標蝗蟲優化算法(MOGOA)，通過曲線自適應策略對參數進行調控，從而一定程度上實現了算法前后搜索能力的平衡。而曲線自適應策略的參數值前大后下，雖前期收斂較快，但在后期參數值較小時，容易導致陷入局部最優。

針對上述問題，本文借鑒MMGOA和MOGOA對GOA的改進思路，從兩個方面對GOA進行改進設計，得到IGOA算法。

3.1 Levy飛行局部搜索策略

Levy飛行策略是一種移動步長隨機性極強的行走方式，能夠保證生成長、短步長的概率大體相當(柯西分布短步長的概率遠大于長步長)。將Levy飛行隨機步長引入到GOA算法中，可以增強算法的隨機性和局部搜索能力，提高跳出局部最優的概率。當蝗蟲種群在完成一次迭代搜索后，通過Levy飛行步長對蝗蟲個體所在的位置進行局部調整，如式(6)所示。

X=X+10×sts×L×X

(6)

其中：sts為一個閾值函數，用于控制飛行方法和變化概率，其計算方式如式(7)所示；L為Levy飛行步長，其計算方式如式(8)所示。

sts=sign(xtrans-1)+sign(xtrans+1)

(7)

其中：xtrans為[-3,3]之間的隨機數，sign為符號函數。

L=μ/|v|1/β

(8)

其中：參數β范圍為(0,2)，一般取1.5；參數μ、v服從式(9)所示的正太分布，標準差σμ、σv的取值根據式(10)計算。

(9)

(10)

在一定程度上，Levy飛行的引入為蝗蟲個體提供了一定的“視覺”，能夠讓蝗蟲個體“看清”自身周圍一片區域內食物的情況，使得蝗蟲個體能夠在局部范圍內進行更有針對性的搜索。

3.2 線性遞減參數隨機跳出策略

為保證GOA前后搜索能力的平衡且具有跳出局部最優的機制，提出線性遞減參數的隨機跳出策略(曲線自適應策略雖在一定程上平衡了前后搜索能力，但在后期容易導致陷入局部最優)。當蝗蟲個體搜索到當前最優解的位置后，利用該位置對原位置進行替換，如果沒有搜索到最優解，則啟動隨機跳出策略，其計算方式如式(11)所示。

Xi=(2×(0.5-rand(0,1))+1)×Xi

(11)

其中：Xi是蝗蟲i所在位置。假如搜索到的新Xi更優，則對舊Xi進行替換，替換一次則可認為成功完成了一次跳出行為。為了保證跳出成功后的位置信息能夠被有效利用，將搜索迭代式(2)調整為式(12)：

Xi=Si+(1-p)×Td+p×Xi

(12)

其中：p是控制協調參數，首次迭代時為0。它按照式(13)進行計算。

(13)

根據式(13)可知，當蝗蟲個體未進行跳出或者跳出失敗時，p仍然為0，這就保證了只有Si和Td能夠影響下一次迭代；當蝗蟲個體完成了一次成功跳出后，p在后續的3次迭代中按照0.35的間隔逐步線性遞減為0，這就保證了蝗蟲個體在成功跳出一次局部最優后能夠對后續3次迭代產生影響。

3.3 IGOA算法流程

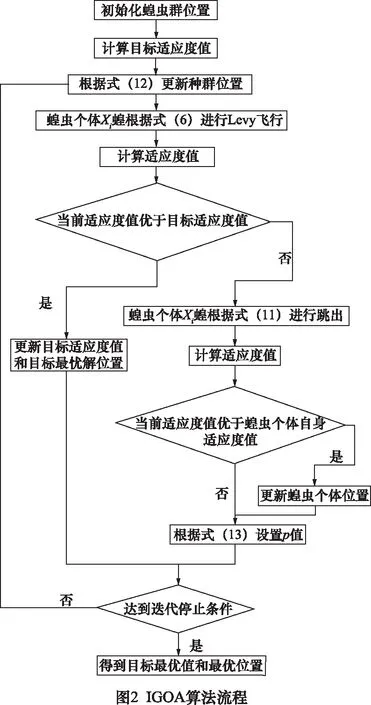
根據GOA算法基本原理和3.1節、3.2節的描述，本文提出的IGOA算法流程如圖2所示。

4 機器人路徑規劃實例分析

本文一共構建了2種機器人行駛環境來對本文所提IGOA方法在路徑規則中的有效性進行驗證。2種環境分別為：在MATLAB中構建的仿真20×20柵格地圖，用于模擬機器人較為簡單的行駛環境；在MATLAB中構建的仿真40×40柵格地圖，用于模擬機器人較為復雜的行駛環境。同時，為驗證本文IGOA的路徑規劃性能，還將其與GOA、參考文獻[14]中的混合變異蝗蟲算法(MMGOA)、參考文獻[15]中多目標蝗蟲算法(MOGOA)進行對比分析。在進行機器人路徑規劃時，上述4種方法中蝗蟲種群的規模均設置為30，迭代達到100次后均停止迭代，輸出最優結果，MMGOA和MOGOA兩種方法的相關其余參數均按原文獻進行設置。

4.1 仿真20×20柵格地圖分析

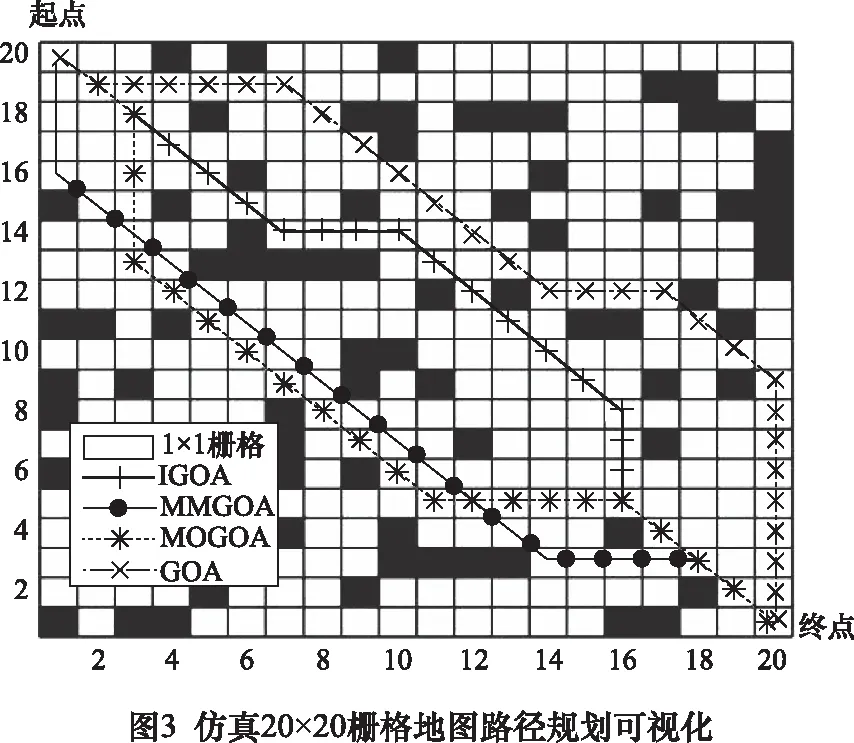
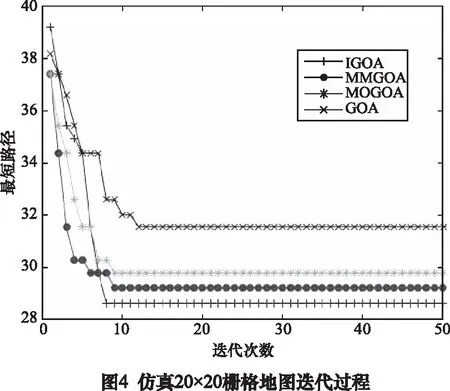
利用4種方法進行仿真20×20柵格地圖中的機器人路徑規劃時，每種方法均獨立運行30次，記錄下每次計算的結果。表1給出了4種方法的計算結果統計，其中平均值為30次計算結果的平均值，耗時為規劃得到最短路徑的時間消耗；圖3給出了4種方法所得最短路徑的可視化結果；圖4給出了4種方法的迭代過程。

由表1、圖3和圖4的結果可知，從最短路徑指標來看，IGOA分別比GOA、MMGOA和MOGOA縮短了9.3%、2%和3.9%；從最長路徑指標來看，IGOA得到結果比其余3種方法的均要好，特別是比GOA得到的最短路徑還要好；從標準差指標來看，IGOA的標準差最小，表明算法的穩定性要好于其余3種；從耗時指標來看，IGOA、MMGOA和MOGOA均是在GOA的基礎上進行的改進，因此算法較GOA的復雜度均有所增加，故耗時不如GOA更優，雖然耗時增加，但得到的路徑均要好于GOA。以上分析結果表明，IGOA在5種評價指標中，除耗時上不如GOA外，其余4種指標均是要優于GOA、MMGOA和MOGOA方法。

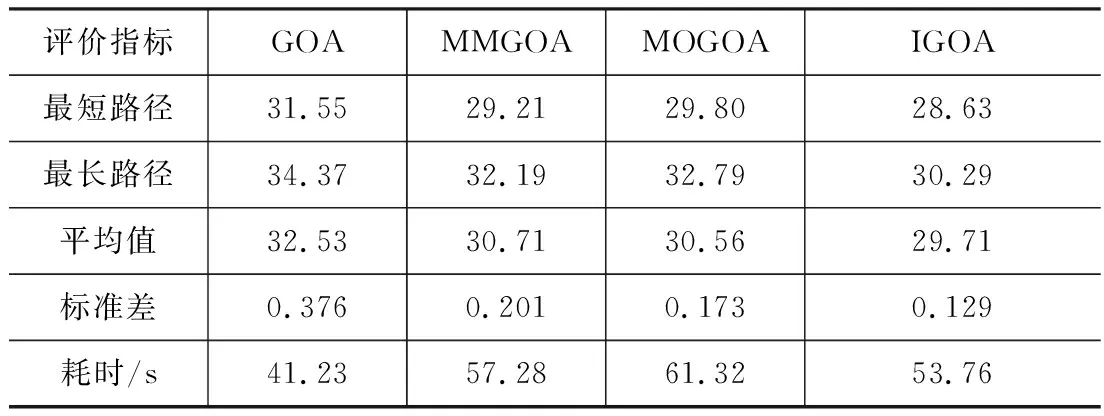
表1 仿真20×20柵格地圖計算結果

4.2 仿真40×40柵格地圖分析

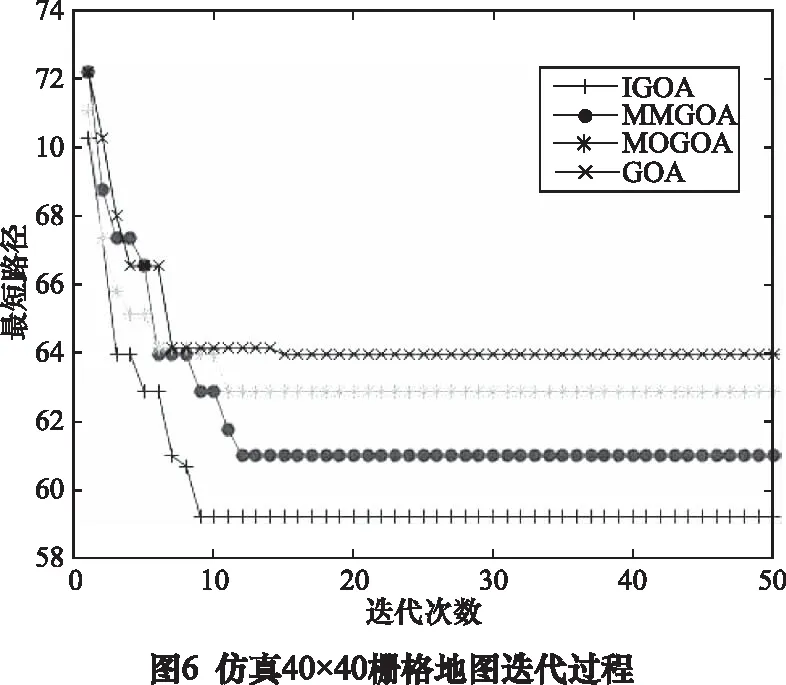
利用4種方法進行仿真40×40柵格地圖中的機器人路徑規劃，分別得到表2的計算結果、圖5的最短路徑可視化結果和圖6的迭代過程。

由表2、圖5和圖6的結果可知，隨著路徑環境的復雜，算法的優勢得以更加明顯的體現。同時也可知，4種方法對仿真40×40柵格地圖的路徑規劃結果和仿真20×20柵格地圖的路徑規劃結果比較相似，即：IGOA在5種評價指標中，除耗時上不如GOA外，其余4種指標均是要優于GOA、MMGOA和MOGOA方法。其中，IGOA的最短路徑指標分別比GOA、MMGOA和MOGOA縮短了7.3%、3%和6.1%； IGOA的最長路徑同樣比GOA得到的最短路徑還要好； IGOA的標準差在0.1以下，而其余3種方法均大于0.1； IGOA的耗時同樣是排名第2。

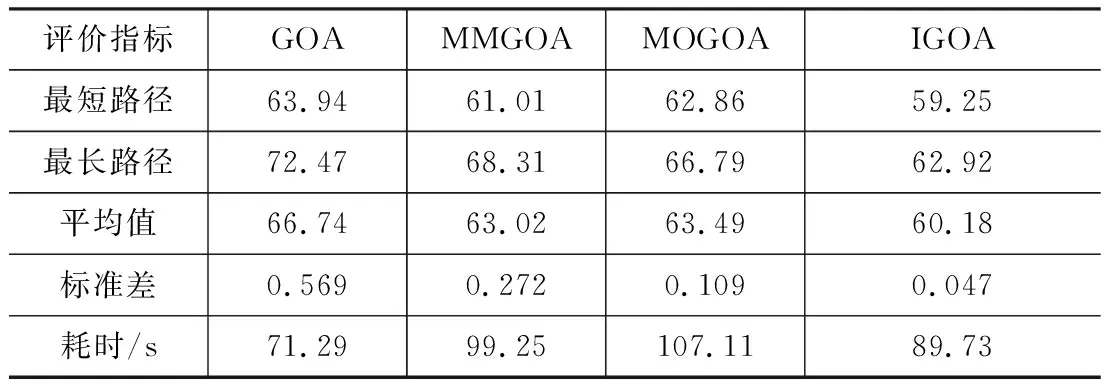
表2 仿真40×40柵格地圖計算結果

5 結語

為有效提升移動機器人的路徑規劃效果，針對GOA存在的不足，將Levy飛行策略局部搜索策略和線性遞減參數隨機跳出策略引入到GOA，提出了IGOA算法。通過移動機器人3種環境下的路徑規劃實例驗證了IGOA算法在路徑規劃中的優勢。