打造“雙減”下的高效復習課堂

王有治

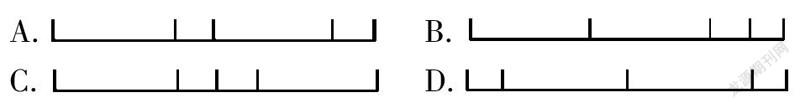
在“雙減”政策下，如何減負不減質，這是更高的要求，更是教育工作者應該思考的問題。復習課對學生學習數學有著鞏固提高的作用，高效高質的復習課，不僅能讓學生較好地掌握所學知識，還能減輕學生的負擔，更是對減負的積極落實。下面筆者結合“圖形與幾何”整理和復習談談自己的看法。

一、以核心知識為線，串聯問題情境

復習課知識面寬、量大，經常出現教師上得“熱火朝天”，學生聽得“昏昏欲睡”。小學六年級數學復習課知識連貫性、綜合性強，如何在一定的時間內完成系統復習，并取得高效高質的復習效果呢？筆者思考：如果能創設多個聯系學生生活實際的教學情境，根據課時內容的需要，以核心知識為主線，將它們串聯起來，對所學的知識進行系統整理，從而使課堂教學成為一個有機的整體，是不是就能打破學生“昏昏欲睡”的現象呢？

在“圖形與幾何”整理和復習中，筆者以周長和面積知識為主線，把農場“籬笆之爭”“土地之爭”“雞圈之爭”三個問題情境串聯起來。

情境一：籬笆之爭。A、B兩個農場主各有一塊農場，他們想把各自的農場圍起來，于是他們共同購買了2000元的籬笆，回來后兩人起了爭執，A說：“我家的土地少，所以我出的錢要少些。”B說：“不對！我們應該出同樣多的錢。”讓學生講講誰說得有理。通過情境的創設，激趣導入，采用說理的方式，引導學生體會圍籬笆與周長有關，體會當圖形的面積不相等，周長有可能相等。

情境二：土地之爭。有兩塊地要分配給兩位農場主（出示兩個形狀不一樣，但面積一樣的圖形），兩個人都搶著要其中一塊地。讓學生幫他們算一算哪塊地大。

采用小組合作的方式，通過計算發現圖形的形狀不一樣，面積都是一樣的，同時提煉出計算組合圖形面積常用的方法，引導學生體驗方法的多樣性，感悟轉化這一重要思想方法。

情境三：雞圈之爭。農場要圍一個雞圈，準備了12.56米的柵欄，讓學生想想怎樣圍，面積是多少？生活中的雞圈是怎么圍的？引導學生全面思考，懂得擇優選擇，學會根據實際情況選擇方案。

學生在一連串問題情境中，激發了回憶知識、解決問題的欲望，學生從“昏昏欲睡”到“躍躍欲試”，提升了教學效果。

二、整合知識網絡，促成自主學習

復習課不同于新授課，不是舊知識的再現、重復，而應該具備知識的整合、能力的培養和智慧的啟迪等功能，從而激發學生自主學習。

如，在“圖形與幾何”整理和復習中梳理溝通相關公式，以及推導過程，形成知識網絡圖，教師留足時間和空間，讓學生進行思考和探索，從而把小學階段所學的有關平面圖形的周長和面積知識進行整理、歸納、類比、同化、內化，引導學生經歷將孤立的、分散的知識整合連成片的過程。

又如，情境三的圍雞圈問題，先讓學生四人小組討論打算怎么圍？學生提出可以圍成長方形、正方形、圓時，教師不給予評價，問：“我們需要分別計算長方形，正方形，圓的面積來區別哪個更大嗎？”從而復習了“周長相等，圓的面積最大”的結論。再問：“還能不能使圍成的雞圈面積更大？”引導學生與生活實際相聯系，可以利用一面墻圍成一個半圓形，還可以利用兩面墻圍成一個四分之一圓，想象、比畫一下是什么形狀的，并引導學生說出不管怎么圍，12.56米都只是周長，要求的是面積。通過計算，提出合理建議，體驗用數據說話的魅力。針對性、思考性、綜合性地運用圓的面積知識解決實際問題。這道題“牽一發而動全身”，既考查了“周長相等圓的面積最大”的知識，又鞏固了圓面積、半圓形面積、四分之一圓面積的計算方法，通過合作探究將這個知識點，拓展到聯系生活實際解決生活問題，滲透根據實際情況選擇最優方案。達到做一題、學一法、通一類、會一片的目標。

三、精心創編練習，提升練習功效

練習作為復習課的重要環節，如何做到“精”“深”“到位”呢？筆者認為要精心設計、挑選有層次性的練習，讓復習課更具新鮮感。復習課上要關注全體學生，激活學生的興奮點，需要補充一些有針對性的練習，讓不同的學生從復習課上得到不同的發展。但更重要的還是要用好、用足書上的練習，讓其發揮最大的功效。在“圖形與幾何”整理和復習一課上的練習除了基礎題（完成書上習題），筆者還設計改編了以下練習。

1.針對性練習。針對教學的重、難點，學生理解困難，容易出錯等方面進行設計。

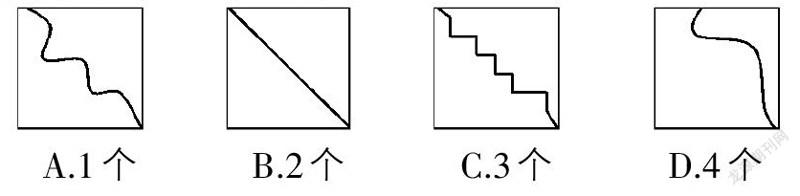
如，復習平面圖形的周長后設計問題：下面四個正方形都被分成了兩個部分，分割后兩部分周長相等的圖形有（）個。

A.1個 B.2個 C.3個 D.4個

又如，補充針對圖形的特征進行練習：有4條鐵絲，按記號折一折，能圍成一個長方形的是（ ）。

學生通過比較、討論，對平面圖形的周長有更深刻的理解，從而達到知識的合理運用。

2.綜合性練習。考查學生知識間的溝通與聯系，以及將知識點靈活組合的能力。

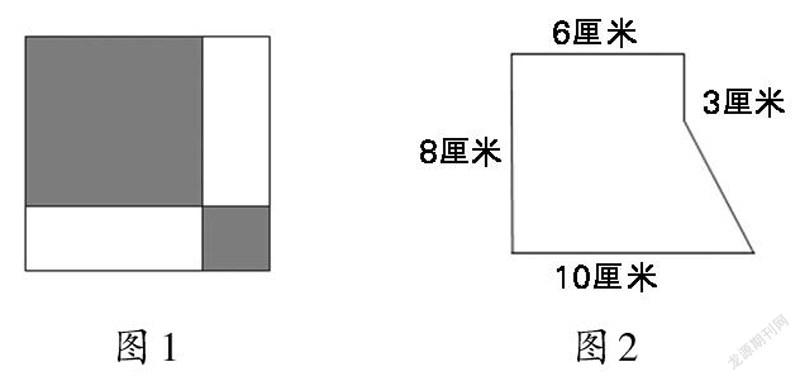
如，下圖（圖1）是個大正方形，已知兩個小正方形（陰影部分）的周長和是48分米，大正方形的面積是（ ）。

A. 24平方分米B. 48平方分米

C. 96平方分米D. 144平方分米

這樣的題目，讓學生體會到正方形周長和面積之間的緊密聯系，通過周長求出邊長，再求出面積，從而引導學生形成正確的思維方式，提高學生的數學能力。

又如，設計說理題（圖2）。

（1）你能看懂這種方法并在圖中標出虛線嗎？

6×3+（6+10）×5÷2

（2）明明同學這樣算，對嗎？說說理由：（6+10）×8÷2-3×4÷2

這種綜合性的題目，讓學生不僅會做，更會說道理，從而靈活、多樣地解決問題。同時，也綜合運用了平面圖形的面積計算方法，數學思維能力得到了提升。在夯實知識的基礎上，數學課堂也成了學生講理的地方。

總之，“雙減”政策下，高效高質的復習課，不僅能讓學生較好地掌握所學知識，還能減輕學生的負擔，更是對減負的積極落實。讓學生在復習課中不斷提高數學知識的應用能力，數學思維品質也得到更好地培養；讓每位教師減負不減質，潛心鉆研、精心組織，把每一節復習課上得余韻悠長，回味無窮。

（作者單位：福建省廈門市集美區后溪中心小學）