三維魚體參數化建模

胡海濤，趙銀君，石敏*，趙國亮，朱登明

（1.華北電力大學控制與計算機工程學院，北京 102206；2.中國科學院計算技術研究所前瞻研究實驗室，北京 100190）

魚類作為水產養殖中最重要的生物物種，對其進行監測有助于提高漁業的精細化管理水平。三維魚體作為重要的量化指標，對預測魚類生長狀況［1］、估 計 魚 群 密 度［2］、分 析 魚類 種 群 結 構［3］具 有 重 要意義。

近年來，隨著三維重建技術的發展，重建范圍不斷擴大，使得水下三維建模成為可能。水下三維建模主要分為主動式重建和被動式重建。主動式重建，通過發射激光雷達［4］、結構光［5］等重建水底環境；被動式重建，通過拍攝水底多視角圖像重建水底環境［6］。但這兩種方法都無法實現對游動魚類的三維重建。在空中雖可利用三維掃描儀［7］、基于雙目視覺的三維重建［8］等方法獲取魚類三維模型，但耗時費力，成本高，得到的三維模型精度不高，且不能快速批量采集，無法對基于三維魚體數據驅動的自動化研究工作提供大量數據。

基于真實三維注冊數據的三維參數化建模已應用于多個領域，主要有人體參數化建模［9-12］、基于真實的人體掃描注冊數據、統計分析人體體型分布空間、構建人體體型參數化表示模型、通過控制相關權參數生成豐富的三維人體模型等。

目前尚未見三維魚體的參數化表示模型，為此，本文提出了一種三維魚體參數化建模方法。主要貢獻有：掃描儀采集真實三維魚體數據，對其進行網格注冊，構建拓撲結構一致的三維魚體數據集，在此基礎上，基于主成分分析法研究三維魚體參數化建模方法，構建三維魚體參數化表示模型，進而快速生成大量三維魚體模型，解決了三維魚體數據獲取困難的問題。

1 相關工作

1.1 三維數據注冊

對三維數據注冊的研究已有多年，其本質是對標準網格模板進行平移、旋轉、變形等操作，使得標準模板能表征所掃描的目標模型。其可分為剛性注冊及在此基礎上的非剛性注冊，剛性注冊只是將標準模板進行平移和旋轉操作，非剛性注冊還會使模板網格發生變形。BESL等［13］提出的最近迭代點（iterative closest point，ICP）算法，通過貪心算法迭代求解2個點云模型之間的對應點，然后用最小二乘法求解得到兩模型之間的旋轉、平移參數，實現2個點 云模型的剛性注 冊。ALLEN等［9］提 出的變形標準模板網格使其逼近真實掃描數據的方法，通過構建拓撲結構一致的網格數據集，實現非剛性注冊。AMBERG等［14］在ALLEN等［9］工作的基礎上提出了非剛性最近迭代點（non-rigid ICP，NRICP）算法，通過迭代尋找最近點實現非剛性注冊，得到了較好的注冊效果。LI等［15］和YAO等［16］提出的非剛性注冊方法均用于解決最小化NRICP中的注冊代價函數，前者通過重加權提高變換矩陣的稀疏性，降低計算量，后者則用優化-最小化（majorization-minimization，MM）算法將每次迭代簡化為L-BFGS的最小二乘問題，2種方法在注冊精度和計算速度上均有所提升。

1.2 參數化建模

三維魚類參數化建模方法多種多樣.涂曉媛等［17］最早提出“人工魚”模型，用生物力學方法建模人工魚的物理和生理結構，設計了“質點-彈簧-阻尼”魚體模型，其主要由23個“質點”和91個“彈簧-阻尼”單元組成。此外，還有三維仿生機器魚模型［18-20］，將魚體作為剛性多級連桿進行建模，但上述方法均不是對真實三維魚體的建模，構建的三維魚體模型主要用于水下環境作業、軍事偵察、考古等，無法用于對魚體體型的研究。

目前尚未發現有基于真實魚體掃描數據進行參數化建模的研究工作。但在人體建模領域，基于真實的三維人體注冊數據集，ALLEN等［9］采用主成分分析法進行了人體體型參數化建模，通過調整身高、體重等參數生成相應的三維人體模型。之后出現了許多用相同方法進行人體體型參數化建模的工作，如 經 典 的 人 體 參 數 化SCAPE模 型［10］、SMPL模型［11］。SCAPE模型在參數化人體姿勢的基礎上也對人體體型進行了參數化，但無法直接通過修改參數生成相應的體型，參數化控制不直接；德國馬普所的SMPL模型提煉了人體的10個體型參數和72個姿態參數，實現了給定參數即可生成對應的人體，但由于對參數缺乏約束，有時會生成不自然的人體，為此，2020年，馬普所提出了STAR模型［12］，在改進上述問題的同時也減少了參數量，是一個輕量級的人體參數化表示模型。

本文的三維魚體參數化方法是受ALLEN等［9］的工作和SMPL模型［11］的啟發，通過控制相關參數，直接快速生成豐富的三維魚體模型。

2 本文方法

提出了一種基于主成分分析的魚體參數化建模方法，主要包括魚體掃描數據注冊和魚體體型參數化建模兩部分，如圖1所示。

圖1 三維魚體參數化建模方法Fig.1 Parametric modeling method of 3D fish body

2.1 魚體標準模板構建

掃描儀采集的原始三維魚體數據，網格頂點數量龐大，拓撲結構雜亂，無法批量放入計算機進行統計分析和參數化建模，需對其進行網格拓撲同構處理，使網格模型具有相同的頂點數以及點之間相同的連接結構。通過標準模板變形，令變形后的模板能表征原始掃描數據，實現對原始掃描數據的注冊，得到拓撲結構一致的三維魚體注冊數據。

采集魚體多視角圖像，由專業建模師在三維建模軟件3ds Max中進行三維魚體標準網格模板建模，見圖2。

圖2 三維魚體標準模板構建Fig.2 Standard template construction of 3D fish body

上述標準魚體模板定義為S=(H，Ε)，其中，H為由m個頂點構成的頂點集，Ε為由n條邊構成的邊集。

2.2 魚體網格注冊

用標準模板對原始掃描數據進行注冊，以原始掃描魚體數據為約束變形標準魚體模板，令其逼近原始掃描魚體，使變形后的模板能表征原始掃描數據。由于所有原始掃描數據的注冊均基于同一標準魚體模板，因此注冊得到的數據具有一致的拓撲結構。本文采用剛性注冊和非剛性注冊相結合的魚體網格注冊方法，用剛性注冊算法為非剛性注冊算法提供初始條件。

2.2.1 剛性注冊

網格注冊時對標準模板和原始掃描數據的初始值較敏感，為此設計了魚體剛性注冊算法，以變換兩者之間的初始位置和大小。以采集的原始三維魚體為坐標原點，因它們處于不同的坐標系，需將掃描數據變換到標準模板坐標系下，使掃描數據和模板的位置盡量重合；因采集的不同生長周期的魚體體型差異明顯，需縮放標準模板，令每個三維魚體的掃描數據均與一個大小相仿的模板模型對應。因此，魚體剛性注冊包含坐標變換和縮放變換。

通過坐標變換將掃描模型變換至模板空間下，目標函數定義為

其中，Told為原始掃描模型，R和t分別為掃描數據坐標系和模板坐標系之間的旋轉和平移參數，Tnew為變換到模板坐標空間的掃描模型。

縮放變換是將模板模型剛性地縮放至接近掃描模型，目標函數定義為

其中，Sold為標準模板，s為模板和掃描數據之間的縮放矩陣，Snew為縮放后的模板。

在剛性注冊時，先進行一次坐標變換，將掃描數據變換至模板坐標系下，再進行縮放變換，將模板縮放至掃描模型大小，縮放變換將導致模板空間位置變動，因此需再進行一次坐標變換，將掃描模型調整至模板坐標系下。剛性注冊算法步驟如下：

輸入掃描網格Told，標準模板Sold。

輸出坐標變換后的網格Tnew，縮放變換后模板的Snew。

Step1第1次坐標變換。

Step1.1求解Told和Sold2個坐標系之間的R和t。

Step1.2用式（1）將Told變換為T1new。

Step2縮放變換。

Step2.1求解T1new和Sold之間的縮放矩陣s。

Step2.2用式（2）將Sold變換為Snew。

Step3第2次坐標變換。

Step3.1求解T1new和Snew2個坐標系之間的R和t。

Step3.2用式（1）將T1new變換為Tnew。

2.2.2 非剛性注冊

通過魚體剛性注冊，在空間位置和大小上令標準模板和掃描模型近似對齊，但作為柔性物體的魚類，魚體之間存在差異，因此，還需進行魚體非剛性注冊，通過調整模板使其逼近掃描模型，令調整后的模板能最大限度地表征掃描魚體模型體型。

用非剛性ICP算法進行魚體模型非剛性注冊，非剛性注冊算法思想如圖3所示，其中，S表示標準模板，S′表示變形后的模板，T表示掃描模型。非剛性ICP算法，即最小化S′和T之間的距離，使S′能夠表征T。

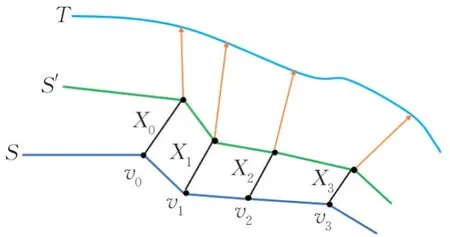
圖3 非剛性ICP算法思想Fig.3 Non-rigid ICP algorithm idea

非剛性ICP算法的目標函數由數據項誤差Ed、平滑項誤差Es和特征點誤差El組成：

其中，X為模板頂點的變換矩陣，α和β分別為Es和El的影響因子。

數據項誤差Ed表征變形后的模板魚體模型與掃描魚體三維網格模型之間網格頂點的接近程度，具體表示為

其中，vi表示模板模型上的第i個頂點，Xi表示對第i個頂點進行的變換，ui表示vi在掃描模型上對應的第i個頂點，wi表示vi頂點的變換對整體的影響權重。式（4）第2個等式為數據項誤差在所有模型數據中的表示。

平滑項誤差Es約束變形過程中相鄰頂點的仿射變換矩陣，令模板平滑形變，具體表示為

其中，ε為模板S中所有邊的集合，G為權重矩陣，M表征點之間的連接關系，M的行表示三角形的邊，列數表示頂點，當第r條邊連接第i個頂點和第j個頂點（i＜j）時，Mri的元素為－1，同時Mrj中的元素為1，其他元素為0，符號?表示求解M和G之間的Kronecker積，下標F表示范數。

特征點誤差El表征變形后模板與掃描模型上對應特征點之間的距離，相當于稀疏的數據誤差項，具體表示為

其中，L={(v1，l1)，(v2，l2)，…，(vi，li)}為特征點。

綜上，目標函數完整的二次損失函數可表示為

令該二次損失函數的導數為0，直接求解，當X=(ATA)-1ATB時，損失函數值最小。

由于特征點需要手動標記，而采集的魚體掃描數據和模板數據頂點數量又較多，只有標記了大量標記點的數據才有較好的注冊效果，但手動標記大量頂點造成的誤差將影響魚體模板模型變形的準確性。基于準確性和配準效率考慮，因在魚體非剛性注冊時沒有使用特征點誤差El，故設置β=0，則在魚體非剛性注冊中，目標函數可簡化為

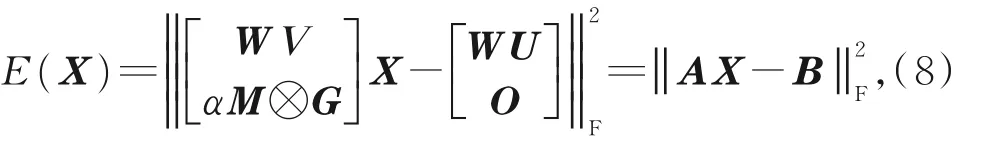
在每輪迭代中，α依次取50，20，2，0.8，0.5，0.35，0.2。

2.3 魚體參數化建模

參數化建模又稱變量建模，通過統計分析三維注冊數據集，用少量變量表征數據集中模型的三維空間分布，由控制變量生成豐富的三維模型。主成分分析（principal component analysis，PCA）作為一種最廣泛使用的數據降維算法，其主要思想是將n維特征映射至k維，稱此k維全新的正交特征為主成分。k維主成分保留了原n維數據中絕大部分維度特征，實現以少數維度表示高維空間。本文用PCA法進行魚體三維模型參數化建模，實現用低維度參數空間表示高維的三維魚體網格數據。

魚體體型空間的PCA參數化可表示為

其中，SE∈R3N表示三維魚體的平均體型，D∈R3N×k表示由k個主成分分量構成的主成分矩陣，S∈R3N表示參數控制生成的具有N個頂點的三維魚體網格模型，ωs∈Rk表示k個可調控參數。

各參數的具體求解過程如下：

魚體模型的體型均值向量SE∈R3N：

其中，K為三維魚體數據集中的魚體網格模型數，Si為第i個魚體的三維網格向量。

對所有魚體數據去均值，得到三維魚體體型的變化空間U：

其中，Ui∈R3N為數據集中第i個魚體去均值后的向量表示，U∈R3N×K為由數據集中所有K個魚體去均值后向量Ui構成的高維矩陣。

分解U求解其特征向量，取前k個特征向量作為主成分，此k維主成分能表征U空間的主要特征：

用一組權參數ws={w1，w2，…，wk}表示魚體模型S：

通過設置權參數ws可合成新的魚體模型，ws即為參數化構造得到的可控制的權參數。

3 實驗與分析

草魚是典型的紡錘魚型，因其體型特征變化明顯，故選擇草魚作為實驗魚。采集草魚的多視角圖像，由專業建模師給出有粒度劃分的拓撲結構清晰的三維魚體標準模板，該標準模板共有9 846個頂點，19 688個三角面片，如圖4所示。

圖4 標準魚體模板Fig.4 Standard fish template

搭建掃描平臺采集草魚的全包圍數據，將草魚掛起，固定魚鰭使其呈張開狀態，用手持式激光掃描儀掃描，如圖5所示。共采集11條處于不同生長期的草魚掃描數據，每個三維魚體掃描數據的三角面片數均超30萬，其中含大量冗余數據。為提高注冊效率，用經典的網格簡化算法：二次誤差量（quadric error metrics，QEM）［21］法簡化原始掃描數據，將三維魚體掃描數據降采樣至近似標準魚體模板的頂點數和三角面片數。

圖5 草魚掃描數據采集Fig.5 Grass carp scan data collection

3.1 魚類剛性注冊實驗

對降采樣后的11條草魚的掃描數據進行剛性注冊實驗。經坐標變換，將草魚的掃描數據變換至標準模板坐標空間；對標準模板進行縮放變換，使采集的所有草魚數據均對應一個大小相近的模板。

圖6給出了4組草魚體剛性注冊的實驗結果。其中，第1行為剛性注冊前的模板模型（淺色）和掃描模型（深色），分別位于2個坐標空間，且大小差異明顯；第2行和第3行為剛性注冊后的效果，模板和掃描模型已調整至同一坐標空間，標準模板調整至近似掃描模型大小。

圖6 剛性注冊實驗結果Fig.6 Results of rigid registration experiment

3.2 魚類非剛性注冊實驗

基于剛性注冊結果進行非剛性注冊實驗，計算機配置為Quad-Core Intel Core i5 CPU@2.00 GHz，內存為16 GB，操作系統為macOS。圖7給出了4組魚體非剛性注冊的實驗結果。以上述剛性注冊結果作為非剛性注冊的輸入，得到的變形模板模型（淺色）高度逼近掃描模型（深色）。

圖7 非剛性注冊實驗結果Fig.7 Results of non-rigid registration experiment

進一步，對變形模板的變形精度進行定量分析，表1記錄了11條草魚掃描數據非剛性注冊后變形模板與掃描數據之間的均方根誤差以及注冊所需配準時間，平均均方根誤差為0.691 3 mm，平均配準時間為45.61 s，注冊精度和配準時間均在可接受范圍，定量分析表明，變形后的魚體模板能很好地表征真實掃描魚體體型。

表1 魚體非剛性注冊均方根誤差及配準時間Table 1 Root mean square error of fish body non-rigid registration and registration time

由于標準魚體模板有9 846個頂點、19 688個三角面片，在最終構建的三維魚類注冊數據庫中，11個魚體模型的頂點數均為9 846，三角面片數均為19 688。

3.3 魚體體型參數化實驗

對上述非剛性注冊構建的三維魚體拓撲數據集進行了魚體參數化建模實驗，圖8為生成的三維魚體平均體型。經多次實驗發現，當k=4，權參數ws={w1，w2，w3，w4}施加在平均魚體體型上時，魚體體型會發生較大變化，而當k＞5時，改變權參數，魚體體型變化不明顯，故取k=4，即采用4維主成分進行定性與定量分析，平均魚體體型默認的權參數為ws={1.000，1.000，1.000，1.000}。

圖8 三維魚體平均體型Fig.8 Three-dimensional mean body shape of fish

圖9給出了魚體定量分析示意，綠線為魚體體長，紅線為體高，藍線為體寬，通過計算體長、體高和體寬，定量分析魚體模型的變化。

圖9 魚體定量分析示意Fig.9 Schematic diagram of quantitative analysis of fish

圖10為改變權參數w1時生成的三維魚體模型的側視圖和俯視圖，第1列為w1=0.851時生成的魚體體型，第2列為w1=1.000時生成的魚體體型，第3列為w1=1.135時生成的魚體體型，可以發現，減小或增大w1，生成的魚體體型較標準魚體體型有所縮小或放大。表2定量分析了權參數w1對魚體體長、體高和體寬變化的影響，發現隨著w1的變化，魚體的體長、體高和體寬均發生了明顯變化，w1控制魚體體型的整體變化。

表2 權參數w1對魚體體型的影響Table 2 The effect of weight parameters w1 on fish body shape

圖10 三維魚體模型隨權參數w1的變化Fig.10 The three-dimensional fish model changes with the weight parameter w1

表3定量分析了通過控制w2，w3，w4中的某一參數，魚體體長、體高和體寬發生的變化。分析發現，隨著其中任一權參數的變化，魚體的體長、體高、體寬只在小范圍內變動。因此，w2，w3，w4對魚體體型只有微調作用。

表3 權參數w2，w3，w4對魚體體型的影響Table 3 The effect of the weight parameters w2，w3，w4 on fish body shape

基于拓撲結構一致的三維魚體數據集構建了三維魚體參數化表示模型，通過改變不同的權參數可快速生成不同體型的三維魚體模型。權參數ws={w1，w2，w3，w4}中，第一主成分對應的權參數w1對魚體體型的控制作用明顯，通過調節w1，生成不同體型的魚體模型；改變權參數w2，w3和w4，魚體體型變化不明顯，此3主成分對魚體模型只起微調作用，表征的是數據集中魚體的個體差異。此外，任一權參數ws不能單獨改變魚體某一維度。分析產生上述2種情況的原因，主要在于數據集規模小，注冊數據集中僅有11條三維魚體模型，而主成分分析法只有在數據集規模為參數量的5～10倍甚至更多時才能實現單維度控制以及令三維模型發生較大變化，因此在數據量較少時，只有權參數w1在生成魚體三維模型時起決定性作用。

4 結論

由于水底環境復雜，三維魚體模型獲取較困難，本文基于主成分分析法對三維魚體參數化建模方法進行了研究，構建了三維魚體參數化表示模型，通過改變相應的權參數，可快速、方便地生成豐富的三維魚體模型，從而解決了三維魚體模型獲取困難的問題。得到的三維魚體模型可應用于魚體三維模型重建、三維動畫等領域，但仍存在以下不足：

（1）由于魚鰭非常輕薄且透明，導致魚鰭掃描不完整。在魚體階段，因魚鰭注冊效果不佳，出現魚鰭三角面片法向量朝內以及三角面片交叉的情況，有待后續重點研究。

（2）在參數化建模階段，由于注冊數據集規模較小，無法做到權參數單維度控制，造成參數設置不直觀，沒有與魚體體型特征的語義相關聯。后續可適當增加三維魚體數據的采集量，將擬合的魚體體型語義參數線性映射至參數化魚體模型權參數空間，實現用具有語義信息的參數，如魚體的體重、體長等生成相應大小的三維魚體模型。