基于動態模態分解的長江口海表溫度時空分布特征重構研究

陳嘉星，江迪，張霄宇，3，4*

（1.浙江大學地球科學學院，浙江 杭州 310027；2.浙江大學信息與電子工程學院，浙江 杭州 310027；3.浙江大學海南研究院，海南 三亞 572000；4.浙江大學海洋研究院，浙江 舟山 316000）

海洋表面溫度（sea surface temperature，SST）是海洋-大氣系統物質和能量交換過程的重要參數之一，是海水熱量傳遞的直接表現形式，SST的變化可影響海洋-大氣系統之間的熱量交換，進而影響區域氣候［1-2］。

長江口海域陸地、海洋、大氣及人類活動等過程的相互作用強烈，水動力過程復雜，長江口海洋表面溫度的分布特征與變化趨勢影響并指示海水運動，是該海域海洋復雜內在動力機制的綜合表現。此外，SST與表層葉綠素a濃度分布、海洋養殖、海洋生物的分布等密切相關［3］。研究長江口海洋表面溫度的時空演變規律對于理解時空耦合系統的深層動力機制、淺海環流及物質輸運等過程極為重要。

關于長江口海洋表面溫度的時空分布特征，前人已有不少研究。周曉英等［4］利用功率譜分析、MK突變檢驗分析了水文站的月均海溫數據和徑流量數據，研究發現長江口海溫的最高值出現在8月，最低值出現在2月，季風和長江徑流對其有顯著影響。孫凡等［5］基于1982—2016年的OISST數據及其他氣象數據，采用回歸分析和滯后相關系數法進行了研究，結果表明，長江口海域海表溫度的長期升溫趨勢主要受該區域徑向熱輸送及長江平流熱輸送增強的影響。買佳陽等［6］基于2000—2012年的中等分辨率成像光譜儀（moderate-resolution imaging spectroradiometer，MODIS-Terra）LIB數 據，通 過優化劈窗算法，建立了適合長江口水域的海表溫度反演模型，并進行了海表溫度反演，分析發現，長江口海表溫度主要受太陽輻射影響，且口內口外的海表溫度具有不同的季節性差異。何全軍等［7］基于2015—2017年我國周邊海域的衛星數據和現場數據，采用多元回歸模型，開發了適用于FY-3C/VIRR數據的區域SST反演算法。AI等［8］利用渤海地區的晴天紅外遙感數據和浮標實測數據，構建了一種適用于渤海地區的SST神經網絡反演模型，并將反演結果與MODIS的SST產品進行了精度評估，結果表明，深度學習可應用于SST反演。以上研究或偏向于水文資料分析，受水文站分布限制，分析僅局限于某幾個固定點位，無法擴展至整個海域；或注重海溫反演模型的建立，其反演模型是基于實測站位建立的，但研究選取的實測站位是否可代表整個海域有待商榷，同時也缺乏對長江口海溫時空演變模式的模態分析。

20世紀以來，遙感技術迅速發展，借助遙感手段可獲得長時序、全覆蓋的SST數據。但因云層、霧、霾等影響，常常出現數據缺失問題，為獲得具有連續時間序列的全覆蓋衛星遙感資料，國內外已有多種數據插值方法，如克里金插值法、最優插值法、期望最大化法、奇異譜方法、本征模態分解法、卡爾曼濾波法等。其中大多受限于數據的原始狀況，或依賴相關的參數和先驗值等信息，在適用性以及計算效率上均受限制。經驗正交函數分解法（data interpolating empirical orthogonal functions，DINEOF）是目前較為有效的遙感數據重構方法，具有無需先驗值、自適應、時空相關，以及適用于大面積缺測數據重構等傳統重構方法不具備的優勢［9-10］。

動態模態分解（dynamic mode decomposition，DMD）是Schmid于2008年提出的一種數據分析方法，其本質是將高維非線性系統矩陣轉化為低維線性系統的過程，已被廣泛應用于股票價格預測、圖像壓縮處理、物理流場分析等數據處理研究［11-13］。當數據的缺失率過高時，DINEOF具有很好的重構效果，在能夠獲得足夠時序數據的情況下，數據驅動的算法能夠更好地解決動態系統的采樣問題。海洋是一個典型的高維動態系統，尤其在近岸區域，受潮汐、風浪等因素影響，數據隨時間動態變化劇烈。因此，可將其視為由許多不同頻率的組分組成，DMD算法求得的模態和特征值分別描述了系統的空間特性和時間特性，符合相關海洋表面溫度研究的要求。DMD按照頻率對系統進行排序，提取系統特征頻率，觀察不同頻率的流場結構對流場的貢獻，同時DMD模態特征值可預測流場［14］。在能夠獲取足夠時序數據的情況下，DMD算法可以更好地解決動態系統的采樣問題，從而實現對海洋表面溫度的預測。

在實際應用中，由于數據維度高、樣本數量大、數據本身存在噪聲等問題，DMD算法需針對具體應用場景做相應改進。考慮海洋學的研究特性，為節約成本、提高效率并為實際站位布設提供參考，本文擬結合正交三角（orthogonal right triangular，QR）分解算法［15］通過典型觀測站位還原SST時空分布情況，進行精度校驗，并與單一DMD算法進行比較。

本文采用2003年1月至2019年12月MODIS L3級月平均SST遙感數據，主要開展兩方面工作：（1）用DMD算法獲得SST基本模態，并結合QR分解算法獲得典型觀測站位；（2）分別利用DMD算法、DMD結合QR分解算法對SST數據進行重構，并評價2種算法的重構精度，對誤差原因進行初步分析。

1 研究區域概況

如圖1所示，研究區域位于118°E～128°E，26°N～34°N，為長江口及其鄰近海域，區域內主要入海河流為長江和錢塘江等。長江口區域位于東亞季風區，夏季盛行西南風，冬季盛行東北風。水文結構一方面受近岸的長江沖淡水和沿岸流影響：北有低溫、低鹽、高沙的黃海沿岸流沿蘇北南下，西有低鹽、中沙的長江沖淡水輸入，其影響范圍存在季節性差異；另一方面受外海的臺灣暖流和黑潮次表層水的相互作用，兩者從臺灣島附近侵入，沿約200 m等深線北上，控制陸架外緣地區，但存在明顯的季節性差異［16-17］。此外，長江沖淡水與臺灣暖流混合水團的鹽度梯度明顯，主要影響長江口外羽狀鋒區域［18-19］。除季風與環流相互作用外，長江口區域還受潮汐、風浪等因素影響，導致長江口區域的水動力環境較為復雜，進而影響SST的時空分布。

圖1 研究區域地理位置示意［16-17］Fig.1 Geographical map of the study area［16-17］

2 數據和方法

2.1 MODIS/SST

MODIS中分辨率成像光譜儀是一種“圖譜合一”的光學儀器，可獲取從可見光到紅外共36個波段的觀測數據，其最大空間分辨率為250 m。MODIS可提供包含陸地、海洋、云、大氣、溫度等特征信息的數據產品，廣泛用于陸地、海洋及大氣環境監測等領域［20］。

考慮數據的時間連續性、適中的空間分辨率以及獲取數據的便捷性，選用2003—2019年MODISAqua遙感器的L3級月平均SST產品，數據從https：//oceandata.sci.gsfc.nasa.gov/獲取。空 間分辨率為4.6 km×4.6 km，每幀影像大小均為240×192，時間幀為204幀，各參數的觀測像元總數均為9 400 320個，且均采用NetCDF4格式。NetCDF4是一種科學數據存儲格式文件，能分層存儲數據，且可用C、Fortran和MATLAB等語言進行操作。

前處理主要包括掩膜制作、數據缺失率統計及空白數據填補、去噪處理等。

首先，獲取全球海岸線shp文件（網址：https：//www.ngdc.noaa.gov/mgg/shorelines/data/gshhs），導出研究區域的shp文件，并將導出的shp文件在ARCMAP中進行完善。然后，在MATLAB中將shp文件轉化為矩陣格式掩膜，令陸地部分為0，海洋部分為1，為方便處理，將陸地中的湖泊和河流賦值為0。掩膜處理完成后，統計海洋數據，數據缺失率為1.57%。因數據缺失率較低，考慮程序的運行效率，用每幀的平均值填補空白數據。最后，對填補完成的數據進行去噪處理。

2.2 DMD算法原理

將海洋視為由不同頻率的組分組成的高維非線性系統，由DMD算法得到的模態描述其空間特性。下面介紹DMD算法的原理。

首先，從數值仿真或實驗中收集N個時刻的快照，形成數據矩陣{ψ0，ψ1，…，ψN}，第i個時刻的快照為第i列，假設上述數據矩陣在時間上是等距的，時間步長為Δt。利用快照序列構建2個時間相鄰數據矩陣：

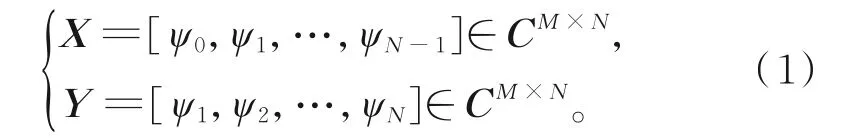
利用連續快照之間的線性關系，通過矩陣A將式（1）中的2個快照矩陣相連接。矩陣A為高維系統的系統矩陣，包含大量動態關系，反映系統的動態特征。由于矩陣A的維數高，需要對其進行降階處理。動態模態分解提供了矩陣A的低階表示方法：

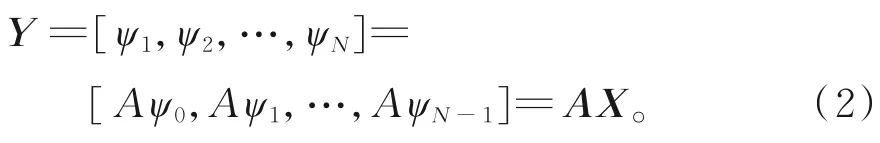
DMD通過對上述快照矩陣進行數學變換，提取主導特征值及主要模態。本征正交分解（proper orthogonal decomposition，POD）又稱主成分分析，將高維系統表示為少量POD模與其對應系數的線性組合，從而實現對高維系統降維。本文擬采用奇異值分解與POD相結合的方法，通過奇異值分解對高階算子進行相似變換，此方法具有較好的數值穩定性。

利用X的POD模，尋找秩為r的矩陣F，近似表示高維矩陣A：

其中，U為通過對X進行奇異值分解所獲得的POD模，U*為酉矩陣，有

其中，Σ為對角矩陣，對角線元素為r個奇異值，對應特征值σ1，σ1，…，σr，同時奇異值分解得到的酉矩陣U和V滿 足：

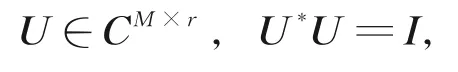
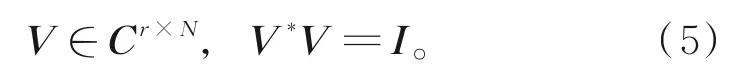
F的求解過程可看作將X和Y之間的Frobenius范數最小化，將式（3）和（4）代入，得到

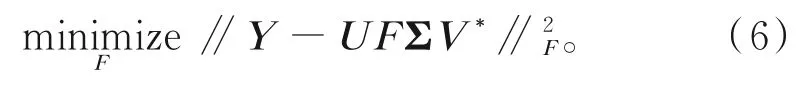
求解式（6），得到

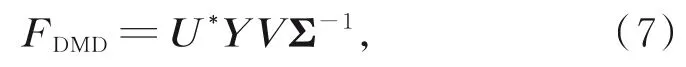
可用F近似表示A，記F的第i個特征值為μi，特征向量為ωi，則第i個DMD模態為

由以上定義可知，模態是所研究的系統中具有某種全局特征的結構，本文研究的全局特征是SST的“頻率”，即SST的變化率。另外，若特征向量為實數，則對應的特征向量隨特征值的正負變化分別呈指數級增長或衰退。

2.3 DMD結合QR分解算法確定典型觀測站位

DMD算法僅能解決理想情況下流場基本模態的獲得及預測問題。在實際應用中，由于數據維度高、樣本數量大、數據本身存在噪聲等，需根據具體應用場景對DMD算法做相應改進。QR分解算法用以求解矩陣特征值，可提高求解速度。用QR分解算法選擇典型觀測站位的思路是，對于給定的典型觀測站位數k，通過尋找最佳置換矩陣最大化|detAk|（det為矩陣的行列式值，Ak為QR分解算法中的上三角矩陣），尋找穩定、準確的典型觀測站位［21］。考慮海洋學的研究特性，本文擬結合QR分解算法計算最佳模態數和典型觀測站位數，利用典型觀測站位還原海溫數據。

2.4 數據處理流程

數據處理流程如下：

（1）下載原始數據，構造矩陣。用制作好的掩膜，剔除每個時間幀原始數據中的陸地和島嶼，只保留海洋部分的數據，計算平均值，用平均值替代其中的NaN（not a number），最后展開為列向量，有效數據共n個。對數據進行去噪處理，同時以p次間隔（p=204，時間間隔設為一個月）的觀測數據構建矩陣Xp×n，時間設定為起始時間t1到結束時間tq，且滿足tq=tq-1+Δt。

（2）抽取前80%的連續數據作為訓練數據，數據量為m（m=163，時間間隔為一個月），其余的20%作為預測數據，數據量為q（q=41，時間間隔為一個月）。

（3）由上述訓練數據矩陣Xm×n構造子矩陣。令子矩陣的時間間隔為Δt，得到Xm-11，Xm2：

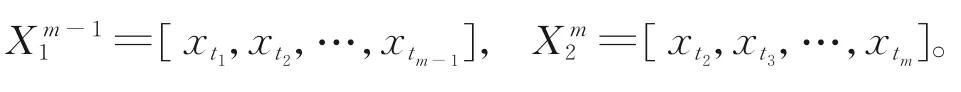
（4）求特征值和特征向量。經步驟（3）后得到2個子矩陣，對X1m-1進行奇異值分解，Σ、U、V*分別為奇異值、左奇異向量、右奇異向量，同時結合矩陣計算低階矩陣F的特征值及其特征向量。

（5）將得到的特征值和對應的特征向量組成矩陣，根據QR分解算法，確定最佳模態數和最佳典型觀測站位數，并將其代入FDMD中，重構歷史數據。

3 結果與討論

3.1 長江口長時序SST的DMD模態分解

利 用2003—2019年 的MODIS L3級 月 平 均SST產品，由DMD得到SST的主要時空演變模態，用這一典型非線性動力學現象說明DMD在海洋系統中的應用過程。訓練數據的時間段為2003年1月至2016年7月，預測數據的時間段為2016年8月至2019年12月。

將DMD結合QR分解算法尋找典型觀測站位的方法（以下簡稱典型觀測站位還原法）應用于上述訓練數據，得到的重構誤差與典型觀測站位數的關系如圖2所示。

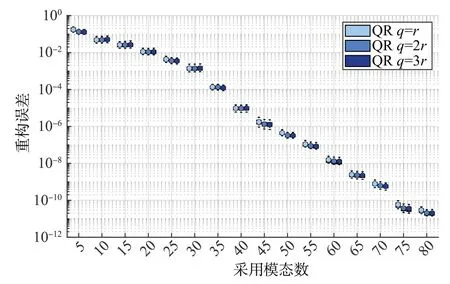
圖2 典型觀測站位效果對比Fig.2 Comparison of effect of typical observation stations

其中，重構誤差用均方根誤差（root mean square error，RMSE）表征，p表示典型觀測站位數，r表示DMD模態數。由圖2可知，均方根誤差隨DMD模態數的增加而降低，且若DMD模態數不變，通過增加典型觀測站位數能有效降低重構誤差。DMD算法得到的主要模態如圖3所示（因篇幅所限，此處只給出前4個模態）。

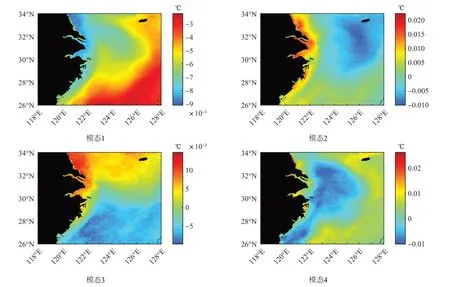
圖3 用DMD算法分解長江口海域SST數據得到的前4個主要模態Fig.3 The first four main modes decomposed by DMD algorithm of SST data in the Yangtze River Estuary

由圖3可知，模態1在整個海域表現為負相關，從空間分布看，蘇北沿岸、長江口及杭州灣和浙閩沿岸區域是SST變化率絕對值較大的區域，變小很快，且隨著長江沖淡水的外推呈舌狀遞增狀態，而SST變化率絕對值較小值出現在沖繩島西北海域的大洋區域，變小很慢。推測出現這種分布的原因可能由近岸區域受陸地徑流輸入的淡水與海水混合所致，而低值區受黑潮和臺灣暖流影響，海水性質比較均一。季節特征表現為由秋入冬。

模態2中SST變化率與近岸區域及南側海域呈正相關、與中北側海域呈負相關，表明2個區域呈現相反的變化趨勢。這可能反映地形對SST的影響，蘇北沿岸、長江口及杭州灣、浙閩沿岸區域水淺、比熱容小，易受大陸氣溫和沿岸流的影響，SST變化率最大值高于0.02℃，呈現SST變大、變快的特征；南側海域受黑潮和臺灣暖流的影響，表層SST變化不大；中北側由于遠離陸地，受環流影響小，SST變化率呈負值。季節特征表現為由春入夏。

模態3中SST變化率呈正、負2種分布情況，蘇北沿岸、長江口及杭州灣、浙閩沿岸區域及北側海域為正值區域，南側海域為負值區域。這與第1模態所反映的受沖淡水、環流的影響相同。但季節特征表現為由春入夏。

模態4則表現為近岸部分和150 m等深線以外的大洋區域為SST變化率正值區，大致為被30 m和150 m等深線所夾區域為SST變化率負值區。這與第2模態反映的地形影響一致。但季節特征表現為由秋入冬。

3.2 DMD結合QR分解算法獲取典型觀測站位

上述結果表明，當DMD模態為25、典型觀測站位為25時，重構誤差已經相當小。因此，考慮運行速度和重構精度，本文選取25個DMD模態、25個典型觀測站位對長江口海域的海表溫度進行稀疏還原，結果如圖4所示。

圖4 2016年8月長江口海域SST數據稀疏還原結果Fig.4 The results of sparse restoration of SST data in Yangtze River Estuary in August 2016

由圖4可知，相比單純采用DMD算法，DMD結合QR分解算法的還原結果能很好地代表整個海域，海溫分布與真值更接近。因此，若不考慮成本和運行速度，單一追求重構精度，用DMD算法能得到更高精度的還原結果。若綜合考慮成本、運行速度、重構精度，則DMD結合QR分解算法的重構表現更佳。

3.3 精度分析

選取2016年8月相同區域的原始數據與重構數據的像元值進行精度評價，評價結果如圖5所示。從圖5（a）和（b）的對比中可知，2種方法的原始值與重構值集中分布在直線y=x附近，精度指標均較理想。其中，DMD結合QR分解算法的RMSE為0.005 0。據統計結果，測試數據集的歷史數據與DMD結合QR分解算法重構數據之間的RMSE在0.005 0～0.011 2，平均值為0.007 6。因此，雖然在精度上DMD算法的最佳還原結果比DMD結合QR分解算法的還原結果表現更佳，但考慮運行速度和成本，仍可認為DMD結合QR分解算法的結果較好。

另外，由圖5可知，無論是DMD算法還是DMD結合QR分解算法重構得到的結果均具有相當高的精度。為進一步分析重構效果，隨機選取2個典型觀測站位，對其原始值、DMD最佳還原值、典型觀測站位還原值做對比分析。

由圖6可知，DMD最佳還原值和典型觀測站位還原值與原始值耦合良好，說明DMD算法和DMD結合QR分解算法均較合理可靠。因此，可以認為選取的25個典型觀測站位能較好地代表整個研究海域海洋表面溫度的分布特征。這與圖5的DMD算法和DMD結合QR分解算法的結果高度吻合。

為更好地評價2種方法的重構效果，選擇預測數 據 集 中 的2017年4月、2017年7月、2017年10月及2018年1月（分別代表春、夏、秋、冬4個季節）進行重構，得到的結果如圖7所示。

由圖7可知，從空間分布上看，2種方法的重構結果均與原始值的趨勢保持一致，誤差較小，這與圖5和圖6得到的結論一致。

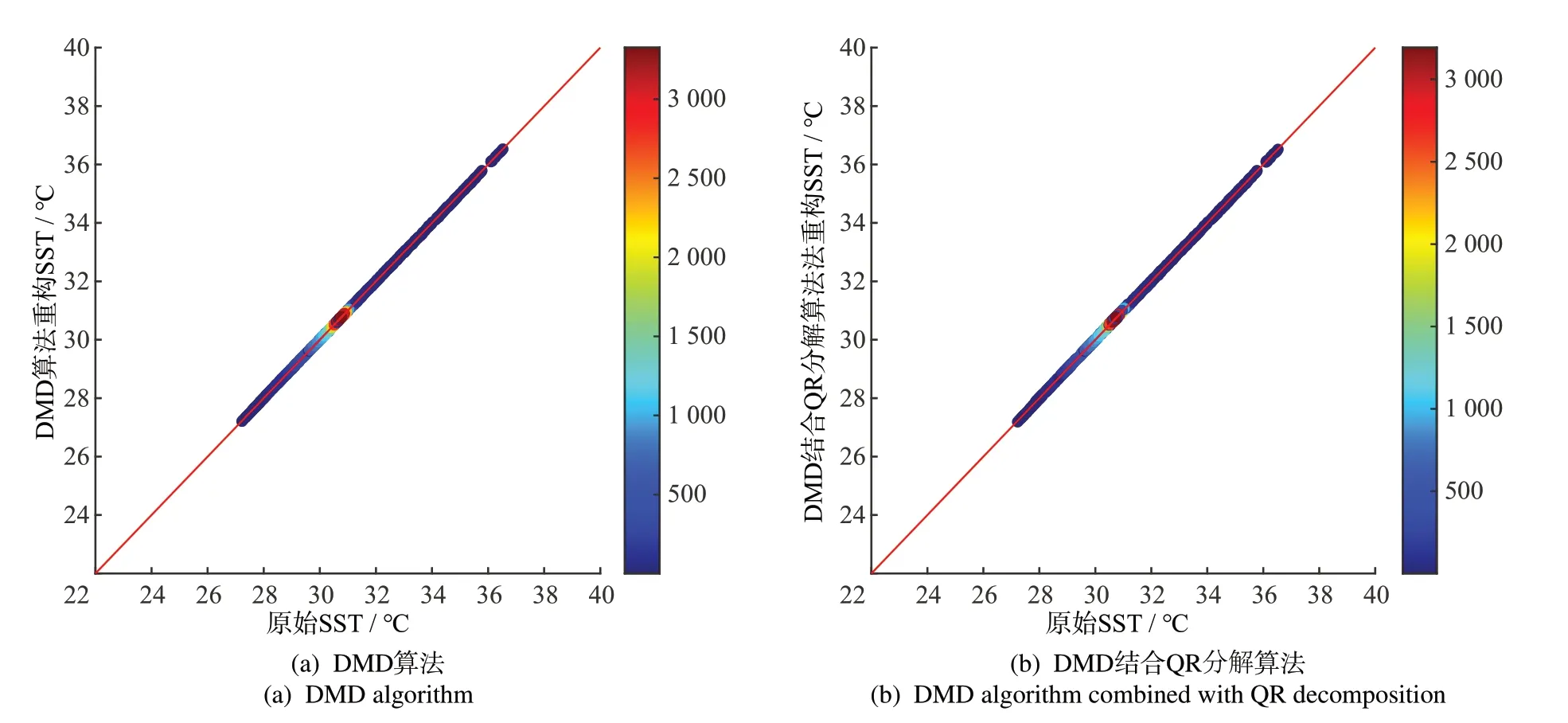
圖5 2016年8月的SST重構精度Fig.5 The accuracy of SST reconstruction in August 2016

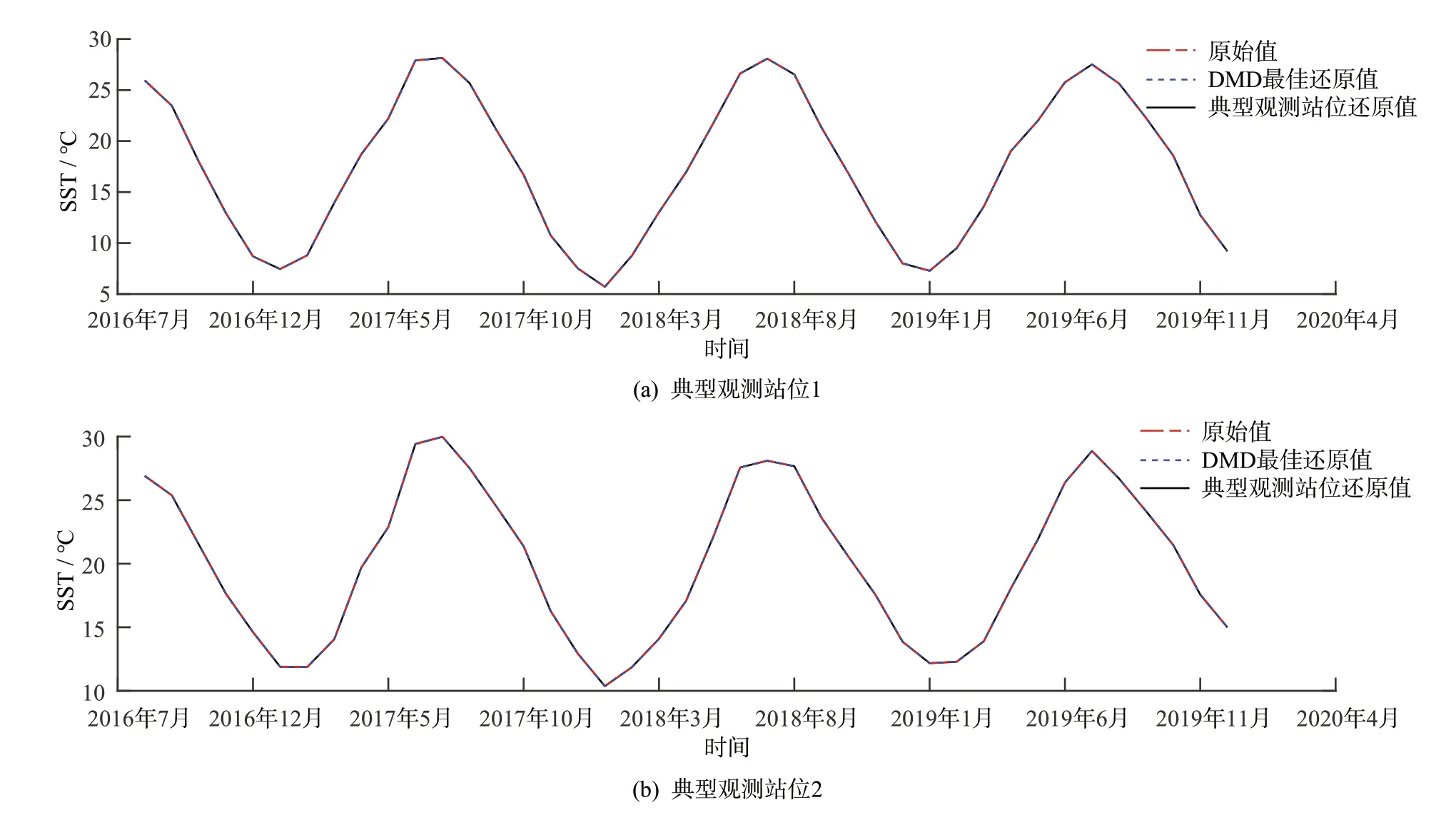
圖6 某2個典型觀測站位重構前后對比Fig.6 Comparison of reconstruction of two typical observation stations

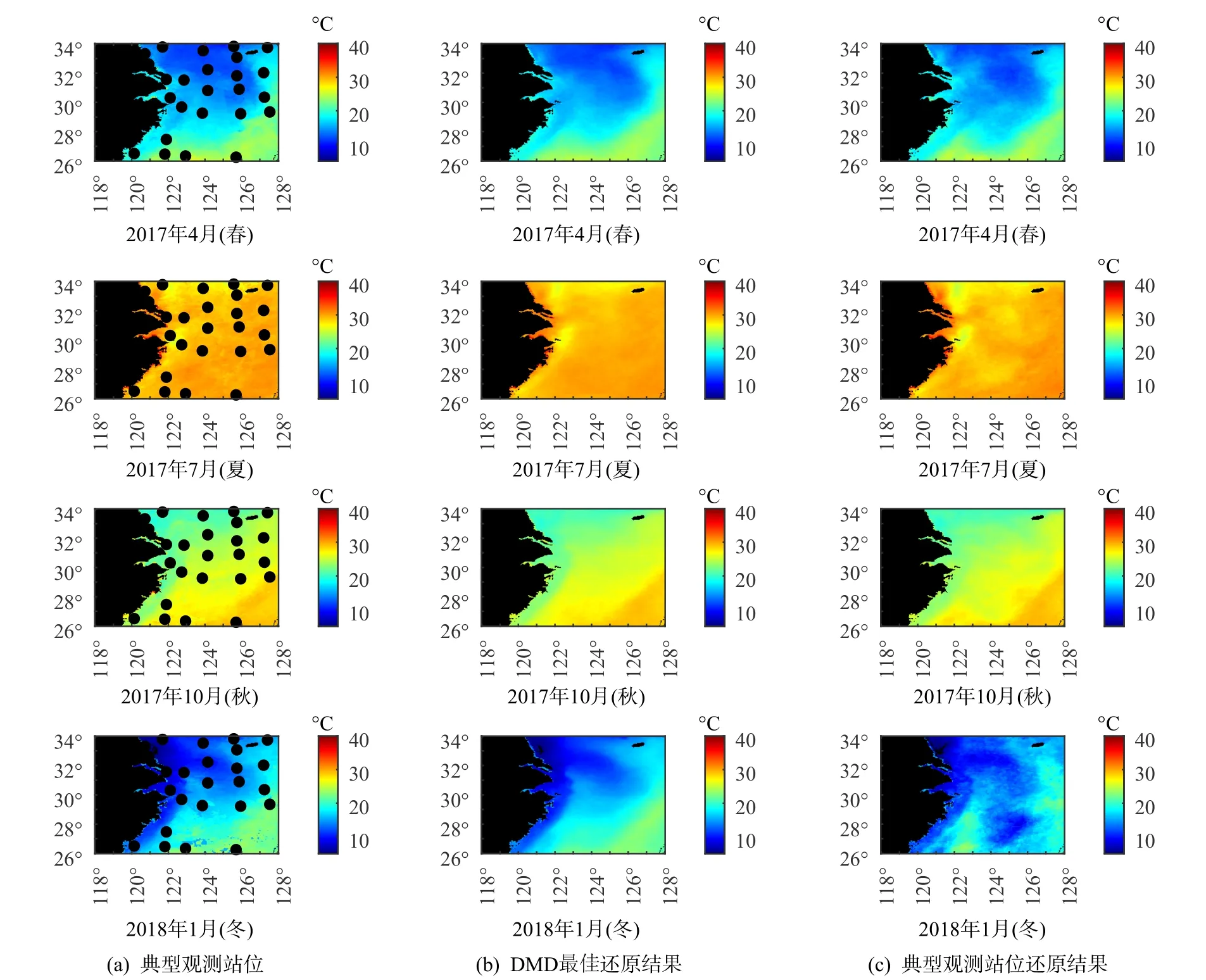
圖7 長江口海域典型年份四季SST數據稀疏還原結果Fig.7 Sparse restoration results of SST data in four seasons of a particular year in the Yangtze River Estuary

4 結論

基于DMD算法的基本理論，將QR分解算法應用于海洋學觀測，分析了長江口海域的海溫數據。結果表明，DMD結合QR分解算法對長江口海溫數據進行稀疏還原，能有效去除噪聲，填補缺失數據。增加DMD模態數能有效降低重構誤差，當模態數一定時，可通過增加典型觀測站位數降低重構誤差。當采用25個模態、25個典型觀測站位時，重構數據的RMSE為0.005 0。

DMD算法分解得到的前4個模態中，模態1和模態3可能反映了長江沖淡水及環流的影響，模態1的季節特征為由秋入冬，模態3則為由春入夏；模態2和模態4可能代表海底地形的影響，模態2季節特征為由春入夏，模態4則為由秋入冬。

在數據充足的情況下，DMD算法能很好地解決動態系統的采樣問題，對時序數據的重構和分析具有應用價值。單純采用DMD算法重構，精度相對較高，但采用DMD結合QR分解算法重構效率較高，并且可在稀疏站位條件下重構海洋溫度場，這對海洋學調查尤為重要。