基于性態的液化場地多跨橋梁樁基地震響應分析

惠舒清，唐 亮，凌賢長，，蘇 雷，李雪偉，滿孝峰

（1.哈爾濱工業大學土木工程學院，哈爾濱，150090；2.青島理工大學土木工程學院，青島，266033）

引言

地震是最重要自然災害之一。地震對橋梁工程等造成的巨大破壞，常常為災后救援重建工作帶來諸多困難。一系列的震害調查顯示，強震引發的場地液化誘發樁基礎出現塑性鉸是導致橋梁破壞的重要原因［1～3］。對于樁基橋梁，地震中液化場地樁上受到的側向荷載主要有運動荷載和慣性荷載［4～7］。過去發生一系列大地震所造成的重大損失使國內外學者意識到，過去僅以防治結構損傷為目標的抗震設計是遠遠不夠的［8～13］。基于此，美國學者針對結構工程，率先引入基于性態的抗震設計思路（Performance-based Seismic Design），根據設防水準劃分不同的抗震性態等級，結合結構使用功能實際情況，合理地確定抗震性態的設計目標并給出合適的結構抗震措施。

目前，圍繞橋梁結構的基于性態的地震工程設計中，許多研究者開展了相關研究工作。KRAMER［14］全面回顧了基于性態的地震工程的產生和發展，給出的基于性態設計中常用的基本概念和未來可能遇到的挑戰和機遇；SHIN 等［15］基于性態的地震工程研究了液化場地橋梁的抗震特性；類似，KRAMER 等［16］對液化場地橋梁樁基采用基于性態的地震工程方法進行了分析；LEDEZMA 等［17］給出了基于性態的地震工程設計方法，此方法能夠很好估計側向擴流場地樁支結構地震特性；ELGAMAL 等［18］發展了基于性態的橋梁樁基抗震分析計算平臺BridgePBEE（https：//peer.berkeley.edu/bridgepbee），該平臺可準確考慮樁－土－結構動力相互作用并可以進行整個樁基橋梁結構的性態評估。并基于此平臺，考慮耦合的樁－土－橋梁結構體系，采用基于性態的地震工程評估方法研究了典型高架橋梁在不同場地的地震特性；BRADLEY 等［19］等對樁－土－橋梁結構體系進行概率地震響應分析和損失評估。結果表明：非水平的土層結構、場地液化和土－結相互作用顯著地影響著橋梁各部分的地震需求特性；MACKIE等［20］在基于性態的地震工程框架內，獲得樁基橋梁的優化概率地震需求模型；類似地，SHIN 等［21］建立了液化場地樁基橋梁的數值模型用于評估橋梁地震特性。以上分析可知：基于性態的抗震設計已經在橋梁工程領域得到廣泛的應用，如，然而針對液化場地樁基地震響應分析方面應用較少，特別是多跨橋梁結構。鑒于此，本文針對液化場地多跨簡支樁基橋梁體系，參考KRAMER 和JALAYER［22］的分析方法，考慮地震隨機性的不確定性和認知的不確定性，結合地震危險性曲線自身的不確定性，推導性態指標危險性曲線的解析表達式。在建立的多跨橋梁體系數值模型的基礎上，進行大量的數值模擬。根據數值模擬結果，選取地震過程中關鍵位置的位移和彎矩最大值作為性態指標的響應，通過在雙對數坐標下進行線性擬合，得到不同性態指標的地震需求模型和地震危險性曲線，進而分析其響應特性。

1 變量不確定性來源

通常變量的不確定性主要來源兩個方面：第一方面是由于認知能力的不足引起的不確定性，主要受當前認知水平的限制；第二方面是由于變量自身的不確定性所致。所以，對于一個特定的變量X，可以采用下面的模型考慮這兩類不確定性。

2 基于性態設計方法

一般，基于性態的抗震設計方法，主要采用簡化的數值模型來減少計算機時。因為基于性態的設計方法往往要進行大量數值計算，特別是對于巖土工程結構。近年，隨著計算機技術的迅速發展和并行技術的日益成熟，基于性態的設計方法得到快速發展，特別是采用有限元方法。基于性態的抗震設計方法主要包括以下步驟：（1）性態指標選取；（2）地震動危險曲線確定；（3）地震動需求模型確定；（4）性態指標危險性曲線確定。以下主要基于上述4個方面展開討論與分析。

2.1 性態指標的選定

這里選定整個體系的性態指標見圖1和表1。這些指標即地震需求變量（Demand Variable，DV）。從表1可見：選取的這些地震需求變量主要分為兩類：一類是位移；另一類是彎矩。這兩類響應也是工程師在工程設計中最關注的響應。考慮模型上部橋面板剛度很大和模型的對稱性。位移響應，主要選取橋臺頂、柱墩頂和承臺位移及土層分界處樁的位移；彎矩響應，主要選取橋臺頂、柱墩頂的彎矩和群樁頂、群樁底和土層分界處樁的彎矩。對于位移和彎矩響應，可以通過建立的數值計算模型，在不同地震動激勵下得到，其值實際為其時程響應最大值。

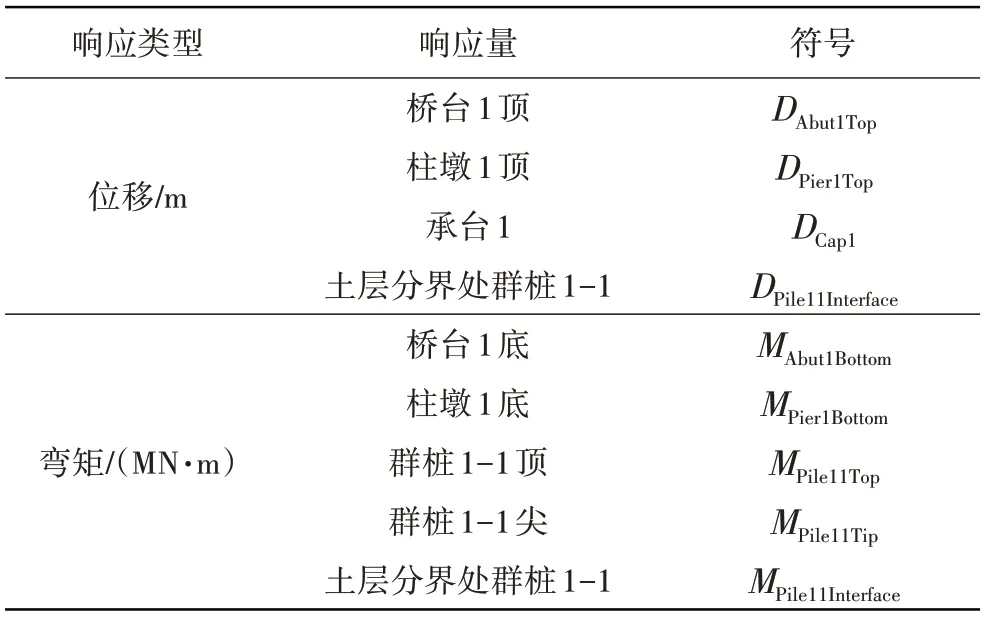
表1 多跨橋梁體系地震需求變量Table 1 Seismic demand variable of multi-span bridge system

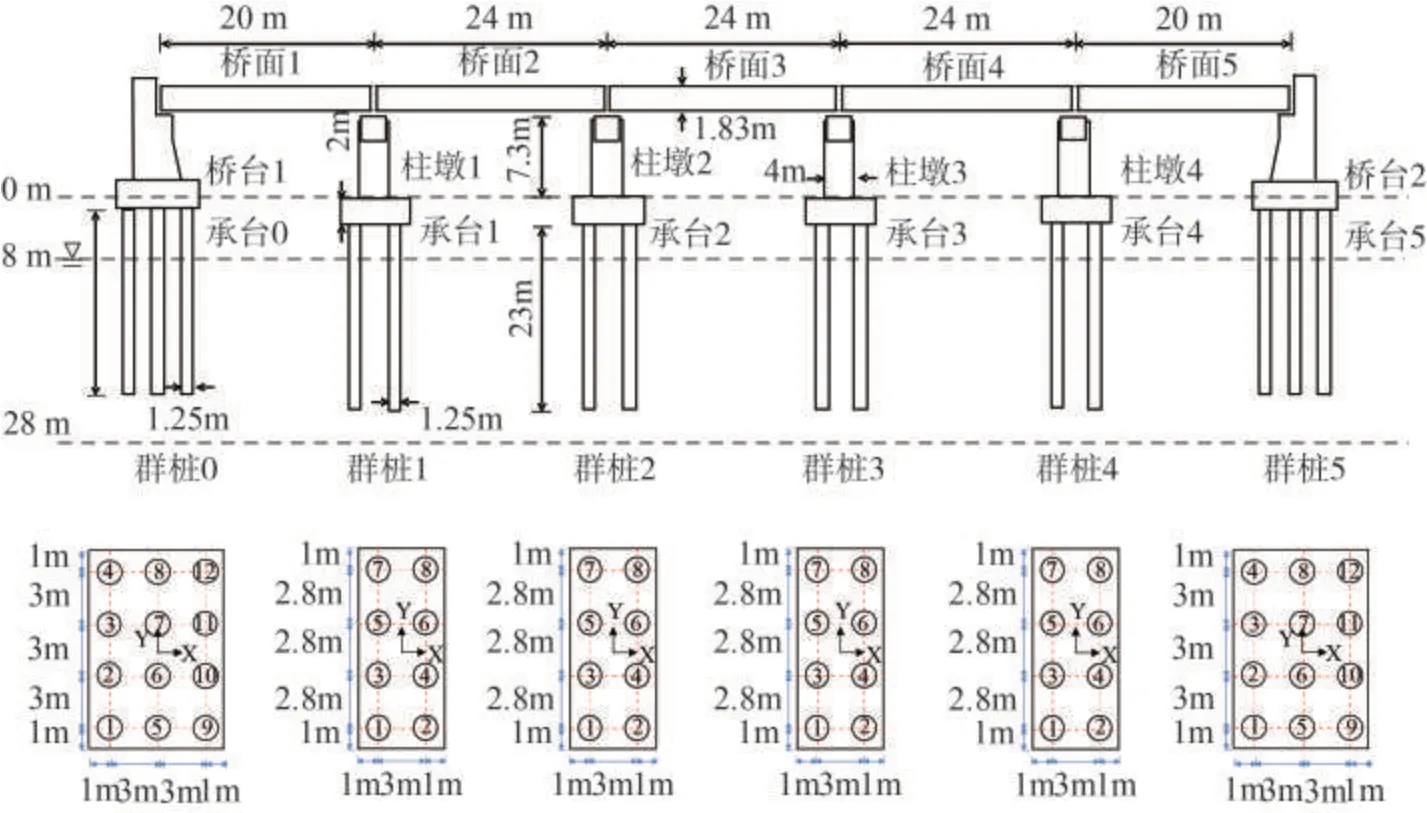
圖1 多跨橋梁體系布置示意圖Fig.1 Layout of multi-span bridge system

2.2 地震危險性曲線的確定

地震危險性曲線（Seismic Hazard Curve）確定非常復雜。通常，由地震學家通過地震危險性分析得到，地震危險性分析主要針對特定場地的地震動危險性進行定量的評估。KRAMER［23］詳細給出了地震危險性分析的步驟。美國部分場地可以從USGS（http：//www.usgs.gov/）得到相應的場地地震危險性曲線。下面結合我國《建筑抗震設計規范》（GB50011-2010），參考前期研究成果［24］，得到以PGV/PGA（為了方便表示，本文采用R表示PGV/PGA）為強度指標的地震危險性曲線，其中：PGA 為峰值地面加速度（Peak Ground Acceleration），PGV 為峰值地面速度（Peak Ground Velocity）。

通常，需要通過地震危險性分析，確定出特定地區的地震危險性曲線。這里僅根據不同設計基準期對應不同烈度值得到對應的峰值速度和峰值加速度的比值R，進而通過R與年平均超越概率進行擬合。通常，近似認為某地區的地震危險性曲線為指數形式分布［25］。正常情況下，危險性曲線需根據場地條件、斷層條件且通過地震危險性分析進行確定，然而在進行地震危險性分析時仍進行大量的假設。下面考慮以R表示的危險性曲線的不確定性。若采用相同的指數形式的表達式作為不確定性危險性曲線的中位數的估計，并引入隨機變量εUH代表危險性曲線的不確定性，并假定εUH服從對數正態分布。由于地震危險性曲線HR(x)本身為隨機變量，所以HR(x)可以表示其自身的中位數與隨機變量εU的乘積，所以，HR(x)的平均值-HR(x)可以表示為：

2.3 地震動強度指標與性態指標之間經驗關系

為了確定地震動指標（R）與性態指標（如，Dhead）之間的關系，需要輸入不同的地震動，進行相應動力時程響應分析，得到性態指標的響應。所確定的這種關系稱為地震需求模型（Seismic Demand Model，SDM），通過地震需求模型，給定地震動強度指標值的情況下，近似估計性態指標的值。然而，對于相同幅值的地震動，性態指標的響應存在一定差異性。假定這種差異性主要由于地震動的隨機性導致。所以，這里引入R與性態指標中位數的函數關系式，并考慮性態指標中位數由于地震動隨機性引起的差異性，引入隨機變量εRD解釋這種差異性。為了簡化分析，采用類似地震危險性曲線的指數形式擬合R值與性態指標DV中位數關系。進一步，由于性態指標的中位數也具有不確定性，這種不確定性主要是由于認知的不確定引起，比如數值模型不確定性、模型參數的精確性等。為了考慮這種認知的不確定性，性態指標DV中位數可以表達為其中位數的估計值與認知不確定性離散變量εUD的乘積，可以得到：

假定εUD和εRD是相互獨立的，且服從對數正態分布，這里，μDV(x)稱為在給定R值下，性態指標的中位數的值，也記為μDV|R(x)。

2.4 性態指標危險性曲線的確定

首先，只考慮性態指標的中位數由地震動隨機性引起的差異性，可以得到：

因為假定隨機變量εRD服從對數正態分布，可以得到性態指標DV也是服從對數正態分布的隨機變量。

進一步假定在給定R值情況下，性態指標DV的條件中位數近似用指數函數關系進行表述，然而性態指標DV自然對數的條件標準差σlnDV|R(x)是常數。

性態指標DV為不同地震動輸入下計算的性態指標的最大值響應。類似于地震危險性曲線，性態指標的危險性曲線定義為性態指標DV超過特定需求值dv的年平均概率，利用全概率公式，分解給定R情況下，性態指標DV超過特定需求值dv的概率和R等于特定值x發生的概率，然后對不同R值求和，引入R的概率密度函數fR（x）與互補累積分布函數G（x）。注意到：（1）地震危險性曲線HR（x）等于R 的互補累積分布函數GR（x）與地震年平均發生率ν 的乘積；（2）性態指標DV也服從對數正態分布，即lnDV服從正態分布；（3）隨機變量的對數的平均值等于平均值的對數。采用分部法進行積分，并考慮在地震危險性曲線的不確定性εUH和性態指標認知的不確定性εUD，推導得：考慮由于地震的隨機性引起的不確定性和認知的不確定，同時考慮地震危險性曲線的不確定，式（5）即為性態指標的危險性曲線的最終解析表達式。詳細的推導過程請參見文獻［22，23，26］。

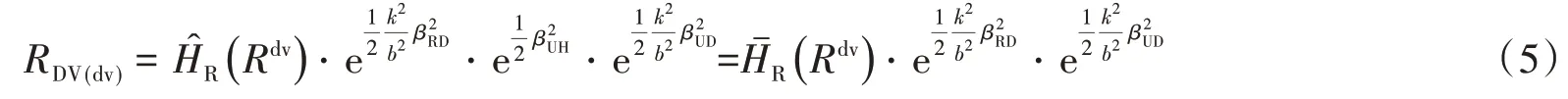
2.5 地震動的選取

基于上述分析，這里選取不同地震動作為基底輸入激勵，這些地震動的R的變化范圍從2.26 s到43.3 s，如圖2所示。

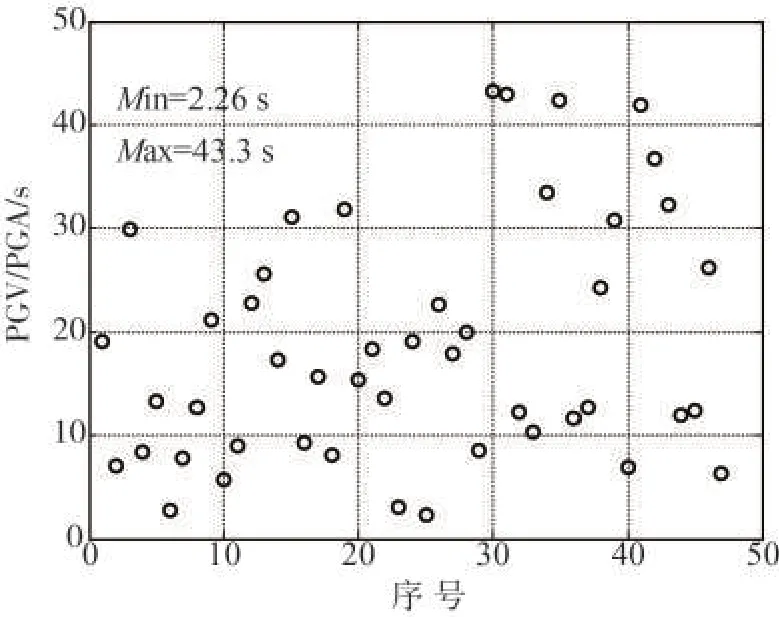
圖2 選取地震動PGV/PGA分布Fig.2 PGV/PGA value distribution of selected ground motion

3 采用的簡支梁橋及簡化數值模型

3.1 簡支梁橋簡介

基于圖1-2，借助MssSRA 數值計算平臺，建立多跨橋梁體系有限元數值計算模型。以某鐵路鋼筋混凝土五跨簡支梁橋為工程背景。橋梁總長度為112.0 m，五跨主要分成兩類，中間三跨具有相同的長度24.0 m，左右兩側跨跨徑為20.0 m。針對于橋面板，全部處于同一個平面上。橋墩則采用高度為7.3 m的單圓柱截面實心墩。橋墩截面采用截面直徑為4.0 m的等截面形式。橋臺采用重力式橋臺，橋臺寬度為8.2 m，上部背墻高度為1.83 m，下部承重墻高度為8.02 m，翼墻寬度3.965 m。等腰梯形截面的路堤與橋臺連接，沿橋縱向和豎向之比為其坡度為0.5，土質為回填砂土，密度為1 987.0 kg/m3，剪切波速492.0 m/s。承臺高度為2.0 m，橋臺和橋墩下布置鋼筋混凝土樁，樁徑為1.25 m，樁長為23.0 m。地基分為為兩層不同土，上層為松砂層（厚8 m），下層為密砂層（厚15 m）。地下水位線在地表處，上層土屬可液化土層。

3.2 簡化數值模型

針對上述梁橋結構，為了減小計算量，采用簡化的計算模型，土體和上部結構單元并沒有采用實體單元，如圖3 所示。通過將自由場土體的分析，將自由場地土體位移和孔壓作為外部激勵，將其輸入模擬樁－土界面的p-y宏單元［4］。

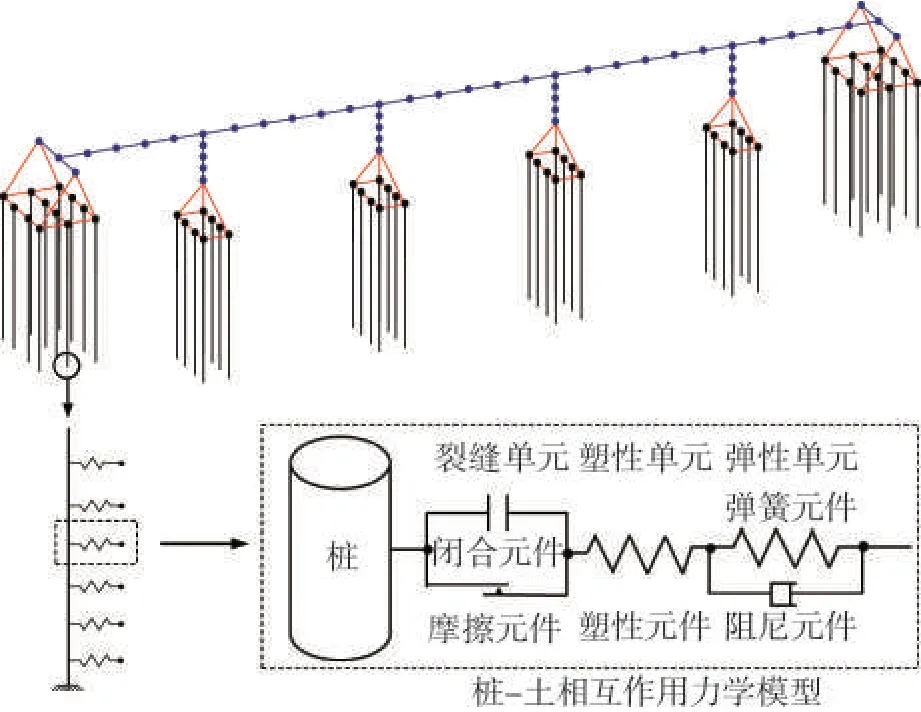
圖3 樁-土－橋梁結構體系三維有限元模型Fig.3 Three-dimensional finite element model of pile-soil-bridge structure system

其中：樁－土相互作用力學模型將彈性單元、塑性單元和裂縫單元串聯。其中：將彈性彈簧和遠場阻尼器并聯，能夠確保動力相互作用過程中輻射阻尼的作用；裂縫單元以雙線性的閉合形式彈簧和非線性物理模型搖曳彈簧組成，以模擬接觸-分離的實際作用過程。塑性單元采用“p-乘因子法”修正的砂土p-y曲線描述樁－土地震相互作用過程。這里，將其p-y曲線替換為考慮樁間距效應的液化場地樁－土地震相互作用p-y曲線［26］。橋臺采用AVIRAM 等［27］根據Caltrans 抗震設計規范（SDC2004）利用OpenSees 計算平臺調整修正得到的簡化模型。簡支跨中墩頂和橋面連接采用兩個零長度單元彈簧分別模擬縱向活動支座和固定支座。由簡支梁基本理論可知：相鄰橋面板之間在節點處允許發生相對轉動。因此，以彈簧描述相鄰橋面板直接的連接方式，綁定相鄰橋面板3 各方向的平動自由度，釋放其轉動自由度，允許相鄰面板之間發生相對轉動。地震作用下，由于橋面板（主梁）的應力主要保持在彈性階段，且地震破壞時主要集中在橋墩和樁上。因此，橋面板采用剛度較大的線彈性梁單元模擬。分析中，承臺不易破壞，而且不滿足梁柱的平截面假定，其力學特性近似于剛體，因此采用抗彎剛度和抗壓剛度極大的線彈性梁單元模擬。

此外，選取了與本文模型基本相似的唐貞云等［28］在北工大開展的多跨橋梁試驗進行了驗證，通過Pushover 靜力分析法，發現橋墩桿端剪力以及彎矩分布規律均與試驗吻合較好，可知該簡化數值模型的適用性較好，詳見文獻［26］。

4 數值計算結果

通過對建立的多跨橋梁體系施加不同幅值的地震動，得到其不同性態指標（即體系關鍵位置的位移和彎矩地震響應）的地震響應時程，進而得到性態指標響應的最大值，通過雙對數的線性擬合，得到性態指標隨R 變化關系，即地震動強度指標與性態指標的關系（IM-DV 關系，地震需求模型），進一步考慮地震隨機性的不確定性和地震危險性曲線的不確定性，得到性態指標危險性曲線，見式（5）。

4.1 多跨樁基橋梁體系位移響應

圖4給出了橋臺、柱墩和承臺位移地震需求模型和危險性曲線，即性態指標與R關系和性態指標超越特定值的年平均超越概率。圖4中的a和b為將R和性態指標在雙對數線性擬合時確定的系數，而σ代表性態指標對數值的標準差。從圖4中不難看出：整體上位移隨著R的增大而增大，但是最大位移并沒有出現在最大的R處。利用擬合得到的系數a和b，進一步結合式（5），可以得到不同性態指標年平均超越概率。由圖4（a）可知：對于橋臺1頂的位移，隨著位移增加，年平均超越概率將變小。圖4（b）給出柱墩頂的位移地震需求模型和危險性曲線。與橋臺頂位移相比，柱礅頂的位移變化規律類似橋臺頂，但是相同位移下，其年平均超越概率要更大。表明達到相同位移情況下，柱墩頂年平均超越概率要大于橋臺頂，柱墩頂可能更容易出現破壞。圖4（c）給出了承臺1位移的地震需求模型和危險性曲線。整體上，承臺位移隨著R的增加在增大，其最大R并沒有對應地發生最大位移。其年平均超越概率隨著位移的增加而減小。

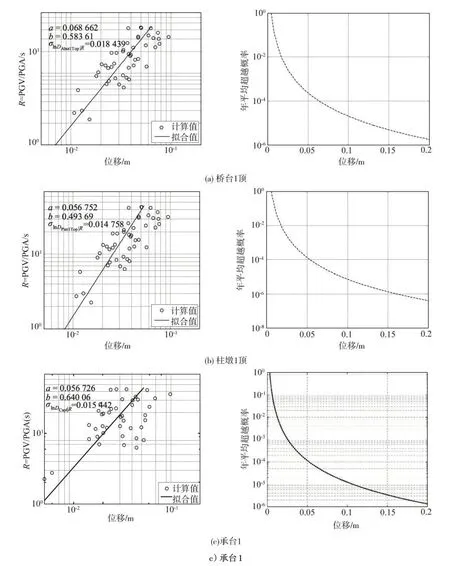
圖4 橋臺、柱墩和承臺位移地震需求模型和危險性曲線Fig.4 Seismic demand model and hazard curve of displacement on abutment，pier and pile cap

考慮到在歷次震害調查表明：在土層分界處，由于土體剛度的突變，往往會出現位移的突變，所以這里選用土層分界處樁的位移進行分析。圖5 顯示在土層分界處樁位移的地震需求模型和危險性曲線。整體上，樁的位移隨著R的增加而增大，其最大R幾乎對應著樁最大位移的產生。樁位移的年平均超越概率隨著位移的增加而減小。從計算結果可以看出：橋臺、柱墩和承臺的位移范圍均處于0.01～0.1 m范圍內，而樁的位移則集中于0.001～0.01 m，以R 等于10 為例，柱墩位移為0.024 m，樁基位移為0.004 m，柱墩位移是樁基位移的6 倍。柱墩位移和樁基位移均為0.1 m 時，柱墩對應的年平均超越概率（1.4×10－4）大于樁基對應的年平均超越概率（1.2×10-5）。

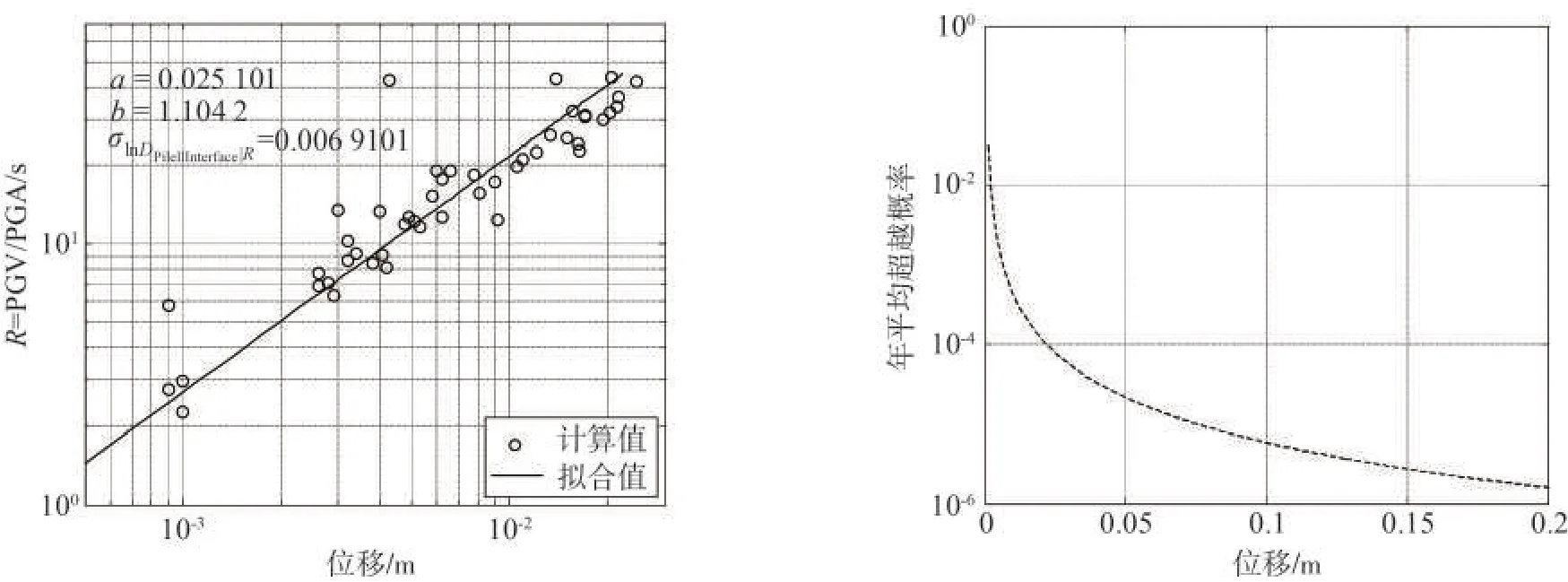
圖5 土層分界處群樁1-1位移地震需求模型和危險性曲線Fig.5 Seismic demand model and hazard curve of displacement on the No.1 of pile group 1 in the soil interface

從分析不難看出，整體上，相同R情況下，承臺、橋臺和柱墩的位移要大于樁的位移，其對應的年平均超越概率也較大。

4.2 多跨樁基橋梁體系彎矩響應

以下討論體系彎矩的地震需求模型和性態指標的危險性曲線。圖6（a）和（b）表示了橋臺1 底和柱墩1底的彎矩地震需求模型和危險性曲線。整體上，橋臺底和柱墩底的彎矩隨著R的增加而增大。同樣，其最大R并不對應著最大彎矩。類似地，橋臺底和柱墩底的年平均超越概率隨著彎矩的增加而減小。對比橋臺底與柱墩底彎矩的危險性曲線，不難發現，在相同彎矩下，柱墩底的年平均超越概率要大于橋臺底，即柱墩底更容易發生破壞。

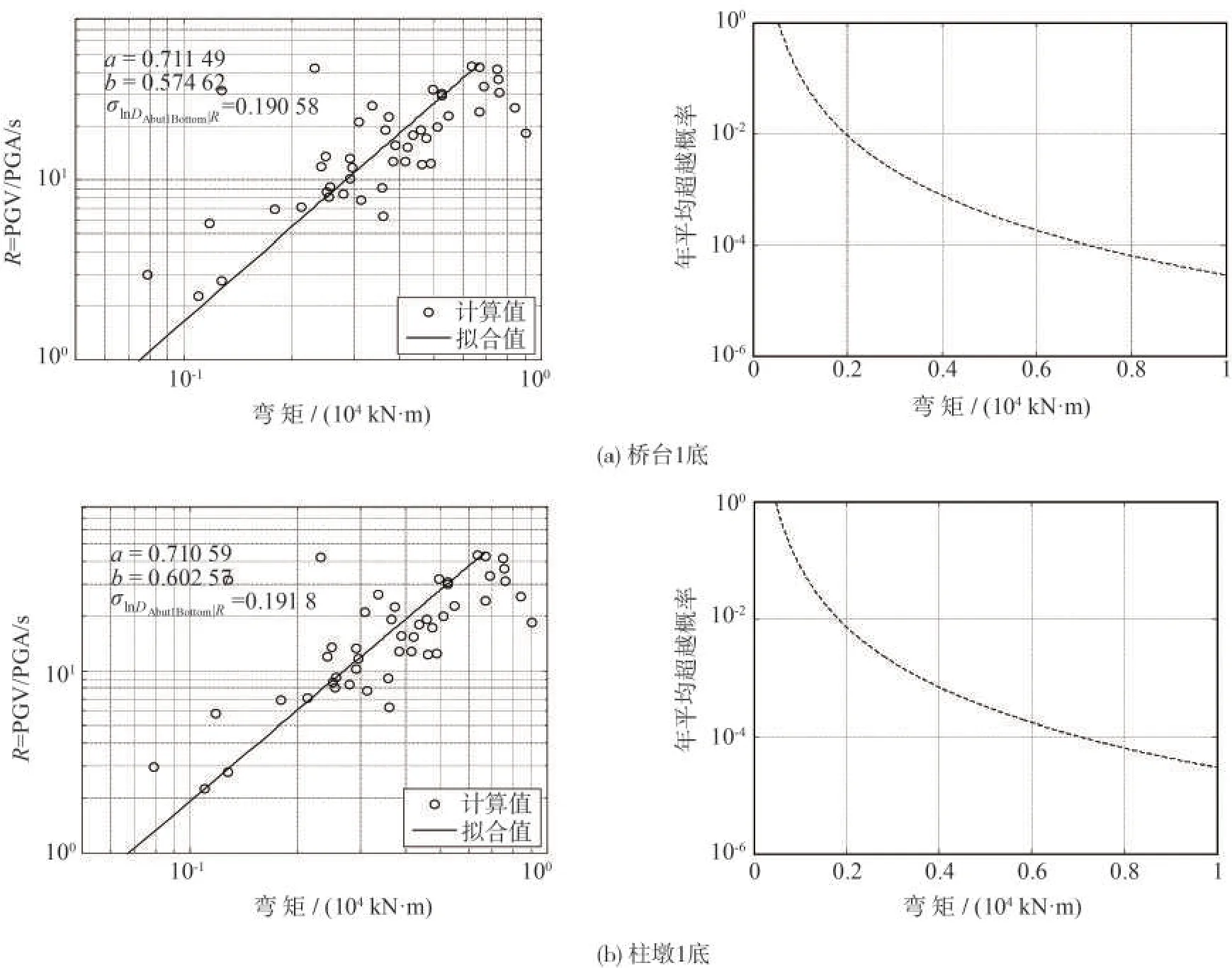
圖6 橋臺、柱墩彎矩地震需求模型和危險性曲線Fig.6 Seismic demand model and hazard curve of bending moment on abutment and pier

類似于土層分界面樁的位移，圖7（a）給出了不同群樁中基樁頂的彎矩地震需求模型和危險性曲線。整體上，基樁頂彎矩隨著R的增加而增大，其最大R并不對應著最大彎矩，而年平均超越概率隨著彎矩的增加而減小。

圖7（b）為群樁不同樁尖的彎矩地震需求模型和危險性曲線。整體上，在雙對數坐標系中，樁尖彎矩與R線性擬合較好，即對應的性態指標對數值標準差相對較小。同樣、樁尖彎矩隨著R的增加而增大，其最大值基本發生在最大R處。年平均超越概率隨著彎矩的增加而減小。圖7（c）給出在土層分界處基樁的彎矩地震需求模型和危險性曲線。整體上，在土層分界處樁彎矩地震需求模型和危險性曲線與樁尖處類似。

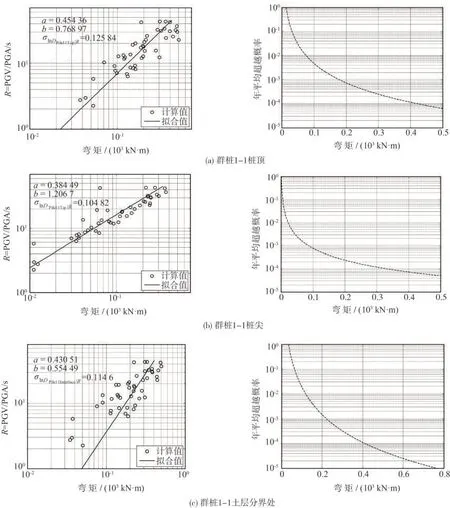
圖7 樁彎矩地震需求模型和危險性曲線Fig.7 Seismic demand model and hazard curve of bending moment on pile

綜上所述，可以看出：橋臺底和柱墩底的最大彎矩基本處于1×103kN·m～1×104kN·m范圍內，而樁的彎矩則集中于10 kN·m～1 000 kN·m，以R 等于10 為例，柱墩底彎矩為0.3×104kN·m，土層分界處樁基彎矩為0.167×103 kN·m，二者彎矩相差十幾倍。相同R情況下，橋臺底和柱墩底的最大彎矩要大于基樁的彎矩，這主要是因為橋臺底和柱墩底的彎矩通過承臺傳至下部群樁。所以，相同彎矩下，橋臺底和柱墩底年平均超越概率要更大。

5 結論

本文基于性態設計方法的基礎上，考慮變量的兩類不確定性，推導了地震危險性曲線、地震需求模型和性態指標危險性曲線，主要結論與認識如下：

（1）基于已建立的多跨樁基橋梁結構體系，擬合得到不同性態指標的地震需求模型和地震危險性曲線，表明采用PGV/PGA作為地震動強度指標可以很好地擬合性態指標，表現出較好的相關性。

（2）基于不同性態指標的地震需求模型，得到體系最大彎矩和最大位移與最大PGV/PGA 并不完全對應。相同PGV/PGA情況下，承臺、橋臺和柱墩的最大位移要大于樁的最大位移，橋臺底和柱墩底的最大彎矩要大于基樁的最大彎矩。

（3）地震危險性曲線本質上是整個結構抗震性能的概率模擬，可以定性得到不同響應量達到或超越某種破壞狀態時的年平均超越概率。