不同洞口位置節能砌塊隱形密框復合墻體恢復力模型研究

倪博文，李升才，朱永甫

（1.華僑大學土木工程學院，廈門 361021；2.閩南理工學院綠色建筑施工與管理福建省高校工程研究中心，泉州 362700）

引言

我國建筑行業正處于繁榮時期，國內目前正在大力推動綠色建筑的發展，綠色建筑在未來幾年將會以迅猛發展的勢態占據市場［1］。節能砌塊隱形密肋框架結構是以合理構造措施將鋼筋混凝土與輕質砌塊結合成具有良好抗震性能的結構，同時也是一種綠色環保的結構體系。該課題組研究的節能砌塊隱形密框復合墻體是為了應用于我國多層及中高層住宅建筑結構，該墻體由節能砌塊和隱形密肋框架組成，節能砌塊隱形密框復合墻體的保溫（隔熱）隔音效果優良、施工工藝更為簡便和使用的材料不會對環境造成負擔［2］。目前國內已有對節能砌塊隱形密框復合墻體的抗震性能進行研究，李升才等［3－5］對節能砌塊隱形密框復合墻體進行模擬地震振動臺試驗，研究發現節能砌塊隱形密框墻體頻率下降和周期的上升都比較緩慢，表現出良好的抗震性能，研究還發現開洞的節能砌塊隱形密框復合墻體會有更加良好抗震性能；黃端權等［6］對6片1/2 縮尺的開洞密框復合墻體進行擬靜力試驗，提出考慮墻體配筋率和開洞形式兩個參數的恢復力模型；LIN 等［7］對12 片節能砌塊隱形密框復合墻體在低周反復荷載下的試驗數據分析，考慮了軸壓比和剪跨比對恢復力模型的影響。以上研究雖然考慮了開洞口、軸壓比和剪跨比對各項抗震指標的影響，但并未考慮開洞口位置對墻體抗震性能的影響，因此本文在上述研究的基礎上研究考慮不同洞口位置對墻體滯回特性的影響。

恢復力模型是用于高層建筑結構抗震分析的有利工具，同時也是結構進行彈塑性動力分析和理論計算的重要基礎［8］。趙軍等［9］對5 個鋼纖維增強混凝土剪力墻在低周反復荷載下加載，基于試驗結果，提出了適合于鋼纖維增強混凝土剪力墻的恢復力計算模型，計算結果和試驗結果吻合較好；李曉蕾等［10］通過對12 個鋼筋混凝土短肢剪力墻試件的低周反復荷載試驗數據分析，建立考慮剛度退化的短肢剪力墻恢復力模型，結果較為精確且便于實際應用；王義俊等［11］通過對6 片內置暗支撐剪力墻在低周往復荷載作用試驗的基礎上，對試驗數據進行擬合分析，得出的恢復力模型擬合效果良好；李健等［12］基于8 個高強混凝土雙鋼板組合墻的試驗研究成果，得到高強混凝土雙鋼板組合墻骨架曲線的特征參數計算式，并對試驗結果進行回歸分析，得出的三折線恢復力模型與試驗曲線相對比，兩者的吻合程度較好。

本文基于6 個不同洞口位置節能砌塊隱形密框復合墻體試件在低周往復荷載作用下的試驗結果，通過對其骨架曲線和滯回性能進行分析，采用數據擬合、線性回歸和理論分析的方式，給出適用于不同洞口位置節能砌塊隱形密框復合墻體的四折線恢復力模型以及各特征點的計算表達式，以期為此類構件的工程應用提供參考。

1 試驗概況

1.1 試件設計

該試驗以6 個帶門洞口的1/2 比例縮尺模型為研究對象，主要參數為洞口位置的改變。復合墻體由頂梁、地梁、節能砌塊和隱形密肋框架（肋梁肋柱組成密肋框架）構成，各墻體的長度、高寬和厚度均保持不變，分別為2 700 mm、1 350 mm 和110 mm，洞口的長度和高度分別是600 mm 和1 050 mm。試件MEW1～6 的門洞中線距墻體對稱軸的水平距離分別為750 mm、600 mm、450 mm、300 mm、150 mm 和0 mm，保持門洞尺寸不變，具體試件尺寸及構造信息見圖1 及表1。節能砌塊采用石膏材料制成，其長、寬和厚分別為150 mm、150 mm和110 mm，為了方便圓形密肋柱和矩形密肋梁的澆筑，在砌塊的上部和兩端分別留置60 mm×50 mm的矩形凹槽和直徑60 mm的半圓形缺口。

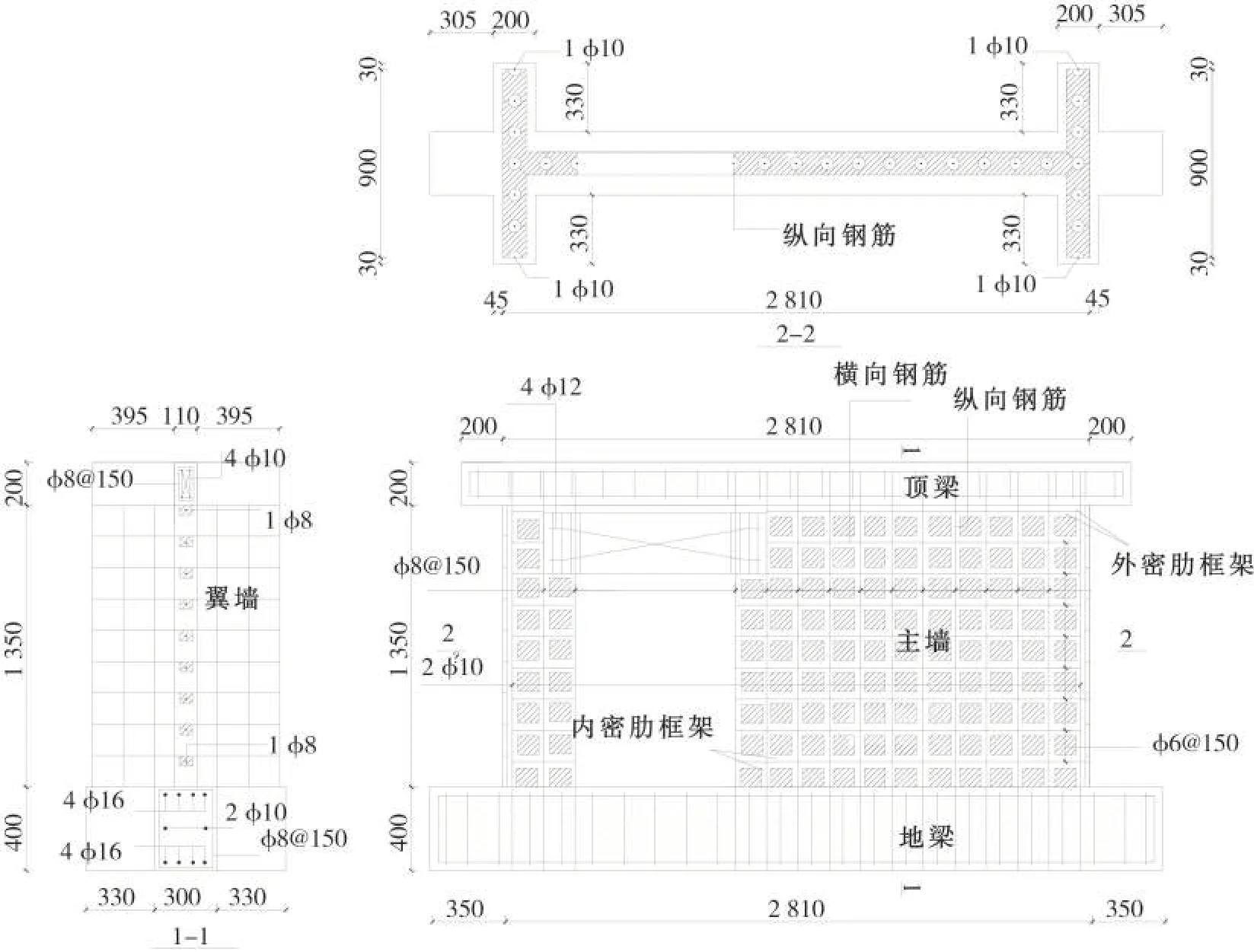
圖1 MEW1模型試件配筋圖Fig.1 Reinforcement drawing of MEW1 model specimen

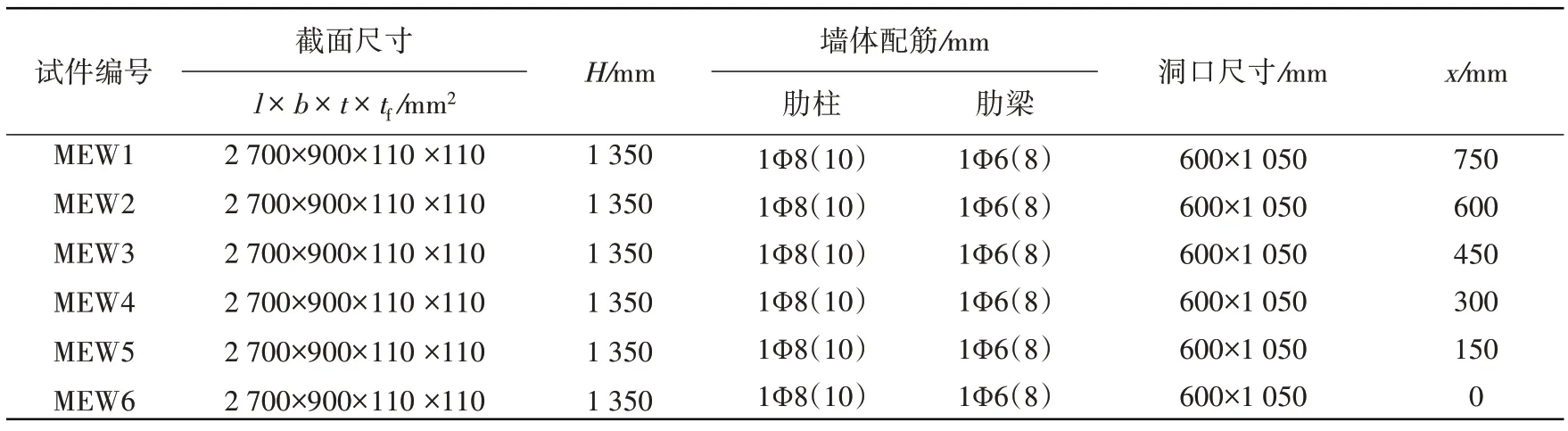
表1 試件基本參數Table 1 Basic parameters of specimen

1.2 材料力學性能

試件的注漿材料使用C20密實混凝土，其力學性能見表2，試件中主墻的鋼筋統一使HPB300，其力學性能經試驗測得的結果見表3。實測石膏砌塊的抗壓強度為15.8 MPa和抗拉強度為1.6 MPa，砌塊的干容重和彈性模量分別是10.15 kN/m3和1 950 MPa。

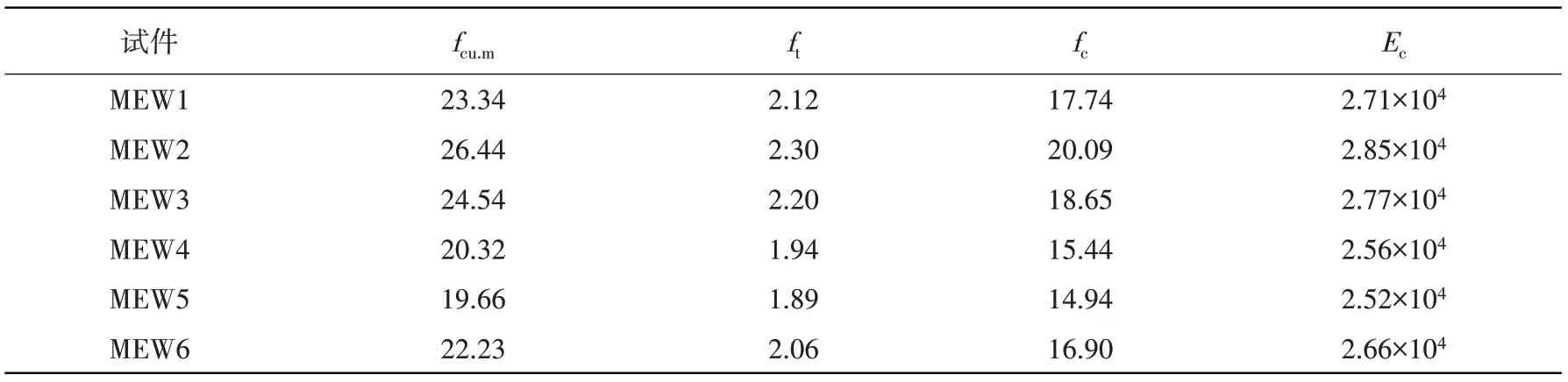
表2 注漿材料材性試驗結果Table 2 Test results of grouting material properties MPa

表3 鋼筋材性試驗結果Table 3 Test results of steel bar properties

1.3 試驗加載方案

該次試驗使用MTS 電液伺服加載系統對復合墻體進行低周往復水平加載，如圖2 所示。將地梁固定在實驗室的地面上，兩邊采用水平千斤頂頂緊，水平載荷通過液壓伺服載荷系統周期性的施加在頂梁中心，加載制度根據《建筑抗震試驗方法規程》（JGJ/T-2015）［15］的規定進行設計，具體加載制度見表4。在加載的初始階段，試件每級加載位移正反只進行一次，在試件屈服后，試件每級加載位移正反進行兩次，當水平承載力下降到峰值荷載的85%以下或墻體發生破壞時，停止試件加載。

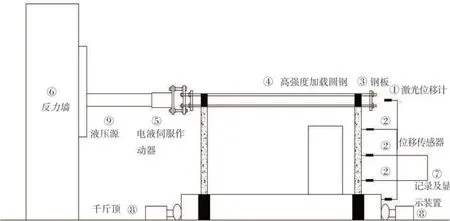
圖2 加載裝置Fig.2 Test setup

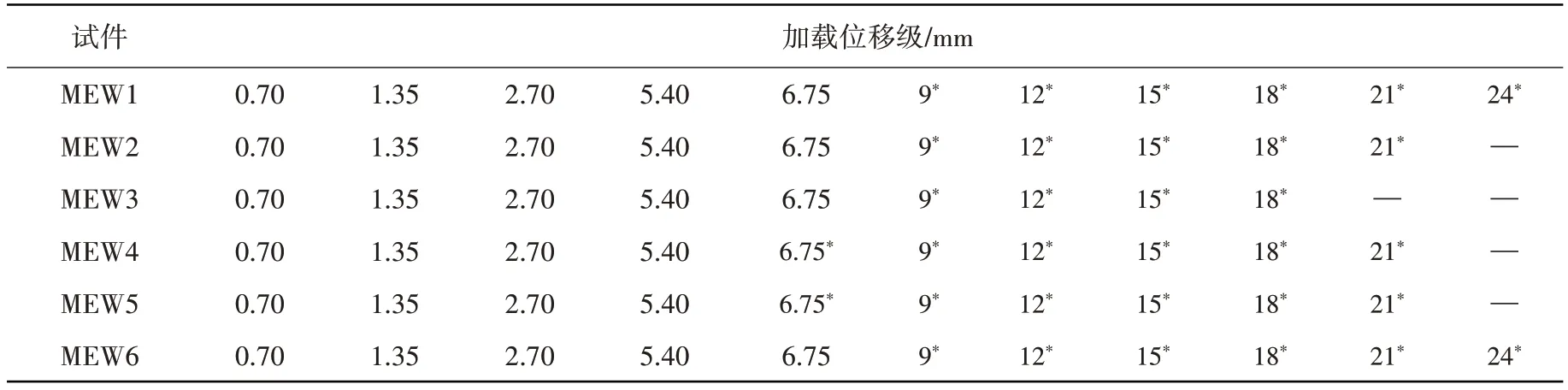
表4 試件的加載制度Table 4 Loading process of specimens

1.4 試件的破壞過程

復合墻體在試驗中的破壞模式可歸納為兩類：第一類是剪壓破壞，主要有試件MEW1、MEW2、MEW3和MEW6；第二類是水平剪切滑移破壞，有MEW4和MEW5兩個試件。試件MEW4和MEW5是由于頂梁下的兩個砌塊未能與下方的砌塊同時砌筑，從而留下了施工縫，這也造成了兩個試件發生了承載力下降嚴重的水平滑移破壞，如圖3 所示。試件MEW1、MEW2、MEW3 和MEW6 在砌筑過程中未出現較大的問題，最后的破壞形態都是較為理想的剪壓破壞。

圖3 水平施工縫Fig.3 Horizontal construction joint

復合墻體的剪切破壞現象以試件MEW1 為例，具體的破壞過程如下：水平力正向加載到62 kN 左右，可觀察到試件上有裂縫出現，但裂縫寬度較小，反向加載到118 kN左右，密肋梁與密肋柱內的部分鋼筋發生屈服，試件上的裂縫發生交叉，當加載至極限荷載165 kN 時，此時墻體承受的荷載開始降低，復合墻體中配置的鋼筋發生屈服，當荷載下降至極限荷載的85%附近，可以觀察到墻體內鋼筋破壞情況，停止加載，圖4為墻體的最終破壞形態。

圖4 試件的剪壓破壞形態Fig.4 Failure modes of specimens under shear compression

復合墻體的水平剪切滑移破壞先以試件MEW5為例，具體的破壞過程如下：當水平力正向加載至41 kN左右，墻體中間左側的砌塊出現首條斜裂縫，反向加載到110 kN 左右，原有的裂縫擴展延伸，裂縫數量開始大量增加，墻體內已有大部分的鋼筋開始屈服，當加載至極限荷載115 kN，原有的豎向裂縫逐漸發展為較寬的通縫。墻體左側有一部分砌塊鼓出和剝落，墻體內部分密肋梁與密肋柱內的鋼筋明顯屈服。當荷載下降至極限荷載的85%以下時，墻體中間部位有著較長的水平貫通裂縫，出現水平剪切滑移破壞，停止加載，圖5為墻體的最終破壞形態。

圖5 試件的水平剪切滑移破壞形態Fig.5 Failure modes of horizontal shear slip of specimens

1.5 試件的破壞機理

復合墻體發生剪壓破壞是一種理想的破壞狀態，破壞過程可分為三個階段。墻體在彈性階段，砌塊開始出現微裂縫，密肋框架未發現裂縫，其剛度基本不變，試件的殘余變形很小；在彈塑性階段，因為部分砌塊開始剝落且肋梁肋柱出現少量的微裂縫，試件的剛度有著些許的退化，內置鋼筋在循環荷載下開始成為主要受力構件，塑性變形有所發展，墻體耗能加快，進入破壞階段，砌塊開始出現嚴重的開裂和剝落，內密肋框架整體發生較大的變形，剛度明顯退化。

復合墻體在發生水平剪切滑移破壞時，破壞過程同樣可分為三個階段，墻體在彈性階段，砌塊同樣開始出現微裂縫，剛度并未發生變化，在彈塑性階段，墻體內大部分鋼筋開始屈服，內密肋框架出現彎曲，此階段破壞模式與剪切破壞較為相似，但墻體施工階段由于砌塊之間不緊密存在較大的施工縫，所以試件整體剛度和承載力都較低，到達破壞階段，密肋梁與密肋柱內的鋼筋明顯屈服，墻體砌塊出現大面積的破壞，水平縫貫穿成一條通縫，墻體被剪切分層，上下層間滑移嚴重，剛度發生明顯的下降。

1.6 滯回曲線

滯回曲線是進行非線性分析和確定恢復力模型的重要依據［16］，試件在水平低周往復荷載下的受力性能可以用滯回曲線描述。圖6 為6 個不同洞口位置節能砌塊隱形密框復合墻體的滯回曲線，為研究其滯回特性，對其進行展開分析，具體如下：

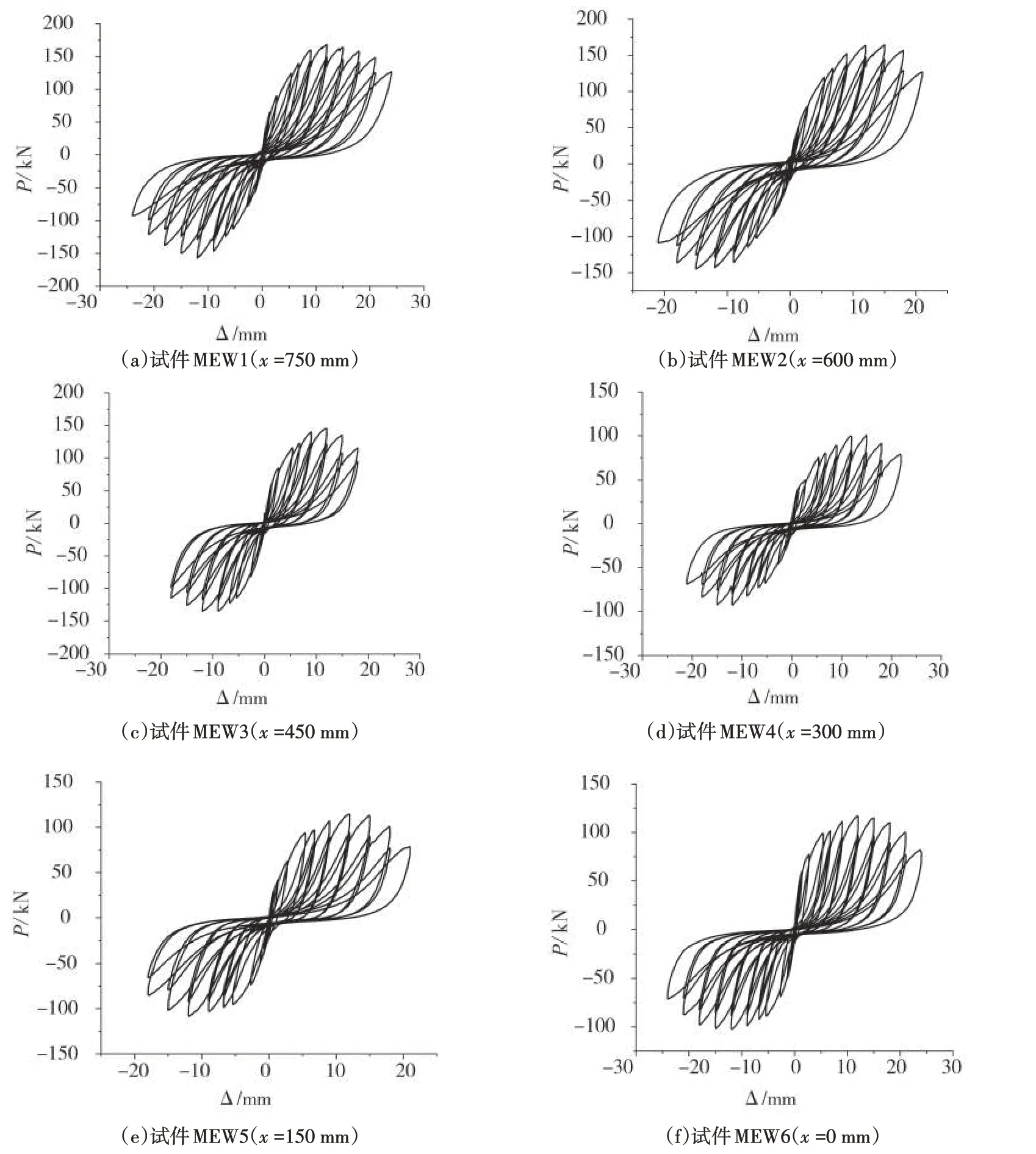
圖6 墻體的滯回曲線Fig.6 Hysteresis curve of walls

（1）試件從彈性階段進入強化階段的應力-應變曲線均較為平滑，未見明顯的屈服點。滯回曲線的形狀隨著荷載的增大發生一定程度的捏攏，同時力和位移的關系開始呈非線性關系。試件在到達屈服荷載后，隨著加載的進行，墻體的剛度發生了明顯的退化，在原點附近的滯回曲線發生了更為嚴重的捏攏。

（2）試件MEW6在到達峰值荷載前，剛度下降的速度最快，而MEW1的剛度下降速度最慢。試件MEW2和MEW1在加載至最大荷載之后，其荷載下降速度與其他試件相比較快，試件MEW6的荷載下降速度較慢，這體現出墻體洞口位置是影響滯回曲線的重要因素。

（3）綜上所述，所有墻體的滯回曲線形狀較為飽滿，條件相同的情況下，洞口位置位于墻體中部時，墻體的承載力較低，但墻體的耗能能力比洞口靠近邊緣的墻體更好。

1.7 骨架曲線

整理6個復合墻體試件的數據，將各個試件的骨架曲線列于圖7中，從骨架曲線中可以看出墻體的受力過程可大致劃分為以下四個階段，分別是彈性階段、屈服階段、強化段和強度退化段。

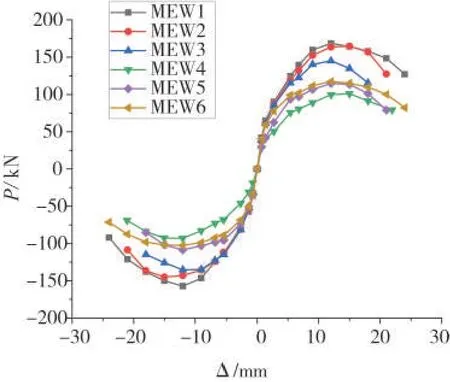
圖7 墻體的骨架曲線Fig.7 Skeleton curve of walls

彈性段大致為試件開始加載至開裂荷載，骨架曲線表現出較為明顯的線性關系，基本為一條直線，墻體在加載至屈服荷載前，雖然承載力依舊繼續上升，但試件剛度在逐漸降低，力和位移開始呈非線性變化，故可視為到達屈服階段；從試件屈服點到試件峰值點的過程可視為強化段，該階段荷載隨位移增加的速度開始放緩，出現較為明顯的剛度退化；試件達到峰值荷載后，骨架曲線下降段逐漸平緩，表現出了墻體有著較好的延性；墻體的抗剪承載力在加載至破壞荷載后開始迅速降低，變形也快速增大，此時墻體的穩定性較差。可以看出洞口位置越靠近墻體邊緣，墻體的承載力在增加，但曲線的下降段的斜率也越大；骨架曲線在正向加載時位移與荷載所體現出的變化趨勢和反向是基本相同的。

綜上所述，骨架曲線在彈性階段、屈服階段、強化段和強度退化段表現出的力學特征，基本可以反映6個

墻體在低周往復加載時的受力過程。洞口位置對滯回曲線有著明顯的影響，為了使骨架曲線模型的結果更加準確可靠，應當要考慮此種影響。

2 建議的恢復力模型

2.1 建議的骨架曲線模型

通過對6 個復合墻體的試驗結果進行研究，分析相關試驗現象、滯回曲線及骨架曲線，并結合前人的研究方法［17－18］，采用四折線模型作為不同洞口位置節能砌塊隱形密框復合墻體簡化后的骨架曲線，如圖8所示。

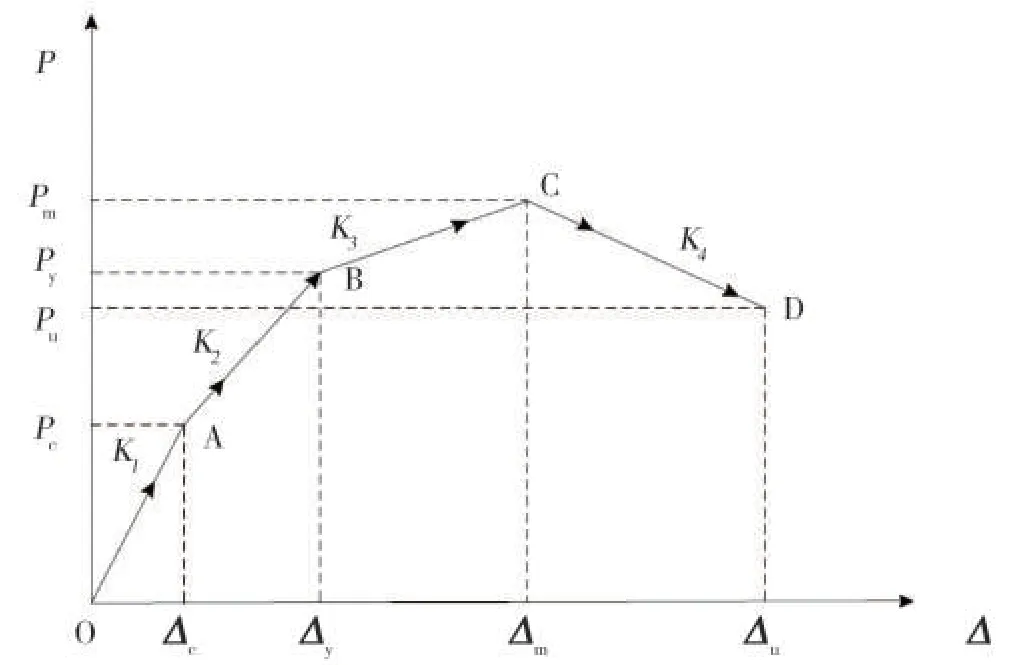
圖8 簡化骨架曲線Fig.8 Simplified skeleton curve

（1）彈性階段（OA段）

該試驗以骨架曲線出現首個明顯的轉折點作為開裂點A，OA 段表示的是試件的彈性階段，K1是其試驗彈性剛度，其計算公式為：

式中：Δc為墻體的開裂位移；Pc為墻體的開裂荷載。

（2）屈服階段（AB段）

試件屈服后，在往復荷載作用下，墻體的的變形不斷增加，K2是墻體進入彈塑性階段時的屈服前的試驗剛度，其計算公式為：

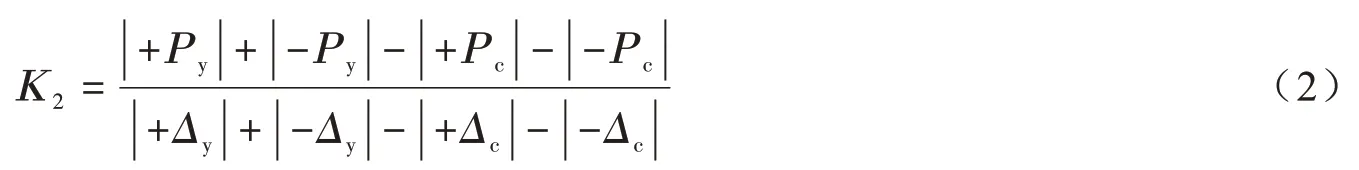
式中：Δy為墻體屈服位移；Py為墻體屈服荷載。

（3）強化段（BC段）

荷載達到峰值后，墻體新裂縫出現的數量開始減少，K3是墻體從屈服到最大荷載時的屈服后的試驗剛度，其計算公式如下所示：

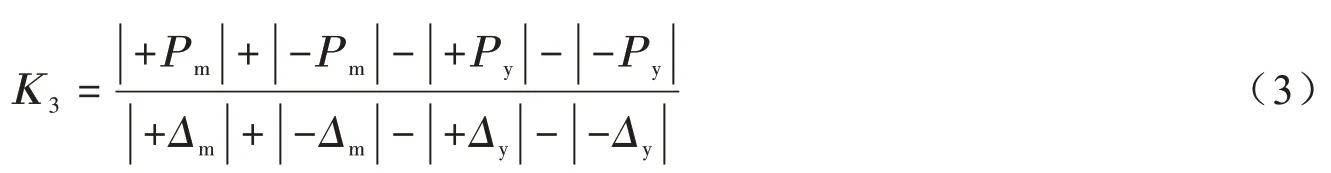
式中：Pm為墻體峰值荷載；Δm為墻體峰值荷載對應的位移。

（3）強度退化段（CD段）

強度退化段為圖中骨架曲線峰值點與極限點連線的直線段，K4是墻體從最大荷載狀態到極限位移狀態時的試驗剛度，其計算公式為：

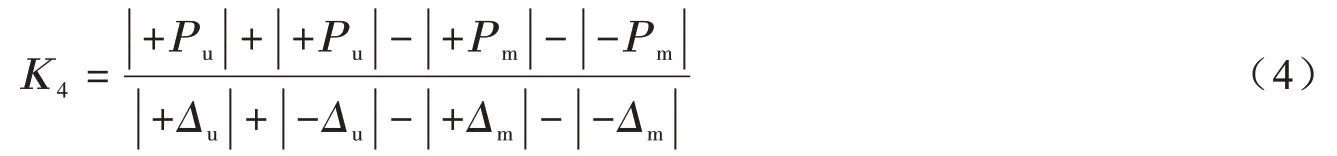
式中：Δm為墻體的極限位移；Pu為墻體的極限荷載。

墻體在各階段的試驗剛度值見表5。

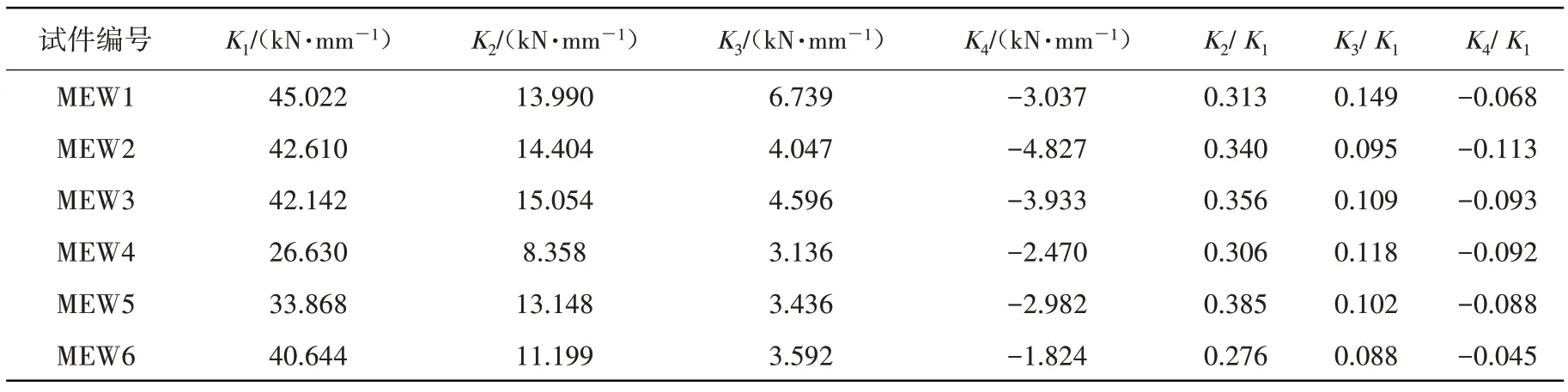
表5 試驗剛度值Table 5 Test stiffness value

2.2 骨架曲線特征值計算

2.2.1 特征剛度計算

根據已有對開洞復合墻體的試驗研究［19］，不同洞口位置墻體的彈性抗側剛度可以用式5 計算，但文獻［19］給出的計算公式存在量綱問題，式中：a應為無量綱量，反映了洞口位置對試件承載力的影響，故對a進行修正，令a=x/l。

式中：S1為洞口水平位置影響系數，S1=1.458a2+0.184 6；S2為開洞率η影響系數，S2=0.097η+0.128，η=，Am為墻體的孔洞面積，An為墻體的全面積；，其中：A為墻體的橫截面面積；μ為剪力分布不均勻系數；E為墻體的彈性模量；G為墻體的剪切模量。

表6 為彈性段計算剛度值與試驗剛度值對比。從表6 中可以看出式（5）計算出的彈性抗側剛度和試驗值有一定的誤差，故考慮對初始剛度K0進行修正，修正后的公式如式（6）和式（7）所示，修正后的彈性抗側剛度計算結果列于表6中，MEW4試件在制作過程中出現振搗不密實以及施工操作不規范，導致墻體內部存在初始裂縫以致于試件的剛度出現了非常嚴重的偏離；而其他試件的計算彈性剛度與試驗剛度的誤差值都能達到10%以內；MEW6 試件的誤差較大，達到10%；MEW2 試件僅有1%的誤差；除去MEW4 試件，其他試件的平均誤差在5.6%左右。

表6 彈性段計算剛度值與試驗剛度值對比Table 6 Comparison of elastic stiffness calculated values and tested values

對于四折線骨架曲線的K2、K3和K4階段的加載剛度采用如下方式進行確定：

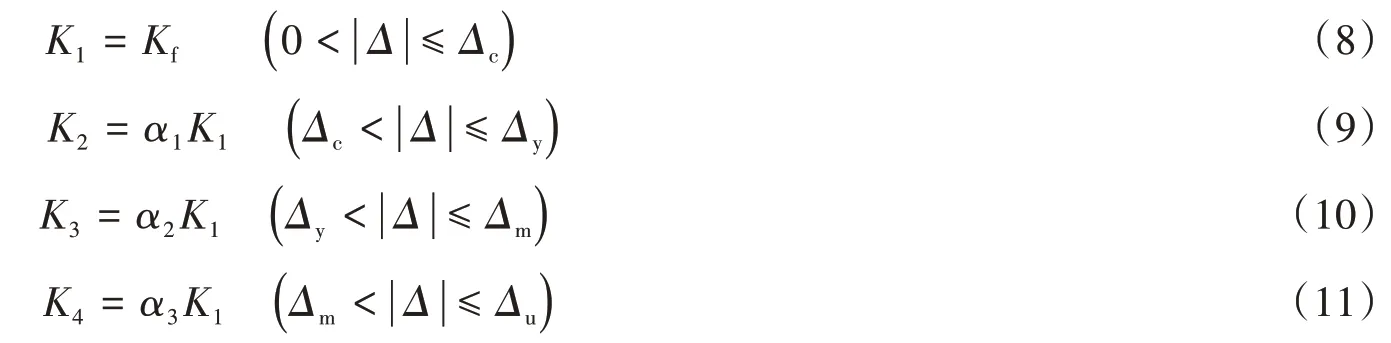
式中：α1、α2和α3是試驗回歸系數，利用最小二乘法對表5和表6中的數據進行回歸分析取α1=0.295、α2=0.26和α3=-0.122，α1、α2和α3的相關系數分別為0.53、0.88、和0.51，可見三個系數具有較高的擬合精度。

2.2.2 特征荷載值計算

通過查閱相關文獻［20］，已有的不同洞口位置隱形密框復合墻體斜截面抗剪承載力計算公式與本文的荷載試驗值有一定的誤差，通過與試驗數據的對比，對文獻［20］的公式進行修正，如式（12）所示。

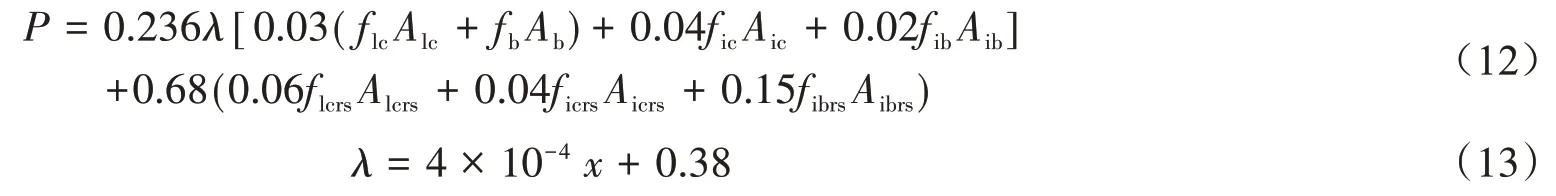
式中：P為墻體計算抗剪承載力；λ為綜合考慮洞口水平位置與開洞率影響系數；Alc為邊肋柱截面面積；Aic為內肋柱截面面積；Aib為內肋梁截面面積；Ab為砌塊截面面積；Alcrs為邊肋柱鋼筋截面面積；Aicrs為內肋柱截面面積；Aibrs為內肋梁鋼筋截面面積；flc為邊肋柱灌漿料抗壓強度設計值；fic為內肋柱灌漿料抗壓強度設計值；fib為內肋梁灌漿料抗壓強度設計值；fb為砌塊抗壓強度設計值；flcrs為邊肋柱鋼筋的抗拉強度設計值；ficrs為內肋柱鋼筋的抗拉強度設計值；fibrs為內肋梁鋼筋的抗拉強度設計值。

根據式（12）計算墻體抗剪承載力理論計算值。

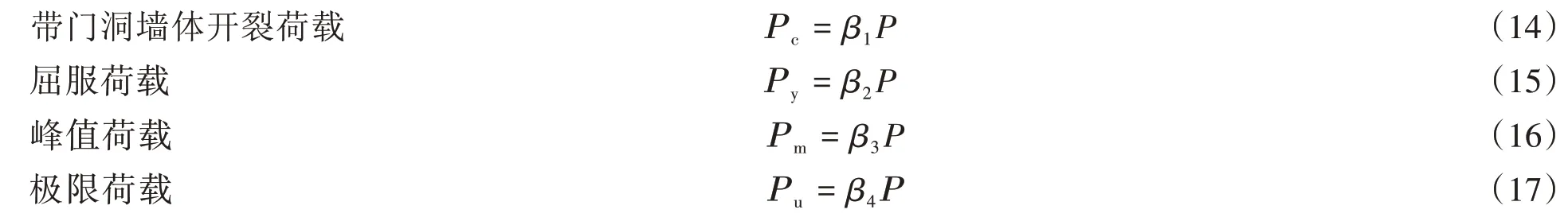
式中：β1、β2、β3和β4是利用最小二乘法得到試驗回歸系數，β1=0.284、β2=0.713、β3=1、β4=0.850，β1、β2、β3和β4的相關系數分別為0.824、0.997、1 和1，通過以上公式求出6 個試件的計算特征點，并與試驗特征點比較，如圖9所示。

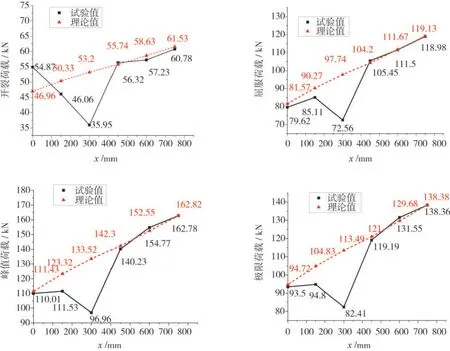
圖9 計算荷載與試驗荷載值對比Fig.9 Comparison of load calculation value and load test value

2.3 卸載剛度

墻體在屈服階段、峰值階段和破壞階段的卸載剛度可以利用線性插值法求出，圖10為節能砌塊隱形密框復合墻體的剛度退化規律。在試件開裂以前，試件處于彈性階段，卸載剛度可取開裂剛度；從屈服點開始卸載的剛度是Kr1；Kr2和Kr3則分別是峰值點和極限點的卸載剛度。

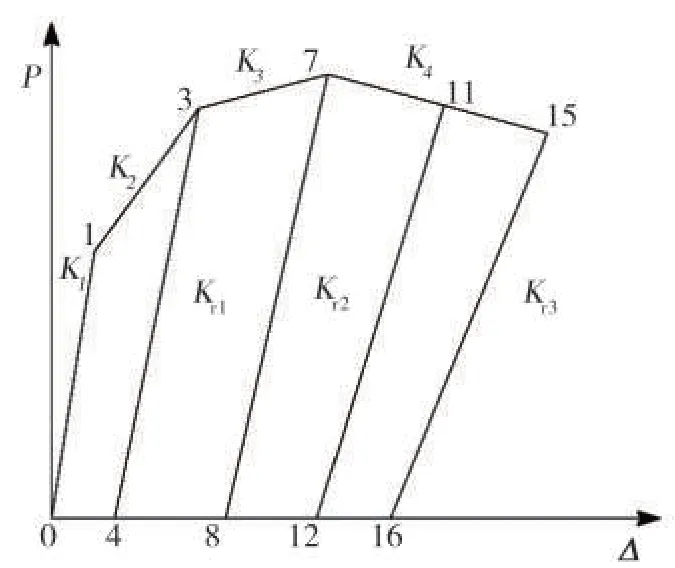
圖10 剛度退化規律Fig.10 Stiffness degradation law

經試驗回歸分析，建議如下卸載剛度計算公式：

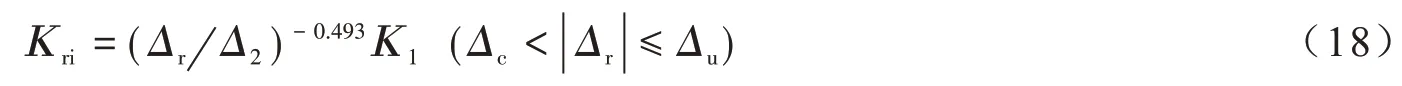
式中：Kri為墻體的卸載剛度；Δr為墻體卸載時的側向位移；Δ2為試件開裂時的加載位移。

2.4 滯回規則

節能砌塊隱形密框復合墻體的恢復力模型的滯回規則可在四折線骨架曲線模型的基礎上提出，具體規則如圖11所示。

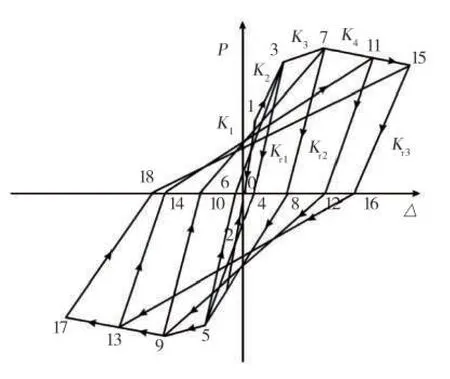
圖11 四折線型恢復力模型Fig.11 Four fold linear restoring force model

（1）在加載至開裂點1前，試件處于彈性階段，加載和卸載路徑沿著?→①→?→②→?，加載和卸載剛度均為初始彈性剛度。

（2）屈服前滯回路徑為?→①→③→④→②→⑤→⑥→③，加載路徑沿著開裂點①至屈服點③，卸載路徑沿著③到④；卸載剛度可由式（16）獲得，反向加載時，加載路徑沿著②至屈服點⑤，接著反向卸載的路徑從屈服點⑤到點⑥，最后正向加載到點③。

（3）試件屈服后進入強化階段，此時試件在③→⑦直線段開始屈服，卸載時可觀察到剛度出現退化，卸載路徑沿著⑦→⑧直線，由式（16）可得到此時的卸載剛度；開始反向加載后，如果有試件的水平荷載超過屈服荷載，則此時路徑由正向卸載至荷載為零的點⑧，直接指向屈服點⑤，后沿著反向加載路徑⑤→⑨進行，到達位移幅值之后開始卸載，卸載剛度依舊由式（16）確定。

（4）再加載則由反向卸載至荷載零點，指向上一級位移幅值最大點（如⑩→⑦直線），之后沿著骨架曲線正向加載至本級最大位移點后卸載，卸載剛度按式（16）計算。反向加載與正向加載順序一致，由正向卸載荷載零點指向負向的上一級位移最大處（如⑧→⑨直線段），再沿著骨架曲線強化段負向加載至本級位移最大點處卸載。

（5）若上一級位移幅值等于或大于峰值荷載位移，則本次正向加載沿著骨架曲線下降段進行，滯回規則與強化段的規則相同。

2.5 骨架曲線比較

試驗所得的四折線骨架曲線與計算所得的四折線骨架曲線對比如圖12 所示。從圖12 中可以看出：MEW1、MEW2、MEW3和MEW6這4個試件的曲線對比吻合良好，而且精度較高。試件MEW4的曲線對比偏差較大，特征點的計算值要遠高于相應的試驗值，主要是由于墻體在在制作過程中出現振搗不密實以及施工操作不規范等現象；試件MEW5 的曲線對比在試件屈服前都有著較好的吻合，在試件屈服后骨架曲線對比存在一定程度的偏差特征點的計算值要稍高于相應的試驗值，主要是由于加載過程中儀器操作失誤而導致。但是整體上試件MEW4和MEW5的四折線骨架曲線模型發展規律與試驗結果相同。

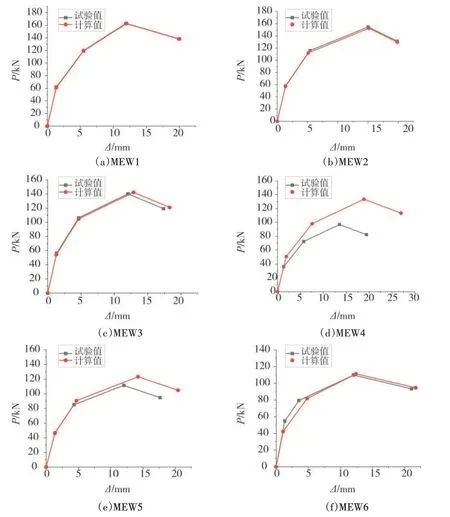
圖12 四折線骨架曲線對比Fig.12 Comparison of four fold line skeleton curves

3 結論

通過6個節能砌塊隱形密框復合墻體的試驗研究，分析試件破壞過程和滯回特性，對建立的四線型恢復力模型進行詳細闡述，最終得出如下結論：

（1）試件MEW1、MEW2、MEW3和MEW6出現剪壓破壞。另外，MEW4和MEW5兩個試件將會發生水平剪切滑移破壞。

（2）墻體在擬靜力試驗中，分別經歷了彈性、彈塑性和破壞三個階段，墻體滯回曲線形狀較為飽滿，表明結構有著良好的抗震性能；墻體的洞口位置位于中間時，骨架曲線下降段更為平緩，墻體的變形能力及延性要好于偏開洞墻體。

（3）提出骨架曲線各特征點的計算方法，將特征值點的計算值和試驗值進行對比，吻合較好，精度較高。

（4）通過四折線的恢復力模型得到的計算骨架曲線與試驗骨架曲線吻合度較高，可為隱形密框復合墻體彈塑性動力反映分析提供參考依據。