不對稱參數同塔四回線行波測距
于仲安,丁雯蘇,陳璐,畢俊強
(江西理工大學 電氣工程與自動化學院,江西 贛州 341000)
0 引 言
同塔四回輸電線路在緩解輸電走廊緊張,提高輸送容量方面具有明顯優勢,是實現高效輸電的一種有效手段。然而,架設線路的增加使得各回線之間耦合更加復雜,故障類型繁多,故障定位更加困難[1-2]。
當前,對于同塔四回線的故障測距研究多是基于穩態量的故障分析法[3-8],較難保證測距精度。行波測距精度高,是基于行波理論實現的測距方法,但主要針對單回線和雙回線[9-15]的故障測距。文獻[16-17]雖對同塔四回線的行波測距進行了分析研究,但其僅局限于對稱參數線路。實際上,由于空間距離、導線材料等差異,線路參數存在一定的不對稱性[18]。為此,目前尚未有對符合工程實際的不對稱參數同塔四回線進行行波測距的研究。
對于不對稱參數同塔四回線,由于線路間耦合復雜,因此合理的相模變換是其進行行波測距的基礎。另外,在四回線解耦后,由于各模量在不同故障類型下傳輸特性不同,選取何種模量進行測距,又是行波測距的關鍵問題之一。基于以上分析,文中通過深入分析不對稱參數同塔四回線的線路模型,從三種不同物理意義的角度介紹了相應的相模變換矩陣M1、M2、M3。對比分析三種解耦方式下各模量的相關特性,M1、M2解耦后的方案需在不同故障類型下選取不同的模分量來表征故障行波特征,較為復雜,不利于行波測距。而由M3解耦后的模量具有明顯的優勢,其解耦后的模2、模5、模8、模11與Ⅰ、Ⅱ、Ⅲ、Ⅳ回線一一對應,能夠將四回線下的行波測距轉換為單回線下的行波測距,極大地降低了由12模量傳輸特性不同所造成的選取何種模量進行行波測距的復雜度,巧妙地解決了故障行波選取的難題。最后通過3次B樣條小波包變換分析選取的模分量,依據雙端行波測距原理實現了不對稱參數同塔四回線的故障檢測與定位。大量的PSCAD/EMTDC暫態仿真實驗驗證了行波模量選取的準確性與行波測距的可行性。
1 相模變換
在不對稱參數同塔四回線系統中,行波在傳播時,由于四回線間存在復雜的電磁耦合,因此需要對四回線的阻抗進行合理的相模變換,繼而找到合適的模分量用于行波信號分析。
假設線路均勻換位,不對稱參數同塔四回線系統模型如圖1所示,圖2是相應的阻抗矩陣圖。
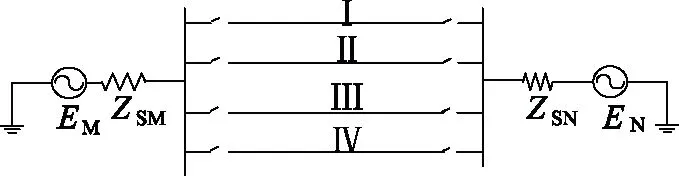
圖1 不對稱參數同塔四回線系統示意圖Fig.1 Schematic diagram of 4-parallel transmission
圖2中Zs1、Zm1分別為Ⅰ、Ⅱ回線的自阻抗與相間互阻抗。Zs2、Zm2分別為Ⅲ、Ⅳ回線的自阻抗與相間互阻抗。Ⅰ、Ⅱ回線和Ⅲ、Ⅳ回線線間阻抗分別為Zp1和Zp2。Ⅰ、Ⅲ回線和Ⅱ、Ⅳ回線線間阻抗均為Zq1。Ⅰ、Ⅳ回線和Ⅱ、Ⅲ回線線間阻抗均為Zq2。
由圖2可得如下電壓、電流矩陣關系:

圖2 不對稱參數同塔四回線阻抗矩陣圖Fig.2 Impedance matrix graph of 4-parallel transmission lines on the same tower with asymmetric parameters
(1)
式中Ui=(UiAUiBUiC)T;Ii=(IiAIiBIiC)T;i=Ⅰ、Ⅱ、Ⅲ、Ⅳ;
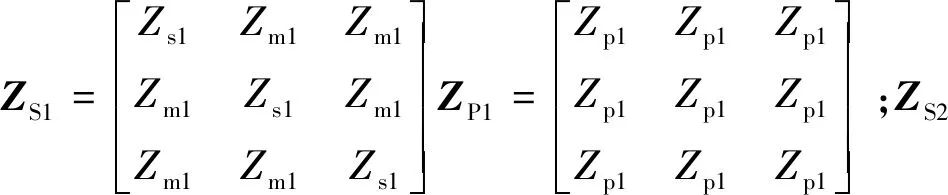
1.1 相模變換一
將四回線看成一個整體,通過引入不對稱參數K1,K2直接進行線間解耦,對于無法消除的單回線相間耦合,采用卡倫鮑爾變換,綜合步驟下的解耦矩陣M1為:
M1=
(2)
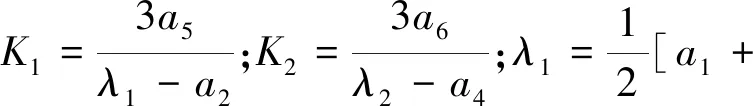
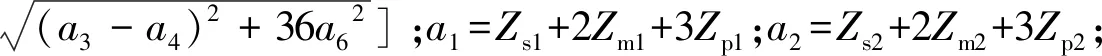
1.2 相模變換二
將圖1中的四回線看成兩組雙回線的并聯,為此先分別對Ⅰ、Ⅱ回線和Ⅲ、Ⅳ回線進行線間解耦,對于無法消除的單回線相間耦合,采用卡倫鮑爾變換。最后引入不對稱參數K3、K4、K5、K6完成最終解耦,總的相模變矩陣M2如下:
M2=
(3)
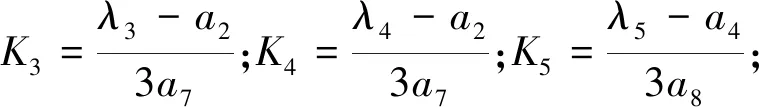
1.3 相模變換三
對于圖1中四回線也可以分別看成四個獨立線路,均采用文獻[19-21]中的新相模變換矩陣完成各單回線的解耦,實現正負序的完全獨立,同樣對無法消除的線間零序互感的耦合,通過引入不對稱參數K7,K8,K9,K10完成解耦,綜合步驟下的解耦矩陣M3為:
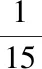
(4)
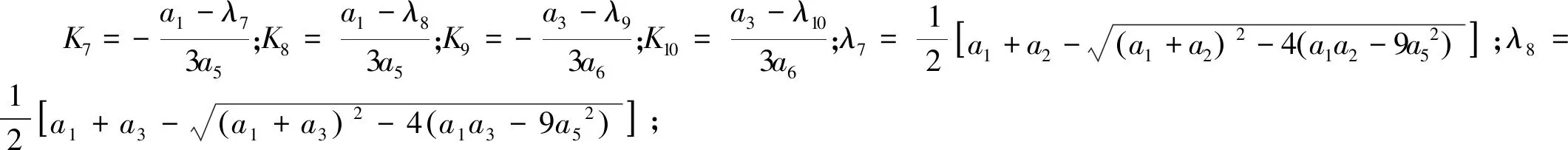
需要指出的是,以上三種相模變換均可適用于對稱參數同塔四回輸電線路的解耦。
2 故障模量行波的選取
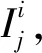
(5)
(6)
(7)
對比式(5)~式(7)中各模電流分量可知,當j=1、4、7、10時,三種相模變換下相對應的模電流均由不對稱系數Km(Km≠0,m=1~10)的線性組合構成,由于Km與具體的線路參數有關,計算復雜的同時無法確定相對應的模電流分量在十二相導線中的傳輸情況,故不宜作為故障測距的模量電流行波。
當j≠1、4、7、10時,為研究剩余模量的優異性,表1給出了由邊界條件求出的一些典型故障的模值。
由表1可知,M1、M2解耦的模分量與四回線對應較為復雜,不同故障類型下無統一的電流模值反映故障情況。為此當發生不同故障時,需要選取不同的電流模分量(不為0的模量)來表征故障行波特征,這將增加行波測距的復雜度。
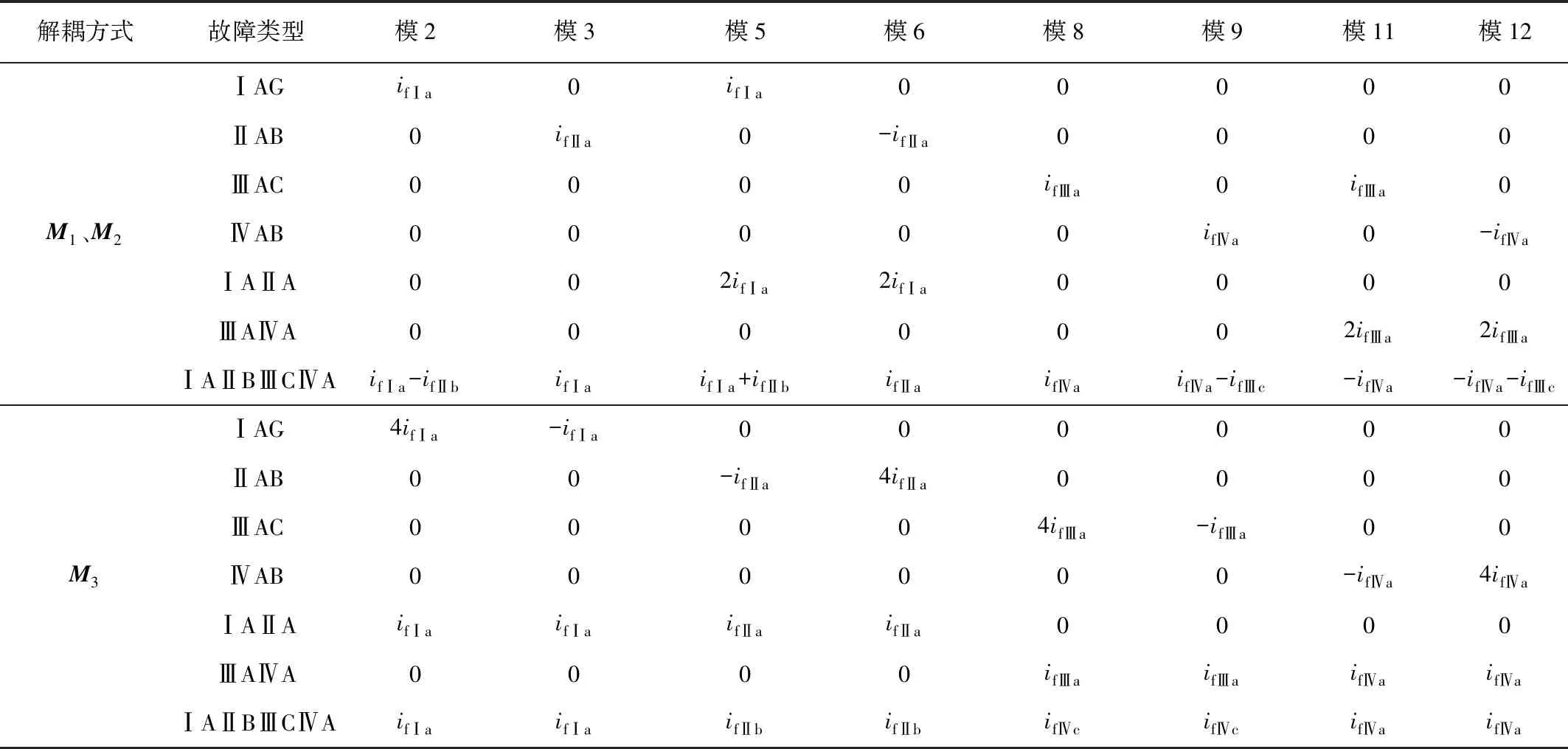
表1 三種解耦方式下不同故障類型的電流模值Tab.1 Current mode value of different fault types under three decoupling modes
而M3解耦后的模2(3)、模5(6)、模8(9)、模11(12)的值與各回線是否發生故障有著明顯的一一對應關系,有著獨特的自選線功能,即凡涉及I回線的各種故障(單回線或跨線故障),模2(3)不為0;涉及Ⅱ回線的模5(6)不為0;涉及Ⅲ回線的模8(9)不為0;涉及Ⅳ回線的模11(12)不為0。為此,這里選模2代表I回線,模5代表Ⅱ回線,模8代表Ⅲ回線,模11代表Ⅳ回線,通過四個模值是否為0的情況,可以判斷出故障類型,進而選出所用于行波測距的模量行波。例如,模2不為0,模5、模8、模11均為0,則表示僅I回線發生單回線故障,此時選取對應的模2分量為故障行波;當模2、模5不為0,模8、模11為0,則表示I、Ⅱ回線發生跨線故障,此時選取模2或模5作為故障行波,其他情況依此類推。
基于以上對比分析,三種物理意義下的相模變換中,第三種方案更加適用于行波測距。通過其解耦后的模2、模5、模8、模11四個模值為0的情況可以判別出單回線故障還是跨線故障,從而進一步選取相應的模分量作為故障行波,該優點極大地降低了不對稱參數同塔四回線因12模分量傳輸特性不同造成的測距行波選取的復雜度,巧妙地將四回線的故障行波測距轉化為單回線的行波測距。
3 故障測距方案
對于所獲取的模量行波,需要進行奇異點的檢測,準確定位行波到達點。小波包變換(WPT)能同時將高低頻再次進行分解,相比于小波變換其分析方法更為精細,時頻分辨更加明顯,故障檢測更加精準。在小波包變換中,對于小波函數的選取,3次B樣條小波包變換因其具有線性相位、最小支集和漸進最優,為此是理想的實現奇異信號檢測的小波函數,其滿足如下遞推關系:
(8)
式中μ(x)是B樣條小波函數;hk是低通濾波器;gk是高通濾波器。由于兩組濾波器的存在,使得3次B樣條小波包變換更加細致的刻畫出故障狀態不同尺度不同頻帶的時域特征,具體如圖3所示。
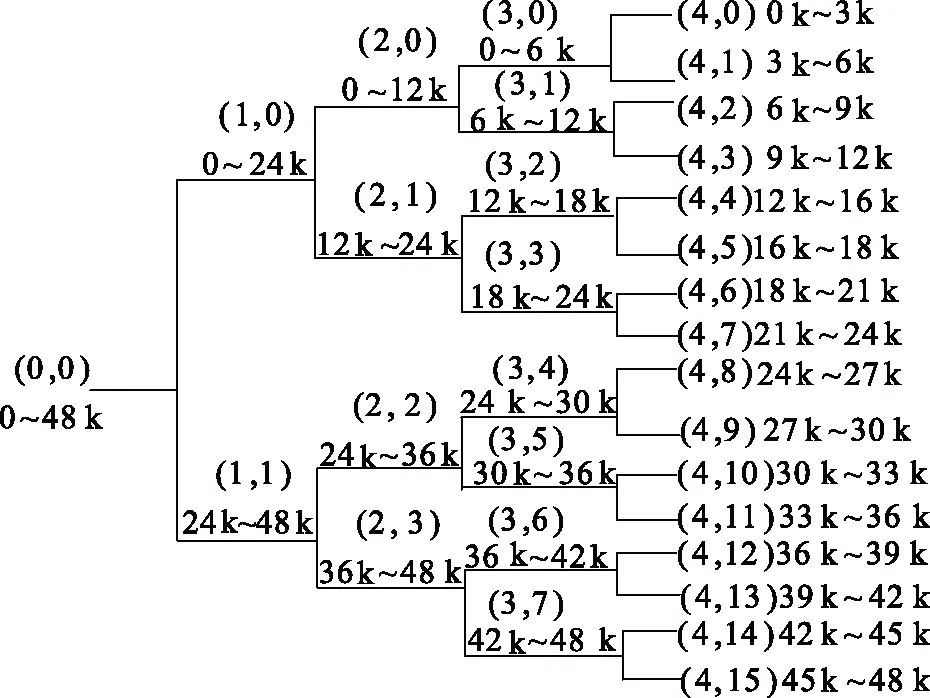
圖3 3次B樣條小波包變換的4層小波包分解樹Fig.3 4-layer wavelet packet decomposition tree under 3-time B-spline wavelet packet transform
采取3次B樣條小波包變換分解所得模量行波時,為降低干擾,應先比較低頻尺度下頻帶能量大小,選擇能量突變較大的頻帶尺度,在該尺度下找出模極大值出現的大致時間t,之后,為減少衰減,在所選尺度的較高頻帶下找出最靠近t的奇異點,此奇異點對應的時刻即為行波浪涌到達母線的時間。將檢測出的時間帶入雙端行波測距式(9),得最終的故障距離。
(9)
式中t1、t2表示行波浪涌到達母線M、N的時間;v為波速,這里取光速;L為故障線路總長。
基于以上分析,總的測距流程圖如圖4所示。
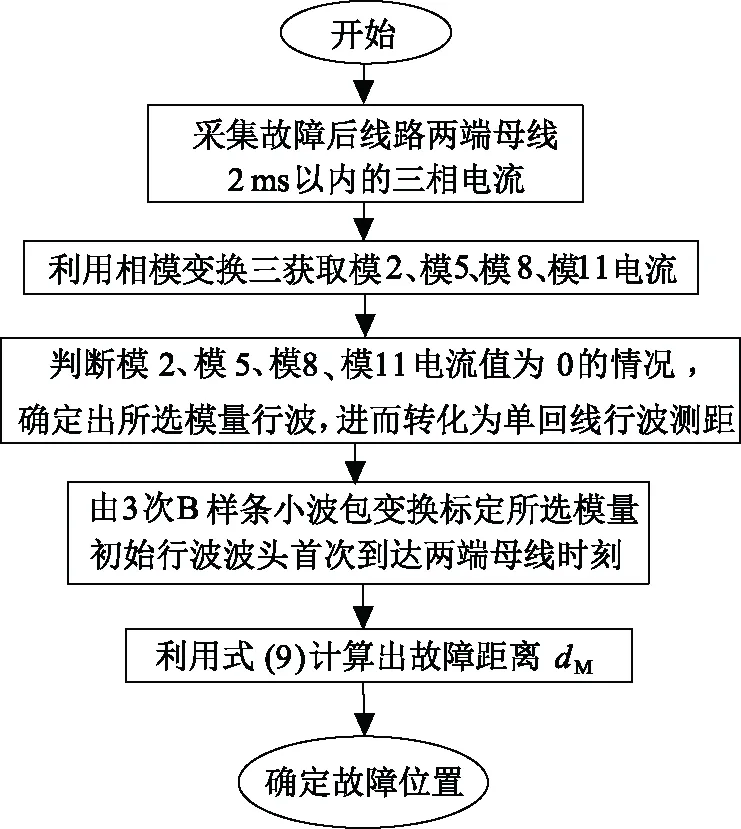
圖4 行波測距流程圖Fig.4 Flow chart of traveling wave fault location
4 仿真驗證
為了驗證相模變換的正確性與測距的可行性,以PSCAD/EMTDC搭建如圖1所示的仿真模型。塔型采用普遍使用的垂直分布塔型,線路全長300 km,雙端電源220 kV。M、N側系統正序阻抗均為j50 Ω,零序阻抗為j80 Ω。相關線路參數如表2所示。
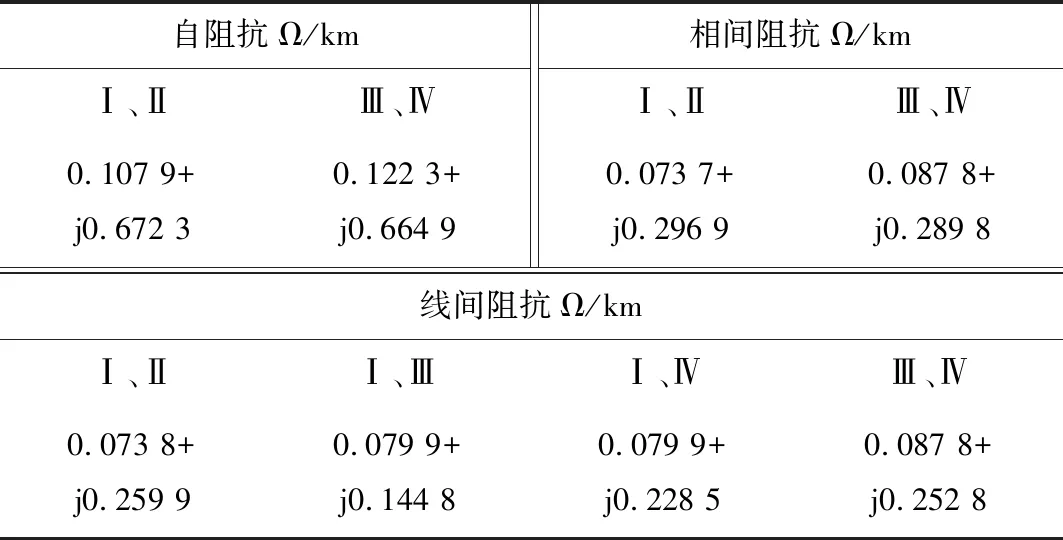
表2 不對稱參數的同塔四回線阻抗參數Tab.2 Impedance parameters of four-parallel transmission line on the same tower with asymmetric parameters
假設線路在0.01 s時距M側100 km處發生一回線A相接地故障,即ⅠAG故障,則測的M側模2、模5、模8、模11的電流經快速傅里葉變換下的幅值變化如圖5所示。
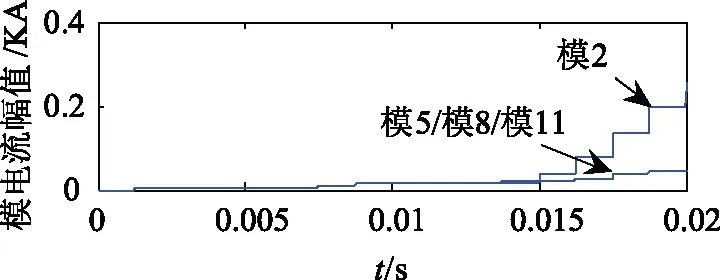
圖5 各模電流幅值Fig.5 Current amplitude of each mode
因同名相互感的影響,非故障相的A相電流增大,使得模5、模8、模11約等于0,但模2值遠大于模5、模8、模11,為此選取模2分量為故障行波。
取模2分量故障后2 ms內的暫態數據(下同),用4尺度的3次B樣條小波包進行變換,相應的變換結果如圖6所示。在4尺度的低頻帶中,第4尺度突變能量較大,因此選擇第4尺度為分析尺度,通過對第4尺度中高頻帶的分析,選取(4,14)頻帶為最終的故障定位頻段。由(4,14)中圖形可知,模極大值所對應的采樣點為212,經換算后t1=0.010 339 2 s。同理,按以上分析,N側變換結果如圖7所示。其中,模極大值對應的采樣點為421,經換算后t2=0.010 673 6 s。將t1、t2帶入式(9),求得dM=99.84 km,測距誤差為0.16 km,誤差在一個檔距之內,滿足測距精度要求。
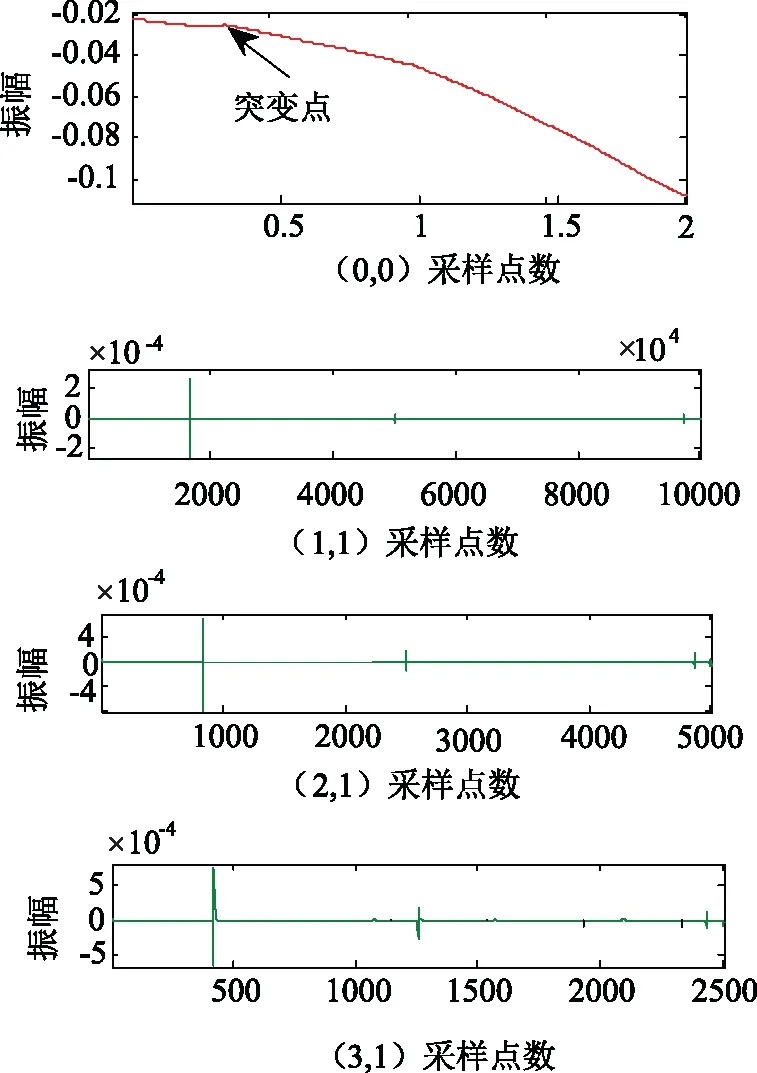
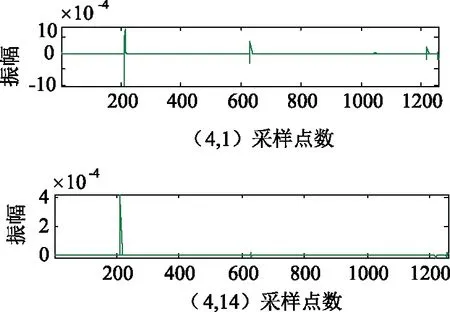
圖6 M端模2電流多尺度分析結果Fig.6 M-mode 2-current multi-scale analysis results
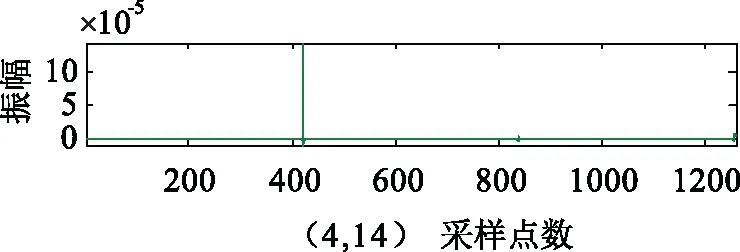
圖7 N端模2電流多尺度分析結果Fig. N-mode 2-current multi-scale analysis results
按照以上分析,表3、表4給出了部分故障類型和過渡電阻下故障點到M側的測距結果。
由表3、表4可知,在不同故障類型下,隨故障點的改變,測距結果仍滿足要求,且不受過渡電阻的影響,驗證了相模變換三下模量行波選取的準確性與不對稱參數同塔四回線行波測距的可行性。
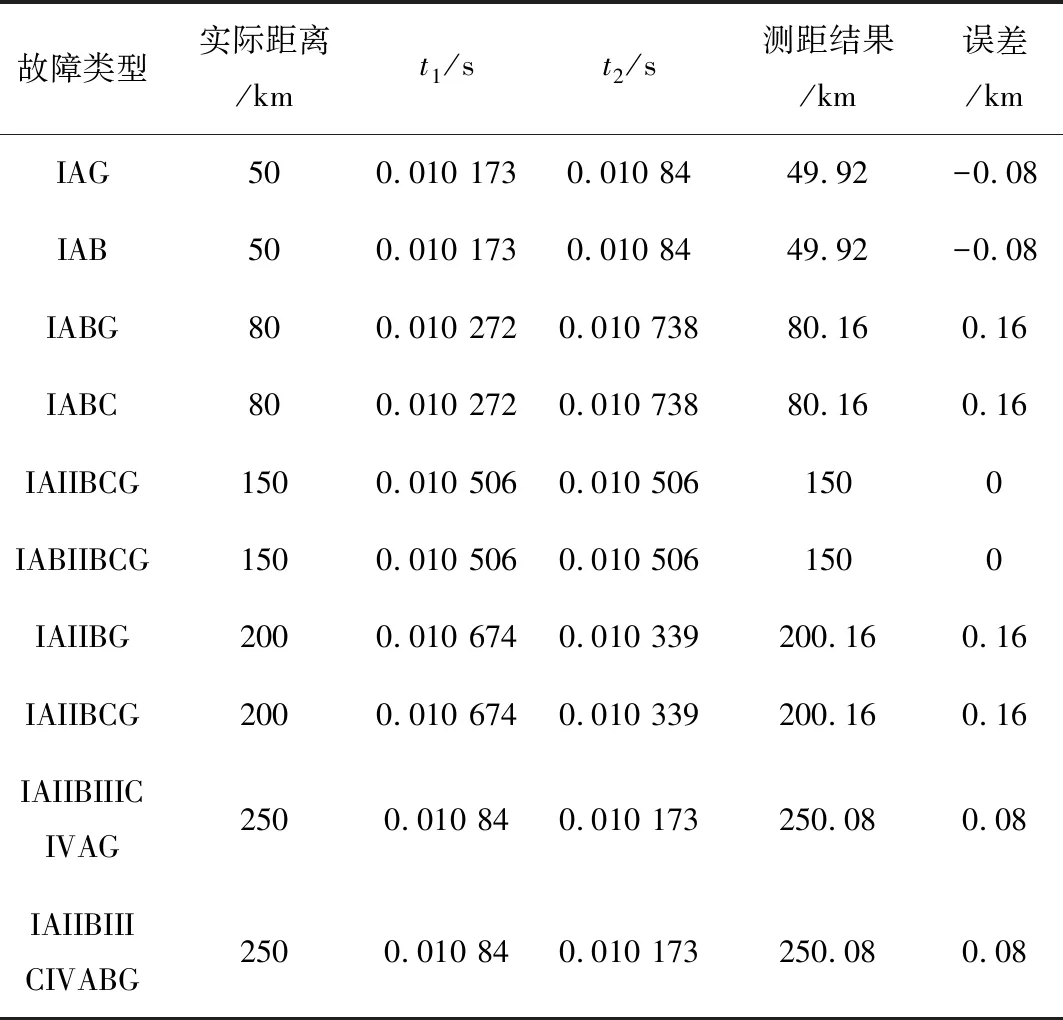
表3 不同故障類型下的行波測距結果Tab.3 Fault location results of traveling wave under different fault types

表4 不同過渡電阻下的測距結果Tab.4 Fault location results under different transition resistances
5 結束語
(1)通過搭建更貼合工程實際的不對稱參數同塔四回線模型進行理論分析,介紹了三種不同物理意義下的阻抗解耦矩陣M1、M2、M3;
(2)對比分析三種解耦方式下模分量的相關特性,找到了適合于四回線測距的模量行波。即由M3解耦后的模2、模5、模8、模11與Ⅰ、Ⅱ、Ⅲ、Ⅳ回線一一對應,具有自選線功能的同時能夠將四回線下的行波測距轉換為單回線下的行波測距;
(3)通過多尺度分析的3次B樣條小波包變換進行故障檢測,依據雙端行波測距方案進行故障測距。大量的PSCAD/EMTDC實驗仿真數據驗證了模量行波選取的準確性與不對稱參數同塔四回線行波測距的可行性;
(4)該方案同樣適用于對稱參數的同塔四回線,同時,也為下一步考慮波速變化以及弧垂影響等深入問題的算法優化奠定了基礎。

