基于改進遺傳算法的鐵路物流中心功能區布局優化研究

張 恒

(中國鐵路武漢局集團有限公司 計劃統計部，湖北 武漢 410073)

0 引言

近年來，隨著貨運需求的增加及市場競爭的加劇，鐵路物流基地和貨運場站作為鐵路貨運中心樞紐，是貨運至關重要的環節，其規劃和設計將影響整個鐵路貨運效率。針對鐵路物流中心規劃設計進行研究，對我國鐵路貨運適應現代物流的競爭環境并取得主導地位現實意義重大。由于貨物品類不同，且鐵路物流中心各功能區之間的貨運量存在差異，功能區之間的相關性各有不同。另外，加上物流中心的客觀限制條件，使得鐵路物流中心功能區布局優化成為一個NP 難問題。

目前我國關于物流中心的研究多集中于物流中心運營模式理論[1]、單一物流中心選址[2]及傳統貨運站向現代物流中心轉化的定性分析[3-4]等方面。求解鐵路物流中心功能區布局問題的方法主要有數學模型法[5-6]、系統布置規劃法(Systematic Layout Planning，SLP)[7]及計算機仿真等。近年來，從定性和定量2方面考慮的SLP 方法應用較多，采用的算法主要有啟發式算法、智能算法、計算機仿真方法等，其中智能算法被廣泛采用，包括遺傳算法、模擬退火算法、蟻群算法等。針對鐵路物流中心功能區布局優化模型，馮芬玲等[7]設計遺傳算法進行求解，通過對中心點位置和擺放方式進行編碼，將約束條件作為懲罰加入適應度函數；由于各功能區域相互位置的約束，造成該種方法無法保證解的可行性，容易產生不可行解；同時搜索空間過大，不易搜索到優解。谷樂陽[8]采用嚴格分層布局的方式進行求解，保證解的可行性，然而這種方法大大縮小了解的搜索空間，存在忽略相對優解的情況。

通過對鐵路物流中心功能區布局優化模型求解算法研究，提出一種高效遺傳算法。采用改進分層思想，通過從左到右、從下往上的緊密堆積布局方式，同時對各功能區域豎直采用連續上下位移選擇，優化物流區域布局。對編碼方式進行改進，針對功能區域布局順序、堆積方式和擺放方式，分別采用自然整數編碼、離散二進制編碼和連續區間的二進制編碼方式進行編碼，并進行遺傳操作，搜索區域布局優化解。通過算例比較，體現了改進遺傳算法的優越性。算法在保證解可行的前提下，擴大了搜索范圍，提高解質量，從而能夠獲得更優的鐵路物流中心功能區布局方案，為鐵路物流中心功能區布局提供技術支撐。

1 鐵路物流中心功能區布局優化模型

鐵路物流中心主要通過鐵路聯絡線以鐵路運輸方式進行物流活動，包括貨物承運、配送、儲存、運輸和交付等，按其作業流程及各項作業特點劃分為基本功能、增長功能和輔助功能3 大類12 個功能區。基本功能區包括：理貨區、流通加工區、倉儲區。增長功能區包括：交易展示區、卡車停車場和辦公服務區。輔助功能區包括：后勤保障區、生活服務區、綠化區，以及物流中心儲備用地和道路規劃用地等功能區。

一般將物流區域假設成平面圖，物流中心規劃區域和功能區域形狀為矩形。功能區域的集合為N，且n=[N]為功能區域的數量。假設功能區域的邊分別與物流中心規劃區域坐標圖的X 軸和Y 軸平行，且每個功能區域在進行布局時有橫倒和豎立2 種放置方式，對于功能區i，si=1 表示橫倒，si=0 表示豎立。功能區域放置方式的向量形式為S=(si)n×1，設功能區域i的中心位置坐標di為(xi，yi)，功能區域的中心位置坐標向量表示為d=(di)n×1，則以(d，S)為決策變量的鐵路物流中心功能區布局優化模型如下。

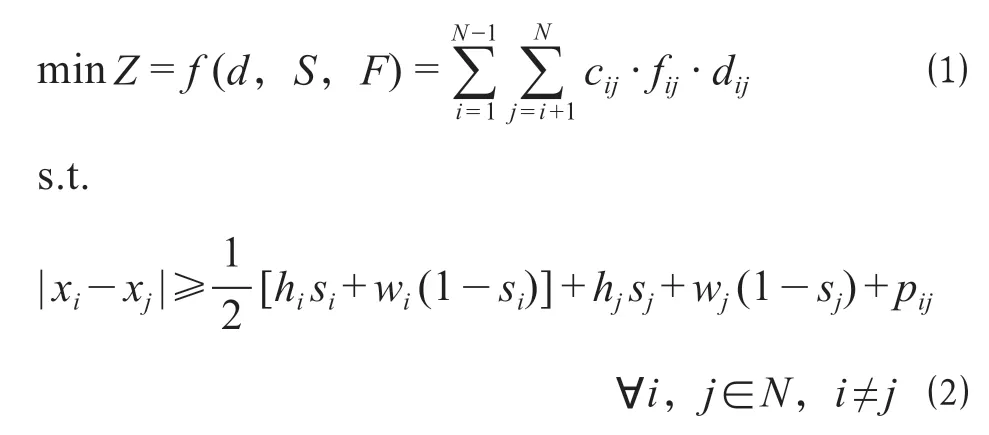
式中：Z為總成本，元；F為fij的向量，F=(fij)n×n，其中，fij為功能區域i與區域j日均物流量，t；cij為單位物流量單位距離的成本，元/ t·m；dij為曼哈頓距離，即dij=|xi-xj|+|yi-yj|，m；hi和hj分別為功能區i和區域j的水平邊長度，m；wi和wj分別為功能區域i和區域j的垂直邊長度，m；pij為功能區邊界之間的最小間距，m；H和W分別為物流中心規劃區域水平邊和垂直邊的長度，m。

對于一般物流區域布局優化包括2 個約束條件。①不重疊約束。兩相鄰功能區域不得相互重疊，如公式⑵—公式⑶。②功能區邊界約束。各功能區的邊界不得超出物流中心規劃區域，如公式⑷—公式⑸。需要注意的是，針對具體的物流區域布局問題，還需增加相應的約束，比如鐵路物流中心功能區布局中存在鐵路裝卸線功能區固定約束、物流中心出入口約束等。鐵路物流中心功能區布局優化模型為非線性混合整數規劃模型，難以用凸規劃算法直接求解，屬于NP 難問題，適宜采用遺傳算法進行求解。

2 改進遺傳算法設計

2.1 分層布局方式改進

遺傳算法的編碼方式對遺傳操作方式及適應度函數均有直接影響，同時也影響算法對于解的搜索能力，包括算法整體計算量和搜索解的質量。對于鐵路物流中心功能區布局優化模型，決策變量為(d，S)，即各功能區域的坐標和放置方式。其中功能區域放置方式可以采用二進制編碼表示。而對于各功能區域坐標，如果直接對其進行編碼，雖然搜索范圍包含了所有解空間，但存在2 個缺點：一是基于一定的精度，對實數區間進行編碼，編碼長度較長，且隨著精度提高，編碼長度也相應增加；二是由于直接對坐標編碼，編碼并沒有考慮約束條件，則大部分解的編碼無效或不正確，且進行遺傳操作時，獲得的解也會包含大量無效解。

設計采用分層思想解決上述問題，分層布局方式主要是針對功能區的整體布局。將規劃區域進行分層，并采用從左到右、從下往上的緊密排列方式對功能區域進行布局，利用自然整數編碼對功能區域布局順序進行編碼，即定義一個功能區域與布局順序一一對應的函數o :N→{1，2，3，…，|N|}。分層思想示意圖如圖1 所示，對7 個功能區域，按照順序從左到右、從下往上分層排列，同時同層緊密排列。由于第1 層容不下功能區域5，所以功能區域5 只能布局在第2 層。采取這種方式布局后記錄各功能區域坐標，獲得該編碼下的布局解。按照這種方式編碼后，每一組編碼均會獲得一個解，且通過這種方式獲得的解的可行度大大增加。

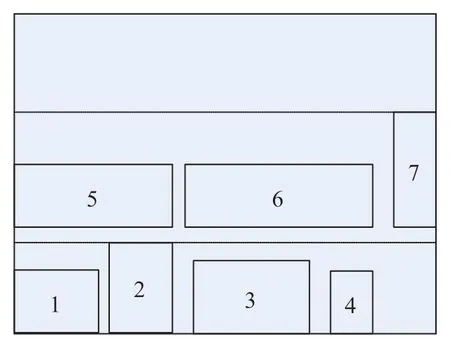
圖1 分層思想示意圖Fig.1 Hierarchical thinking

盡管圖1 所示分層布局方式提高了解的質量，同時也大大削弱了解的搜索能力和搜索范圍。為了同時提高算法搜索解的效率和質量，采用改進的分層思想，按照從左到右、從下往上的緊密堆積方式進行布局，并采用三進制對堆積方式進行編碼。改進分層思想示意圖如圖2 所示。圖2 中，3 個子圖分別表示功能區域7 的3 種堆積方式。

在圖2 的布局方式中，第1 層包括功能區域1～ 4，第2 層包括功能區域5～ 7。對于功能區域7，方式1 是將功能區域7 布局在該區域X 軸范圍內所能放置的最下面；方式2 是將功能區域7 布局在該區域X 軸范圍內最高的水平高度，與該區域X 軸范圍之外的左邊緊挨的第1 個區域水平高度上進行堆積，即在區域4 的水平高度上堆積；方式3 是將功能區域7 布局在第1 層所有功能區域中最高的水平高度基礎上，即在區域2 的水平高度上堆積。

圖2 所示的布局方式，從左到右緊挨著布局，會出現某功能區域無法容納的情況，即超出規劃區域Y 軸邊界。對于這種情況，越界處理方法如圖3 所示。第1 層包含區域1～ 4；第2 層包含區域5～ 7；第3層包含區域8 和區域9；當布局到區域10，且采用堆積方式3，在堆積第4 層時，由于區域10 從最左邊開始布局，剩余豎直高度不夠，造成Y 軸越界，此時找出區域10 的X 軸覆蓋區域中水平高度最高的區域，即區域8，移動區域10 的X 軸，使其布局在區域8 的右邊，重新布局。此時第4 層可以包含區域8。由于采用堆積方式3，則若Y 軸高度不夠，可以降低區域10，使其剛好能布局到規劃區域內為止，此時第4 層包含區域8 和區域10。如果此時仍越界，重復上述過程，直至將區域10 布局到規劃區域內為止，同時記錄各層區域信息。

圖2 改進分層思想示意圖Fig.2 Improved hierarchical thinking

圖3 越界處理方法Fig.3 Cross-border handling method

通過改進分層的布局方法，擴大了原來分層布局方法下搜索解的范圍，同時保持了搜索質量，提高了物流區域布局優化解的搜索效率。

2.2 堆積方式改進

為了進一步擴大解的搜索范圍，對堆積方式進一步改進。改進的堆積方式，主要針對單個功能區域的縱向堆積。當對區域i進行堆積時，找出區域i的X 軸覆蓋的所有區域中的最低水平高度y?i為下限，同時找出前一層中所有區域的最高水平高度yˇi為上限，此時能夠通過參數ri(0 ≤ri≤1)，確定區域i的Y 軸坐標yi如公式 ⑹ 所示。

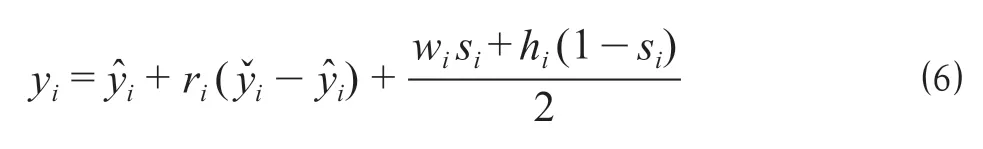
式中：ri表示第i個區域的堆積參數。

同樣以圖2 中區域7 的布局堆積方式為例，區域高度的隨機確定方法如圖4 所示。水平高度上限為d，水平高度下限為0，則確定r7=0.5，則區域7的Y 軸坐標為：r7=0.5d+0.5h7。

圖4 區域高度的隨機確定方法Fig.4 Random determination of area height

對堆積方式的編碼等價于對各區域的堆積參數ri進行編碼，由于任何區域的堆積參數的范圍均為[0，1]的連續區間，則可以利用連續區間的二進制編碼近似表示。

綜上，通過引入堆積參數確定堆積方式，以及相應的編碼方式，進一步擴大了解的搜索空間，同時保持了分層思想的優點，可實現提高搜索解的質量。

2.3 遺傳算子與算法流程設計

采用符號編碼和二進制編碼相結合的方式表示布局問題的解空間。采用二進制編碼{0，1}表示功能區域的放置方式，“0”代表橫放，“1”代表豎放；采用自然數編碼{1，…，N}表示功能區編號，特別將功能區域12 與功能區域10 交換位置，方便更好地求解問題。此外，以[0，1]之間的隨機數對堆積方式進行編碼。每條染色體代表1 種布局方案，用C={Z1，Z2，…，ZN|T1，T2，…，TN|R}表示，其中Zi(1 ≤i≤N)代表功能區域編號；Tj(1 ≤j≤N)代表與之對應的功能區域放置方向；R表示堆積方式。

以目標函數即布局方案的成本函數為適應度函數，對個體的編碼串進行解碼處理，從而得到個體的表現型，由個體的表現型計算出目標函數值。淘汰不滿足要求的染色體，而對于滿足限制條件的個體，以輪盤賭法作為選擇算子。具體操作過程為：對滿足要求的個體進行分類處理，適應度高的個體不需要參與遺傳操作直接進入下一代種群中，以保留優秀的基因，其他個體則采用輪盤賭法從上一代選擇n-1 個個體進行接下來的遺傳操作，使得下一代的種群規模保持不變。對選擇出的個體進行交叉操作，為保證交叉操作的有效性，避免子代無變化情況，采用部分交叉操作方式，即隨機選擇2 個個體，選擇交叉概率下的部分染色體編碼進行交叉映射操作。在進行變異操作時，設計2 種變異方法以增加種群的多樣性，包括基本位變異和交換變異。基本位變異是指對隨機個體的隨機位置產生隨機編碼替代的變異方式；交換變異是指對一條染色體的2 個部分進行交換操作，以獲得新的子代的方式。遺傳算法流程圖如圖5 所示。

圖5 遺傳算法流程圖Fig.5 Flow chart of genetic algorithm

3 算法驗證

采用馮芬玲等[7]研究的算例，設置種群個數為500，最大繁衍代數為100，交叉概率為0.9，變異概率為0.01。分別對簡單堆積方式和改進堆積方式進行求解，從而驗證基于分層思想的改進堆積方式的優化效果。

對分層思想下的簡單堆積方式進行求解，簡單堆積方式的物流區域布局如圖6 所示。由圖6 可知，各功能區域均滿足不重疊約束、功能區域邊界約束、固定約束和物流中心出入口約束。功能區簡單地根據下一層的最高點的縱坐標和各個功能區之間的最短間距約束進行堆積。分層思想下的算法收斂圖如圖7所示。由圖7 可知，遺傳算法收斂速度很快，通過14 代計算，目標函數值快速下降，最后經過100 代遺傳，目標函數值達到6.673 9 萬元。該種方式下，最優染色體為C1={3，11，4，9，6，7，10，8，2，1，5 | 0，0，0，0，0，0，1，1，0，0，0}。由于功能區10 為固定的坐標和放置方向，因此，染色體只考慮了其余11 個功能區，即包含11 個因子。

圖6 簡單堆積方式的物流區域布局圖Fig.6 Layout of logistics area with simple accumulation method

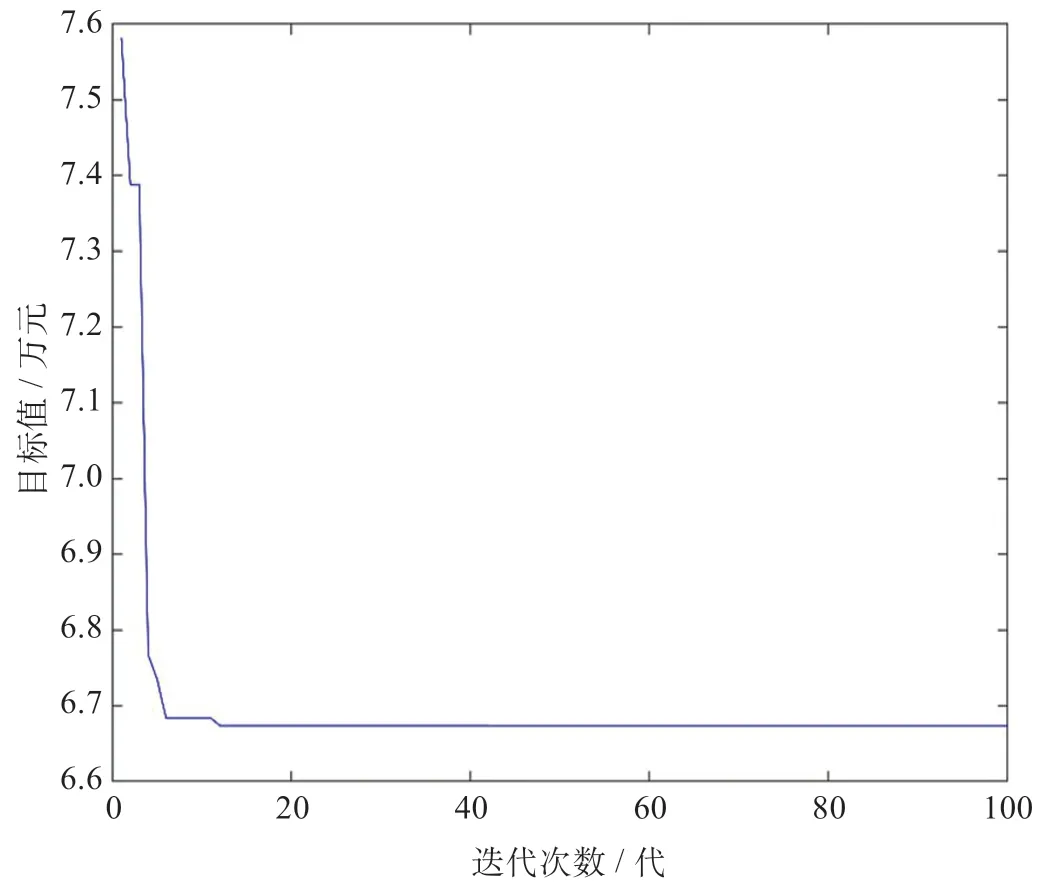
圖7 簡單堆積方式的算法收斂圖Fig.7 Algorithm convergence graph of simple accumulation method

對分層思想下的改進堆積方式算例進行求解，改進堆積方式的物流區域布局圖如圖8 所示。各功能區之間位置更加緊湊，布局更加緊密，得到較為滿意的布局結果。改進堆積方式的算法收斂圖如圖9所示，由圖9 可知，遺傳算法收斂速度很快，通過16 代計算，目標函數值快速下降，最后通過100 代遺傳，目標函數值達到5.887 2 萬元，相比簡單堆積方式的情況，目標值下降了約11.79%。在此方案下，最優染色體為C2={7，3，5，10，4，2，11，6，1，9，8 | 1，1，1，1，0，0，0，0，0，1，0 | 0.750 79}，由此驗證，通過對堆積方式改進，能夠獲得更加優化的目標函數值。

圖8 改進堆積方式的物流區域布局圖Fig.8 Optimized logistics area layout map with improved accumulation method

圖9 改進堆積方式的算法收斂圖Fig.9 Algorithm convergence graph with improved accumulation method

通過計算，2 種方式的最優方案功能區坐標如表1 所示。除了部分特殊功能區的位置較為相似，其他功能區的分布情況截然不同，同時可以看出改進堆積方式的遺傳算法所求解更優。

表1 2種方式的最優方案功能區坐標 mTab.1 Coordinates of the optimal functional area schemes for the two methods

4 結束語

針對求解物流區域布局優化模型，通過改進分層布局方式和堆積方式，設計不同編碼方案，對提高算法搜索解質量，擴大算法搜索解空間具有良好的效果。通過改進前后的遺傳算法對算例求解，表明所改進遺傳算法在短時間內獲得更加滿意的結果，目標值較改進前計算目標值優化11.79%，驗證了改進后的布局方法可以有效降低各功能區之間的物流成本。此外，設計的算法能夠提高整個物流中心的運行效率，從而在競爭日益激烈的物流運輸中，提高鐵路的競爭力。算法基于緊湊型分層思想設計，但是對區域互斥情形考慮不全面，為了繼續擴大搜索解的空間，同時保證解的可行性，可以對每層高度作為決策變量進行進一步優化。