基于模型法對豬舍最佳清理時間的確定

司 展，胡晶晶，宋明亮，周華鋒，郭 軍

（1.沈陽化工大學化學工程學院，遼寧 沈陽 110142；2.東北大學計算機科學與工程學院，遼寧 沈陽 110819；3.沈陽化工大學信息工程學院，遼寧 沈陽 110142；4. 沈陽化工大學理學院，遼寧 沈陽 110142；5. 東北大學軟件工程學院，遼寧 沈陽 110819）

隨著養豬業的集約化和工廠化發展，豬舍的環境控制問題逐漸被人們所重視。在規模化的養殖場中，豬在進食后會產生大量的糞便，而大量糞便堆積往往是影響生豬健康的重要原因。堆積的糞便在豬舍周圍進行水土滲漏則會進一步導致環境污染，同時清理人員的健康也將受到威脅[1-4]。清理豬舍的有效方法一般分為人工清理和機器自動化清理，而目前市場上大多數采用人工清理的方法。基于以上背景，在保證安全的情況下尋找定態化的最佳清理時間，在養殖業的牲畜排泄物清理環節具有廣闊的應用前景，意義重大。

1 定態化模型處理的基本假設

依據經驗可知，生豬廢泄物與生豬數量（n）、飼料喂養量（l）、環境因素（e）等一系列因素有關。

在考察過生豬生長習性、豬舍的環境特征和飼料喂養量后，做出如下假設。

（1）假設所提出的模型基本條件都符合規模化豬養殖的一般規律。

（2）排泄物位置假設。假設生豬糞便排泄物的位置會影響其下次排泄的位置，且呈簡單的負影響。

（3）排泄物分布假設。對于生豬排泄位置變化的宏觀解釋可近似看為豬群環境的熵增過程，其平面隨機自由度為2，其結果也呈現雜亂分布。其排泄物分布面積S（r）與時間（t）大致滿足簡單熱分子隨機分布的模型：

豬舍的環境在特定時間（t）內發生的變化，會引起排泄物分布的變化（圖1）。

圖1 排泄物量隨時間變化量模型

（4）耗糧量假設。假設在提出的所有模型中都科學地使用飼料，依據趙平飛[5]的經驗模型結果來確定生豬在出欄之前所需的耗糧量。當耗糧量一定，運用模型1-2可求出應清理的排泄物總量，所用到的模型如下：

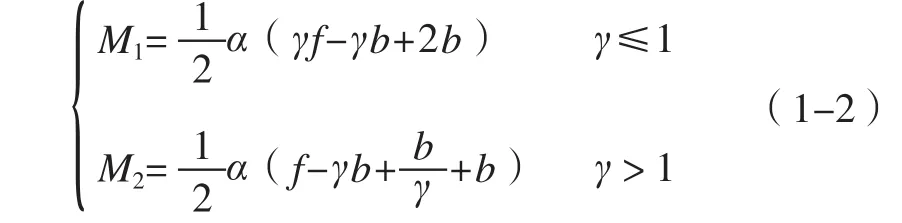
其中M為耗糧量（kg），γ為出欄率（%），b為出欄數（頭），f為存活仔豬數（頭），上述模型是在一定的科學抽象和假設下建立起來的。

（5）假設環境因素對豬排泄物累積量影響符合一般經驗規律。

（6）假設每個豬圈生豬發育狀況大致相同。

（7）假設清理人員的體力耗費過程符合一般肌肉力量下降過程[6-7]。

2 理論模型提出

2.1 環境因素的影響

對豬的生長環境和生活習性進行分析，與之相關的各種因素都會對豬的排泄行為產生影響，當圈舍的布置發生變化（如躺臥區或喂食區的位置互換）時，豬對排泄區選擇亦發生變化。不同的豬個體對環境變化的適應能力存在一定差異，從以往的工作來看，尚無有效的方法得知飼養環境對豬生長后期排泄行為的影響程度。假設豬會去尋找一個較隱私區域（如圈舍的角落處）排泄，同時必須假設上述行為與有限的圈舍空間有關，即圈舍空間中的氣味分布是影響豬選擇排泄位置的重要因素（一般豬使用嗅覺感官的行為發生在排泄行為之前）。

但是，嗅覺對生豬的排泄位置到底有多大影響，目前還無相關資料證實，可根據養殖戶的經驗確定該影響[8]。除此之外，環境中的干燥程度、地表的干凈程度、豬群的聚集程度也會對排泄行為造成影響。本文在定量研究排泄物的累積量的基礎上合理求解最佳清理周期，因此假設φ（e，ζ）用為環境函數代表環境對生豬的排泄物累積量的影響系數，其中ζ為環境修正系數。

2.2 模型的排泄物總量

豬舍的環境在特定時間（t，單位：h）內發生的變化，會引起排泄物分布的變化。由于飼料的喂養量（l）會對排泄物的累積產生影響，加之環境因素的影響[φ（e，ζ）]，可對生豬的排泄物總量[（Ω），單位：kg]進行預測，并對其做出合理假設，結果如下：

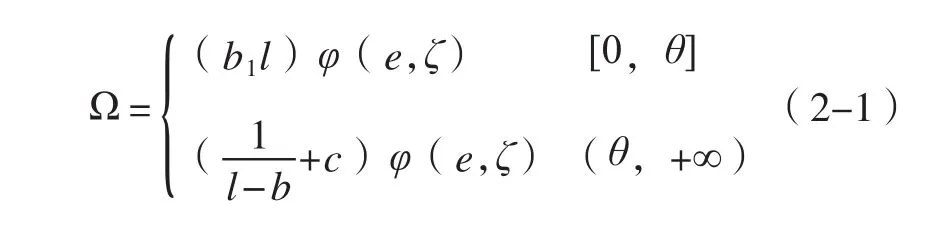
其中，θ取值為飼料投料的飽和點，為經驗點，由養殖戶常規養殖得到。

根據實際情況，可假設該函數連續，為使該模型假設更加嚴格，繼續假設其滿足可導條件，即θ=l當時，滿足如下關系式：

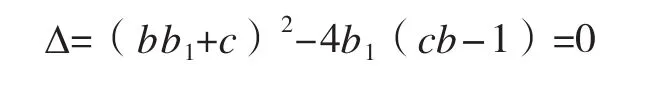
2.3 人工清理中工作效率函數

對于清理人員清理效率的動態表達，可依據李俊紅等在進行個體MET模型的靜態負荷任務推導中所提出的肌肉力量下降過程來描述，可由以下關系表示[6-7]：

考慮到在規模化養殖中排泄物清理的實際需求，僅需考慮工作效率的動態衰變即可，故將上式進行簡化和歸一化處理，得到下式：

2.4 水沖法中清理過程力學分析

沈雪民等通過對豬場排泄物固液分離，及對分離后的固形物發酵、干燥、制粒等測定其物理性質，所測得其濃度與黏度的關系如表1[9]。

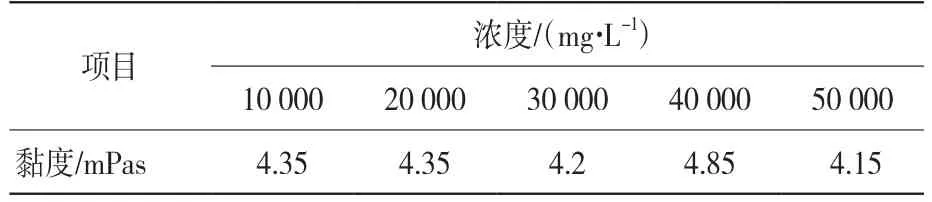
表1 豬排泄物濃度與黏度關系

所得黏度與濃度關系變化不大，故可用平均值代替其物性。計算其平均黏度：4.38 mPas。

又因為黏度與剪應力其中du/dr為流體的運動梯度為常數值1，S為排泄物的表面積，代入（1-1）式，存在如下關系：

該模型中所受剪應力近似等價于沖洗附著力。

2.5 水沖法最佳時間

引入K為生豬的消化常數，結合公式2-1得出清理總量（Ω）與各個相關因素的表達式如下：

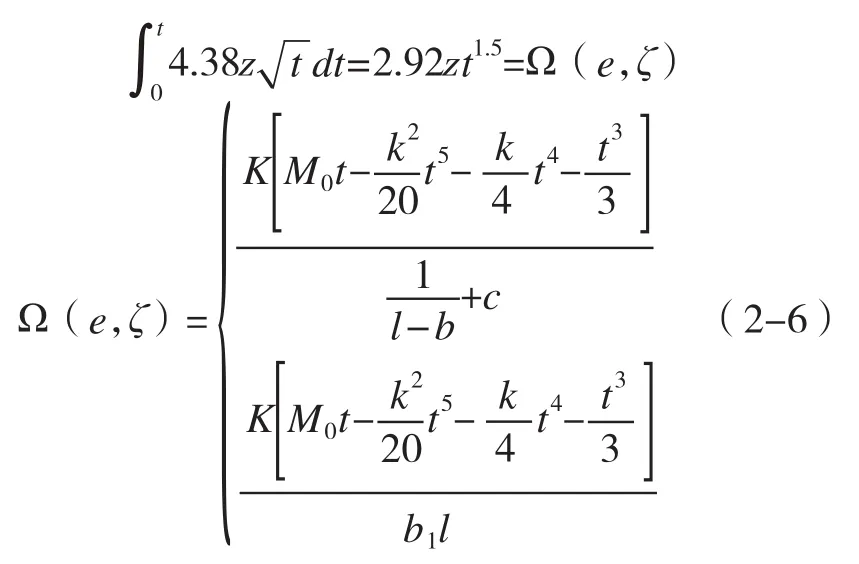
那么就可以通過已知的條件建立起相關的數學模型，求得最佳清理排泄物時間[Ψ（t）]的相應公式：

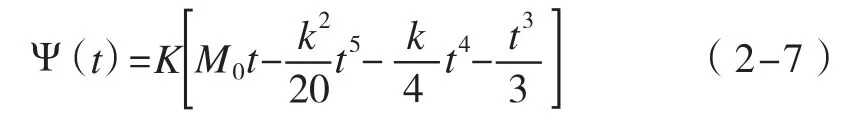
最佳清理周期可通過求解清理量偏導的零點而確定，推導得出最佳清理周期時間如下：

2.6 人工清理最佳時間

定義整個清理周期時間為1，稱為清理周期的當量時間，而對于人工法與機器水沖法的效率與時間模擬結果如圖2。

圖2 水沖法與人工清理法效率變化

由以下解析計算：

也可由數值積分的方式等價同面積下當量時間的數值求解。

3 模型的誤差因素

根據養殖戶的養殖方法得知，養殖戶是不會將生豬隨意分圈的，而是將發育時間大致相同的生豬放在一起，這樣不僅有利于飼料的投放，也便于觀察每個生豬的發展狀況，第2節建立的數學模型也是在每個豬圈生豬發育狀況大致相同的基礎上建立的，同時以忽略分娩時期的母豬情況為前提（表2），以下是以分娩母豬群體為研究對象，得出的在不同生活條件下不同生豬排泄時間和排泄物累積量的狀況。

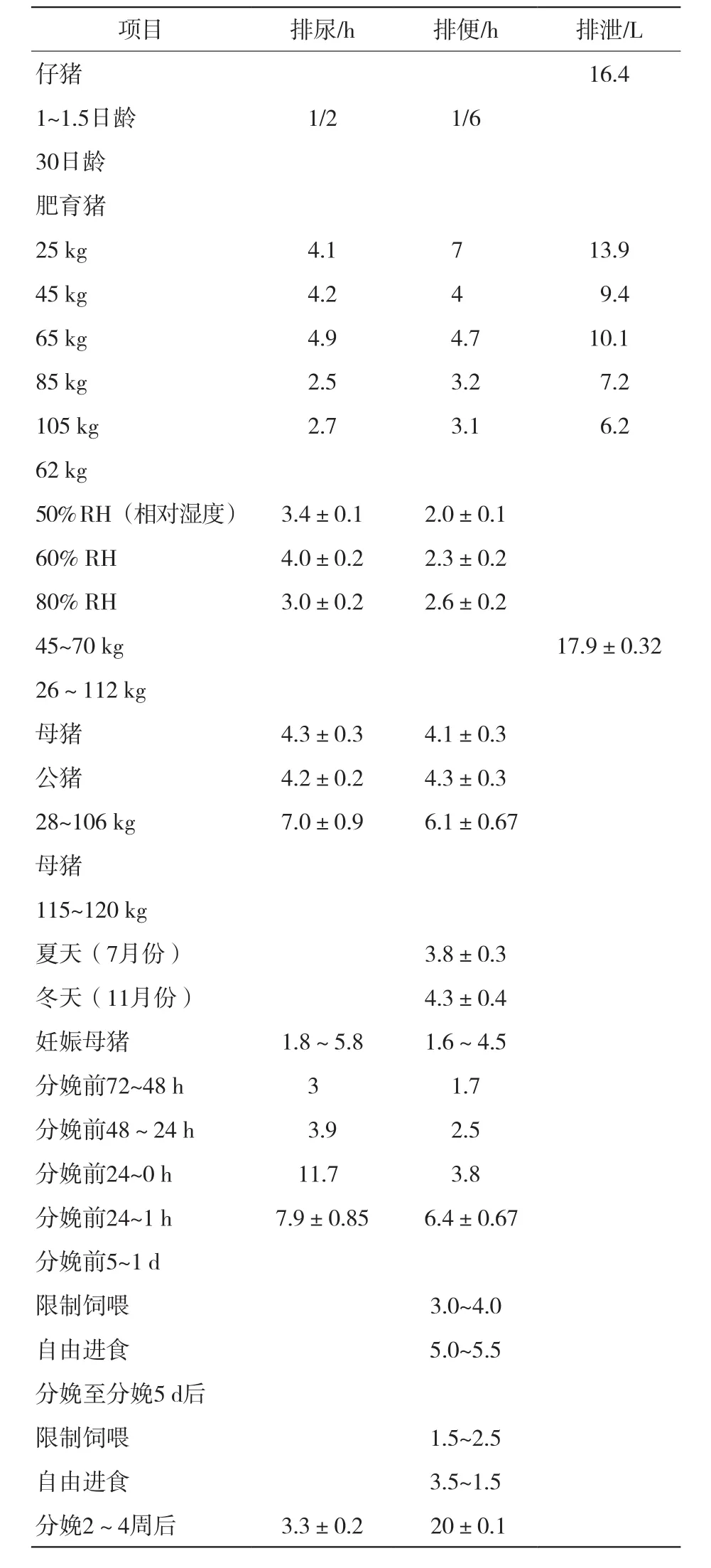
表2 不同特性的生豬排泄時間和排泄物量

表2結果顯示，母豬在分娩前幾天排便頻次相對穩定，在分娩當天則下降（分娩時觀察到限位欄和非限位欄飼養母豬采食量均有所減少）。而第1頭仔豬出生前24 h內母豬排尿和排便次數將有所增加，同時母豬進食時間減少且飲水時間增加。在這期間（第1頭仔豬出生前24 h內）母豬排便和排尿次數增加，說明分娩對于母豬的排泄物累積量有著很大影響[10]。

如果將每個分娩母豬單獨一個豬圈，仔豬的數量影響著圈內的排泄物總量（Ω'）。排除其他因素，假設該豬圈排泄物的總量與豬仔的數量（q）和分娩母豬排泄物總量（c'）有關，假定豬仔數量與圈內的排泄物總量為一次函數相關，k1為一次函數系數（每只豬仔的排泄物量），則總量（Ω'）的相關表達式為：

一般情況下，c'是一個常量，但是隨著母豬分娩時間的改變，c'的數值也會發生相應變化，具體數值可表2所示表格，代入（2-4）方程，得出c'的值，結果顯示，在母豬分娩的不同時間段，圈內的排泄物總量變化較大。

4 模型的精準度改進

假設存在最大排泄物量Ωm，而其影響因素為進食量和消化指數，因此對任意時刻的排泄物量Ω（t）可得到如下關系[11]：

求解可得到：

對此模型有如下的理解：

因此，確定Ωm的值是非常有必要的，這將提升整體模型的精確度和合理性。對于最大排泄物量的確定，依靠于環境容量以及堆糞是對其造成影響的最大安全因素。

5 改進后模型結果

在已確定任意時刻的最大排泄物總量Ωm的基礎上，可確定最佳清理時間。即：

對其偏導以確定最佳清理時間：

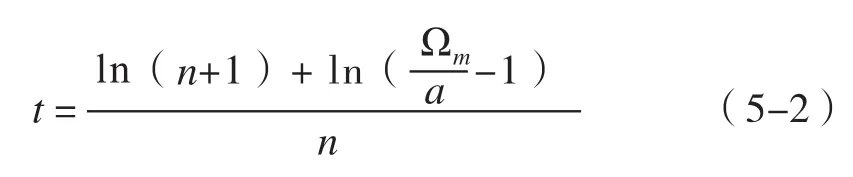
6 模擬模型誤差分析

為了得出更加準確的耗糧量對排泄物總量影響的模型，引入偏好矩陣的概念。利用隨機數生成收斂的偏好矩陣，由此可得出在加入“偏好”時的耗糧量對排泄物總量的影響隨時間變化的模型與真實數據的對比結果（圖3）。

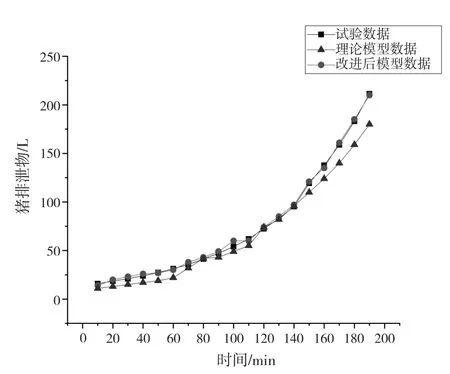
圖3 試驗結果擬合

由圖3可見，模型改進前后和真實的偏差有所不同。其中，理論模型采用多級分段函數，故存有較多不可導點，可采取光滑擬合。其優點就是可利用線性作近似計算。而改進后的模型為平滑曲線，與真實數據擬合較好。

7 模型評價及總結

所提出的排泄物總量的預測模型依賴于對定態化養殖系統的狀態近似及狀態簡化處理，模型的實際解也會隨著客觀因素的變化而變化，模型的不足之處在于較難實現影響因素在此模型中的量化。

定態模型旨在給出簡單的基于經驗和理論指導的數據，引入環境因素及生豬自身因素。而這些因素的定量化往往需要根據實際情況考察確定，因此僅僅通過提出的模型得出的結論會與實際情況有所偏差。

可依據胡凱等的識別算法和深度學習方法對生豬的生活環境和習性進行實時的近期狀態預測，同時引入宋敏等所研究的工作效率的適度性理論，結合本文所提出的模型，給出合理的瞬時最佳清理時間的動態模型[12]，使得所求結果更加準確合理。