基于響應面法的碳管納米流體穩定性

閆素英，張田歌，袁 雪，高 虹，張慧穎，趙曉燕

基于響應面法的碳管納米流體穩定性

閆素英1,2，張田歌1，袁 雪1，高 虹1，張慧穎1，趙曉燕1

（1.內蒙古工業大學能源與動力工程學院，呼和浩特 010051；2. 內蒙古自治區太陽能高效轉化及綜合利用重點實驗室，呼和浩特 010051）

為了獲得穩定性更好的納米流體，基于響應面法對添加優選后分散劑的碳管納米流體進行了穩定性的優化。通過“兩步法”制備碳管納米流體，比較了4種不同類型的表面活性劑對碳管納米流體穩定性和導熱性的影響。以碳管納米流體的粒徑為評價指標，選取碳管納米流體質量分數、超聲振蕩時間、放置時間3個影響因素，設計了三因素三水平Box-Behnken試驗，利用響應面法考察了各因素對納米流體穩定性交互作用的影響。結果表明，含有十二烷基甜菜堿Dodecyl Betaine分散劑的碳管納米流體，在碳管與分散劑比例為1∶2時綜合性能最好。試驗數據建立的二次多項數學模型顯著性極高（<0.000 1），相關系數2=0.964 4，預測值與實際值具有很好的擬合度。通過二次元回歸模型得到影響碳管納米流體穩定性因素的條件為：碳管納米流體質量分數0.27%，超聲時間83.45 min，放置時間8 h。在此條件下的粒徑平均值為121.58 nm，與預測值120.60 nm有0.016%的誤差，說明此模型優化碳管納米流體穩定性是可行的。

納米流體；穩定性；導熱性；分散劑；響應面法

0 引 言

納米流體作為新型的高導熱傳熱介質[1-3]，已經被廣泛的應用于各個領域中。其性能受到眾多因素的影響。納米流體穩定性可通過加入分散劑[4]、調節納米顆粒濃度[5]、超聲時間處理[6]等來改善。故制備出穩定的納米流體是納米流體能否廣泛應用的關鍵因素。

目前，大量學者對納米流體的穩定性進行了研究。Iwaa等[7]研究比較了3種不同類型分散劑對納米流體穩定性和熱物性的影響。Zareei等[8]研究了3種表面活性劑對氧化鋁納米流體的改善程度，但未涉及分散劑與納米流體用量的最佳比例。傳統的正交優化設計方法采用線性數學模型進行試驗設計，具有精度不高、預測性能不佳的缺點，而響應面法采用非線性模型對試驗數據進行高精度的回歸擬合，可以有效地安排和優化試驗。Esfe等[9]通過響應面法對納米流體的熱物性進行了優化，使其粘度和導熱系數達到最優值。Danish等[10]采用響應面法研究了不同因素對二氧化鈦水納米流體粘度和導熱系數的影響，并對建立的模型進行了驗證試驗。Abdulrahman等[11]采用基于多變量設計的響應面法，建立了優化銅納米流體粘度的可行方案，可以較為準確預測銅納米流體粘度的變化。Esfe等[12]利用雜項設計模型進行響應面法研究了不同因素對納米流體熱物性的影響，預測值與試驗數據基本一致。但是使用響應面法對納米流體穩定性優化研究較少，并且對納米流體粒徑的優化還未涉及。

本文通過“兩步法”制備碳管納米流體，對4種不同表面活性劑進行了優選，以粒徑大小為評價指標，考察了各因素對碳管納米流體穩定性的影響規律，確定了影響碳管納米流體穩定性的最佳條件。旨在探討提高納米流體的穩定性，為后續納米流體的制備提供理論依據及試驗基礎。

1 試驗材料和方法

1.1 試驗材料及儀器設備

材料：碳納米管（Carbon Nanotubes，CNTs）納米顆粒，黑色粉狀，純度≥99.9%，外徑>50 nm，平均粒度30 nm，比表面積>60 m2/g，生產廠家為上海超威納米科技有限公司。表面活性劑的詳細參數和試驗設備如表1。

表1 表面活性劑參數

儀器設備：高速剪切機（上海貝爾特B25）；超聲分散儀（豫明儀器YM-1200Y）；馬爾文激光粒度儀（馬爾文公司）；紫外可見近紅外分光光度計（精度±3%，日本島津UV3600）；熱常數分析儀（精度±3%，TPS2500S，Hot Disk AB公司）。

1.2 納米流體的制備過程

本文采用兩步法[13]合成碳管納米流體，將碳管納米粉末分散到蒸餾水中，然后通過高速剪切機將碳管納米流體剪切10 min進一步分散。最后添加分散劑并利用超聲分散儀對碳管納米流體懸浮液進行了不同超聲時間（10、60、110 min）的超聲振動控制[14]，超聲功率可調區間為10～1 200 W，考慮到功率太小超聲時間較長，功率太大溶液溫度過高，所以綜合考慮超聲功率采取800 W。振蕩結束后取出試管，完成碳管納米流體的制備。

1.3 納米流體穩定性評價方法

目前對于納米流體穩定性的評價方法有很多種，本文綜合采用粒度法、Zeta電位法、吸光度法對不同分散劑進行了優選[15-17]。該方法能提高評定分散劑對納米流體穩定性的準確性。

2 響應面試驗設計及模型驗證

響應面法（Response Surface Method，RSM），探究試驗變量和指標的相關性，通過建立響應面圖形并對其進行回歸擬合[18]，可以分析每個影響因素及其相互作用的顯著性，Box-Behnken模型作為RSM中的一個模型，適合多因素間交互作用的研究[19]。

2.1 試驗設計和結果

根據分散劑優選的試驗結果，選取DB-CNTs納米流體的質量分數1、超聲振蕩時間2、放置時間3為自變量，以碳管納米流體粒徑(nm)為響應值。根據Box-Behnken模型，設計三因素三水平響應面分析，水平范圍質量分數選取0.1%～0.5%，超聲振蕩時間選取10～110 min，放置時間選取0～10 d，因素與水平編碼見表2。

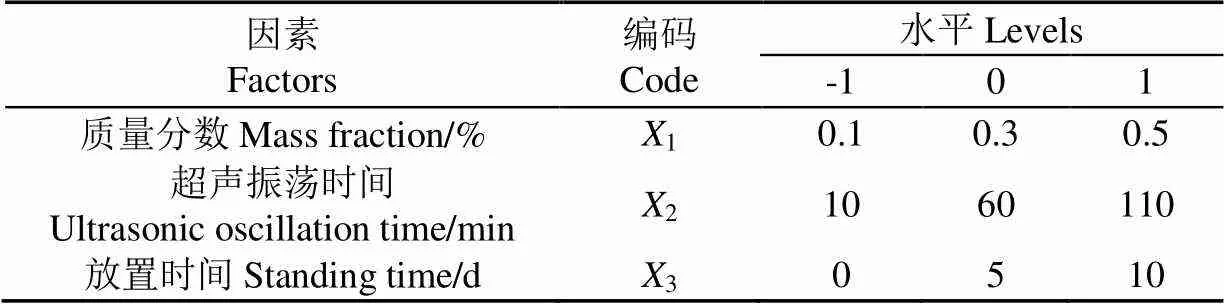
表2 因素水平編碼值表

根據表2各因素水平的編碼值，設計了17組試驗，其中14組為分析試驗，5組為中心試驗，用于試驗誤差的估計。采用Design-Expert軟件分析，建立響應面模型，試驗設計及結果見表3。

通過響應面試驗數據進行二次多元回歸擬合，得到粒徑（）與碳管納米流體質量分數（1）、超聲振蕩時間（2）、放置時間（3）二次回歸方程式為粒徑（）與碳管納米流體質量分數（1）、超聲振蕩時間（2）、放置時間（3）二次回歸方程式為

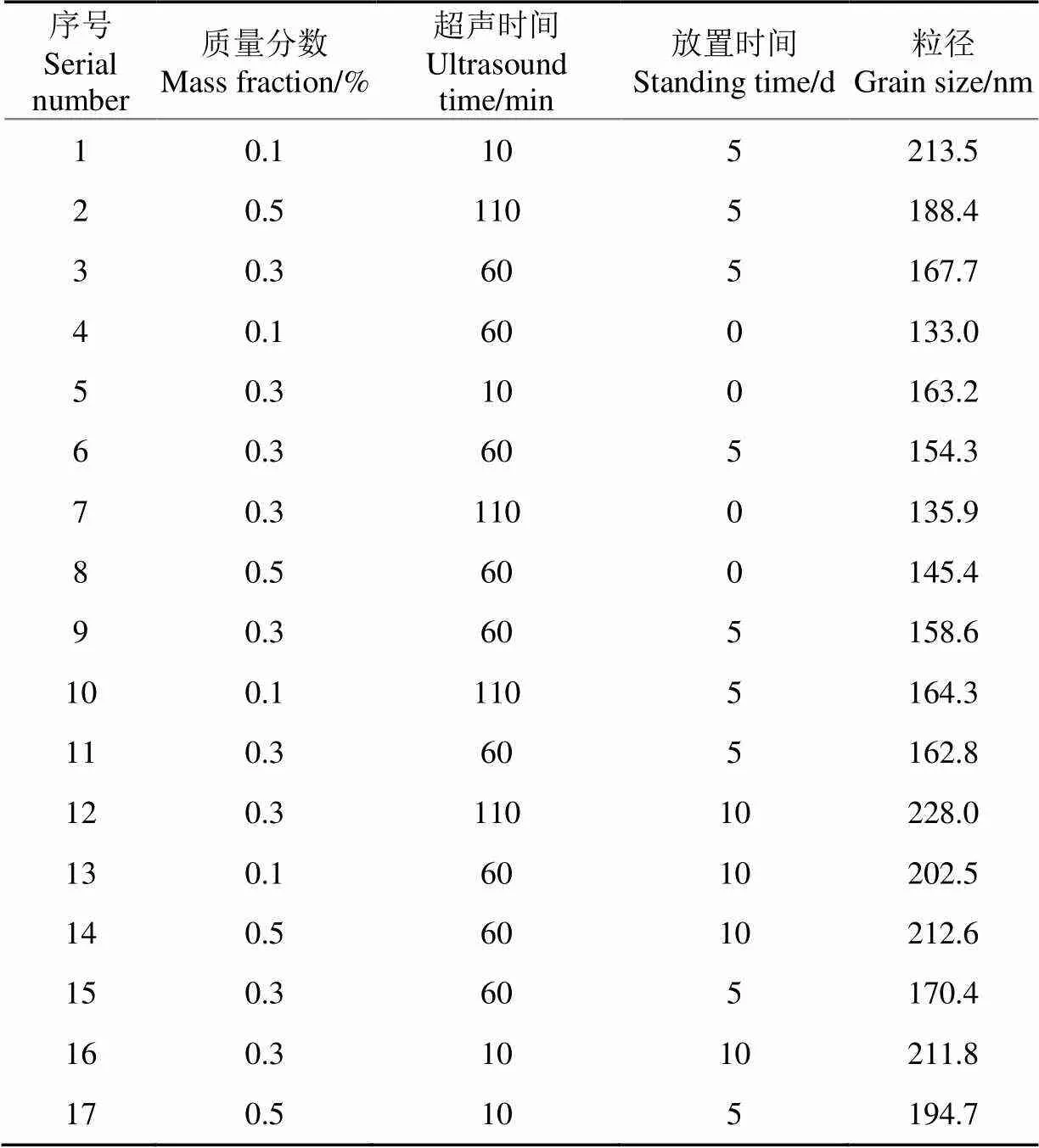
表3 響應面試驗設計及結果

2.2 模型的充分性檢驗

圖1所示的正態概率圖進一步測試了所建立的模型，由圖可知，所有檢查參數的殘差在正態概率圖上大致呈直線，且沒有遵循任何序列或趨勢，這表明殘差是正態且獨立分布的，試驗值合理且均勻[20]。

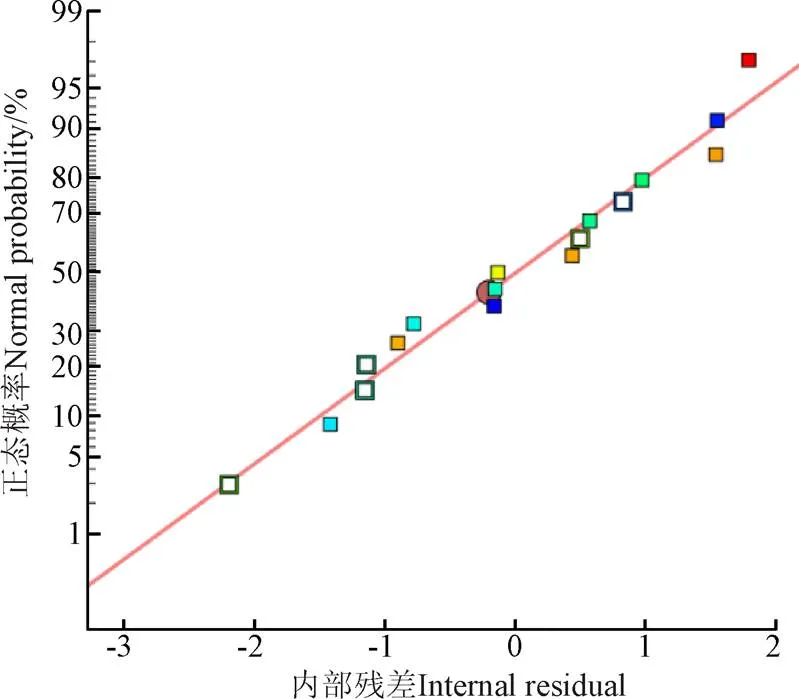
圖1 內部殘差的正態概率圖

圖2為離群點圖被用來檢查任何異常的數據點，如果數據點超過了紅線允許的范圍，本文取±3，那么這些數據點被認為是異常[10]。由圖可知，該模型所有的點都在允許的范圍內且分布散亂無規則，則表明模型是可靠的[21]。

圖3將粒徑的試驗結果與模型預測的數據進行了比較，由圖可知，實際值與預測值呈現正相關性，在斜率為1的直線兩側分布較為均勻，模型和試驗數據之間有很好的一致性。因此使用統計方法得到的試驗結果與預測結果之間有很好的相關性。

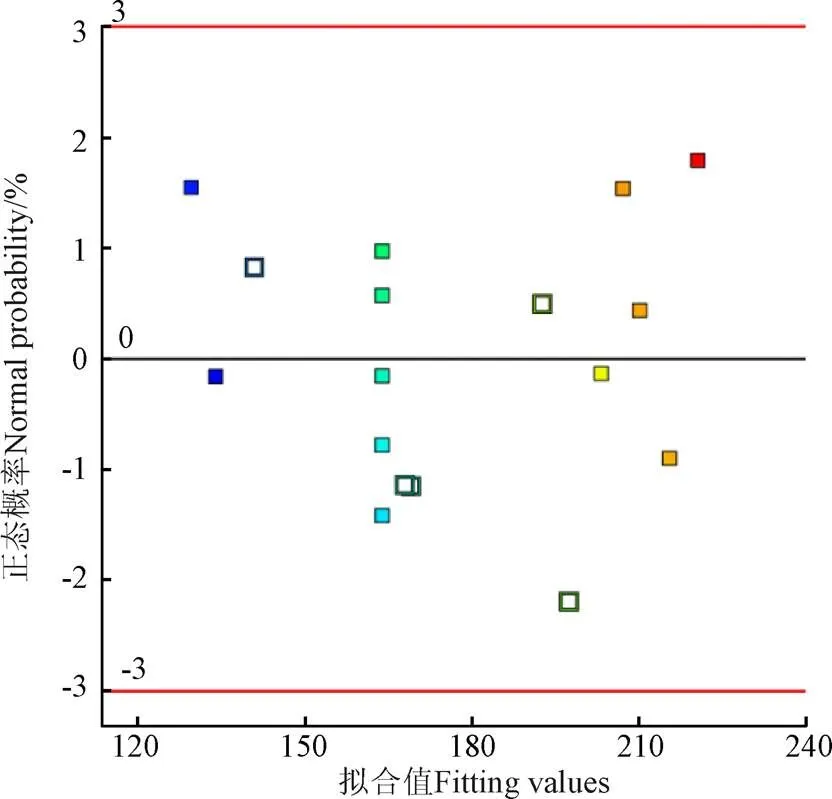
圖2 離群點圖

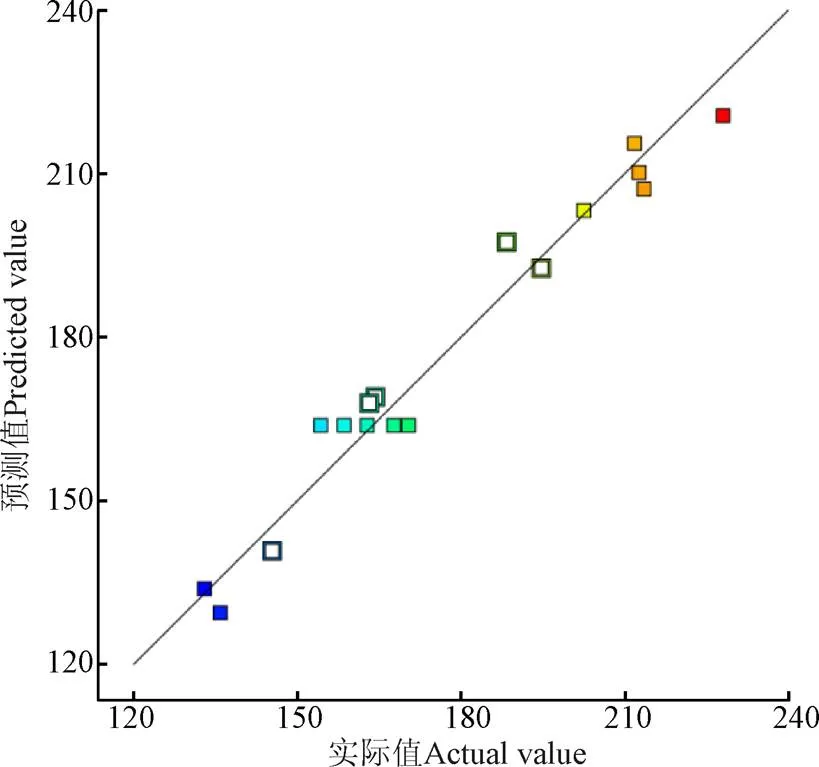
圖3 預測值與實際值對比圖

2.3 模型方差分析

為進一步確定1、2、3這3個因素對納米流體粒徑的影響程度，對回歸模型給出的方差進行分析，結果見表4。概率值越小，相應變量的顯著程度越高[22]。在本試驗中，計算值為34.9，值小于0.000 1，說明所得模型具有很高的顯著性。其校正系數2=0.964 4，模型擬合度好。此外失擬項值為1.46，值為0.366 5大于0.05，說明模型的有效性無統計學意義。因此，該回歸方程的模型成立。

由上表4可知，在一次項中，放置時間3的影響最大（<0.000 1），達到極顯著水平，超聲時間2達到顯著水平（=0.010 8<0.05）。在二次項中CNTs納米流體質量分數12達到顯著水平（=0.047 7<0.05），超聲振蕩時間22達到極顯著水平（=0.000 4<0.01）。在交互項中，CNTs納米流體質量分數和超聲時間的交互項12達到顯著水平（=0.017 1<0.05），超聲時間和放置時間的交互項23達到顯著水平（=0.016 0<0.05）。而13、32對碳管納米流體粒徑的影響均不顯著（>0.05）。由碳管納米流體粒徑可知，3個影響因素（見表2）對納米流體粒徑的主次因素為：3>2>1。

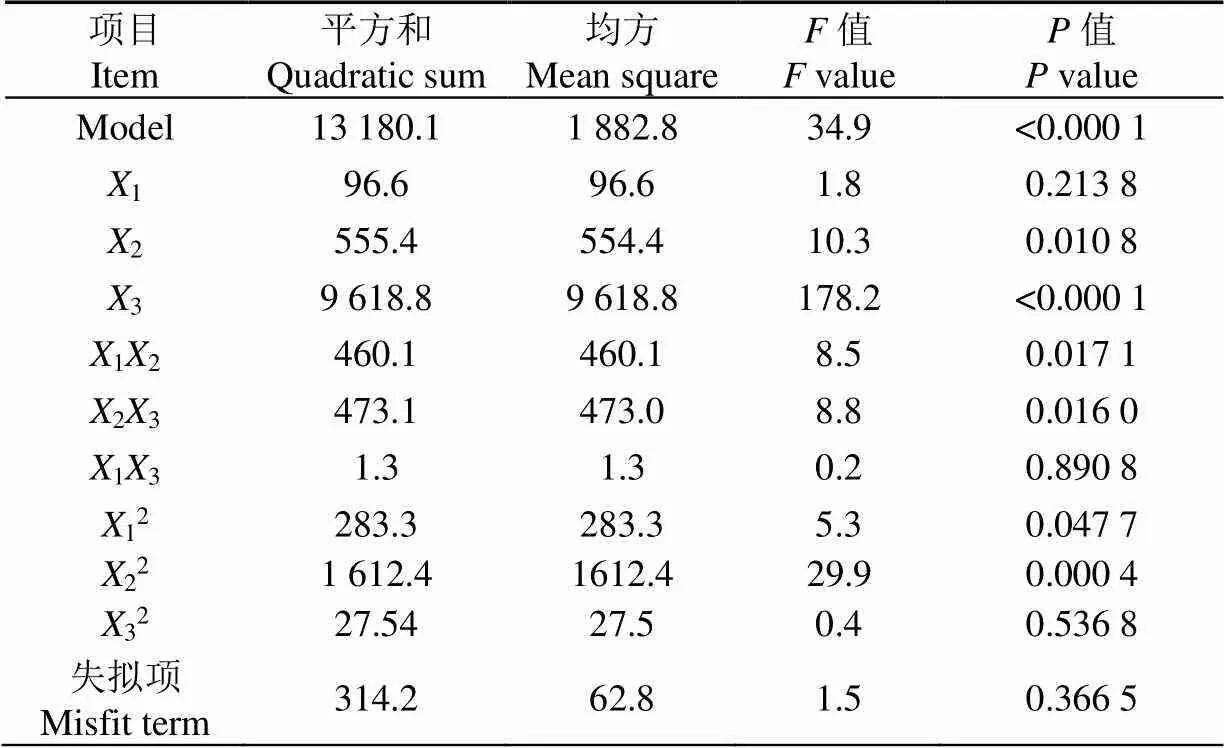
表4 回歸模型方差分析結果

注：<0.05，差異顯著；<0.01，差異極顯著。

Note:<0.05, the difference was significant;<0.01, the difference was significant.

3 結果與討論

3.1 分散劑對納米流體穩定性的影響及優選

3.1.1 粒徑

圖4顯示了CNTs與分散劑在5種配比和5種放置時間下納米流體平均粒徑的試驗結果。由圖可知，DB-CNTs、CTAC-CNTs、Tx-100-CNTs和SDS-CNTs納米流體隨著分散比例的增加呈現先減小后增大的趨勢，并分別在比例為1∶2，1∶2，1∶1，1∶2時粒徑呈現最小值，這是因為此時納米顆粒表面提供分散劑吸附的面積已經飽和，納米流體分散穩定性較好，可以看出添加最佳添加量的分散劑可以提高納米流體的穩定性[23-24]。

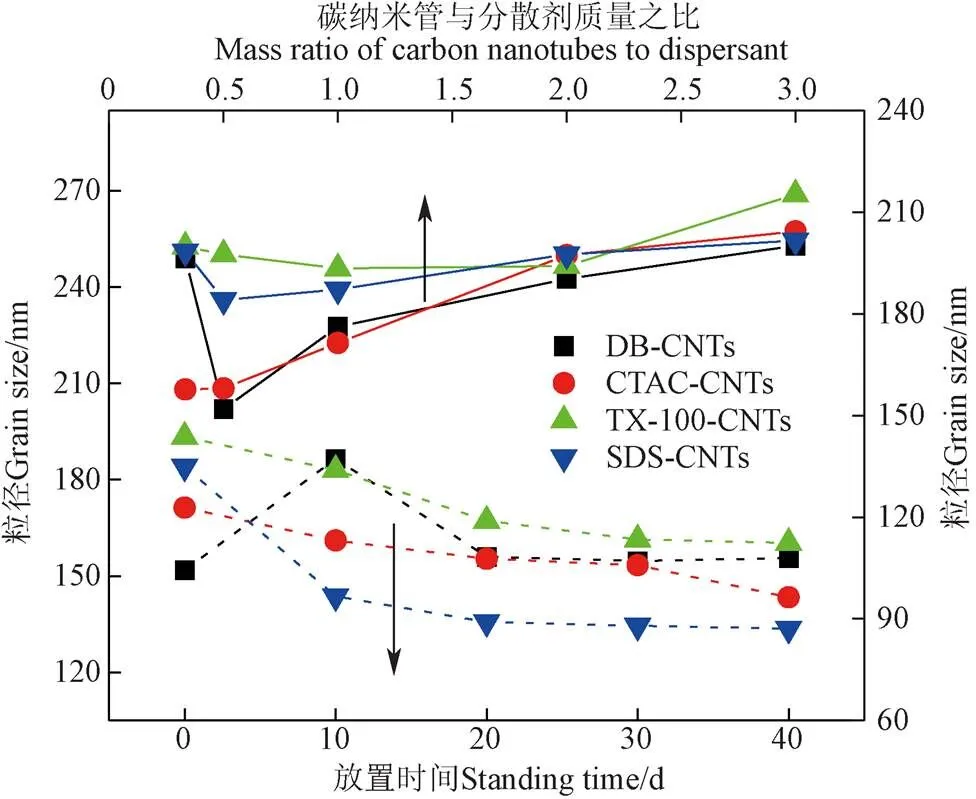
注：DB-CNTs等表示添加DB分散劑的碳管納米流體，其中前綴表示添加的分散劑種類，后綴表示碳管納米流體，下同。其中實線對應右縱坐標，虛線對應左縱坐標。

由圖4可知，DB納米流體放置10 d粒徑發生較大的增大，可能是由于懸浮液中出現團聚現象，粒子體積增大，懸浮液中大體積的顆粒發生沉降現象，之后逐漸變小后趨于平緩，CTAC-CNTs、Tx-100-CNTs和SDS-CNTs納米流體的粒徑逐漸減小并趨于平緩。

3.1.2 Zeta電位

圖5顯示了不同分散劑含量及放置時間對CNTs納米流體Zeta電位的影響。由圖可知，隨著表面活性劑比例的增加，含有SDS和CTAC的納米流體產生更高的值，在比例為1:2時產生最大電位絕對值分別為40.4和28.4 mV，Zeta電位絕對值越大，說明此時納米流體分散體系越穩定。含有DB納米流體的Zeta值較小，整體在?20 mV附近波動。

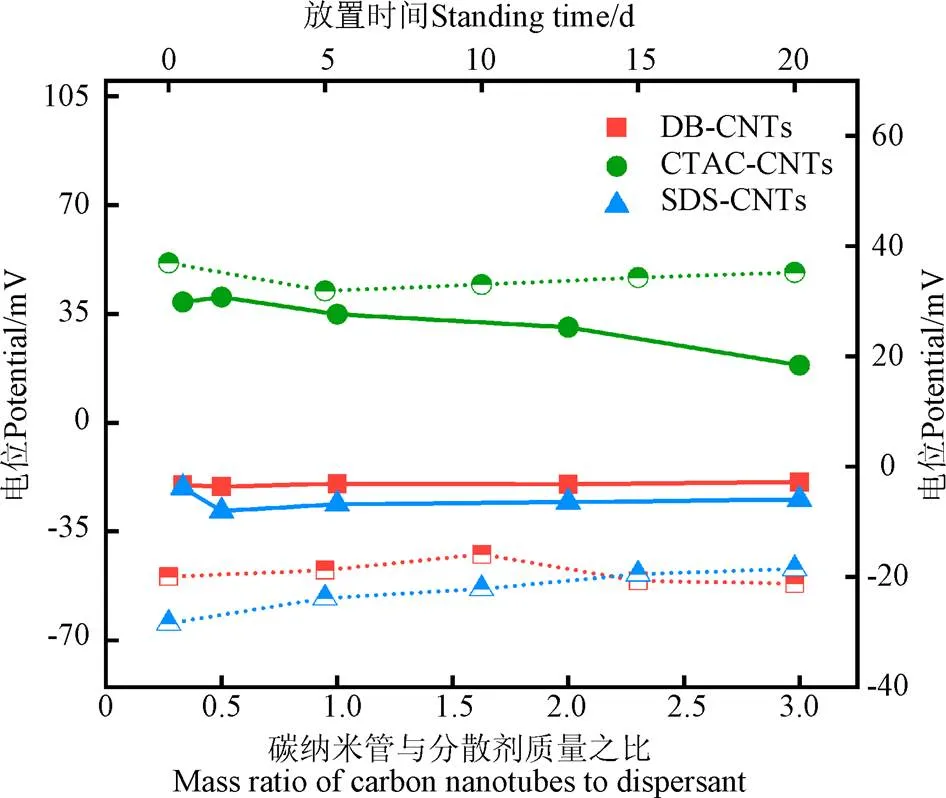
注：實線為分散劑比對應左縱坐標。虛線為放置時間對應右縱坐標。

由圖5可知，DB-CNTs納米流體的Zeta電位絕對值呈先減小后增大的趨勢，在放置10 d取得最小電位絕對值15.6 mV。SDS-CNTs納米流體電位負值一直呈現減小的趨勢，說明穩定性不斷下降。CTAC-CNTs納米流體的Zeta電位變化趨勢不明顯。

3.1.3 吸光度

圖6顯示了分散在的水中添加不同比例分散劑的CNTs的UV-vis光譜。通過分光光度法[25]比較分散的CNTs在波長為301 nm的光譜。

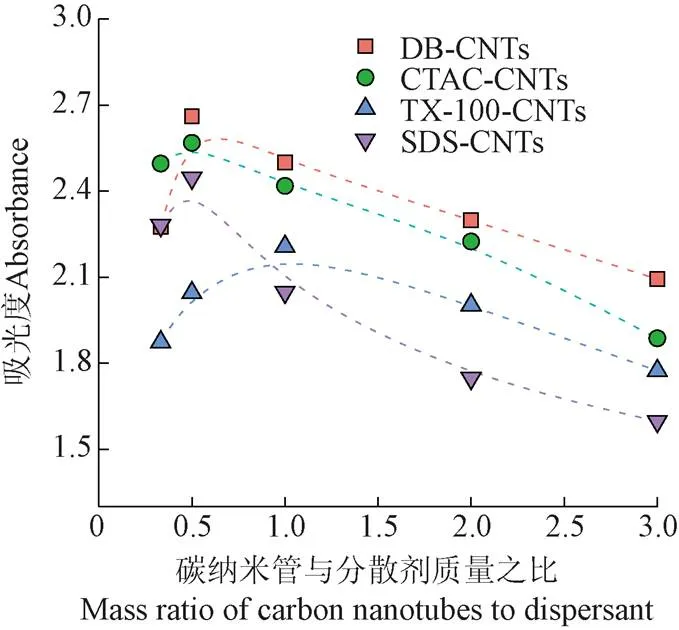
圖6 不同分散劑比例對吸光度的變化曲線（波長301 nm）

可以看到使用DB表面活性劑的納米流體在比例為1∶2時具有最高的吸光度，接著是具有CTAC的納米流體，然后是SDS的納米流體，最后是Tx-100。這是由于兩性表面活性劑DB對碳基納米材料的吸附高于其它離子表面活性劑，兩性表面活性劑分子的一頭帶負電荷和另一頭帶的陽離子電荷之間存在強靜電相互作用[26]，使得納米流體具有良好的分散性。

3.2 分散劑對導熱性能的影響

圖7顯示了添加不同比例分散劑下碳管納米流體的導熱系數。由圖可知，4種納米流體隨著分散比例的增加，導熱系數均是先增大后減少的趨勢，含有分散劑DB的碳管納米流體具有最高的熱導率。DB-CNTs，CTAC-CNTs，Tx-100-CNTs和SDS-CNTs 4種納米流體的比例分別為1∶2，1∶1，1∶2，1∶2時導熱系數呈現最大值，導熱系數分別為0.687 9、0.682 3、0.675 1和0.674 7 W/(m·K)。

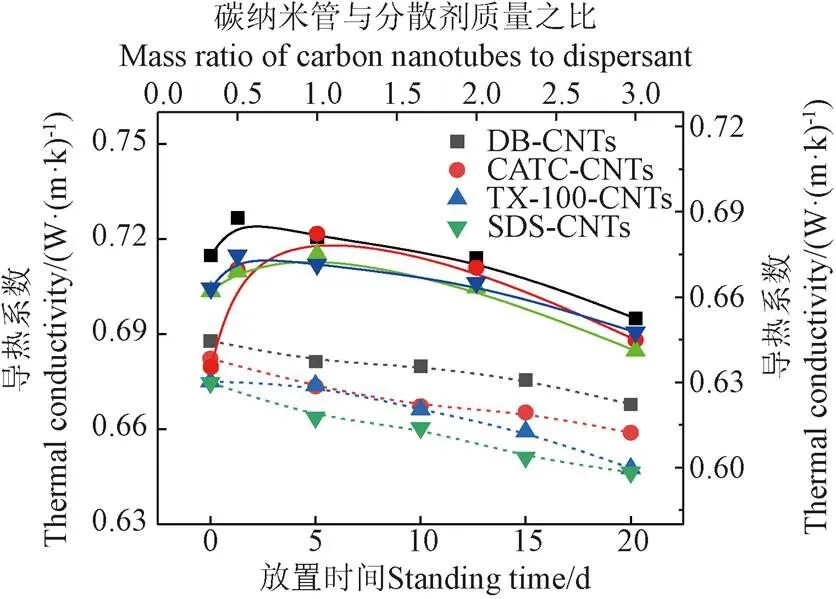
注：實線分散劑比對應右縱坐標。虛線放置時間對應左縱坐標。

由圖7可知，DB-CNTs、CTAC-CNTs、Tx-100-CNTs、SDS-CNTs納米流體導熱系數隨著放置時間得到了明顯的變化，幾乎呈線性下降，下降速率較快的是SDS-CNTs。

通過使用電位、粒徑、吸光度和導熱系數來評價分散劑-CNTs流體的整體性能，結果表明，與其他3種分散劑相比，含有DB分散劑的CNTs納米流體，在碳管與分散劑比例為1∶2時的粒徑最小、吸光度最高、導熱系數最高，被認為是碳管納米流體穩定的最佳比例。因此選用DB分散劑去研究CNTs納米流體的性能。

3.3 碳管納米流體穩定性的響應面分析

通過等高線圖的形狀可以得出各影響因素交互作用的大小，橢圓形代表著交互效應明顯，而圓形則代表兩者交互作用不明顯[27]。而響應曲面變化的越快表示坡度越大，即對試驗結果的影響更為顯著。

3.3.1 質量分數與超聲時間

圖8為碳管納米流體質量分數與超聲時間兩因素交互作用的等高線圖。由圖8可知，粒徑隨著質量分數和超聲時間的增加均呈現先增大后減小的趨勢，說明質量分數過大反而不利于碳管納米流體的穩定性提高[28]，而超聲時間過長，納米粒子在超聲比作用下劇烈運動，導致已經均勻分散的納米顆粒劇烈碰撞凝聚使得體積變大，從而產生沉淀使得穩定性變差[29-30]。等高線圖呈現橢圓形，說明兩者的交互作用明顯。

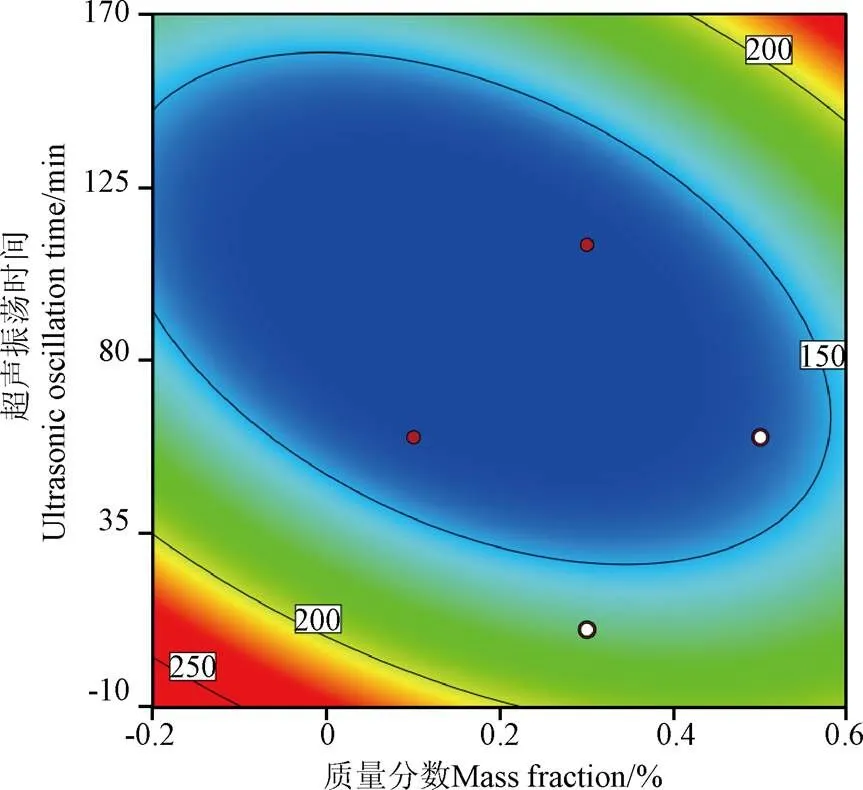
圖8 質量分數與超聲時間的等高線圖

3.3.2 超聲時間與放置時間

圖9為超聲振蕩時間與放置時間兩因素交互作用的等高線圖。由圖9可知，粒徑隨著超聲振蕩時間的增加呈現先減小后增大的趨勢，隨放置時間的增加而增加。粒徑值在超聲振蕩時間為83.45 min左右較小，這是因為超聲振蕩使溶液的溫度升高，加速了納米顆粒的分子熱運動，從而有利于納米顆粒克服重力在溶液中穩定懸浮[31]。等高線不呈橢圓形，說明兩者的交互作用不明顯。

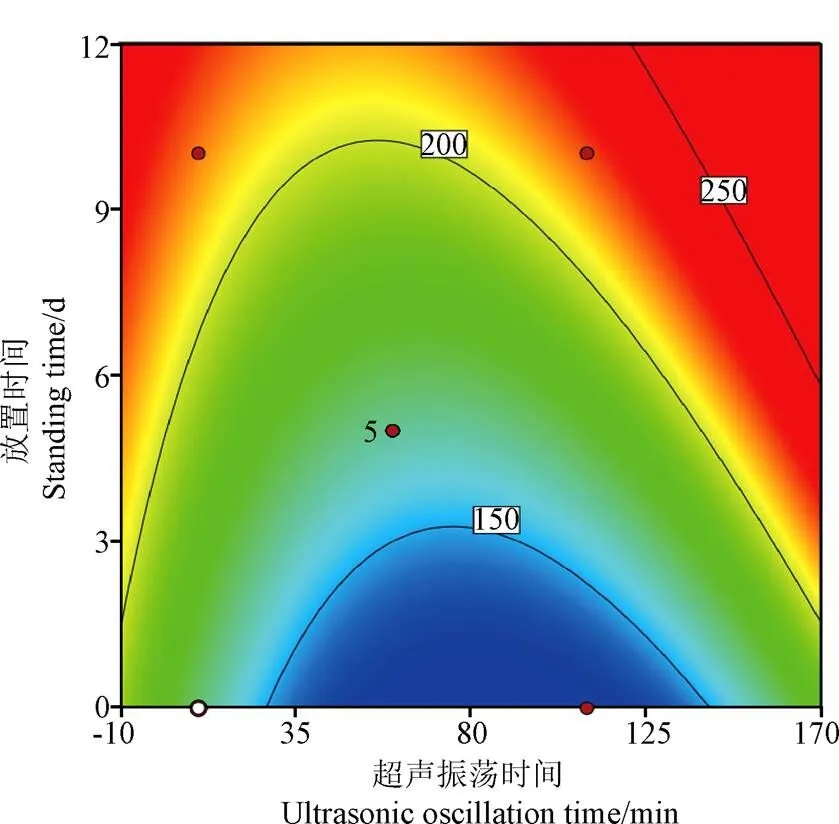
圖9 超聲時間與放置時間的等高線圖

3.3.3 質量分數與放置時間

圖10為質量分數與放置時間兩因素交互作用的等高線圖。由圖10可知，粒徑隨著質量分數的增加呈先減小后增大的趨勢，隨放置時間的增加而增加。當碳管納米流體質量分數過大時，碳納米管間相互纏繞的幾率變大，從而導致納米流體整體粘度的增加，使得溶液穩定性變差。等高線不呈橢圓形狀，說明兩者的交互作用不明顯。以上結論與方差分析一致，驗證了與試驗模型的擬合結果。

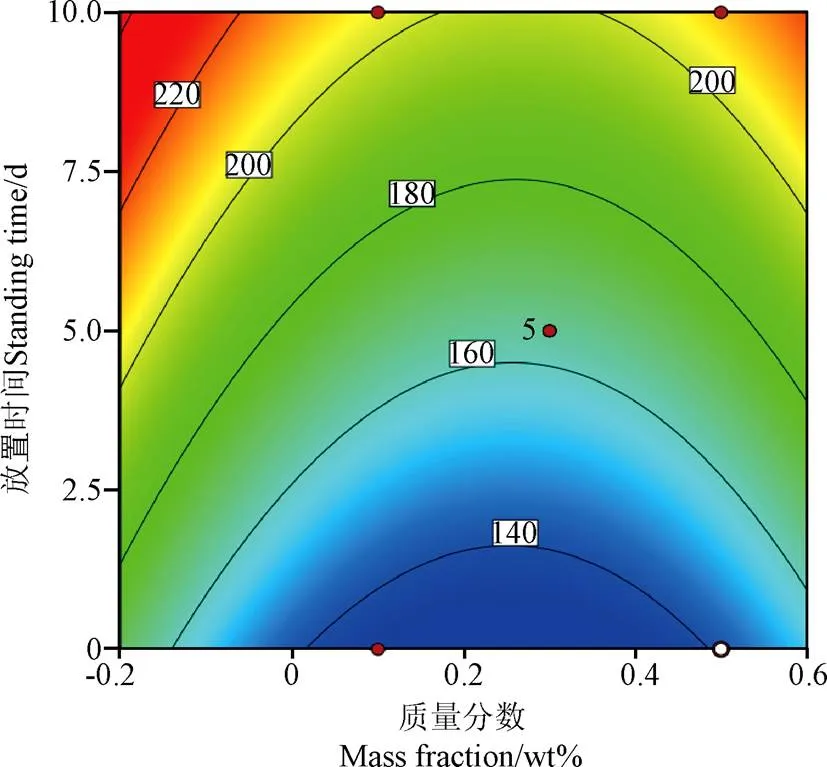
圖10 質量分數與放置時間時間的等高線圖

3.4 優化與驗證

由響應面優化粒徑所得最佳影響粒徑的條件為DB-CNTs質量分數為0.27%，超聲振蕩時間為83.45 min，放置時間為8 h，粒徑值為121.60 nm。采用最佳條件進行了3次驗證試驗，所得到的粒徑分別為121.57、121.55、121.62 nm，所得平均值為121.58 nm，與理論值預測偏差0.016%，實際值與預測值接近，具有一定的參考價值。通過響應面試驗分析可知，在后續的納米流體制備中，盡量選好超聲振蕩時間和放置時間，以提高納米流體的穩定性。

4 結 論

本文針對納米流體穩定性問題，篩選出合適的分散劑，利用響應面模型與試驗數據相結合的方法對納米流體的穩定性進行了分析優化，主要結論如下：

1）通過試驗對比分析了分散劑對碳管納米流體穩定性和導熱性能的影響。結果表明，與其他3種分散劑相比，含有DB分散劑的CNTs納米流體，在碳管與分散劑比例為1:2時的粒徑最小、吸光度最高、導熱系數最高，因此選用DB分散劑去研究CNTs納米流體的性能。

2）基于Box-Behnken試驗設計方法，獲得了能準確描述碳管納米流體粒徑值的響應面模型，同時獲得響應值粒徑（）與碳管納米流體質量分數（1）、超聲振蕩時間（2）、放置時間（3）的二次多項回歸方程。

3）通過顯著性分析可知，對于碳管納米流體粒徑而言，3個因素對其影響的顯著程度為：放置時間>超聲振蕩時間>CNTs納米流體質量分數。其中CNTs納米流體質量分數與超聲振蕩時間交互作用明顯，超聲振蕩時間與放置時間的交互作用不明顯，CNTs納米流體質量分數與放置時間的交互作用不明顯。

4）在試驗的基礎上，設計了三因素三水平響應面，得到最小粒徑下各影響因素的條件：CNTs質量分數0.27%、超聲振蕩時間83.45 min、放置時間8 h，預測粒徑值121.60 nm與實際平均值121.58 nm偏差0.016%。本文的研究為后續提高納米流體穩定性提供理論依據和試驗基礎。

[1] Mehdi B, Saeed H. Electronics cooling with nanofluids: A critical review[J]. Energy Conversion and Management, 2018, 172: 438-456.

[2] 李龍，王江，翟玉玲，等. CuO-ZnO混合納米流體導熱系數影響分析[J]. 工業加熱，2019，48(3)：38-40.

Li Long, Wang Jiang, Zhai Yuling, et al. Analysis ofthermal conductivity of CuO-ZnO nanofluids in ethyleneglycol/water mixture[J]. Industrial Heating, 2019, 48(3): 38-40. (in Chinese with English abstract)

[3] Taghizadeh A, Taghizadeh M, Azimi M, et al. Influence of cerium oxide nanoparticles on thermalconductivity of antifreeze[J]. Journal of Thermal Analysisand Calorimetry, 2020, 139(4): 225-236.

[4] 李棟，吳洋洋，劉昌宇，等. 分散劑對Al2O3-paraffin納米流體吸收太陽能的影響[J]. 工程熱物理學報，2019，40(7)：5.

Li Dong, Wu Yangyang, Liu Changyu, et al. Effect of surfactant on solar energy absorption of Al2O3-paraffin nanofluids[J]. Journal of engineering thermophysics, 2019, 40(7): 5. (in Chinese with English abstract)

[5] Xla C, Wc B, Cz B. The stability, viscosity and thermal conductivity of carbon nanotubes nanofluids with high particle concentration: A surface modification approach[J]. Powder Technology, 2020, 361: 957-967.

[6] Urmi W T, Rahman M M, Kadirgama K, et al. An overview on synthesis stability opportunities and challenges of nanofluids[J]. Materials Today: Proceedings, 2021, 41: 30-37.

[7] Iwaa B, Adma C, Am A, et al. An experimental study on stability and thermal conductivity of water/CNTs nanofluids using different surfactants: A comparison study[J]. Journal of Molecular Liquids, 304, 2020, 111025.

[8] Zareei M, Yoozbashizadeh H, Hosseini H. Investigating the effects of pH, surfactant and ionicstrength on the stability of alumina/water nanofluids using DLVO theory[J]. Journal of Thermal Analysis and Calorimetry, 2018, 135(2): 1185-1196.

[9] Esfe M H, Amiri M K, Bahiraei M. Optimizing thermophysical properties of nanofluids using response surface methodology and particle swarm optimization in a non-dominated sorting genetic algorithm[J]. Journal of the Taiwan Institute of Chemical Engineers, 2019, 103: 7-19.

[10] Danish M, Yahya S M, Saha B B, et al. Modelling and optimization of thermophysical properties of aqueous titania nanofluid using response surface methodology[J]. Journal of Thermal Analysis & Calorimetry, 2020, 139(5): 3051-3063.

[11] Abdulrahman A. Modeling and optimization of dynamic viscosity of copper nanoparticles dispersed in gear oil using response surface methodology[J]. Materials Today: Proceedings, 2021, 42: 771-775.

[12] Esfe M H, Firouzi M, Rostamian H, et al. Prediction and optimization of thermophysical properties of stabilized Al2O3/antifreeze nanofluids using response surface methodology[J]. Journal of Molecular Liquids, 2018, 261: 14-20.

[13] 孫恩博，陳今茂，熊春華，等. 納米流體穩定性及其導熱性能研究[J]. 熱能動力工程，2021，36(5)：61-65.

Sun Enbo, Chen Jinmao, Xiong Chunhua, et al. Research on the stability and thermal comductivity of nanofluids[J]. Journal of Engineering for Thermal Energy and Power, 2021, 36(5): 61-65. (in Chinese with English abstract)

[14] Zhang H, Yan S, Wang T, et al. Enhanced heat transfer of carbon nanotube nanofluid microchannels applied on cooling gallium arsenide cell[J]. Journal of Thermal Science, 2020, 29(6): 1475-1486.

[15] Mahbubul I M, Elcioglu E B, Amalina M A, et al. Stability, thermophysical properties and performance assessment of alumina?water nanofluid with emphasis on ultrasonication and storage period[J]. Powder Technology, 2019, 345: 668-675.

[16] Aziz S, Khalid S, Khalid H. Influence of surfactant and volume fraction on the dispersion stability of TiO2/deionized water based nanofluids for heat transfer applications[J]. Materials Research Express, 2019, 6(1): 015031.

[17] Han Xiaofei, Lu Liwei, Yan Suying, et al. Stability, thermal conductivity and photothermal conversion performance of water-based ZnO nanofluids[J]. 熱科學學報：英文版, 2021, 30(5):1581-1595.

[18] 王功亮，姜洋，李偉振，等. 基于響應面法的玉米秸稈成型工藝優化[J]. 農業工程學報，2016，32(13)：223-227.

Wang Gongliang, Jiang Yang, Li Weizhen, et al. Process optimization of corn stover compression molding experiments based on response surface method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(13): 223-227. (in Chinese with English abstract)

[19] 張續成，亓偉，徐艷，等. 響應面法對磁性碳基固體酸催化劑的制備工藝優化研究[J]. 太陽能學報，2018，39(9)：7.

Zhang Xucheng, Qi Wei, Xu Yan, et al. Optimization of preparation process of magnetic carbon based solid acid catalyst by Response Surface Methodology[J]. Journal of Solar Energy, 2018, 39(9): 7. (in Chinese with English abstract)

[20] Esfe M H. Investigation the effects of different nanoparticles on density and specific heat： Prediction using MLP artificial neural network and response surface methodology[J]. Colloids and Surfaces A-physicochemical and Engineering Aspects, 2022, 645.

[21] Esfe M H, Alidoust S, Asdershiri E M, et al. Comparative rheological study on hybrid nanofluids with the same structure of MWCNT (50%)-ZnO(50%)/SAE XWX to select the best performance of nano-lubricants using response surface modeling[J]. Colloids and Surfaces A-physicochemical and Engineering Aspects, 2022, 641.

[22] 李學琴，時君友，亓偉，等. 響應面法優化生物質基固體酸催化劑的制備[J]. 太陽能學報，2015，36(5)：5.

Li Xueqin, Shi Qunyou, Qi Wei, et al. Optimization of preparation of biomass based solid acid catalyst by response surface methodology[J]. Journal of Solar Energy, 2015, 36(5): 5. (in Chinese with English abstract)

[23] 夏國棟，李奧，馬丹丹. 鉑錫合金納米流體導熱系數與穩定性影響因素分析[J]. 北京工業大學學報，2021，47(9)：8.

Xia Guodong, Li Ao, Ma Dandan. Analysis of factors influencing the thermal conductivity and stability of PtSn nanofluids[J]. Joural of Beijing University of Technology, 2021, 47(9): 8. (in Chinese with English abstract)

[24] 丁潔，王平，張本國，等. 混合基納米流體在汽車散熱器中的穩定性及傳熱特性[J]. 科學技術與工程，2019，19(1)：196-206.

Ding Jie, Wang Ping, Zhang Benguo, et al. Stability and heat transfer characteristics in automotive radiators of mixed?based Nan fluids[J]. Science Technology and Engineering, 2019, 19(1): 196-206. (in Chinese with English abstract)

[25] 沈向陽，李國銘，陳嘉澍，等. Al2O3/丙二醇納米流體的穩定性研究及熱物性測量[J]. 低溫與超導，2021，49(9)：7.

Shen Xiangyang, Li Guoming, Chen Jiashu, et al. Study on stability of Al2O3/propylene glycol nanofluids and its thermo physical property measurement[J]. Cryogenics Refrigeration, 2021, 49(9): 7. (in Chinese with English abstract)

[26] 李興，汪昭瑋，孫一峰. 分散劑對納米流體影響的研究進展[J]. 材料導報，2015，29(23)：6.

Li Xing, Wang Zhaowei, Sun Yifeng. Research of surfactant on the influence of nanofluid. Material Guide, 2015, 29(23): 6. (in Chinese with English abstract)

[27] Guo X, Zou X, Sun M. Optimization of extractionprocess by response surface methodology and preliminary characterization of polysaccharides from Phellinus igniarius[J]. Carbohydrate Polymers, 2010, 80: 344-349.

[28] 鄭丹，王哲，陳占秀，等. 電加熱結構內納米流體穩定性實驗研究[J]. 工程熱物理學報，2021，42(4)：6.

Zheng Dan, Wang Zhe, Chen Zhanxiu, et al. Experimental study on the stability of nanofluid in an electric heating structure[J]. Journal of Engineering Thermophysics, 2021, 42(4): 6. (in Chinese with English abstract)

[29] 鐘桂健，翟玉玲，包桂蓉，等. 納米流體穩定性和粘度的影響因素分析[J]. 材料科學與工程學報，2020，38(1)：8.

Zhong Guijian, Zhai Yuling, Bao Guirong, et al. Analysis of factors influencing stability and viscosity of nanofluids[J]. Journal of Materials Science Engineering, 2020, 38(1): 8. (in Chinese with English abstract)

[30] Afzal A, Khan S A, Ahamed S C. Role of ultrasonication duration and surfactant on characteristics of ZnO and CuO nanofluids[J]. Materials Research Express, 2019, 6(11): 158.

[31] 王宏宇，王助良，杜敏，等. 納米流體的制備及穩定性分析[J]. 河南科技大學學報：自然科學版，2016，37(1)：5.

Wang Hongyu, Wang Zhuliang, Du Min, et al. Preparati on and stability of nanofluids[J]. Journal of Henan Un iversity of Science and Technology Natural Science, 2016, 37(1): 5. (in Chinese with English abstract)

Stability of carbon tube nanofluid based on response surface methodology

Yan Suying1,2, Zhang Tiange1, Yuan Xue1, Gao Hong1, Zhang Huiying1, Zhao Xiaoyan1

(1.,,010051,; 2.,010051,)

Nanofluids can be a new type of heat transfer medium with the high thermal conductivity. Particularly, the traditional heat transfer media cannot fully meet the growing needs of thermal management in the electronic devices in various fields. Among them, the stability is a key factor for the wide application of nanofluids. In order to obtain more stable nanofluids, the dispersants were first screened, and then the stability of the Carbon NanoTube (CNT) nanofluids with the selected dispersant was optimized using the Response Surface Method (RSM). CNT nanofluids were prepared by the two-step method. The comprehensive evaluation index was used to compare the effects of four surfactants on the stability and thermal conductivity of CNT nanofluids. The stability evaluation included the particle size potential and absorbance method. Taking the particle size as the evaluation index, three influencing factors were selected as the mass fraction, ultrasonic oscillation time, and placement of CNT nanofluids. A three-factor and three-level Box-Behnken test was designed to optimize the parameters. The RSM was used to investigate the effects of various factors on the interaction of nanofluid stability. The results show that compared with the rest dispersants, the CNTs nanofluids with the DB dispersant presented the smallest particle size, the highest absorbance, the highest thermal conductivity, and the best comprehensive performance, when the ratio of carbon tube to dispersant was 1:2. Therefore, the DB dispersant was selected to evaluate the performance of CNTs nanofluids. A RSM model was established to accurately describe the particle size of CNT nanofluids using the Box-Behnken experimental design. At the same time, the quadratic polynomial regression equation was obtained for the response value particle size () with the mass fraction of CNT nanofluids (1), ultrasonic oscillation time (2), and storage time (3). The quadratic polynomial mathematical model was established by the experimental data. There was the highly significant (<0.0001) with the correlation coefficient2=0.964 4, indicating an excellent fit between the predicted and the actual value. It infers that there was an excellent consistency between the model and the experimental data. An optimal combination of factors was achieved for the stability of CNT nanofluids using the quadratic regression model, where the mass fraction of CNT nanofluids was 0.27%, the ultrasonic time was 83.45 min, and the standing time was 8 h. In this case, the average particle size was 121.58 nm, and there was a 0.016% error with the predicted value of 120.60 nm. Therefore, this improved model was feasible to optimize the stability of CNT nanofluids. The actual value was close to the predicted value. There was a certain reference value for a theoretical and experimental basis, in order to improve the stability of nanofluids. Response surface test also revealed that the ultrasonic oscillation time and placement time can be selected to improve the stability in the subsequent preparation of nanofluids.

nanofluid; stability; thermal conductivity; dispersant; response surface methodology

10.11975/j.issn.1002-6819.2022.21.030

TK

A

1002-6819(2022)-21-0261-07

閆素英，張田歌，袁雪，等. 基于響應面法的碳管納米流體穩定性[J]. 農業工程學報，2022，38(21)：261-267.doi：10.11975/j.issn.1002-6819.2022.21.030 http://www.tcsae.org

Yan Suying, Zhang Tiange, Yuan Xue, et al. Stability of carbon tube nanofluid based on response surface methodology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(21): 261-267. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.21.030 http://www.tcsae.org

2022-07-28

2022-09-03

國家自然科學基金資助項目（No.51766012）；內蒙古科技重大專項（No.2020ZD0017)

閆素英，博士，教授，研究方向為新能源中的工程熱物理方面。Email：yansy@imut.edu.cn